高校后勤管理中的风险问题研究

赵 兵，赵润恺

(1.西南民族大学，四川 成都 610041；2.中央财经大学，北京 昌平 102206)

高校后勤管理中的风险问题研究

赵 兵1，赵润恺2

(1.西南民族大学，四川 成都 610041；2.中央财经大学，北京 昌平 102206)

在现阶段高校基础设施逐渐完善的背景下，后勤管理中由于其外包或物业管理的特殊性而成为了人们相关研究的焦点，尤其是食堂整体建设与承包的风险也因为承担主体多样而难以分辨，并且定量衡量风险的承担方以及承担方各自负有的风险责任也一直是一个难题.本文针对食堂风险的特殊性，将风险划分为不同的一级、二级类别，区分出五个特定风险承担主体.通过对不同数据以不同方法定量获取，得到各自范畴下的风险指标值作为我们的数据基础，而后将目标规划与熵权法相结合，以特定食堂为例提供给了一种研究食堂风险的可参考方法，并且将两者之间的结果做了相关比较，以期得出有相关性和普适性的建议.

后勤管理；风险管理；风险分类；风险属性值；目标规划；熵权法

1 研究背景与主要内容

本文主要针对高校后勤管理中食堂建设与承包风险及风险分配考虑了一个较为简单的分配方法，结合所利用数据，通过熵权法和两种不同方向的目标规划法进行了初步求解，以期获得相关结论.

在数据方面:首先我们决定出食堂建设和承包的风险的相应风险承担方，然后通过对风险进行一次分类，确定各个风险指标主体集U1-U5，再对于每一特定风险，分别基于5种不同的风险承担主体进行更细的划分，得到风险主体集下的二次划分风险集，对于每一个二次划分的风险集，运用德尔斐调查法和专家法再加上自己的经验，结合层次分析法中的单要素模糊综合模型，我们便可加总二次划分风险集的数值信息，获得每一风险主体初始的风险承担能力的分数预估值，这样我们便得到了可以被加工进行计算的初始矩阵.

在随后的数据运用方面，我们首先通过熵权法，按贴近度大小来确定得到一组风险承担的顺序；然后利用我们课堂所学的目标规划，通过以往风险承担主体实例的相应比例得到各个主体承担风险的先验期望率，并使主观的先验期望率概率与实际测算概率之差最小化而得到一个合理的风险加权数，根据此风险加权数与对应的风险承受能力加权求和便可得到综合评判分数，根据其高低我们也可以确定风险承担方的顺序；最后我们通过带有区间的目标规划来进行计算，并且将三者的结果进行比照和分析，以期得出一定结论.

2 模型假定

1)食堂承包商、食堂承建商、学校、金融机构、投资者分别为五个不同且存在的主体，并且相互之间没有依存关系.

2)风险仅限于我们所归类的风险，并且每一风险都可通过德尔斐法和层次分析法的结合加以量化

3)食堂可以外包，并且独立，并不是由学校的物业公司等统一管理.

4)目标规划的决策矩阵可以由熵权法中的风险属性值矩阵代替，并且量纲方面可以合理吻合.

5)所考虑的风险之间相互独立，没有相关性等，可以单独作为主体承受风险能力的合理量化指标.

3 数据基础

3.1 风险主体的确定

在这一部分中，我们首先针对高校的食堂建设和承包运营划分出不同的风险主题，经过筛选和整理，主要的风险主体有如下:

3.1.1 学校

学校即是食堂建造的地方，由于学校内部较为完善等，我们可以更抽象地把学校视如与政府相似的职能主体.总体看来学校可以决定食堂承包商、建设商和投资者，在其中的谈判和签订过程中也占据着主导地位，并且他们在全过程中可以监督和管理其余主体，进行支持或行为限制.学校同时也是高校食堂建设和承包运营的一个主要风险承担主体，在食堂的建设和运营当中，一般的违约或是损伤等都会承担相应的责任，例如在食物中毒或是食堂内部的人员受伤等.所以学校当然是一个主要的风险承担主体.

3.1.2 食堂承建商

在食堂的建设和承包运营这一流程当中，首先发挥其作用的便是食堂建设商，他们负责食堂的建设和工期的安排，通过设计、采购、施工等工作来确保项目能在合理的时间内保质保量完成.他们在项目建设的过程当中是风险的主要承担人，例如要承担技术风险，完工风险等等.所以食堂承建商也是一个主要的风险承担主体.

3.1.3 食堂承包商

食堂承包商负责对于食堂内部运营的连续性和稳定性做出保障，在食堂修建竣工后，通过与学校签订合同，负责对食堂进行经营和维护，并且可以通过学生在此进行的消费而获取盈利，在承包运营过程当中，其会面对政策和法律法规变化的风险，还有管理机制、技术不断更新等的影响，除此之外也有食堂更换承包商的风险.所以，食堂承包商也是风险的主要承担方之一.

3.1.4 金融机构

由于建设食堂的规模巨大，除了部分私营承包的食堂有股东入股部分和私营投资者的投资部分外，还有一部分是金融机构的贷款，并且期限较长.由于贷款数额巨大和时长的限制，金融机构不免会面对相关的经济风险和信用风险，所以金融机构也是食堂承建和承包运营的主要风险承担方之一.

3.1.5 投资者

很多食堂都由大的私营企业或者投资公司进行了投资并成为股东，除此之外，也有私人注资的行为只不过占比很少.在食堂建设和承包运营过程当中，投资者能够作为股东获取相应利润，同理，他们也应是食堂建设和承包中的风险承担方.

3.2 风险分类

风险表示为损失的不确定性，对于风险，我们的分类方法很多很多，这里不一一列举，最常见分类则是将风险分类为系统风险和非系统风险[1].经归纳总结，与建设和承包经营相关的风险主要有以下几种:系统风险为政治风险、经济风险、法律风险和不可抗力风险；

非系统风险为信用风险、建造风险、运营风险、管理风险，市场风险及环境保护风险.经过筛选，在此处我们的五个主体都会承担并且占比较大的主要有政治风险、经济风险、法律风险、信用风险.而除此之外，每个主体的风险都有较大差异，如食堂承建商所要面临的完工风险和投资者的利益风险就不属于任一其他主体所含有的风险范畴，所以我们将每一主体中没有被五个主体含有的风险归类为特有风险(特有风险中可能会有两个主体共同含有的，例如学校和承建商都会承担工期风险).

经过上述分类，我们已经将风险的一类分级得到，即政治、经济、法律、信用和特有风险，而二级风险则需针对不同主体来进行获取，经过分析和斟酌我们得出风险集[2].

3.3 风险属性值矩阵

1)无量纲化处理及相关性分析

指标体系中所含的各指标类型不尽相同，且具有不同的量纲，因此，需将这些指标无量纲化，再进行在综合评价.对每个变量(指标)的数据分别相关性分析，计算指标间的pearson相关系数，得出相关系数矩阵，类间相近性度量的计算选用类平均法.通过计算每个指标见的pearson相关系数，可以得知该指标体系已经包含了主要的风险因素，并且指标间信息重叠较少，能够很好的用以综合评价.

五个风险指标相关系数矩阵

表1 相关系数矩阵Table 1 The matrix of correlation coefficient

2)对定性数据的处理

如上所述，在面对可以用数据进行准确衡量的风险指标值时，我们可以采用模糊数学的方法得到准确的评价分数，然而在面对一些主观因素较重或者无法用数据进行衡量的指标属性值时，我们则采用贝叶斯估计法[3]来获取我们需要的信息，贝叶斯定理可以为主体利用搜集到的有效信息来对原有判断进行修正，通过此我们可以很好地刻画我们的决策准则，具体如下:

当我们面临一个选择时，如果我们已经有了一个价值的概念，那么贝叶斯定理可以给我们提供一种方法来进行比较从而决定哪种选择更好，我们令u为效用函数，它给一个行动每一个结果都能指派一个数值，来反应结果的好坏程度.所以，当我们说决策A优于B时，我们则有如下的式子进行表示:

其中，pi是行动Ai可能导致的结果的概率，而ui是那些结果的效用，所以其也叫做行动Ai的期望效用.在效用是正效应的情况下，我们总是选择期望效用最大的一条路径，这也便成为EU最大化.

在我们所处理的风险承担的具体问题中，针对每一主体下特殊的无法用数据衡量的具体指标值，我们可以采用上述方法来获得初始指标值.然而，此种方法由于对于不同的属性值可能会采用不同量纲，所以我们需要进行无量纲化，即针对纵向数据列的每一个数据除以max值即可，这样得到一个无量纲化值之后，乘上我们初始的预期目标值90便可以得到相应风险承受能力的准确数值.重复此方法我们便可以得到第一层级指标中无法用数据衡量的部分，结合已用数据衡量完成并且可以具体赋值的其他第一层级指标值，我们可以通过模糊数学的方法将其加权累和，得到各个主体信用风险类的具体风险属性值:

具体操作我们以各个主体的信用风险为例，如下:

结合我们获取数据中的坏账比例，我们可以得到学校的与坏账相关的矩阵:

表2 坏账分类Table 2 The table of the classification of bad debt

而根据贝叶斯的先验，我们先假设采取两种方法的概率为相等的0.5，根据所得数据我们可以得到，这样所得到的坏账数/应收账款总数为:24338/3，403，000.00＝0.007152，由于这个是负向指标，即比值越小其风险承受能力越强，所以我们取倒数并且再除以一百，得到其正向修正后的指标值为1.39821同理，我们可以得到其他四个主体的比例分别为0.792319，1.211782，0.652498，0.994282，我们取最大max为1.39821，将每一主体的值分别与其作比在乘上90，取整后即得信用风险行无量纲化后的取值为:51，78，42，72，64.这也便是我们得到的初始矩阵中第五列的值.

3)对其它数据的处理

对于其他数据的属性值，我们采用层次分析法中的模糊综合评价法[4]和德尔斐专家法相结合来进行获得.

我们运用德尔斐法和经验分析法得到人们对于风险承担方的一个主观偏好值，由于我们有5个不同的风险承担主体，所以向量p共有5个分量.针对某一特定承担主体，我们有属于其本身的风险属性，而风险属性，如上图所示，已经被我们进行了较细的分类，而使用相同的分类范畴也保证了我们可以进行横向比较以及目标规划的决策可操作性.

对于风险承担主体xi，我们分别从政治、经济、法律及特有风险四个方面来进行考量，这也便是我们的属性集U，针对每一属性Ui，我们再其下进行更细的划分，例如学校的政治风险U1我们可以分为U11(因食堂政策改变导致的法律不可抗力)，U12(学校相关人员腐败)两个方面.为了得出我们针对每一特定主体的第一属性集，我们采用一种层次分析法——模糊综合评价法来将第二层属性集的因素进行加总，例如投资者的法律风险U3下有与学校主体发生诉讼和法庭仲裁风险U31，法律变动风险U32，相关人员法律及道德素质U33，内控制度的完善和执行U34四个细化的指标因子，针对这四个指标因子，我们通过所得数据和预期值之间的差异以及专家德尔斐等方法得出评价要素权重隶属子集A＝{a1，a2，a3，a4}后，通过前期的数据获得我们得到企业分别在各个方面获得的分数B＝{b1，b2，b3，b4}，再以C＝A×BT即可得到法律风险U3这一指标所得到的风险值(我们假设风险值越高越好，以后所见也如此理解，若不是正向指标，我们会在之后的目标规划板块进行处理)，并使d32等于C值，这样我们可以通过对5个主体的分别4个指标进行量化而得到一个矩阵，将其与先前所得数据进行综合后得到如下矩阵(横向量分别代表学校，投资者，金融机构，食堂承建商，食堂承包商这五个风险承担主体，列向量分别为政治风险，经济风险，法律风险，信用风险，特有风险).

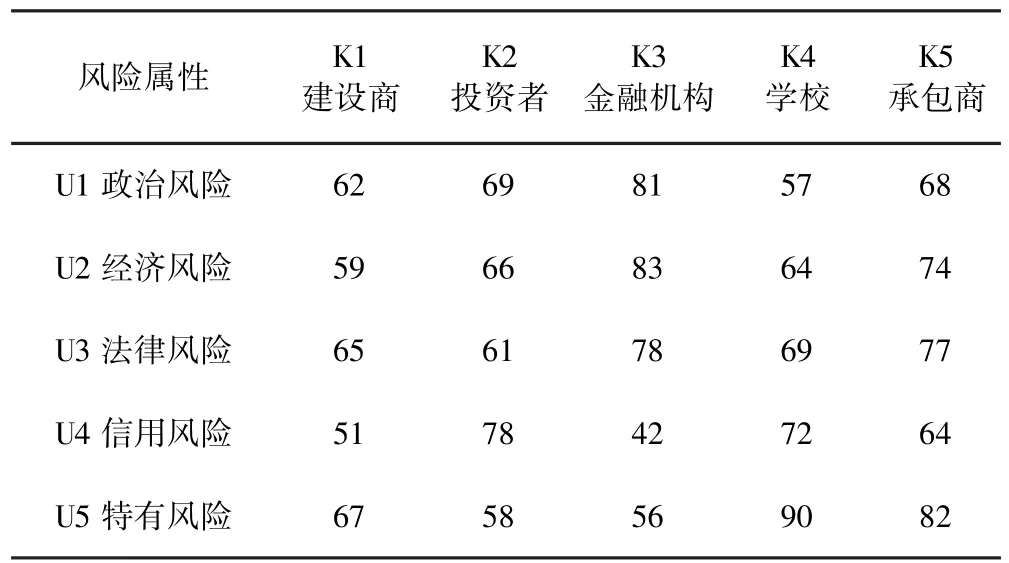
表3 风险属性值Table 3 The statistical table about risk value

4 熵权法运用

简而言之，此方法是通过信息熵的值获得对原矩阵属性指标的加权向量，而后通过其与目标值的欧式距离来进行判断，距离越小(离指标值贴进度越高)即离理想值越近则越优[5-6]，具体步骤如下:

由上，我们得出初始矩阵如下图(为了在excel中进行计算和后续距离和熵权的计算方便，在此对矩阵进行了转置，即此时列向量分别代表五种不同风险，行向量分别对应五个不同主题):相对，我们的目标矩阵取预期值都为90.

首先，我们根据我们的目标差值率(即以每一列与预期值90相减再除以90的比率值为5∗5矩阵中列向量的值)，我们可以得到无量纲规范化矩阵，

对于五个不同主体的最优与最劣评价，我们可以得到:

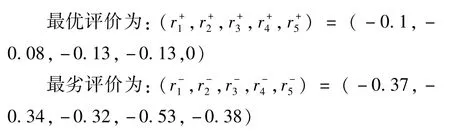
在利用熵权法计算指标权重之前，我们对矩阵D进行初始化处理，得出标准化矩阵为将上述矩阵代入得到各个指标的概率矩阵Z为:

所以可以得到M1＝1.790088，M2＝0.827852，M3＝2.10882，M4＝0.011341，M5＝0.200633

由于M值越低承担风险的综合能力越高，所以很明显地看出承担风险的顺序次位应为K4学校，K5食堂承包商，K2投资者，K1食堂建设商，K3金融机构.

5 目标规划

在这里我们采用多属性决策中的目标规划[7]，具体内容如下:

设X＝{x1，x2，…xn}为决策问题的方案集合，U为属性集，W为权重向量，而决策者对选择xi为风险承担者有主观偏好pi，我们按第i个属性ui进行测度，即可得到aij从而构成决策矩阵A.在这里，我们可以将方案集合看作风险承担方主体集合，属性集看作风险的不同属性分类构成的集合，测度值视为相应主体承担相应风险的能力，则可以将前面所得到的风险属性值矩阵直接视为此处的决策矩阵.

为了判断和对比不同主体所应承担的风险数量，我们需消除不同物理量纲的影响，即将决策矩阵进行规范化处理，而处理后的矩阵我们可以得到针对于每一风险承担主体的综合风险承受能力与权重的关系为:

当wi值确定时，综合属性值越大则该主体承担越优，所以zi可以直接作为客观偏好值，但是由于决策者经常会对承担主体的选择有偏好pi，所以若要将客观和主观向结合，我们最优的权数是当偏好值与综合风险承受能力最近之时(相同量纲情形下)，用公式表示如下:

且正负偏差都大于或等于0.

结合如上所示，我们可以建立目标规划模型如下:

结合通过上述方法求得的w∗，我们可以得到主体xi的综合属性值为:

具体求解过程如下:

首先，在前述的数据应用与模型代入中，我们将属性都视为正向属性(负向可去倒或取负再规范化即可)，五种风险也都是如此，即分数越高，抵抗风险的能力和风险应对得分较高.

对五个风险，我们通过德尔斐专家法可以得到一个权数的范围，即针对五个主题都可通过一组相应的权数来得到合理的分数.我们结合前面所得数据和德尔斐法给出权重的范围:

对于五个风险主体而言，我们根据经验调查法以及对实际案例的考察(通过将问题交予专家让其根据经验给不同的合理的p值)可得投资者对五个主体K1-K5分别的主观偏好值可以取为:

我们利用和上述的熵权法相同的处理数据方法，先将矩阵A规范化:

由于都是正向数据，所以:

根据已经有的信息，我们可以有下列目标规划模型:

求解:

excel:通过EXCEL中目标线性规划[8-9]，我们可以得到权重向量[10]为w1-w5分别为0.1，0.1543，0.15，0.2，0.3957

在目标规划中，我们通过对综合属性值排序可以得到优先顺序为K5食堂承包商，K4学校，K2投资者，K1食堂建设商，K3金融机构.

6 带区间的目标规划

在上述目标规划方法当中，由于我们通过区间值进行目标规划求出了确定值，这种方法虽然能较准确得对不同承担主体来进行比较，然而偶然性和不确定性也较大.另一种合适的方法是进行带有区间的目标规划[11-12]，通过此方法我们可以合理运用开始所得到的关于决策W权重值的所有信息(有点类似于置信区间的概念).

为了运用带有区间的目标规划，我们对规范化后的矩阵进行了一个上下百分之十的区间拓宽，即决策相关的规范化矩阵可以变为一个5∗10矩阵如下图(其中相邻两列为某一值的上下分别乘1.1和0.9的值)，我们可以得到目标规划方程如下:

由于我们希望目标值在预期值的上下两范围之间，所以取p2为2倍p1的任意值，为方便起见，我们取前者为2，后者为1.

1)excel:通过EXCEL中目标线性规划我们可以得到结果如下:

排序的结果也为K4学校，K5食堂承包商，K2投资者，K1食堂建设商，K3金融机构.

并且我们可求得相应五个承担主体的风险承担能力所在区间分别为[0.6811，0.8313]，[0.7024，0.8580]，[0.6634，0.8109]，[0.8118，0.9932]，[0.8054，0.9824].

易见，排序结果与熵权法所得值相同.

7 结论对比及分析

本文在对食堂风险[13]进行理论分析的基础上，构建基于目标规划和熵权法的方法，利用食堂建设、承包及运营项目期间风险属性值的数据等，对不同风险相应的承担主体进行实证研究，得到以下结论:

1)模型对比

在带区间的目标规划中，我们可以看到其所得方案排序与用熵值法一致.相较而言，熵权法是用欧式距离计算实际值与目标值之间的差距而取最小值即最优方案；而目标规划则利用了主观性较强的pi一值，这在一定程度上会对原结果造成影响，不过两种方法各有其优越性.前者是从客观角度纯粹从数学的距离性上进行分析，按照风险应对能力强弱来进行排序；而后者则考虑了人为的主观因素，在其中添加了人的偏好变量，可以包含更多的因素.我们可以看到两种方法在结果上是大致相同的，只有一二位的风险承担主体稍有差异.

而第三种带区间的目标规划虽然只是在决策矩阵中上下增减了百分之十，但是却有效地利用了其中所有的信息，在建立方程时与前面的目标规划虽然大同小异，但是所得结果却是不同的，并且每个承担主体既能给出区间值又能给出一个准确的中心值，可以说是一个简单易懂但却行之有效的评判方法.

2)相关建议

由于食堂建设项目是一个特许协议，所以政策风险[14]是首先应当防范的，并且基于我们所得出的结论，其主要是由学校进行绝大部分的担负职能.所以为了保证食堂运营期间的长期稳定，学校的话语显得至关重要.由于在协议中明确了学校部门必须承担的义务和与其控制力相匹配的风险，并提供一定的政策保证.如果合作主体之间相抵触，或者在投资回报率满足不了私营机构或个人投资者对利润的要求时，学校应适当的提供进一步政策支持和相应的措施以保证食堂建设及运营等的可行性，所以学校在食堂的各个流程中做出相关决定等时需要格外的谨慎.

在风险承担[15]方面，金融机构的风险承担属性值远小于其他四者，所以在考虑风险时可以对其赋予相对较少的重视.这也是由于由于投资总额中来自与金融机构的部分与投资者的部分相比会少很多，所以在项目资本和其他等方面将我们考虑的范围缩得更小一点并且更有针对性地提出应对方法和改善措施.

投资人和承建商及运营商作为三个承担属性值相近的主体，其对食堂承建项目风险影响大小也相对接近.承建商的风险全来自于第一阶段，所以可以考虑为先决风险，在项目运营时期可以不用将此主体划在考虑范畴.

[1]向文武，亓霞，郑镭.浅谈项目融资与风险度量[J].金融证券.学术理论，2003，2:27-29.

[2]柯永建.中国PPP项目风险公平分担[D].北京:清华大学，2010: 57-60.

[3]任晓明，李章吕.贝叶斯决策理论的发展概况和研究动态[J].科学技术哲学研究，2013，4:3-5.

[4]马文彬.校园环境质量的模糊综合评价方法[D].四川雅安:四川农业大学，2004，6:2-5.

[5]郭显光.熵值法及其在综合评价中的应用[J].财贸研究，1994，6: 56-60.

[6]陈汉军，杨雪.欧几里得距离的几种定义与应用[J].天津轻工业学院学报，2003，1:21-23.

[7]徐泽水，张文献.多属性决策中的目标规划[J].应用数学与计算数学学报，2001，12:46-48.

[8]孙爱萍，王瑞梅.如何利用excel求解线性规划问题及其灵敏度分析[J].办公自动化，2009，5:22-15.

[9]罗罡辉，叶艳妹.多目标规划的LINGO求解方法[J].计算机应用与软件，2004，2:5-6.

[10]徐蔼婷.德尔菲法的应用及其难点[J].中国统计，2006，9:6-7.

[11]王鹏飞，李畅.不确定多属性决策双目标组合赋权模型研究[J].中国管理科学，2012，8:105-108.

[12]胡宝清.区间目标规划与模糊目标规划[N].全国模糊系统与模糊数学学术年会，2004，7:5-10.

[13]邓瑞.浅析中国高校食堂外包中的风险管理[J].经济研究导刊，2013，33(8):277-279.

[14]谢志平.公共政策风险及其防范[J].东北财经大学学报，2009，4:2-3.

[15]解维敏，唐清泉.公司治理与风险承担——来自中国上市公司的经验证据[J].财经问题研究，2013，1:6-7.

(责任编辑:罗敏，付强，李建忠，张阳；英文编辑:周序林)

Risk problem research for logistic management in colleges and universities

ZHAO Bing1，ZHAO Run-kai2
(1.Southwest University for Nationalities，Chengdu610041，P.R.C.；
2.Central University of Finance and Economics，Beijing102206，P.R.C.)

Nowadays，as the infrastructure in school is ameliorated，canteen，owing to the specialty of its ownership and management，becomes the focus of research.The risk of the canteen remains hard to distinguish.Moreover，it is a troublesome issue to measure the responsibility of the risk-taking subject in a quantitative way.This paper aims at the specialty of the risk of canteen.the risk is divided into two levels and five subjects are recognized as the risk-taking ones.Based on the value of weighing the risk，the goal model and the entropy method are used to give a quantitative rank of the risk-taking subjects from the high risk to the low rick.Then these two approaches are compared and some relative suggestions are given.

logistic management；risk management；risk classification；risk index；goal model；entropy method

F22；G647.6

A

2095-4271(2015)04-0512-08

10.11920/xnmdzk.2015.04.023

2014-12-10

赵兵(1965-)，男，汉族，四川西充人，教授，博士，硕士生导师，研究方向:城乡规划与生态规划.E-mail:190288595＠qq.com；赵润恺(1994-)，男，汉族，四川成都人，中央财经大学统计学院2012级金融数学专业学生，研究方向统计与数学(金融数学)以及项目融资管理；E-mail:191574225＠qq.com.

国家社科基金项目(项目编号09XMZ041)；四川省科技厅科技支撑项目(2012SZ0053)