＊基于盒维数的锚杆工作荷载无损检测研究

梁腾飞，冯剑锋，卞德存，闫 东，李 义（太原理工大学矿业工程学院，太原030024）



＊基于盒维数的锚杆工作荷载无损检测研究

梁腾飞，冯剑锋，卞德存，闫 东，李 义
（太原理工大学矿业工程学院，太原030024）

摘 要：为研究锚杆工作荷载，应用了分形理论中的盒维数方法。根据一维杆波动理论，在锚杆外露端头安装一个自激式加速度传感器，利用锚杆无损检测加载试验台分级加载、检测标定测得锚杆－围岩相互作用体系在激发荷载作用下的速度响应，计算其加速度响应曲线的盒维数，拟合得出荷载－盒维数曲线，直观地判断锚杆工作荷载和锚固质量。

关键词：锚杆；工作荷载；盒维数；响应曲线

（E－mail）tengfeiliang16＠163．com

通讯联系人：赵金昌（1974－），男，副教授，硕导，（Tel）13834155285

随着我国大规模岩土工程的蓬勃发展，锚杆锚固技术在地下支护工程、边坡稳定工程和结构抗震、抗浮、抗倾覆等工程领域得到了全面的推广与应用。自19世纪80年代以来，众多学者对锚杆锚固质量的无损检测进行了大量的研究，但由于存在底端反射识别困难，反射时间无法准确确定等问题，对锚杆的工作载荷和锚固质量均没有给出比较精确、简便的测定办法［1－6］。

分维是分形理论中的一个基本量，是用来表明分形体填满嵌入欧几里德空间的程度，它可以定量的描述分形体的复杂性。分形几何中用于计算分形维数的方法有很多，如信息维、关联维、相似维、盒计数维等。对于不同的研究对象，相应的有各自适用的维数定义。在求解分形维数的众多方法中，盒维数的数学计算以及经验估计相对容易，因此是应用最广泛的维数之一。分形体的盒维数数值体现的是对于该对象的统计自相似性，也就是分形。随着理论研究的不断深入，分形理论主要应用于岩石力学、爆炸力学以及地震学等方面［7－8］。

随着对锚杆荷载研究的深入，发现在一定的试验条件下，确定采样长度和采样频率，重复的进行锚杆实时荷载试验所获得的振动信号波形满足统计自相似性随机分形特征［9－12］，也属于岩石力学的应用范畴，符合盒维数的应用前提。因此本文根据分形盒维数理论，建立模型，得出振动加速度响应曲线的分形盒维数，建立了盒维数值与锚杆实时工作荷载的关系，从而得到了一种全新的实时判断锚杆工作荷载无损检测方法。该方法可以直观的对锚杆工作荷载和锚固质量进行判断。

1　盒维数理论和模型

1．1 理论基础

假设锚杆受激振动产生的波信号s∈F，F是n维欧式空间Rn上面的封闭的集合。将Rn划分成尽可能小的宽度为δ的正方形方格，如果Nδ是网格宽度为δ的离散空间上覆盖F集合最少的网格个数，那我们将振动波s盒维数定义为［13］

在我们实际试验测试中，每个采样时间间隔Δt内，波形曲线是一段直线。因此我们在用基本尺寸为δ的方形网格覆盖集合F的时候，δ的最小值应该大于Δt。在实际计算中，我们会根据振动波信号曲线，得出曲线被方形网格覆盖的最小尺寸k1δ和最大尺寸k2δ，然后将一系列尺寸为kδ（k1≤k≤k2）的方形网格对振动波信号曲线进行分割、覆盖，得到每个不同尺度下的网格有效覆盖数量Nkδ，然后通过最小二乘法得到了－lg（kδ）－lg（Nkδ）的拟合直线，该直线的斜率就是该波动信号曲线的分形盒维

数D［14］。

因为在锚杆锚固共同工作的时候，锚杆实际的振动是非常复杂的，为了便于实验室研究和计算，在分析锚杆的纵向振动时，我们做出如下假设［15］：

1）锚杆受到激发后的振动应在弹性限度以内，各质点的位移、应力和应变之间的关系满足弹性胡克定律；

2）锚杆材料分布均匀或分段均匀且各向同性；

3）在锚杆受到激发产生振动的时候，其截面保持为一个平面，不会存在相位的差别或者振动的滞后或超前现象。

1．2 盒维数的计算模型

振动产生的加速度响应曲线是一条双向尺度曲线：纵向为振动幅值，横向为时间尺度。因此在对曲线进行盒子覆盖的时候，为了准确地反映曲线的双向尺度特性，本文采用矩形盒模型来计算加速度响应曲线的盒数量。具体办法就是用一个尺度为δ1×δ2的矩形盒子去覆盖F集合，其中δ1为时间尺度，δ2为振幅尺度。其中横向尺度δ1由信号采样的间隔时间Δt决定，纵向尺度δ2由曲线最大峰值所对应的波峰或波谷近似确定。在此无标度区内对应的（－lgkδi，lgNkδi）点数为k2－k1＋1。在用矩形盒覆盖的时候，无标度区内－lgkδi与lgNkδi满足线性回归方程

lgNkδi＝－Dδ1×δ2×lgkδi＋b，i＝1，2．（2）

盒维数值计算式为

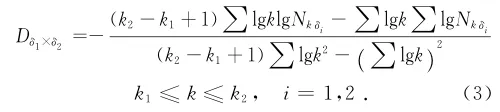
2　锚杆拉拔实验研究

对锚固质量良好的锚杆进行拉拔实验，同时在不同的荷载状态下于锚杆端头激发应力波，将所获得的振动加速度响应曲线进行盒维数计算，最终拟合出荷载－盒维数曲线。

2．1 实验设备

实验设备主要有：SY－40锚杆无损检测加载试验台、KMJ－1型矿用锚杆锚固质量检测仪。该实验测试系统中的射针式传感器以及它与锚杆的连接装置都是自行设计的。将传统的信号激发与接收装置集成为一体，采用弹簧驱动射针的方式激发应力波。该方法可以有效地减弱外界噪音信号干扰，大大提高了测试数据的准确性。锚杆连接设备为面接触的形式，改善了接口与锚杆的耦合效果，同时克服了采集信号质量差的缺点［16］。

2．2 实验试件制作

由于本文目的是研究盒维数与荷载二者之间的关系，因此采用锚杆直径、锚杆长度和锚固长度一样的试件进行研究。锚杆材料为普通建筑圆钢，长度分别为1．6m，直径18mm。为了与岩土工程现场的锚杆接近，用标号为C30的水泥砂浆作为锚固剂，具体配比是水泥：细沙＝1∶2（质量比），水灰比为1∶0．5（质量比）。在内径88mm、外径90mm、长为50cm的钢管正中间安置锚杆后浇筑锚固剂并捣震，然后将试件的锚固段放在水中同步养护，直到28d龄期强度。

每根锚杆制作一个试件，试件的示意图如图1，试件的参数见表1。

图1　试件示意图Fig．1 Specimen schematic

表1　试件参数Table 1 Specimen parameters

试件1是为了观察光杆的盒维数值与荷载的关系，同时与锚固后的锚杆形成对比；试件2和试件3是重复性实验，为了采集更多数据，用以验证结果的准确性。

2．3 实验仪器安装及参数选择

在安装传感器时应该注意以下几个问题［17］：

1）传感器安装完毕后应当与锚杆在同一水平轴线上；

2）传感器与配套螺帽、螺帽与锚杆端头之间要充分耦合，不然会影响加速度传感器，引起寄生振荡等干扰情况；

3）数据采集敲击传感器时动作要干脆利落。

在测试仪器参数的选择时，由于采样率的提高，采集相同长度的信号，测得的信号长度就会增加，仪器存储空间就会增加。因此实验时，在满足采样长度的条件下应当降低采样率。通过多次的实验调试，我们发现采样频率500Hz，采样长度10k为宜。

2．4 实验步骤

试件养护完成后在锚杆拉拔机上进行拉拔实验，步骤如下：

1）安装试件并施加一定的荷载，用小锤敲击锚杆端头的应力波激发装置，通过应力波传播到变阻抗界面时发生反射和透射测得加速度响应曲线；

2）利用拉拔实验机改变试件的荷载，设定间隔加载级别逐级加载，当加载到某一荷载时，保持该荷载持续约120s再进行测试，得到在不同荷载下的加速度响应曲线；

3）将采集的曲线导入Matlab软件，利用盒维数理论以及判定盒维数的程序进行计算，采用最小二乘法，得出拟合直线，计算出盒维数值。

4）用Origin将不同荷载下的盒维数值进行拟合，得出盒维数与锚杆工作荷载的曲线。

3　实验数据整理及分析

3．1 盒维数的计算及荷载－盒维数曲线的拟合

图2为试件2在荷载为5kN的时候－lgkδi与lgNkδi拟合的直线。（在具体进行直线拟合时，采样间隔时间Δt做归一化处理，矩形盒的横向尺度δ1的基本尺寸也取为0．2×10－5，即δ1＝Δt＝0．2× 10－5，最后采用不同的矩形盒对曲线完全覆盖。图2所示拟合后的直线方程为

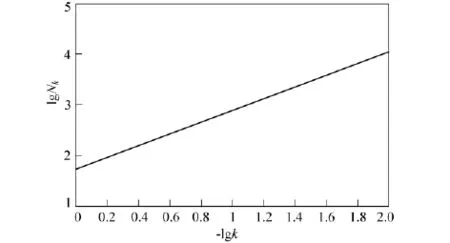
图2　－lgk与lgNk的关系Fig．2 Relationship of－lgkand lgNk

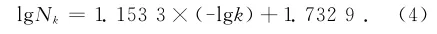
表明试件2在荷载为5kN的时候加速度响应曲线的盒维数数值为1．153 3。

其余的应力波曲线也做同样的处理。最终我们将不同荷载下的盒维数值进行统计，将统计结果导入origin进行拟合，得到了荷载－盒维数曲线。

3．2 盒维数与荷载相关性分析

通过图3可以看出：试件1在73kN的时候锚固失效了，对应的荷载－盒维数曲线在73kN时也达到了峰值点。试件2和试件3都是在42kN的时候锚固失效，对应的荷载－盒维数曲线也都在42kN左右时也达到了峰值点。

通过观察发现，采用盒维数方法得出的荷载－盒维数曲线的最高点与测力－位移曲线的锚固失效点

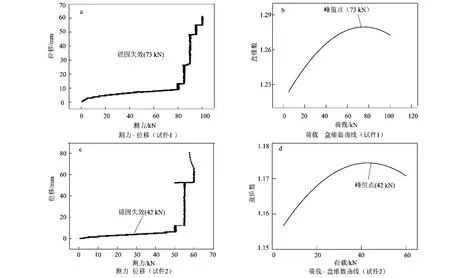
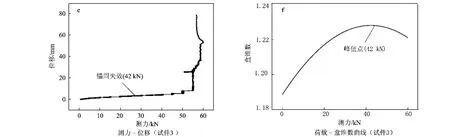
图3　测力－位移曲线与荷载－盒维数曲线的对比Fig．3 Contrast of load－displacement curve and load－box dimension curve

正好对应。这样就可以利用荷载－盒维数曲线很直观地判断锚固试件的荷载情况。当盒维数数值位于最高点值前面的时候，可以认为锚杆还近似处于弹性变形阶段；当盒维数数值与最高点值相等或非常接近时，可以认为锚杆处于锚固失效阶段。

3．3 荷载－盒维数曲线分析

图4为不同试件的荷载－盒维数曲线的对比。试件1在73kN达到了曲线峰值，其余两个试件在42kN达到了曲线峰值。

图4　荷载－盒维数曲线对比Fig．4 Load－box dimension curve contrast

可以得出：

1）不同的试件，拟合出的荷载－盒维数曲线趋势基本一致，先增大，到达峰值后减小；

2）相同锚固参数的试件盒维数数值有差异，但

是达到盒维数最大值的荷载相同。

4　结论

1）通过理论和实验研究，在锚杆无损检测中引入盒维数模型是可行的，是锚杆锚固质量无损检测的一种直观、简便的评价方法。

2）建立锚杆荷载与加速度响应曲线的盒维数模型充分考虑了振动波时间和幅值的双尺度效应。基于该模型计算振动波盒维数更准确，具有说服力。

3）通过盒维数曲线，可以直观判断锚杆的锚固质量：当盒维数数值位于最高点值前面的时候，可以认为锚杆还近似处于弹性变形阶段；当盒维数数值与最高点值相等或者非常接近的时候，可以认为锚杆处于锚固失效阶段。

5　讨论

试件2与试件3实验参数完全一致，得出的荷载－盒维数曲线趋势基本一致，但是盒维数数值大小却存在差异，初步推断是因为端头激发不稳定以及数据采样长度造成的。本文建立了荷载、盒维数二者之间的基本关系，是一个初探性研究，具体的不同长度、不同直径以及不同锚固长度下荷载与盒维数的关系今后再做进一步研究。

参考文献：

［1］ 田凯．岩土工程锚杆检测技术发展现状［J］．施工技术，2007（11）：354－357．

［2］ 汪明武，王鹤龄．锚固质量的无损检测技术［J］．岩石力学与工程学报，2002，21（1）：126－129．

［3］ 许明，张永兴．锚固系统质量检测的小波分析法［J］．岩土力学，2003，34（2）：262－265．

［4］ 李维树，甘国权，朱容国，等．工程锚杆注浆质量无损检测技术研究与应用［J］．岩土力学，2003，24（SI）：189－194．

［5］ Beard M D，Lowe M J S．Non－destructive testing of rock bolts using guided ultrasonic waves［J］．International Journal of Rock Mechanics and Mining Sciences，2003，40（4）：527－536．

［6］ 李义，刘海峰，王富春．锚杆锚固状态参数无损检测及其应用［J］．岩石力学与工程学报，2004，23（10）：1741－1744．

［7］ 张济忠．分形［M］．北京：清华大学出版社，1995．

［8］ 谢和平，张永平，宋晓秋．分形几何———数学基础与应用［M］．重庆：重庆大学出版社，1991：37－42．

［9］ Gregogy W W，Oppenhein A V．Estimation of fractal signals from noisy measurements using wavelets［J］．IEEE Transaction on signal processiong，1992，40（3）：611－623．

［10］ Maragos P，Sun F K．Measuring the fractal dimension of signals：morphological covers and iterative optimization［J］．IEEE Transaction on signal processiong，1993，41（1）：108－121．

［11］ 娄建武，龙源，方向．基于反应谱分析的爆破震动破坏评估研究［J］．爆炸与冲击，2003，23（1）：41－46．

［12］ Yuen S Y，Fong C K．Fractal dimension estimation and noise filtering using Hough transforms［J］．Signal Processing，2004，29（4）：907－917．

［13］ 娄建武，龙源，徐全军，等．爆破地震信号的分形盒维数数值分析［J］．爆炸与冲击，2004，（24）：363－364．

［14］ Tadolini S C．Evaluation of u ltrason ic measurement system for bolt load detem inations［R］．The U S Bureau of Mines，Denver，CO，1990．

［15］ 刘海峰，李义．应力波反射法锚杆底端反射显现规律的实验研究［J］．太原理工大学学报，2000，31（4）：440－443．

［16］ 李义，王成．应力反射波法检测锚杆锚固质量的实验研究［J］．煤炭学报，2000，25（2）：160－164．

［17］ 任智敏，李义．基于声波测试的锚杆锚固质量检测信号分析与评价系统实现［J］．煤炭学报，2011，（36）：192－193．

（编辑：贾丽红）

Nondestructive Testing of Bolt Working Load Based on Box Dimension

LIANG Tengfei，FENG Jianfeng，BIAN Decun，YAN Dong，LI Yi
（College of Mining Engineering，Taiyuan University of Technology，Taiyuan030024，China）

Abstract：Box dimension method in fractal theory was used to study the working load of bolts．According to the wave theory of one dimensional bar，a self oscillating acceleration sensor was mounted on the exposed end of the bolt．Nondestructive testing of the bolt，step loading of test beds，and calibration were used to measure speed response of interaction system of bolt－surrounding rock under excitation loads，to calculate the box dimension of acceleration response curve．By the fitted curve of load－box dimensions，anchor bolt working load and anchor quality could be visually determined．

Key words：bolt；working load；box dimension；response curve

作者简介：梁腾飞（1988－），男，山西太原人，硕士生，主要从事结构无损检测方面的学习与研究，（Tel）15340707575，

基金项目：教育部博士点基金资助项目：群锚结构锚杆荷载演化与围岩稳定性预测机理研究（20111402110003）

收稿日期：＊2014－10－25

文章编号：1007－9432（2015）03－0327－05

DOI：10．16355／j．cnki．issn1007－9432tyut．2015．03．016

文献标识码：A

中图分类号：TD353．6