轮胎激光散斑干涉相位图多方向频域滤波方法
2015-12-17陈冬雪刘桂雄彭艳华曾启林
陈冬雪,刘桂雄,彭艳华,钟 浩,曾启林
(1.华南理工大学机械与汽车工程学院,广东 广州 510640;2.广州华工百川科技有限公司,广东 广州 510640)
0 引 言
激光数字剪切散斑轮胎无损检测技术具有实时、全场非接触、无损、结构简单、无需防震装置等特点,已经成功应用于轮胎生产缺陷探测上。通过时间相移技术生成的包裹相位图含有大量噪声,严重影响包裹相位图解包,难以实现对轮胎缺陷尺寸精密测量,故必须对生成包裹相位图进行图像滤波处理,最大程度地消除噪声并尽可能地保留包裹相位图的细节信息。中值滤波[1]对脉冲干扰、椒盐噪声具有很好的抑制作用,但不适用于线、尖顶等细节较多图像[2];频域低通滤波能够有效抑制散斑噪声,但又容易去除图像边缘信息[3];Qian K M[4]研究一种二维加窗傅里叶变换滤波方法,取得较好滤波效果,但算法复杂,滤波过程需设置多达9个参数。LI C C等[5]提出一种局域傅里叶变换滤波法,通过对图像局域(非全局)进行傅里叶变换,具有较好图像细节保持能力,但滤波质量与选取窗口大小有关。王永红等[6]提出一种条纹正余弦分解、频域低通滤波相结合滤波方法,该方法能够在保留图像边缘信息基础上,较好地滤除图像中的散斑噪声且算法简单、计算速度快,只需一次滤波,但当干涉条纹比较密集时,存在噪声抑制、保留条纹边缘细节的矛盾。本文通过分析轮胎缺陷剪切散斑干涉相位图的形成及其条纹特征,并根据其条纹密度分布特点,提出研究一种多方向频域低通滤波方法。
1 轮胎剪切散斑干涉相位图条纹特征
首先对含有缺陷的轮胎进行真空加载,然后通过激光散斑轮胎无损检测装置获得轮胎变形前、后的散斑图,最后对轮胎变形前后散斑图进行相减处理,并经过相移算法就可得到轮胎缺陷包裹相位图,其相位条纹是离面位移在错位方向一阶导数的等直线条纹[7]。图1为错位散斑干涉条纹示意图,图2为轮胎缺陷包裹相位图。可以看出,轮胎缺陷包裹相位图是典型“蝴蝶状”条纹图,错位方向条纹密度比其法向条纹密度要高。
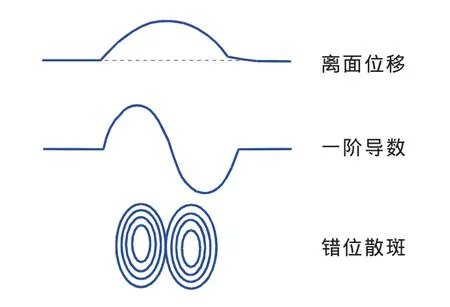
图1 错位散斑干涉条纹示意图
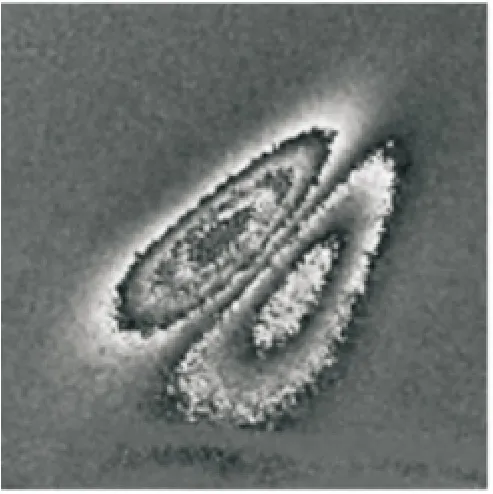
图2 轮胎缺陷包裹相位图
条纹密度越高,条纹间距就越小,条纹梯度变化就越大,条纹空间频率也越大。由于轮胎缺陷包裹相位条纹图在错位方向的条纹密度比其法向的条纹密度要高,故在对轮胎缺陷包裹相位条纹图进行频域低通滤波时,可根据不同方向的条纹密度来设置不同的截止频率,这样可以达到更好的滤波效果。
2 多方向频域滤波理论分析
2.1 一维频域低通滤波
时域信号通过傅里叶变换就可转换为频域信号,图像大部分能量处于频谱的低频部分,图像细节、噪声处于频谱的高频部分。将频谱通过低通滤波器处理,就可将高频信号滤除,再经过傅里叶反变换就可得到滤波后的图像。设f(x)为一维离散函数(x=0,1,2,…,N-1),F(u) 为其傅里叶变换函数(u=0,1,2,…,N-1),则其傅里叶变换及其傅里叶反变换公式分别为
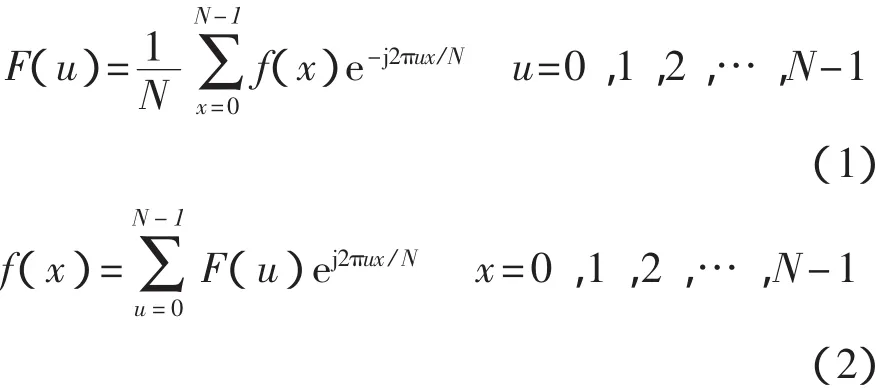
常用低通滤波器有巴特沃斯滤波器[8]、一维低通滤波器、二维低通滤波器等,本文选用一维理想低通滤波器,在滤波之前将傅里叶变换的原点移动到频率坐标下中心处。设D(u)为频域坐标下任一点到中心点距离,截止频率为D0,滤波系数为H(u),则其传递函数为
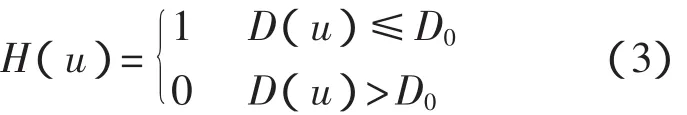
2.2 多方向频域滤波
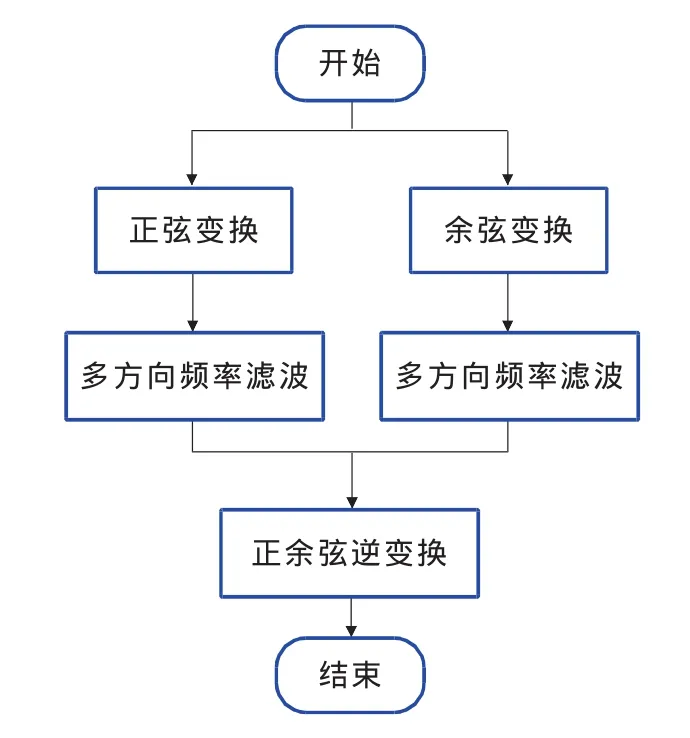
图3 多方向频域滤波流程图
图3为多方向频域滤波流程图,主要包括正弦变换与余弦变换、多方向频域滤波、正余弦逆变换3个过程。因为通过相移算法得到的包裹相位图存在2π相位跳变,若将包裹相位图直接通过频域低通滤波处理,将会丢失相位跳变信息。为保留相位跳变信息,先将原始包裹相位图进行正弦变换、余弦变换,变换后的正弦变换图、余弦变换图在相位跳变处变得连续,故能保留原来相位跳变的信息。设(i,j)为图像中任意一点,Io(i,j)为原始图像灰度值,Isin(i,j)、Icos(i,j)分别为正弦变换、余弦变换后的灰度值,则正弦变换、余弦变换公式为
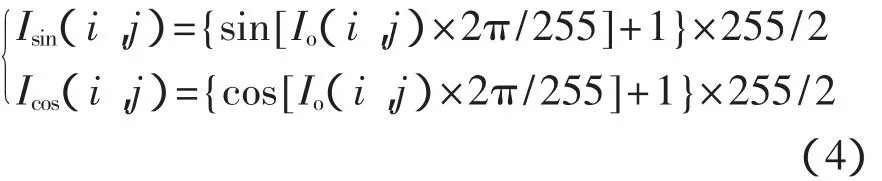
将变换后的正弦变换图、余弦变换图分别沿着不同方向进行一维低通滤波,每一个滤波方向的截止频率根据该方向上条纹疏密情况设定。由于错位方向条纹密度比其法向条纹密度要高,故在进行频域低通滤波时,错位方向法向滤波截止频率比错位方向滤波截止频率低,这样以便达到更好的滤波效果。将滤波后正弦变换图、余弦变换图进行逆运算,便可得到滤波后的图像。设Isin′(i,j)、Icos′(i,j)分别为滤波后的正弦变换灰度值和余弦变换灰度值,Ie′(i,j)为滤波后的图像灰度值,则逆运算公式为
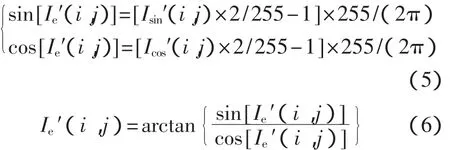
图4为多方向频域滤波各个过程图像。其中,图4(a)是原始剪切散斑干涉相位图[9],图 4(b)、图 4(c)分别是图 4(a)的正弦变换图、余弦变换图,图 4(d)、图 4(e)分别为图 4(b)、图 4(c)沿着水平、垂直、45°、135°4个方向进行一维频域低通滤波所得到的图像,每个方向的截止频率分别为:50,50,60,25。图 4(f)是图 4(d)、图 4(e)经逆运算后得到的包裹相位图滤波图。

图4 多方向频域滤波过程
3 滤波试验结果与分析
为验证上述方法有效性,本文用上述方法对两张包裹相位图进行滤波处理,并与中值滤波、正余弦滤波方法进行对比。
图5为包裹相位图滤波对比图,其中图5(a)是XY方向剪切散斑干涉包裹相位图,图5(b)是其7pixel×7pixel窗口3次中值滤波图,图5(c)是其正余弦滤波图(截止频率为50),图5(d)是本文提出的多方向频域滤波图(水平方向、垂直方向、45°方向、135°方向4个方向的截止频率分别为50,50,60,25)。
图6为轮胎缺陷包裹相位图滤波对比图,其中图6(a)是通过激光散斑轮胎无损检测仪检测轮胎内部缺陷获得包裹相位图,图6(b)是其5pixel×5pixel窗口2次中值滤波图,图6(c)是其正余弦滤波图(截止频率100),图6(d)是本文方法滤波图(水平方向、垂直方向、45°方向、135°方向4个方向的截止频率分别为 90,90,60,120)。

图5 包裹相位图滤波对比
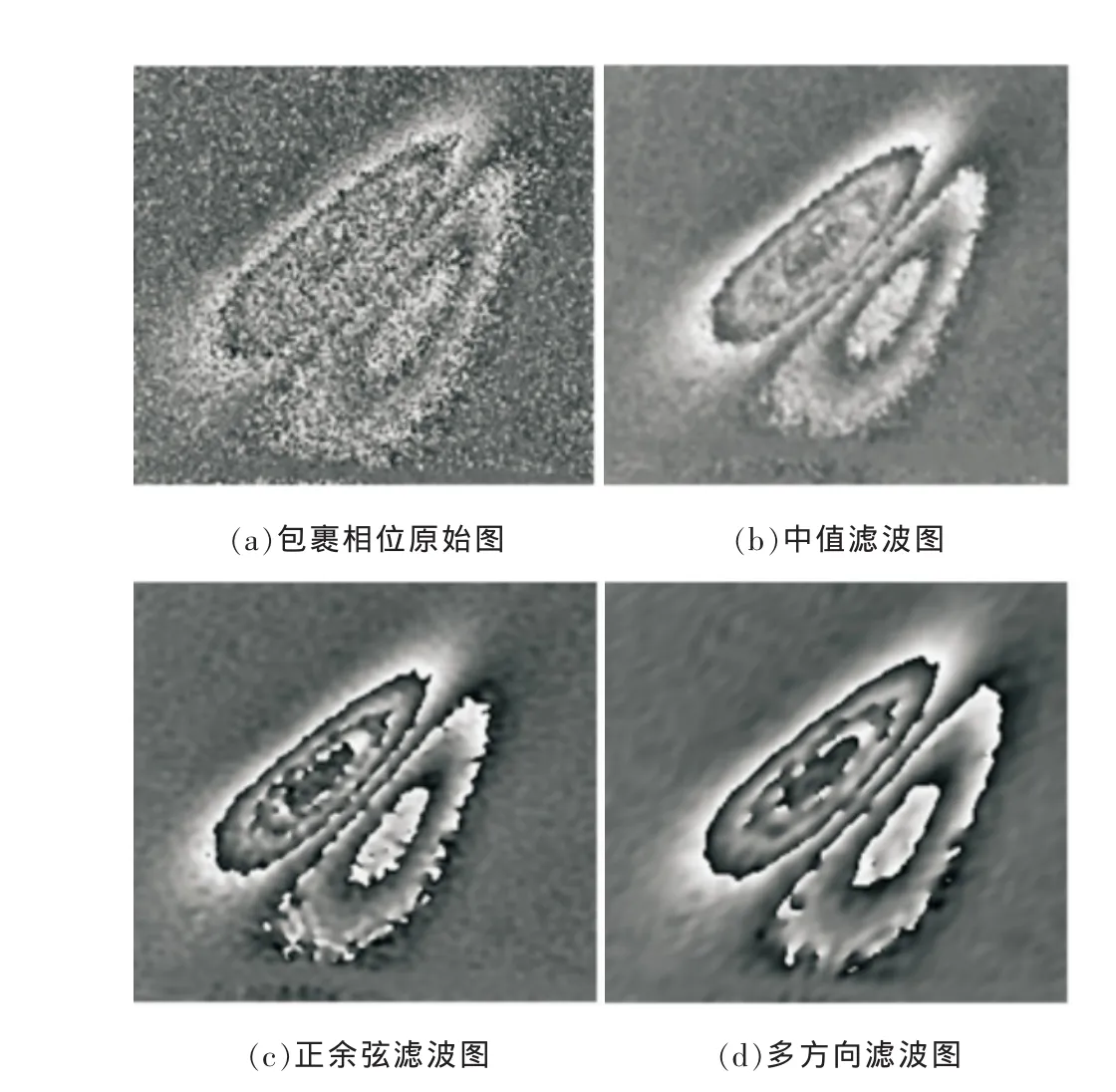
图6 轮胎缺陷包裹相位图滤波对比
由图可知,本文滤波方法在图像细节保持、噪声抑制方面都取得了良好效果。为了客观评价图片滤波质量,选取残差点数[10]、峰值信噪比RPSN[11]和图像细节保持指数EPI[12]3个评价参数来定量分析图片滤波质量。其中,残差点数是衡量噪声抑制程度的指标,残差点数越少、噪声抑制能力越强;峰值信噪比RPSN、图像细节保持指数EPI均是衡量图像细节保持能力的指标;RPSN值越大、细节保持越好;EPI越接近1,细节保持越好。
表1、表2分别为图5与图6滤波参数比较表,可以看出:1)3种滤波图像峰值信噪比都相差不大;中值滤波残差点数最少,其原因是图像条纹比较密,中值滤波丢失大量图像信息,也因此其边缘保持指数要比其他两种滤波方法小很多,表1中的中值滤波边缘保持指数分别是正余弦滤波、多方向滤波的27.199%、22.491%;表2中的中值滤波边缘保持指数分别是正余弦滤波、多方向滤波的43.753%、34.525%;2)多方向滤波残差点数分别是正余弦滤波的16.456%、36.555%,多方向滤波噪声抑制能力比正余弦滤波要强;3)表1多方向滤波的边缘保持指数分别是正余弦滤波、中值滤波的1.117倍、4.257倍;表2多方向滤波的边缘保持指数分别是正余弦滤波、中值滤波的1.255倍、2.869倍,多方向滤波的细节保持能力在这3种滤波方法中表现最好。综合考虑对激光散斑干涉相位条纹图的噪声抑制能力、细节保持能力,多方向滤波方法在轮胎激光散斑干涉相位条纹图的滤波处理应用中取得较好效果。
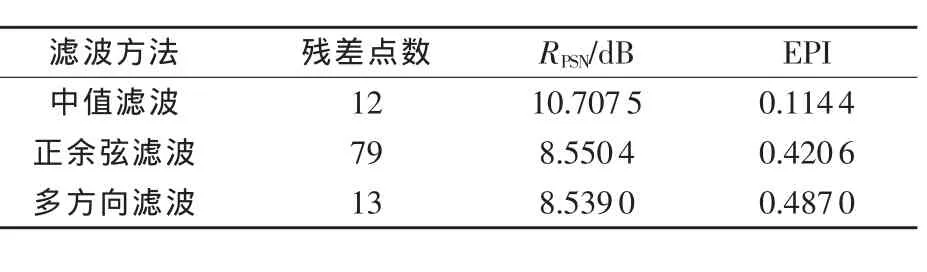
表1 图5滤波参数比较表
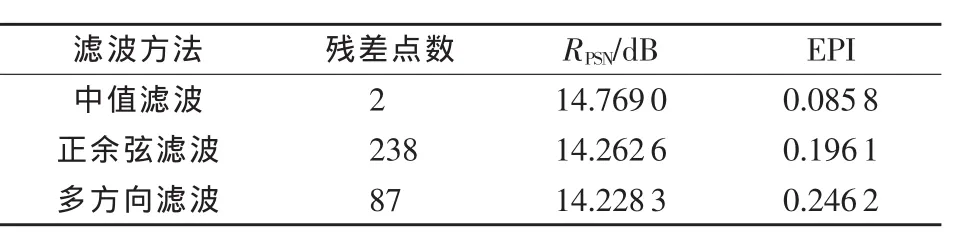
表2 图6滤波参数比较表
4 结束语
本文从激光散斑干涉相位条纹图的形成原理、特征、去噪方法等方面对轮胎激光散斑干涉相位图去噪问题进行研究,并根据轮胎缺陷散斑干涉包裹相位图条纹密度分布特点,提出了一种多方向频域低通滤波方法,定性、定量地对比分析该方法与其他方法的去噪效果。多方向频域滤波方法只需进行一次滤波就能有效滤除噪声,还能更好地保留图像边缘信息,在轮胎激光散斑干涉相位条纹图的滤波处理中具有很大优势。但该方法在每个方向滤波的截止频率需多次测试才能得到最好截止频率,下一步研究工作是根据每个滤波方向上的条纹密度来自适应调节每个滤波方向上截止频率,实现一种多方向自适应频域滤波方法。
[1] 王暐,王春平,付强.基于梯度的自适应椒盐噪声滤波算法[J].中国测试,2013,39(6):28-31.
[2] Pilevar A H,Saien S,Mina K,et al.A new filter to remove salt and pepper noise in color images[J].Signal Image and Video Processing,2015,9(4):779-786.
[3] Gao J Y,Wang K F.Study and design of exponential and Butterworth low-pass filters used for digital speckle interference fringe filtering[J].Optik,2013,124(2013):6713-6717.
[4]Qian K M.Two-dimensional windowed Fourier transform for fringe pattern analysis:Principles,applications and implementation[J].Optics and Lasers in Engineering,2007(45):304-317.
[5] LI C C,Chen T.Localized fourier transform filter for noise removal in electronic speckle pattern interferometry wrapped phase patterns[J].Applied Optics,2011,50(24):4903-4911.
[6] 王永红,李骏睿.散斑干涉相位条纹图的频域滤波处理[J].中国光学,2014,7(3):389-295.
[7] 蔡长青.散斑干涉计量关键问题研究及其应用[D].广东:华南理工大学,2013.
[8] Yao S N,Collins T.Hybrid method for designing digital butterworth filters[J].Computers&Electrical Engineering,2014,38(4):811-818.
[9]李骏睿.基于空间载波相移的激光散斑测量系统[D].安徽:合肥工业大学,2014.
[10]吴文娟.矿区SAR干涉图滤波方法研究-以南屯煤矿为例[D].江苏:中国矿业大学,2014.
[11]冯长江,毛博,薛冰.基于运动估计结合小波分析和运动补偿的视频去噪方法[J].中国测试,2013,39(5):1-5.
[12]龚胡,石强.基于平均梯度的边缘保持指数的图像质量评价[C]∥Proceedings of the 2011 International Conference on Information,Services and Management Engineering(ISME 22011)(Volume3),2011.
