激光干涉波形解调测量振动相位新方法

朱 沙，何天祥， 方 超， 林俊杰， 章 兵

（1.中国测试技术研究院，四川 成都 610021；2.中国航空工业集团公司北京长城计量测试技术研究所，北京 100095）

0 引 言

在工程测量领域，主要采用振动传感器套组对振动幅值和相位进行测量。当前，正弦逼近法是振动计量领域的一种振动绝对测量方法，由德国人首先提出并实现，其使用正交迈克尔逊激光干涉仪可同时测量振动的幅值和相应相位[1]，但是其测量系统结构复杂，建立费用高。

零差迈克尔逊干涉仪是我国振动计量领域里普遍使用的一类激光干涉仪。当前，利用零差迈克尔逊干涉仪建立的条纹计数法作为振动的绝对测量方法，只能测量振动幅值，无法测量振动相位[2]。本文介绍的振动幅值相位绝对测量方法，是在零差迈克尔逊激光干涉仪的基础上，利用高速数据采集卡和虚拟仪器技术实现的。振动台每发生1/2激光波长的位移，就会产生一根干涉条纹，干涉条纹经过光电倍增管输出类似于频率调制的正弦信号，数据采集系统以信号源信号为闸门信号对此信号进行采集，然后在LabVIEW平台上解调出振动位移波形，实现标准振动台的幅值和相位以及振动传感器数据的同时测量。该方法实现了振动幅值和相位等参数的自动化测量，为振动传感器的相位校准提供了新的途径。

1 振动参量的幅相特性

在正弦直线振动计量中，主要考核振动的3个基本参量：位移、速度和加速度，其中加速度是主要参量。在工程应用领域，一般采用振动加速度计来获得振动的加速度值，对于振动加速度计的检定和校准，是采用比较法和绝对法获得振动加速度计套组的复灵敏度。

加速度计的复灵敏度用频率的复值函数表示：

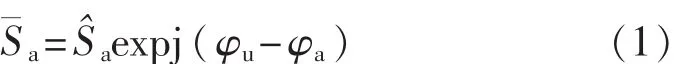
φu——加速度计输出信号的初相位；

φa——振动台加速度的初相位。

式（1）中的相移是加速度计电输出相位与机械振动输入相位的差值，即Δφ=φu-φa。加速度计灵敏度幅值a与相移Δφ在频域的变化曲线分别称为灵敏度的幅频特性和相频特性[3]。

2 零差迈克尔逊激光干涉仪

本方法采用零差迈克尔逊激光干涉仪。测量原理如图1所示，激光器发出的光束经分光镜分为两束：反射光束（参考光束）投向参考反射镜后反射回到分光镜，透过分光镜射向光电检测器；透射光束（测量光束）由固定在加速度上的反射镜反射后，回到分光镜反射，也投向光电检测器[2]。设参考光束的光强为E1，测量光束的光强为E2。

式中：E10、E20——参考光束和测量光束的光强幅值；

L1、L2——参考光束和测量光束的光程；

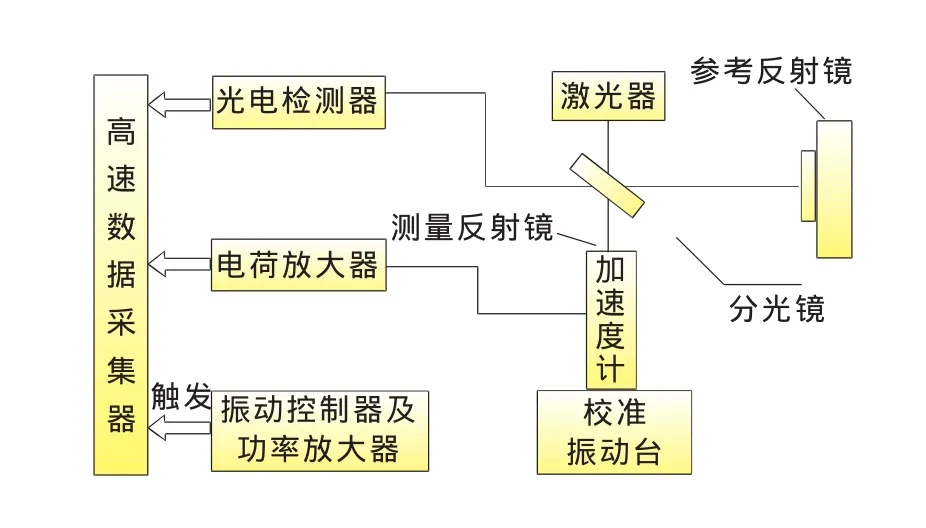
图1 测量原理示意图

ω0——光学角频率；

λ——光波波长；

φ——光波初位相。

光电检测器响应光信号的平均强度，光电流I为

用式（2）代入式（3）并舍去光电检测器不能响应的直流部分，在采样电阻取出的光电信号的交流电压U为

式中：d0cos（ωt+φo）——振动位移；

d0——振动位移单峰值；

ω——角频率；

φo——初位相；

L0——不振动时的光程差，简化后为恒定相位，在有运动干扰时，可表示为φ0（t）。

可把式（4）写成：

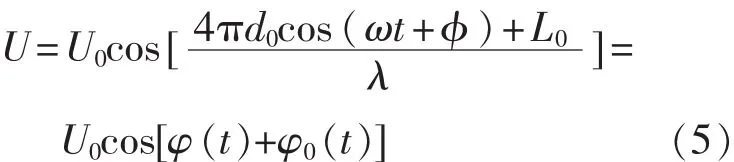
由此式可以看出在正弦振动的干涉波形（即采样电阻取出的光电信号的交流电压U）为类似于频率调制波形的信号[4]，如图2所示。

3 激光干涉波形解调方法

正弦振动的干涉波形类似于频率调制波形，使用高速数采采集光电信号一系列从正方向（或负方向）过零点的时间ti（i=1，2，3，4，…），注意t1、t2、…是非等时间间隔的（如图2所示）。

这个序列相邻两点之间的位移增量为±λ/2。若使用零差迈克尔逊干涉仪，计算N个整振动周期内从正（或负）方向过零点的数目Z，这个数目等于条纹计数法中的数目，由此可获得振动位移d0=λZ/（8N），其技术指标与条纹计数法相同。

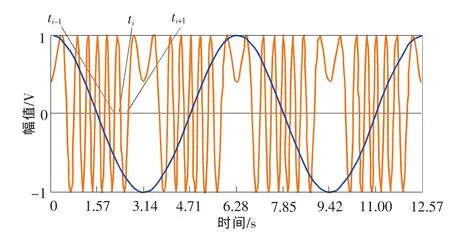
图2 光电信号（橙色）和振动位移信号（蓝色）的对应关系

振动位移信号x（t）为

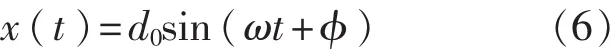
两个采样点的位移差Δx为

其中 Δf（ti）=1/（ti+1-ti）。

由此可得：

x′（ti）是一新的振动位移信号，其幅值和角频率与原振动位移信号x（t）相同，只是有90°的相位移动。

由于零差迈克尔逊干涉仪不能识别振动方向，但如果配合驱动振动台的正弦信号，参考信号源过零点的方向，则可以完全确定振动台的运动方向，由激光干涉波形复现振动台运动一致的波形。图2显示了激光干涉波形（橙色）和振动位移信号（蓝色）的对应关系。

设计采集方案如图1所示。由此得到的振动位移运动曲线与振动台运动一致，同步采集被校传感器的输出，则传感器输出信号对得到的振动信号作传递函数，可以得到传感器在此频率点下相应的幅相特性，其中的角度即为传感器的相移，从而构成振动测量系统的相位校准系统。为了获得更好的效果，可将变换后的x′用一个三角函数去逼近。即令：

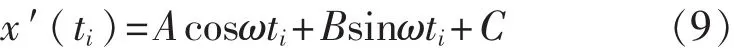
同样用最小二乘法获得A、B、C，并计算振动位移和相位。

4 设计方案实现与实验结果

振动台发生1/2激光波长的位移，就会产生一根干涉条纹，干涉条纹经过光电倍增管输出类似于频率调制的正弦信号，脉冲信号和标准信号源信号同时输入数据采集系统，数据采集系统以信号源信号为闸门信号对脉冲信号进行计数[5-6]。因此，脉冲信号就转换为脉冲数的序列，脉冲数的大小对应于周期时间内的位移值。本系统的LabVIEW软件平台是基于峰值点时间间隔求解的信号频率，通过查找脉冲序列最大值的方法，以及在最大值点前后3个点的比例运算修正得到最大值点和它的位置，从而确定波形峰值/波谷位置，再利用峰值处脉冲序列数的大小求解信号幅值。利用脉冲序列拟合和解调复现位移波形以及加速度幅值和相位[3，7-9]。幅值和相位测量系统前界面如图3所示。

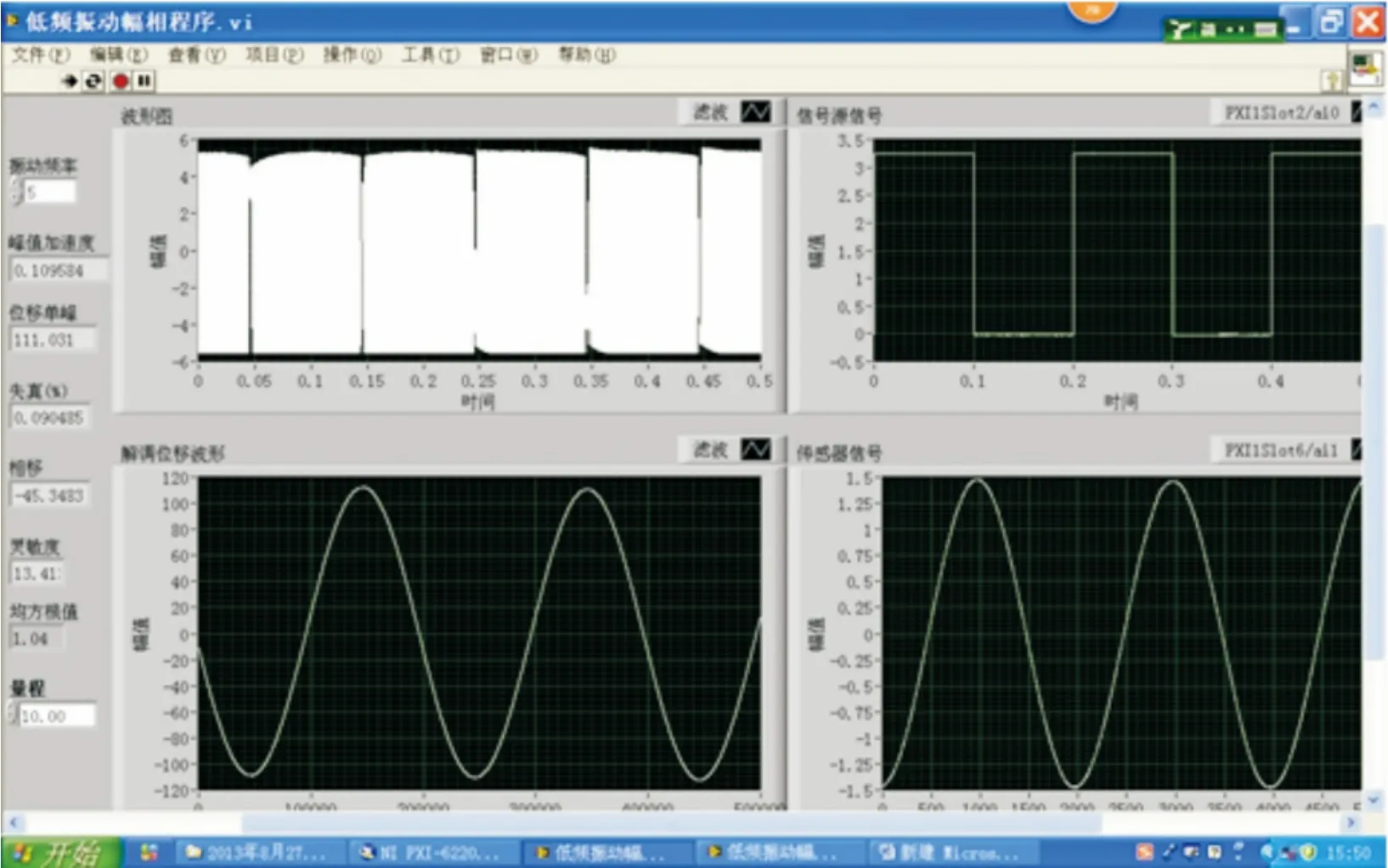
图3 幅值和相位测量系统前界面

表1 正弦逼近法与基于激光干涉波形解调测量振动相位的方法比较

本方法可实现激光干涉信号拟合波形、信号源输入波形、解调的位移波形、传感器输入波形、峰值加速度值、位移单峰值、失真度和相移值等波形和参数的计算和显示。本方法与正弦逼近法相位测量比对实验数据如表1所示，所用传感器为石英挠性加速度传感器。由表可知，本方法测量振动套组的相位与正弦逼近法测量数据基本一致，证明本方法是准确可靠的。

5 结束语

基于零差迈克尔逊激光干涉仪测量振动相位的方法，是正弦逼近法之外的新的相位绝对测量方法。相比于正弦逼近法，系统结构更简单、建立费用低。整个测量过程实现了自动控制、自动测量和实时显示等功能，使测量过程更为简便，对于振动台的参数控制也更加准确。

[1] ISO16063-11.Methods for the calibration of vibration andshock transducers-Part l：Primary vibration calibration by laser interferometry （third edition）[S].1999.

[2] Wabinski A W，Martens H J V.Time interval analysis of interferometer signals for measuring amplitudeand phase of vibrations.Proceedings of SPIE Second International Conference on Vibration Measurements by Laser Techniques.Berlin：SPIE，1996.

[3] JJG 233—2006压电加速度计[S].北京：中国标准出版社，2006.

[4] 赵洋，李达成.外差激光干涉仪的实现方法及其特点[J].计量技术，1996（7）：2-5.

[5] JJF 1265—1990低频垂直向振动基准操作技术规范[S].北京：中国计量出版社，1990.

[6] JJF 1263—1990低频水平向振动基准操作技术规范[S].北京：中国计量出版社，1990.

[7] 马明建.数据采集与处理技术[J].2版.西安：西安交通大学出版社，2005：39-42.

[8] 杨乐平.LabVIEW程序设计与应用[M].北京：电子工业出版社，2001：12-22.

[9] 陈锡辉，张银鸿.LabVIEW8.20程序设计从入门到精通[M].北京：清华大学出版社，2007：23-25.