DLS纳米粒度仪噪声剔除方法探讨与计量检定

吴国光，韩 鹏，鲁力维

（1.广东省计量科学研究院 广东省现代几何与力学计量重点实验室，广东 广州 510405；2.华南师范大学物理与电信工程学院，广东 广州 510006）

0 引 言

动态光散射技术是研究亚微米、纳米颗粒粒径及其分布的重要手段[1-2]。但由于光强散射信号较微弱，极易受噪声影响，小粒径颗粒更难准确测量。因此，国家质检总局发布检定规程JJG1104——2015，对DLS粒度仪的准确度与重复性等性能指标作出规定[3]。为使仪器能够满足要求，提高测量准确度，必须有效抑制噪声仪器。在噪声抑制方面，学者做过大量研究，主要从噪声来源、光子信号处理、反演算法等角度出发[4]。如张华东等[5]将噪声分为外部环境噪声与设备内部噪声，并提出针对性的抑制方法；王雅静等[6]针对短数据量信号信噪比较差的情况，采用小波包变换对信号进行去噪再进行相关运算；韩鹏等[7-8]基于光子计数率跳变的方法，剔除大颗粒引入的噪声，同时还研究了温度引起的噪声对测量的影响，提出双温度法剔除温度相关噪声；文献[9-10]则针对双颗粒混合的样品，采用多角度接收技术及基线误差补偿技术抑制双颗粒样品自相关函数的噪声；喻雷寿等[11]从反演算法角度出发，提出迭代CONTIN算法抑制噪声干扰，并模拟了不同噪声水平的抑制效果。以上研究都侧重于从实验现象角度对噪声进行分析，并提出针对性的解决方法，本文从另一个角度，将接收信号分类并从自相关曲线物理意义出发，提出剔除噪声的措施。

1 DLS纳米粒度仪测量原理与噪声来源分析

DLS纳米粒度仪是利用不同粒径颗粒的布朗运动引起散射光强涨落差异，由自相关函数反演求得颗粒的粒径及分布。图1为DLS纳米粒度仪结构示意图，激光通常采用632 nm红光，光子探测器用于接收特定角度下的散射光信号，通常为90°。相关器是粒度仪的关键模块，通过自相关运算得到散射光的相关函数，在计算机中利用反演算法求得颗粒的粒径分布。

从图1可以看出，DLS纳米粒度仪是一个典型的光学仪器系统，较易受到各种噪声的影响，包括背景杂散光、入射激光功率波动、光路中的尘埃与样品杂质散射、光电探测器等引起的噪声。为进一步抑制噪声，必须对来源进行分类，表1为噪声的来源与分类以及对系统的影响程度分析。

从表中可以看出，随机噪声对不同粒径的颗粒都有影响，其中，温度变化对粒度仪的测量准确性影响较大，因此需采用较好的温度控制器对样品池进行温控，而在线性相关噪声中，光电探测器的后脉冲效应对小粒径颗粒的测量准确度影响较大。后脉冲指由探测器的反馈机制输出的多个具有相关性的脉冲，影响的相关曲线是＜100ns的时间段，因此，本文提出基于噪声相关函数特征的剔除方法，目的在于同时降低随机噪声与线性相关噪声的影响，提高测量准确性。

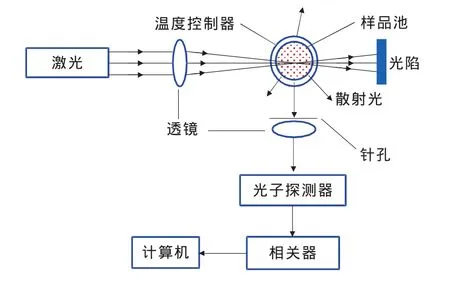
图1 DLS纳米粒度仪结构示意图

2 噪声对自相关曲线影响的理论分析与剔除

通过分析纳米粒度仪的噪声来源，本文提出基于噪声相关函数特征的降噪方法，即利用噪声的时间相关与无关性剔除噪声。

若入射光经过样品瓶中进行布朗运动的颗粒后，在特定接收角度下的散射信号强度为X，相关器采样时间为τ，相关运算时间T=Mτ。在理想状态下，即不考虑任何噪声情况下，接收到的光散射信号的自相关函数计算式为

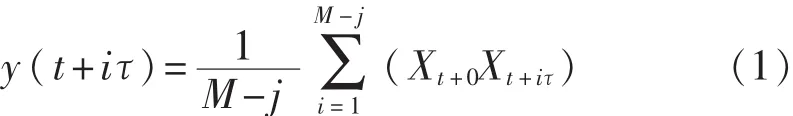
在实际条件下，系统必然存在噪声，若设接收到的随机噪声信号N、线性相关噪声信号A，则此时接收光散射信号y=X+A+N，根据自相关函数算法，放入样品时的光散射信号y自相关函数计算式为

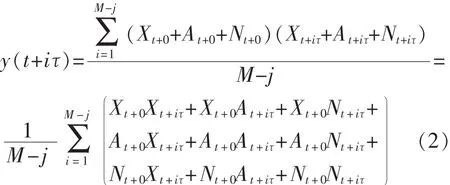
式（2）的物理意义是，原始的自相关函数是多个信号自相关与互相关运算的叠加，即颗粒布朗运动散射光信号、随机噪声、线性相关噪声自相关，还有三者之间的互相关运算结果的叠加。因此，线性噪声比随机噪声对测量结果的影响更大，在进行反演算法前，必须对信号相关函数进行去噪。

表1 噪声来源分类表

2.1 剔除自相关曲线受影响的数据点

从式（2）可以看出，若系统存在随机噪声或线性相关噪声，其在自相关函数延迟时间τ=0时，相关函数值最大。因此，必须剔除第1个自相关函数值。同时，当τ＞0，若随机噪声满足高斯分布，则自相关函数为0，即剔除第1个相关函数值后，其余不对相关曲线有影响；线性相关噪声由于存在相关性，其自相关函数不为0，应从相关曲线图形中判断是否有受到影响的数据点将其剔除。

2.2 缩短光程减少外部噪声

背景杂散光、光路尘埃与样品杂质散射等影响散射光信号强度，从式（2）可以看出，这些影响因素将与颗粒的散射信号相叠加，并且无法通过措施2.1剔除，将影响自相关函数与反演结果。因此，在仪器设计时应缩短散射光程，如接收光路采用光纤，一方面可将接收尽可能地接近样品池；另一方面，利用光纤的柔软性可更方便地与探测器连接，有利于仪器结构设计。

2.3 合理选择相关器运算采样时间

由颗粒粒径与衰减常数的关系式可以看出，大颗粒粒径衰减至基线时间较长，小颗粒粒径衰减时间则很短。因此，为更有效地获取相关曲线衰减段的信息，必须合理选择相关器采样时间。同时，从式（2）可以看出，线性相关噪声通过措施2.1、2.2也难以剔除，而目前研究已知的线性相关噪声中，光电探测器的后脉冲效应是一个重要的因素，其影响的主要是相关曲线500 ns以下的函数值，该时间段主要对小粒径颗粒或接收角度较小时有较大影响。原因在于，小粒径颗粒的散射信号衰减很快，为了获得更有效的衰减函数信息，必须提高采样时间，但提高采样时间又将引入线性相关噪声的影响。因此，应平衡获取有效信息与引入噪声之间的关系。

2.4 有效控制样品溶液浓度

样品溶液浓度影响测量结果，浓度过低，每秒光子数较少，信噪比低，自相关曲线难以反演得粒径信息，浓度过高，则可能导致光散射信号被多重散射，引起自相关曲线畸变。JJG 1104——2015描述了样品的制配方法，但很难判定溶液浓度多少合适，而本课题组经过多年的研究发现，采用每秒光子数判定溶液浓度较为简便，即每秒光子数（ACR）为3kc/s＜ACR＜50kc/s时，自相关曲线信噪比较大，反演结果较准确。

3 实验与结果分析

为进一步验证论文对于噪声的来源分析与对策，并对仪器性能进行计量检定，通过搭建实验平台进行分析。硬件主要包括：北京大学生产的HN1200型He-Ne激光器，其输出波长为632.8 nm的水平偏振光，Brookhaven公司的BI-9000AT相关器，BI-200SM广角仪、滨松公司BI-CCDS_A型光电倍增管，同时还包括制样所需的纯水器、超声分散器等。

样品制备：首先从Simplicity公司的紫外置水装置过滤出超纯水装入样品池，并用移液器（0～10μL）吸取一定量样品溶液并往样品池滴入1滴（本实验系统的样品瓶容积为24mL）。盖上瓶盖后摇匀，并放在BT-50超声波分散器中进行超声振荡，目的是将样品中团聚的粒子振散，使得溶液粒径保持相对一致；振荡后将瓶身用专用纸擦净并放入样品池。

实验采用的散射光接收角度为90°，温度为25℃，此时水的折射率为 1.331，粘度为 0.8899g/（m·s），单次实验测量时间为2min。

实验1：合理选择相关器采样时间

为验证采样时间对相关曲线的影响，针对同一样品，不同的采样时间进行对比实验，采样时间分别为0.1，0.5，1，5，10，20，50，100 μs，样品为美国 Duke 公司标称直径为90nm在聚苯乙烯微粒，最大延迟时间为100ms。图2为1μs与5μs时的相关曲线对比图。可以看出，延迟时间＜5μs时，自相关曲线存在较大畸变，因为提出采样速率时，也引入了线性相关噪声；而采样时间为5μs时，自相关曲线较平滑，此时并非不存在噪声而是由于采样时间较大，无法采集过快的线性噪声。

图3为不同采样时间的反演结果比较图，反演算法的基线采用扩展通道方法，以二阶累积法结果作为反演结果。

可以看出，由于采样时间＜1 μs时，自相关曲线存在畸变，其反演结果误差很大，其中采样时间为0.1μs时，误差最大，而采样时间＞5μs时，反演结果与标准值接近。因此，对于同一样品，选择合理采样时间对准确获得反演结果很有必要。

实验2：仪器示值误差与重复性实验

JJG 1104——2015主要考察DLS粒度分析仪的测量准确性及重复性指标，下面将对搭建的仪器进行性能检测。实验采用的样品为聚苯乙烯微粒，粒径标准值分别为美国Duke公司90nm、中国石油大学200，300nm颗粒。

图2 不同采样时间自相关曲线对比图

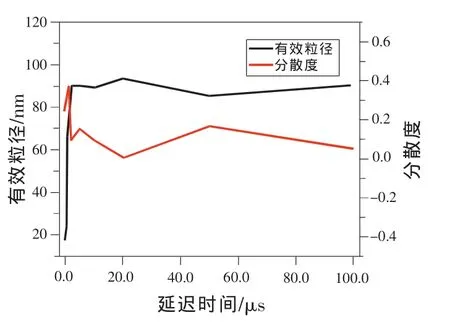
图3 不同采样时间的反演结果对比图

表2 实验测试数据表

1）仪器示值误差实验。依据规程分别对3个样品进行6次重复测量，并记录结果数据。测量结果取累积法的二阶反演值，数据见表2。可以看出，仪器示值误差最大为6.7%≤±12%，符合规程要求。

2）测量重复性实验。依据JJG 1104——2015规程，仪器的重复性采用＜100 nm粒径的颗粒进行8次重复测量，按照式（3）计算，本次实验采用粒径为90nm的颗粒。

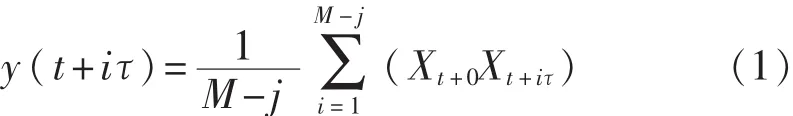
表3为实验测试结果，仪器重复性为0.9%≤3%，符合规程要求。

表3 重复性测量结果

4 结束语

论文研究了动态光散射纳米粒度仪的噪声来源，并对接收信号光散射信号进行分类，从自相关函数的物理意义出发，提出了剔除噪声的针对性措施，得到以下结论：1）剔除τ=0时的自相关函数值，若系统存在线性相关噪声，还应剔除其他受到影响的数据点；2）缩短光程、精简结构，减少外部噪声；3）合理选择相关器运算采样时间，平衡获取有用信息与可能引入噪声之间的关系；4）有效控制样品溶液浓度，提出以每秒光子数判断溶液浓度是否合适的简便方法。

[1] 陈哲敏，胡朋兵，孟庆强.动态光散射及电子显微镜纳米颗粒测量方法的比较研究[J].光散射学报，2015（1）：54-58.

[2] 刘桂强，杨冠玲，何振江，等.动态光散射在颗粒检测中的应用[C]∥第六届全国颗粒测试学术会议论文集，2005：19-22.

[3] JJG 1104—2015动态光散射粒度分析仪检定规程[S].北京：中国质检出版社，2015.

[4] Lou B Z.The Influence and Corresponding Solution of Noise in DLS Particle Sizing Experiment[J].Journal of Light Scattering，2008（20）：310-313.

[5] 张华东，娄本浊.DLS粒度测量实验中噪声的影响与克服[J].中国测试技术，2008，34（5）：126-129.

[6] 王雅静，申晋，郑刚，等.短数据量动态光散射颗粒测量信号去噪方法[J].强激光与粒子束，2010，22（6）：1388-1392.

[7] 向君，韩鹏.动态光散射中基于光子计数率的噪声剔除方法[J].中国粉体技术，2010，16（3）：22-25.

[8] 韩鹏，曹建新，向君.双温度法改进动态光散射仪测量准确度研究[J].中国粉体技术，2009，15（1）：1-3.

[9] 刘晓艳，申晋，朱新军，等.动态光散射技术的角度依赖性[J].光学学报，2012，32（6）：259-264.

[10]高珊珊，申晋，王雅静，等.多角度动态光散射技术中的基线误差补偿[J].光学学报，2013（33）：93-98.

[11]喻雷寿，杨冠玲，何振江，等.用于动态光散射颗粒测量的迭代 CONTIN 算法[J].光电工程，2006，33（8）：64-69.