以开放题为例，谈学生“发现问题”能力的培养

◆江苏省昆山市玉峰实验学校 仲崇恒

以开放题为例，谈学生“发现问题”能力的培养

◆江苏省昆山市玉峰实验学校 仲崇恒

发现问题、提出问题、分析问题和解决问题是问题解决的基本环节，其中发现问题是问题解决的源头，发现问题是学习真正发生的一个标志。开放题因其条件、结构、思路及答案等方面具备独特的优势，是培养学生问题意识的有力抓手。教师坚持从数学的角度科学规划，挖掘问题“源”， 培育问题“场”， 调节问题“阀”，引导学生有效观察、比较、猜想，实现问题的从无到有，从少到多，从分到合。

开放题；数学教学；问题解决；发现问题

问题解决能力是学生数学素养的基本成分之一。发现问题、提出问题、分析问题和解决问题是问题解决的基本环节，其中，发现问题是问题解决的源头，发现问题是学习真正发生的一个标志。布鲁纳说：“发现包含着用自己的头脑亲自获得知识的一切形式”。众多研究表明，不善于发现问题是我国学生的“软肋”，已经严重影响学生学习的有效性。长期以来，教师依靠机械重复的“题海战术”，让学生在枯燥乏味中巩固了所学知识，虽然能够又对又快地解答“常规问题”，然而，一旦面对“非常规问题”或实际生活问题，学生却是束手无策。新课程改革以来，数学课堂发生了许多有益的变化，数学命题从封闭走向开放，解题策略从单一走向丰富，问题答案从唯一走向多元。相对于传统的“封闭题”而言，非常规的开放题具有独特的优势。下面以小学高年级数学开放题为例，立足发现问题的层面来谈谈笔者的实验研究体会。

一、挖掘问题 “源”，引导问题发现，实现问题从无到有

艺术大师罗丹说：“对我们的眼睛来说，生活中缺少的不是美，而是发现。”其实，数学问题也是如此。数学源于生活，教师要指导学生从日常生活中发现问题，从数学的角度生发问题。笔者认为，教师的指导应该聚焦在有序性和启发性上。

图1

【例题】如图1，星球大厦第八层的写字楼共有16个面积相等的房间，阴影部分表示公用的过道。现将这层楼出租给四家公司做办公室用，要求：（1）每家公司 “三室一厅”，面积相等；（2）每家公司“三室一厅”的平面图形形状不同；（3）每家公司至少有一个房间与公共通道相通。你能设计出符合以上3个条件的方案吗？（《小学数学开放题举一反三》五年级分册第39页）

【实践】教师先呈现楼层平面图，说明 “阴影部分表示公用的过道”及 “四家公司租用”，提问：你看到了什么？

生：我看到有16个完全相同的正方形房间。我看到通道环绕着房间。

师：你们的观察都很有数学味道。如果让你来问大家一句话，你想说什么？

生：平均每家公司几个房间？每家公司租用的房间占这层楼的几分之几？

师：我觉得这两个问题太简单，不像五年级水平的问题。

生：在图中把分法画出来。有几种分法？

师：随便分吗？

生：不行，那太容易。要平均分。肯定有好多种分法。

学生手势纷纷比划，有竖着等分的，有横着等分的，有分成四个田字形的，有一家公司占据中间四格的……

师：大家的方案有个共同点，每家公司都是“三室一厅”，都有四个房间。随之比划出一家公司租用中间四格的方案，并用 “你想说点什么？”引导学生对提到的方案进行评判。

生：都划分成一样，没有个性。要不要增加一个要求？要求分的四个房间不一样。

师：这个提议非常棒。实际上房型也是多样的。

此时水到渠成，教师完整出示习题。学生尝试完成，然后展示交流。

教师组织回顾：刚才，大家想到的问题有这几类情况，图上有什么的问题，怎么平均分的问题，有几种分法的问题，还有方案是否合理的问题。原来我们可以发现这么多的问题。

“你看到了什么？”这是一个初级水平的铺垫问题，旨在让学生有一个心理准备。学生的观察点不尽相同，差异会带动学生由浅入深地思考。“你想到了什么？”教师启发学生对看到的和听到的刺激信息进行“预加工”。教师教给学生发现问题的方法，从提示发现问题的角度入手，问题的角度可以是归类或分类，也可以是知识的来龙去脉，使得学生通过一定的训练逐步掌握对数学知识或者现象的观察、追问、联想以及对比，使得真正待解决的问题慢慢成型，呼之欲出。

二、培育问题 “场”，激活问题增生，实现问题从少到多

现代认知心理学把知识分为陈述性知识和程序性知识。“是什么”“为什么”是陈述性知识；“怎么想”“怎么做”是程序性知识。换言之，知识的最初状态是一个询问或者质问，都是从问题开始。首先要“问”起来，其次，才有问题的诞生。最好的“问”是由学习者自己来问，由学习者互相来问。问，也许不需要答，带着问题学习，演习着一个有价值的问题从萌芽到成长的历程。

【实践】这道题目中已知条件涉及有四、五、六年级的人数，除了四年级人数已知外，其余两种数量未知。从数量关系句可以看到，条件之间具有依赖性，跳过五年级人数来求六年级人数是不可能的。此题的训练必须紧扣条件的分析和选择来补充问题。如果学生补上 “五年级有多少人？”“六年级有多少人？”“三个年级一共有多少人？”等问题后却不知道怎么解答，所提问题就不是真正意义上的对问题的发现。发现是数学现象、数量关系的具体认识或再创造，它需要大量知识层面为依托，必须有清晰的目标指向和行为设计。

教师出示三个条件，要求学生根据条件画出线段图（图2）。

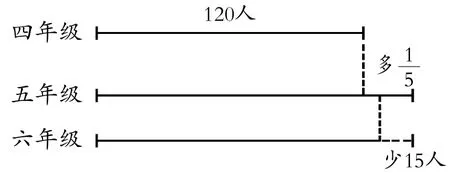
图2

教师巡视，提示用以表示六年级人数的线段要怎么画。

师：如果不知道四年级120人，你能否知道表示六年级人数的线段比四年级的长还是短吗？

学生讨论，达成一致认识，确定六年级的线段比四年级是长还是短，决定于四年级人数的对应的人数与15比较的结果。

师：想一想，根据什么条件，你能求出什么问题？

生：五年级多少人？五年级比四年级多几人？六年级多少人？

生：六年级和四年级相差多少人？六年级多五年级少几分之几？六年级人数比四年级多多少人？多几分之几？

生：四五六年级一共多少人？

师：请给这些问题整理一个顺序。

学生讨论交流，根据 “要求什么，必须先知道什么”的思维路径给问题排序。

师：你一开始想到了几个问题，后来又想到什么问题，又从同学交流中获得哪些问题？这些问题中最基本的问题，你认为是什么问题？

学生讨论，大家想到 “五年级有多少人”“六年级有多少人”这两个基本的问题。

师：还可以再往前找，就是五年级比四年级多的人数，也就是120人的是多少人。这个多的人数把握准了，随后提出加减问题就很容易了。

师：下面，请你把现在能想到的问题尽可能多地写出来，并列出相应算式，不计算。

课前抽样调查5人，所想到的问题数是1到3个，有三人写到“一共多少人”问题，但是有2人不能顺利解答。本课教学三天后，再次调查这5人，所补充的问题最少是4人，最多是11人。对于这道习题的处理，成功之处在于一个问题“场”的构建。这个“场”是数学活动场，也是思维的晒场，还是学生智慧的卖场。有一个学生后来对我说：“课前你的是你的，我的是我的；课后你的是我的，我的也是你的。”这就是合作交流的价值吧。

三、调节问题 “阀”，助推问题发展，实现问题从分到合

学生发现问题能力的形成必须要经过长期反复的训练才能够实现。在保证常态数学教材教学的前提下，找准教材内容与开放题之间的契合点，精心规划以发现问题为主旨的创新活动，教师在指导过程中应该不时调整激趣、启思、优化的思路，或精细，或粗放，或交流共享，或独立发现，抓住恰当时机组织学生深入研究数学现象及数量关系，以期发现更多有价值的数学问题，提高学生的数学思维水平，培育学生的发现能力和创新能力。

【例题】把一块长8厘米、宽4厘米的长方形铁皮做成一个高是厘米的无盖长方体铁皮盒。有哪几种不同的做法？容积最大是多少？（剪切、接头处损耗不计）（《小学数学开放题举一反三》六年级分册第15页）

【实践】前文两个案例主要立足 “问”和“答”来引导学生发现问题，借助的是集体力量。我们还认识到，更为经济和快捷的做法是动手做。动手做是一个信息提取过程，这是能动的“重建”过程，学生需要把记忆的内容重新改造。

学完长方体和正方体的表面积和体积的内容后，教师发给每人一张A4白纸，要求用好这张纸做一个无盖的纸盒。比一比谁做的纸盒容积大，前20名有奖。

学生面对操作性开放题，很自然想到的问题有：怎么做一个无盖的纸盒？需要把白纸裁成几个什么样的长方形？怎样保证材料不浪费？白纸不浪费时面积最大，那么容积就最大吗？纸盒应该有好多种做法，哪种情况容积才最大呢？怎样测量和计算？怎么做才能一次成功？等等。

学生七上八下的心理直接地表现在迟迟不动的手指上。稍待片刻，有学生在草稿本上画示意图，列了算式。画图、计算、比较，几番尝试下来，终于让学生有了动手剪切的底气。

这个动手做活动，把众多的问题集中为一个问题：怎样围容积最大？学生要回应这个问题，仅有动手是不够，还要时不时地拉开数学知识的阀门，想想长宽高，算算容积，在这一缓慢的过程中，学生经历了对情境的观察和分析，对“问题”信息的收集、选择和处理，感受认知冲突，形成问题意识。学生通过自主探索和学习，理解知识之间的内在联系，也体验到发现的兴奋感和完成任务的信心，从而激发内在动机，为以后的学习和思考积累了宝贵的活动经验。有了如此丰富实在的内隐的问题发现意识，问题的提出、分析及解决也必将风调雨顺，学生对问题解决就会有一个更加完整、和谐、从容的数学印象。

[1]杨传冈,徐正洲等.小学数学开放题举一反三[M].南京：南京大学出版社,2014.

[2]杨传冈.小学数学开放题数学的现状分析与对策探寻[J].现代中小学教育,2014（5）：32-34.

[3]陈永明名师工作室.数学习题教学研究[M].上海：上海教育出版社,2010.

[4]曹才翰,章建跃.数学教育心理学[M].北京：北京师范大学出版社,2006.

（组稿：杨传冈 编辑：胡 璐）

仲崇恒，江苏省昆山市玉峰实验学校，昆山市名教师，苏州市学科带头人。研究方向：小学数学教育。

本文系全国教育科学“十二五”规划教育部重点课题“数学开放题对小学生思维发展的具体影响评测”研究成果，项目编号：DHA140327。

G623.2

A

1671-0568（2015）34-0081-03