一种通信距离最小化的虚拟机分配算法

阮志强,陈志德

（1.闽江学院 福建 福州350108；2.福建师范大学 福建 福州350108）

一种通信距离最小化的虚拟机分配算法

阮志强1,陈志德2

（1.闽江学院 福建 福州350108；2.福建师范大学 福建 福州350108）

为了解决云资源分配过程中虚拟机通信距离较大，造成用户计算任务完成时间延长问题，提出一种最短通信距离的虚拟机分配算法。云资源管理器能够根据用户指定的虚拟机条件，将计算任务分割到合适的数据中心及其内部服务器，大大缩短了虚拟机之间的通信距离。仿真实验表明，与现有的贪婪算法和随机方法相比，提出的方法通信量更少，执行速度更快。

云计算；资源分配；虚拟机；延迟

资源分配是云计算自动化管理软件的核心功能之一，用户通常请求云为其分配虚拟机以完成计算任务。由于传统的数据中心由于距离较大，需要经过多个服务运营商，延迟会有很大的差异，而分布式数据中心[1]可以降低访问延迟。但是，云自动化软件的资源分配算法对用户程序的性能有直接的影响，因为有时需要将同一个计算任务的资源分配到多个相对较小的数据中心。即使一个数据中心能够满足用户请求，从容错性角度考虑，用户也不希望将所有的虚拟机设置在同一个数据中心内部。

数据中心内部可以看作分层结构，每个机架有一些固定的刀片服务器，每个刀片服务器由一些处理器组成(单核、双核或多核)。同一刀片上不同处理机上的虚拟机可以直接通信，而同一机架上的不同刀片服务器上的机器需借助机架顶部交换机实现通信，两个机架之间则使用聚合交换机。如果机架位置相隔较远，可能需要多层的聚合交换机。可见，某个应用程序的虚拟机之间的通信延迟取决于调度的物理机器的位置。

将单个虚拟机分配给某个数据中心及其内部的某个CPU属于图划分问题，该问题是将图分成大小相等的片，使得两个片之间的连通最少。另一个相关问题是最小k-切割问题，是将图分成k个集合，并最小化边的权值。如果集合的大小没有给出，而集合的个数必须是r，那么问题在多项式时间内可解[2]。如果r作为输入的一部分，问题是NP难或存在2-2r近似算法[3]。当给定集合的大小和固定值r，存在3-近似算法。

文中的目标是减少数据中心之间以及数据中心内部的通信量，同时最小化数据包传递的路径长度，以提高服务性能。整个资源分配过程可分为以下4步：

1)数据中心选择：确定放置用户虚拟机的数据中心。根据用户请求条件和系统可用性，用户虚拟机可能会被放置在多个数据中心。如何找到一个数据中心子集，满足资源需求的同时最小化数据中心之间的路径长度，是本文要解决的第一个问题。这是因为虚拟机之间通信延迟越大，任务完成时间越滞后，从而影响用户总体完成时间。

2)任务分割：一旦确定好满足用户请求的候选数据中心，需要为每个虚拟机指派一个数据中心。这一步的目标是最小化数据中心之间的通信量。

3)机架、刀片和处理器选择：为每一个选中的数据中心确定物理计算资源，同样的，优先选择机架间通信量的最低的物理机器。

4)虚拟机放置：将每个虚拟机放置在物理资源上（机架、刀片、处理器），并最小化虚拟机之间跨机架的通信量。

1 数据中心选择

数据中心选择问题可用看作子图选择问题，给定一个完全图G=(V,E,w,l)，顶点V表示数据中心，w表示数据中心内可用的虚拟机数量。E表示数据中心之间的路径，d表示路径的长度、跳数或最短路径的延迟。如果用户请求中包含最多放置虚拟机个数/每个数据中心这一限制条件，顶点的权重w就设为给定的最大值。反之，如果请求中包含最小放置虚拟机个数/每个数据中心，将权值低于最小值的顶点从图中移除。令m表示用户请求的虚拟机个数，问题变为找到一个子图G，它的权值之和至少是m而且子图的直径（即任意两个顶点间距离的最大值）最小。

算法1最小直径子图(Min Diameter Subgraph(G,m))

算法1描述找到最小直径子图的过程，首先对于每一个顶点v，找到一个以v为中心的星型拓扑，加入的节点以到v的长度递增排序，直到星型拓扑的权值大于m。子图的边由拓扑中节点的边得来。该算法同样计算生成子图的直径(DIA)，当一个节点加入时，当且仅当引入该节点导致边的长度大于当前的直径时，子图的直径才会更新。然后，对于找到的每一个子图，算法选择具有最小直径(L)的子图。

算法1的时间复杂度估计如下：第6行是将G中所有节点到v的距离按长度递增排序，得到d(v,ki)≤d(v,ki+1)，其中ki表示距离，共有n-1个节点，需要O(n log n)，n表示数据中心的个数。另外，每个节点执行一次repeat循环，加上计算直径需要n2（有n2条边）。因此，最差情况下算法1的时间复杂度是O(n2)。

2 内部机器选择

算法2最小高度子树(Min Height Tree(T,s,m))

机器选择的目标是找到可以降低机架间通信路径的机器，可以将数据中心内部结构看作一颗树，根节点代表核心交换机，子节点代表顶层交换机，孙子节点代表第二层聚合交换机，以此类推，最终叶子节点代表机架或者刀片服务器。在这颗树中，所有的叶子节点处于同一层，给每个叶子节点赋一个权值，表示该机架或刀片服务器当前可用的虚拟机数目。对于机器选择问题，主要是最小化任意两个虚拟机之间的通信距离，即找到一颗具有最小高度且叶子节点权值之和大于给定虚拟机请求大小的子树。与上一节类似，我们可以加入一些限制条件，比如，每个机架或刀片服务器内至多或至少应选择的虚拟机数量，只要改变叶子节点的权值就可以实现。

用m表示一个数据中心内需要放置的虚拟机数量，T是树，代表数据中心的计算和网络资源，对 T中的每个节点都设置两个变量：w(v)，表示从根节点到节点v的可用虚拟机数量，和h(v)，表示节点的高度。算法执行之前，只有叶子节点设置权值变量。算法2找到一颗根为s，叶子节点累积权值为m且高度最小的子树。算法执行后续遍历法，并为每个节点维护一颗具有m权值和的最小高度子树。算法2的时间复杂度是O(n)。

3 虚拟机放置

分配虚拟机给数据中心及其内部CPU问题属于图划分和k-切割问题，将用户请求表示成图G=(V,E)，顶点V表示任务或待放置的虚拟机，边E表示虚拟机之间的通信需求。这里的目标是将V划分成不相交的集合S1，S2，…Sk，使得不同分割集的顶点之间的通信代价最小。图的每一个分割集代表需要调度的虚拟机集合，这些虚拟机集合处于相同的数据中心（全局或云调度）或相同的机架（数据中心内部调度）。每个分割的大小受限于对应的数据中心或机架的可用虚拟机个数。与传统的图划分不同，这里可能不会指定每个分割集确切的节点数目，只要求每个划分的最大节点数，因为系统中可用的虚拟机往往比请求的要多。

算法3最大分割子图（Partition(G,M)）

算法3给出了一种图分割问题的启发式方法，输入是用户请求图G和每个分割集的最大节点数目M=m1,m2,…mk，集合M可以由算法1得到。算法3首先将可用容量m1,m2,…mk降序排列，然后利用for循环尽可能填充这些数据中心或机架。for循环每次选择一个虚拟机满足最大输入/输出带宽或邻居个数，并将其放置在数据中心或机架中。该虚拟机加入被调度的虚拟机集合Si，接着算法考虑Si中所有节点的邻居，找到拥有最大输入/输出通信量Comm(u)的节点u，并将节点u加入Si。整个算法一直重复，直到数据中心或机架中可用的虚拟机资源耗尽或者没有可调用的虚拟机。

可以利用Meng[4]提出的贪婪算法进一步提高查找分割集的效率，主要是研究不同分割子集中的任意一对节点，检查如果互换这一对节点是否可以降低带宽使用。或者考虑将一个节点从一个集合移到另一个集合，看是否能够提高可用的容量。该算法找到所有移动的可能性，并找出最好的策略。整个过程一直重复，直到达到给定的移动次数或者算法没有进一步提高为止。

算法3中每个节点 （虚拟机）执行一次 repeat循环，Comm变量可以用堆栈维护，对于每个节点，该变量为每个邻居至多更新一次，因此，算法3的时间复杂度是O(n2log n)。

4 实验分析

将提出的最短通信距离的虚拟机分配算法（Virtual Machine Allocation with Minimal Communication Distance,简称MCD）,与贪婪算法（Greedy[5]和随机选择/放置方法(Random)[6]进行比较。随机方法任意选择一个数据中心，并将请求的虚拟机尽可能多的放置在该数据中心内。如果一个数据中心无法容纳用户所有请求的虚拟机，可选择下一个数据中心，以此类推。贪婪算法每次都选择拥有最大可用虚拟机的数据中心，并将请求的虚拟机尽可能多的放置在该数据中心内。

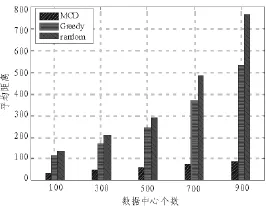
图1 不同数据中心的平均通信距离Fig.1 Average communication distance under different number of data centers

为了评估上述算法的性能，随机生成网络拓扑和用户请求，并衡量这些算法放置虚拟机后任意两个虚拟机之间的最大距离（直径）。实验设置如下：数据中心的位置从800×800的网格内随机选择，这些数据中心之间的距离是网格上点之间的欧几里得距离。每个分布式云包含的数据中心可以是100,300,500,700，到900，但是每个云包含的物理机器是相同的，也就是说一个数据中心的物理机器数量与其数据中心大小成反比。比如100个数据中心，每个数据中心包含50～100个物理机器。与500个数据中心，每个数据中心包含10～20个物理机器。这两个云的物理机器总数是一样的。

首先，将用户请求的虚拟机个数固定为1 000个，图1给出了虚拟机放置距离与数据中心个数之间的关系，可以看到，随着数据中心个数的增大，任意两个虚拟机的平均距离也增大。这是因为随着数据中心的增大，内部可用的物理机器数量减少，因此，同一个计算任务的资源被分散到多个数据中心中，使得通信距离变大。另外，MCD方法比贪婪算法和随机方法至少降低了80%的通信距离。

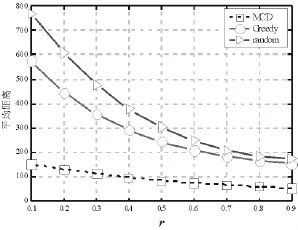
图2 指定用户限制条件的通信距离Fig.2 Communication distance given user requirement

接着，考虑用户指定额外限制条件下的通信距离。实验条件变为500个用户请求，每个用户需要10~20个虚拟机，由100个数据中心构成的云系统。限制条件是每个数据中心最多可放置的虚拟机个数，即分配的虚拟机个数占该数据中心总的虚拟机个数的比例，用r表示。图2给出了3个比较方案与限制条件r的关系。显然，随着r的增大，虚拟机之间的平均距离缩短，这是因为同一数据中心要求放置的虚拟机数量增大，大部分虚拟机之间的通信限制在数据中心内部。当r分别为0.1和0.9时，MCD的通信距离是贪婪算法的1/5和1/3，是随机方法的1/7和1/4。从图2可以还看出，通信距离可以通过参数r动态调整。

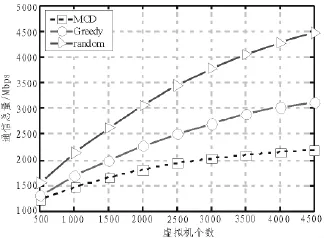
图3 系统通信总量比较Fig.3 Comparison of total system communication

图3给出了3个算法的通信总量与虚拟机请求数量的关系，实验中给定虚拟机之间的通信需求和每个数据中心的可用容量，其中，虚拟机的带宽需求从0~1 Mbps之间任意选择，数据中心个数设为500，每个实验重复20次，并取平均值。对每个虚拟机请求，随机算法任意指派一个数据中心，贪婪算法按照数据中心的可用容量降序排列，并尽可能将虚拟机放置在最大可用空间的数据中心内。当选择虚拟机时，总是选择拥有总通信量最大的虚拟机。从图3可以看出，随着请求虚拟机的增大，系统总通信量升高。在同样的虚拟机请求大小条件下，贪婪算法比随机算法大约降低22%的通信量，而MCD比贪婪算法大约降低18%

5 结束语

文中首先介绍了分布式云的作用和运行机制，重点阐述了基于虚拟化技术的资源管理方法。然后将虚拟机整合问题划分为4个步骤，即数据中心选择、任务分割方法、内部机器选择和虚拟机放置。为降低虚拟机之间的通信延迟，提出了一种最小直径子图的数据中心选择算法，基于最小高度子树的内部机器选择算法，以及最大分割子图的虚拟机放置算法。实验结果表明，本文提出的虚拟机整合算法MCD能够大大降低虚拟机之间的通信距离（延迟）。

虽然本文的虚拟机整合算法能够降低虚拟机的通信延迟，但由于系统的负载不断发生变化，虚拟机整合还需要综合考虑CPU的利用率、内存占用情况、以及网络带宽资源，下一步工作将研究虚拟机动态迁移的方法，使得系统的负载均衡化，从而降低系统总能耗。

[1]Alicherry M,Lakshman T.V.Network aware resource allocation in distributed clouds[C]//Proceedings of 31th IEEE International Conference on Computer Communications,INFOCOM 2012,2012:963-970.

[2]Eisenschmidt E,Haus U.A polynomial time approximation algorithm for the two-commodity splittable flow problem[J].Mathematical Methods of Operations Research.2013,77(3): 381-391.

[3]Ravia R and Sinhab A.Approximating k-cuts using network strength as a Lagrangean relaxation[J].European Journal of Operational Research,2008,186(1):77-90.

[4]Meng X,Pappas V,and Zhang L.Improving the scalability of data center networks with traffic-aware virtual machine placement[C]//Proceedings of 29th IEEE International Conference on Computer Communications,INFOCOM 2010, 2010:1-9.

[5]裴养,吴杰,王鑫.基于粒子群优化算法的虚拟机放置策略[J].计算机工程,2012,38(16):291-293.PEI Yang,WU Jie,WANG Xin.Virtual machine placement strategy based on particle swarm optimization algorithm[J].Computer Engineering,2012,38(16):291-293.

[6]TANG Zhuo,MO Yan-qing,LI Ken-li,et al.Dynamic forecast scheduling algorithm for virtual machine placement in cloud computing environment[J].The Journal of Supercomputing, 2014,70(3):1279-1296.

A virtual machine allocation algorithm with m inimal communication distance

RUAN Zhi-qiang1,CHEN Zhi-de2
（1.Minjiang University,Fuzhou 350108,China；2.Fujian Normal University,Fuzhou 350108，China)

Traditional resource allocation algorithm of cloud computing does not consider the communication distance of virtual machines,which may increase the complete time of user task.To address this problem,we propose an efficient virtual machine algorithm that includes data center selection algorithm and internal infrastructure assignment algorithm.Users can specify their requirements when requesting virtual machines,the resource allocator can partition this request into a few suitable data centers and their internal servers,so that the distance between any pairs of virtual machines is shortest.The results show that the proposed algorithms outperform greedy-based approach and random selection method in communication traffic and executing time.

Cloud computing；resource allocation；virtual machine；delay

TN91

A

1674－6236（2015）10-0001-04

2014-11-23 稿件编号：201411196

国家自然科学基金项目(61202462);福建省自然科学基金项目(2014J05079);福建省资助省属高校科研专项(JK2013043);福建省教育厅重点项目(JA13248);闽江学院科研启动项目(YKQ13003);教育部互联网创新平台开放基金项目(KJRP1301)

阮志强(1982—)，男，福建莆田人，博士，讲师。研究方向：云计算、分布式存储。