基于GA-DS的多神经网络故障诊断方法

张雷，黄奕宏,翁胜龙

（华南理工大学 机械与汽车工程学院，广东 广州 510640）

基于GA-DS的多神经网络故障诊断方法

张雷，黄奕宏,翁胜龙

（华南理工大学 机械与汽车工程学院，广东 广州 510640）

针对基于信息熵的神经网络证据形成过程需要专家经验确定参数这一不足，提出一种改进方法，即用遗传算法(Genetic Algorithm,GA)进行寻优，自动确定参数，其实质是利用了遗传算法的高效的并行寻优能力和对初始种群的较低的敏感性，通过训练样本自适应调整证据形成过程中的参数，提升DS(Dempster Shafer)证据理论的融合效率。对多类轴承故障数据的诊断结果表明，该方法(GA-DS)能够自动调整神经网络的证据形成过程，从而有效地降低了融合过程中证据的冲突性，并且显著提高了诊断精度和稳定性。

信息熵；神经网络；遗传算法；证据理论；故障诊断

神经网络以其优良的泛化性能被广泛应用于机械故障诊断[1]。对于神经网络，特征维度较低难以有效描述分类对象，维度较高则大大降低神经网络的训练速度和分类性能；证据理论常用于解决神经网络这一缺陷，通过融合多个低维特征空间的神经网络分类结果，起到不同分类结果之间的互补，并消除冗余，大大提高了分类精度和速度[2]。但是证据理论在合成高度冲突证据的性能稳定性较差，很大程度上取决于证据的形成过程。

针对神经网络的证据形成过程，本文提出一种基于遗传算法的改进方法，依据训练样本自适应调整证据形成过程，有效地消除不同神经网络形成的证据之间的冲突性。通过对轴承故障分类，结果表明该方法具有较高的正确性和稳定性。

1 DS理论和神经网络证据形成过程

设识别框架Θ={B1，B2，…，Bc}，c为命题个数;n个证据进行组合，证据集E={E1，E2，…，En}，各证据对应的基本概率赋值函数为mi(i=1,2…n),分配给Θ中命题Bj(j=1,2…c)的基本概率赋值(BPA)为mi(Bj)，则DS合成公式为:

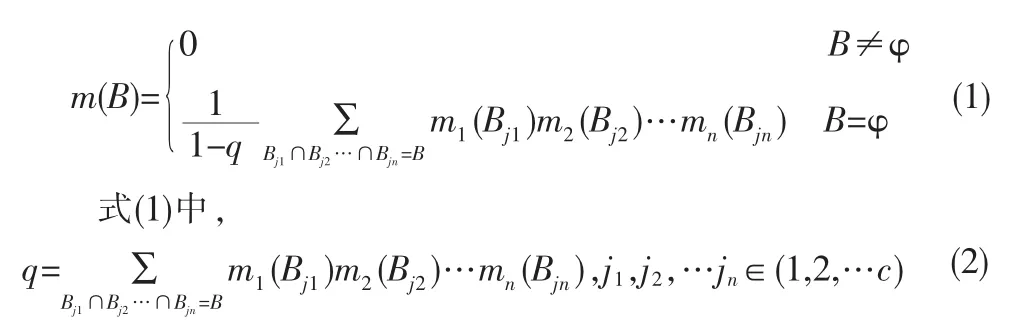
q为冲突系数，q∈[0,1]，当冲突系数较大时，DS理论融合结果常有悖常理。为了解决DS理论应用于多神经网络融合过程中冲突系数较大的问题，文献[3]提出了一种根据信息熵的神经网络证据形成过程。信息熵是由香农提出的，是用来描述信息的不确定性。信息熵值越大，信息的不确定性越大，提供的信息度就越小，所以该信息在融合过程中被保留的比例越小，所做修正越大，信息熵的计算公式为：

其中si为信息,这里si=pi,pi为神经网络输出归一化结果，当p1=p2…=pn=1/n时，信息熵到达最大Hmax=-log2(1/n)，此时不确定性最大。以Hmax为基础，计算各神经网络输出的信息熵H，通过式(4)得到对应的保留因子α：

λ是指数因子，表征保留因子α与信息熵H之间的非线性关系。各类的BPA为：

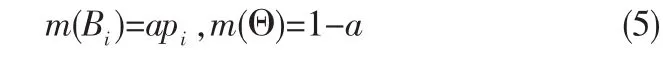
以一个三分类为例，对同一测试样本神经网络1、神经网络2、神经网络 3得到的(p1，p2，p3)分别为(0.1 0 0.9),(0.4,0.4, 0.2),(0.33 0.33 0.34),信息熵值大小：神经网络3＞神经网络2＞神经网络1，如图1，在相同λ值下，信息熵越大，保留因子α越小；当信息熵不变时，保留因子α与λ反相关，尤其当信息熵很大时，如神经网络3曲线，α随着λ的增大而急剧下降；随着信息熵的增大，α对于λ的取值敏感程度而增大。可见，λ的合理取值对证据的形成过程十分重要，尤其是当神经网络输出不确定性较大时。但对于λ的确定需要依据专家经验参考文献[3]，不利用于智能自动诊断，本文提出用遗传算法对其进行改进，提出基于GA-DS的多神经网络模型。

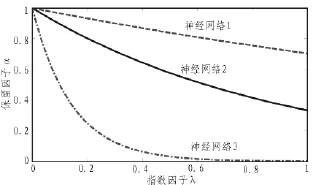
图1 保留因子α随指数因子λ的变化曲线Fig.1 The retention factor a variation curve depended by exponential factor λ

2 遗传算法

遗传算法[4]广泛应用于参数优化，适用于解决NP问题，是一种并行随机搜索最优方法，较好地避免陷入局部极值点。遗传算法的思想是“优胜劣汰，适者生存”，模仿生物进化中的杂交与变异，保证遗传算法的寻优过程快速、有效，并且初始种群对其寻优结果影响较小，有很好的鲁棒性[7]。

3 基于GA-DS的多神经网络模型

在用DS理论融合多神经网络之前，提出一种基于遗传算法的神经网络证据自适应形成过程，形成一种基于GA-DS的多神经网络模型，用于故障分类，基本步骤如下：

1)将样本分为训练样本，测试样本。按着一定比例，将训练样本分为训练样本a，训练样本b。

2)用训练样本a来训练各特征空间所对应的神经网络，确定各神经网络各层的权值和阈值。

3)用训练样本b输入训练好的各神经网络，通过含指数因子λ的证据形成过程，得到各神经网络的BPA，用DS理论融合各BPA，进行故障分类，最终得到训练样本b的诊断正确率，这一正确率作为遗传算法的目标值，通过遗传算法的优化过程来确定λ，如图2(a)。

4)将训练样本a与训练样本b的合集来重新训练各神经网络，重新确定各神经网络各层的权值和阈值。

5)将测试结果输入参数重新确定的神经网络以及λ确定的BPA形成过程，经DS融合得到最终的诊断结果，如图2(b)。

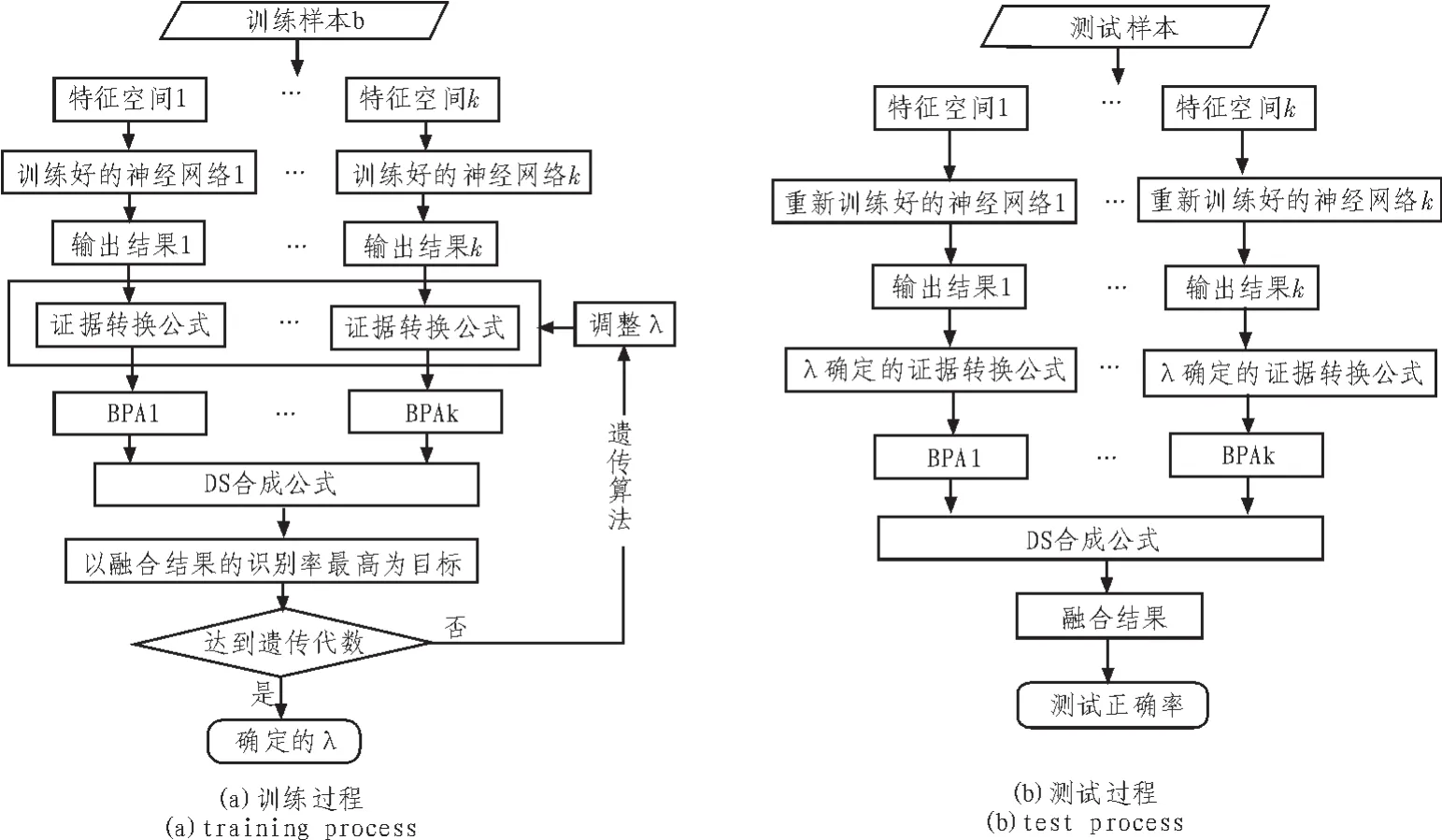
图2 GA-DS优化过程与测试过程Fig.2 Optimum and test process of GA-DS

4 实验验证

针对西储大学驱动端轴承滚动体四种不同故障程度的数据[5]进行分类，故障程度分正常、轻度点蚀、中度点蚀、重度点蚀四类,采样频率为12 000 Hz，在4种载荷下采集。对每种故障程度，各载荷下提取15个样本，每种故障程度共60个样本。

训练样本由载荷0HP、1HP、2HP各1/3的样本构成，共60个；测试样本由前3个载荷各剩余的2/3的样本与载荷3HP的全部样本构成，共160个。针对GA-DS方法，训练样本按照3:2的比例随机分为训练样本a和训练样本b。

根据滚动体故障的非线性、非平稳性，提取了样本的4类特征，构成4个特征空间如表1所示，时域特征分别为均方根值、峰峰值、峭度、偏斜度、方差、均值、波形指标、峰值指标、脉冲指标、方根幅值10个特征。EMD特征，是将时域信号进行EMD分解，取前3个本征模量[6]，各本征模量提取上述10个时域特征，共得到30个特征。将时域信号以db1为母小波，进行4层小波包分解得各分量的能量和熵分别得到小波包分量能量分布特征和小波包分量分布特征[7]。

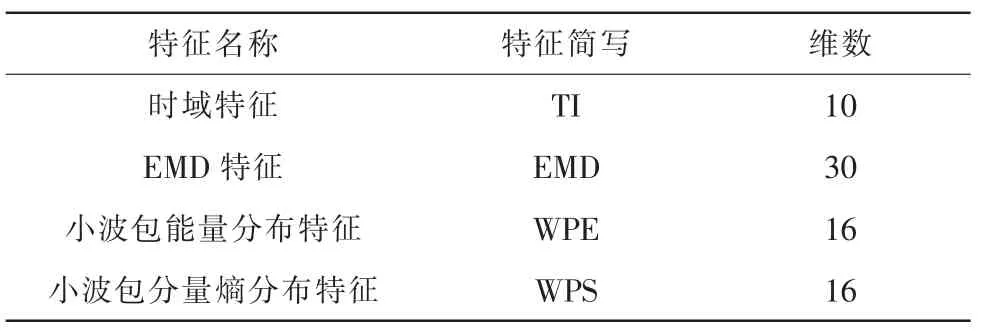
表1 特征提取方法列表Tab.1 The list of feature extraction method

分别单一特征空间神经网络进行分类以及采用DS和GA-DS方法融合4个特征空间神经网络进行分类，重复10次，结果如表2所示。

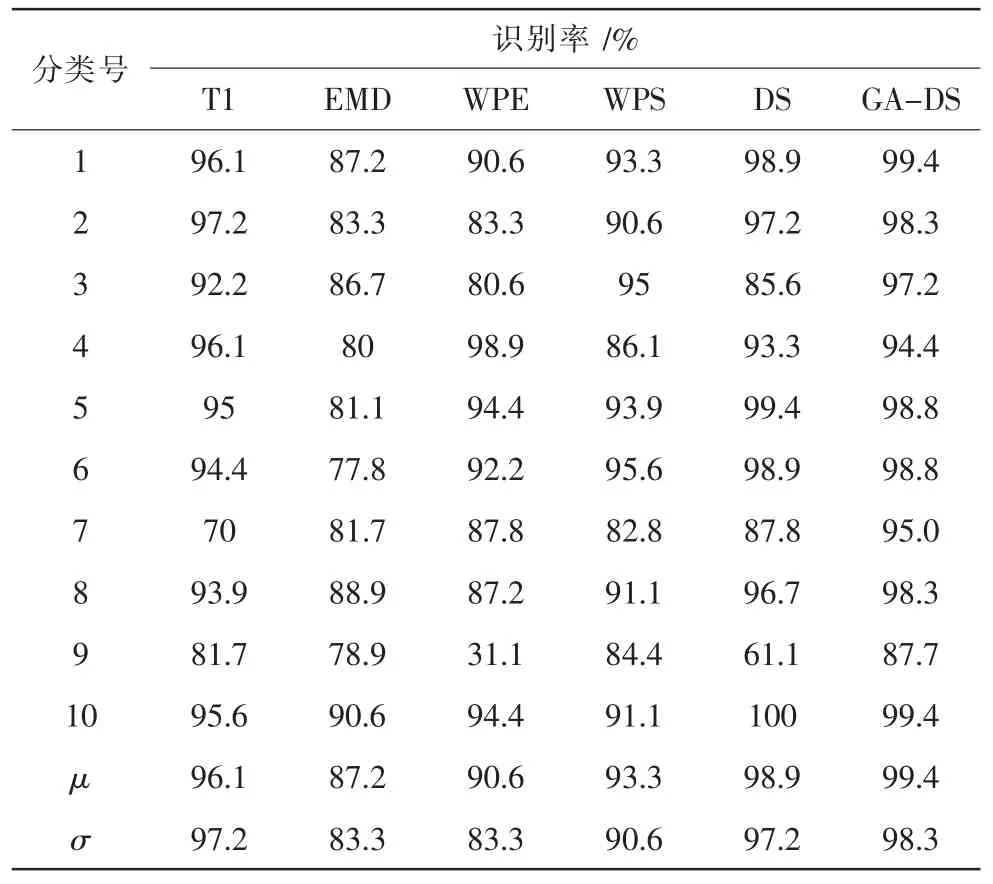
表2 测试样本的识别结果对比Tab.2 Identification results com parison of test sam ple

相比于DS方法，GA-DS方法得到的识别率的平均值为96.8%，标准差为3.4%，而DS方法得到的识别率的平均值为91.9%，标准差为11.9%，GA-DS方法明显优于DS方法。第3、7、9次融合过程中，DS得到识别率明显低于GA-DS方法，特别是第7次过程，DS得到的识别率为61.1%，而GA-DS得到的识别率为87.7%。DS这3次的融合识别率很低，是因为这3次融合过程中，4个特征空间的诊断结果的冲突性很高，导致DS融合识别率明显下降。可见GA-DS的自适应过程，能够较好地消除不同特征空间的证据冲突性，提高了融合诊断的准确性。

对同一训练样本b，遗传算法的初始种群的随机性，会导致优化结果λ的波动。所有用GA-DS对同一优化过程重复10次，得到结果如图3所示。

由图3(a)可知，GA-DS得到的平均识别率的最高值为96.8%，最低值为95.6%，平均值为96.2%；由图3(b)可知，识别率的标准差的最小值为3.4%，最大值为3.9%，平均值为3.66%。可见，GA-DS的最终识别率会有波动，但是波动较小，整体表现的都维持在较高的水平。

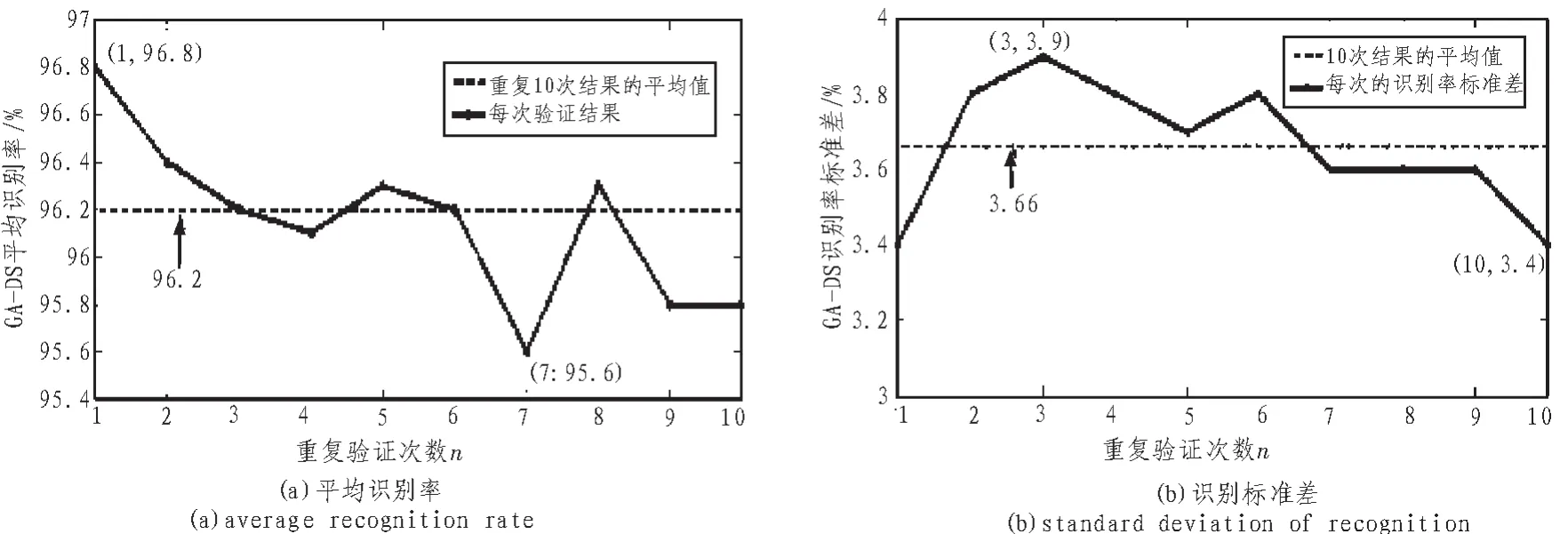
图3 GA-DS稳定性验证结果Fig.3 Results of the GA-DS’s robust stability test

5 结论

轴承故障的诊断问题一直是个难点，特别是轴承的滚动体故障，通过上面实证分析可知，利用单一的故障空间来对其进行不同故障程度进行分类，得到的识别率往往较低，且稳定性较差，而通过DS方法融合多个特征空间的分类结果而得到的识别率与这几个特征空间的分类结果的冲突性密切相关，当冲突性较大的情况下，DS方法得到的识别率很低。通过研究发现，GA-DS方法能够自适应的调整由各特征空间对应的神经网络的输出结果转换到证据的过程，尽可能地消除证据间的冲突性，融合结果具有稳定且较高的识别率。

参考文献：

[1]吴蒙,贡壁,何正亚.人工神经网络和机械故障诊断[J]，振动工程学报,1993,6(2):153-163.WU Meng,GONG Bi,HE Zheng-Ya.Artificial neural networks and machinery fault diagnosis[J].Journal of Vibration Engineering，1993,6(2):153-163.

[2]张池平,张英俊,苏小红,等.一种基于神经网络和证据理论的信息融合算法[J].计算机工程与应用，2006(1):174-176，179.ZHANG Chi-ping,ZHANG Ying-jun,SU Xiao-hong,et al.An algorithm of data fusion based on neural networks with DS evidential theory[J].Computer Engineering and Applications，2006(1):174-176，179.

[3]Valente F.Combination of acoustic classifiers based on dempster-shafer theory of evidence[J].IDIAP Research Institute,2006,3(2):23-30.

[4]余有明,李玉树,阎光伟.遗传算法的编码理论与应用[J].计算机工程与应用,2006(3):86-89.YU You-ming,LI Yu-shu,YAN Guang-wei.Encoding theory and application of genetic algorithm[J].Computer Engineering and Applications，2006(3):86-89.

[5]Loparo K A.Bearing data center[EB/OL].[S.l]:Case Western Reserve University[2008-06-20].http://www.eecs.cwru.edu/laboratory/bearing.

[6]王红军,付瑶.基于多项式拟合的EMD端点效应处理方法研究[J].机械设计与制造,2010(10):197-199.WANG Hong-jun,FU Yao.Study of polynomial fitting technique for EMD end effect[J].Machinery Design&Manufacture,2010(10):197-199.

[7]车红昆,吕福在,项占琴.多特征 SVM-DS融合决策的缺陷识[J].机械工程学报,2010,46(16):101-105.CHE Hong-kun,LU Fu-zai,XIANG Zhan-qin.Defects identification by SVM-DS fusion decision-making with multiple features[J].Journal of Mechanical Engineering,2010,46(16): 101-105.

M ultiple neural network fusion method for fault diagnosis based on GA-DS theory

ZHANG Lei,HUANG Yi-hong,WENG Sheng-long
（College of Mechanical&Automotive Engineering,South China University of Technology,Guangzhou 510640,China)

A improved method for neural network evidence formalism process based on information entropy was presented solve the shortage that the parameter definition relied on expert experience,where the parameter in evidence formalism process was defined automatically by GA method among training samples,with a high efficiency of parallel optimization and a low sensitivity of initial population,and the fusion efficiency of DS method was promoted.The improved method was verified in the multi-class bearing fault data processing,the evidence conflict in the fusion process was eliminated effectively,and the rate of fault diagnosis was improved remarkably in stability by adjusting the neural network evidence formalism process automatically.

information entropy;neural network;GA method;DS method;fault diagnosis

TN602

A

1674－6236（2015）10-0014-04

2014-09-14 稿件编号：201409113

张 雷(1990—)，男，江苏南通人，硕士。研究方向：车辆性能与故障诊断。