新型类Lorenz系统的控制研究

周群利

(芜湖职业技术学院电气工程学院,安徽芜湖241006)

新型类Lorenz系统的控制研究

周群利

(芜湖职业技术学院电气工程学院,安徽芜湖241006)

新型类Lorenz系统;输入-状态线性化;混沌控制

采用输入-状态线性化方法对新型类Lorenz系统进行控制.首先,对受控系统检验其能控性和对合性,当满足线性化条件时,运用微分几何中的Lie导数和Lie括号运算将非线性模型转化为线性模型,即将非线性系统的控制问题转化为线性系统的控制问题.然后,再对线性化后的系统设计线性状态反馈控制律,并适当选择反馈增益.由此,既能对极点任意地进行配置,使系统的三个状态变量均稳定地收敛于零,从而消除混沌.仿真结果证明了该方法的有效性.

20世纪90年代之后,控制混沌问题的研究已成为科学和工程界的前沿课题之一,各种控制混沌的方法层出不穷[1,2].在以OGY方法及其各种变形为代表的专门用于混沌系统的控制方法受到广泛关注的同时,人们也在研究把自动化领域已有的成果运用于混沌系统的控制.Hartley首先将经典控制方法用于控制混沌[3].之后,一些国内外学者通过局部线性化的传统线性反馈方法对混沌的控制问题进行了研究,进而非线性控制的一些理论开始应用于混沌的控制[4,5].在本文中,笔者以一种新型类Lorenz系统为基础,采用输入-状态线性化方法进一步研究其混沌现象的控制问题.

1 新型类Lorenz系统的数学模型

文献[6]提出了一种新型类Lorenz系统,其数学模型为：

(1)式中,x,y,z为系统的状态变量,g、d是系统参数,当g=0.1,d=0.4时,(1)式具有非常丰富的非线性动力学行为,系统处于混沌状态.当系统状态变量初值[x(0),y(0),z(0)]=[-0.01,-0.02,-0.02]时,系统的相轨迹如图1所示

图1 新型类Lorenz系统的相图

2 新型类Lorenz系统的混沌控制

根据文献[7]输入-状态线性化的方法,设系统状态(x,y,z)=(x1,x2,x3),对(1)式施加控制u,受控的系统方程变为：

(1)对应于新型类Lorenz受控系统的矢量场f和g分别为：

(2)检验能控性和对合条件

能控性检验：

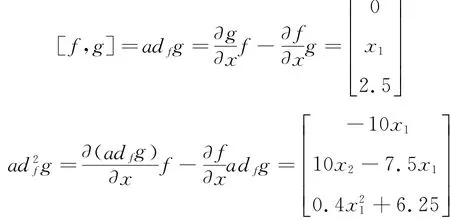
则C为满秩,则在R3内线性无关.

因为零向量是属于任何向量场的集合,故[g,adfg]构成一个对合集.

由(3)、(4)、(5)式可得

(4)计算Lfkλ(x),0≤k≤n-1,n=3

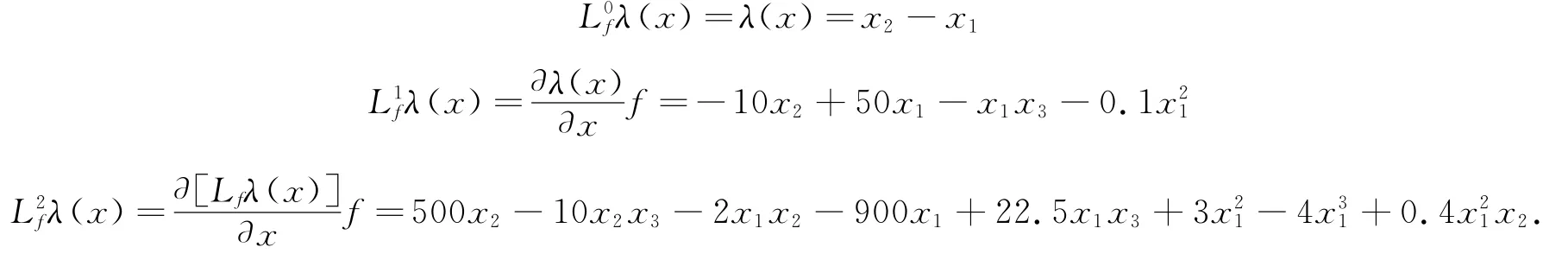
(5)求线性化状态方程及控制律u

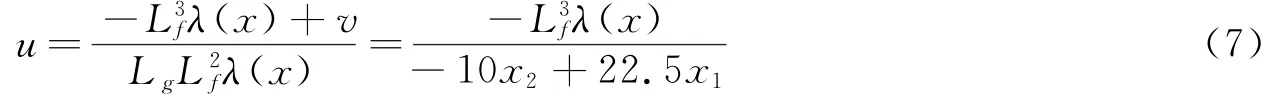
设z=[z1,z2,z3]T,则(8)式可写为：

其中,系统矩阵A和控制矩阵B分别为

这样便完成了输入-状态线性化,将用输入u去稳定原来的非线性动态系统式(2)的问题,转变为用新的输入v去稳定新的动态系统式(8)的问题.新的动态系统式(8)是线性和能控的,采用线性状态反馈控制律：

并适当选择反馈增益,就能对极点任意地进行配置.由线性控制理论可知,只要系统式(8)的所有极点均严格位于s左半平面,这个系统就是稳定的.在此把新系统的三个极点均配置在-1处.

(10)式代入(8)式可得：

|sI-A|=s3-s2k3-sk2-k1.而[s-(-1)]3=s3+3s2+3s+1,所以k1=-1,k2=-3,k3=-3.线性化后的系统的控制量v为：v=-z1-3z2-3z3.

由此可得(2)式的控制量u为：

3 仿真结果

系统初值取(x1(0),x2(0),x3(0))=(-0.01,-0.02,-0.02),仿真结果如图2～图5所示.

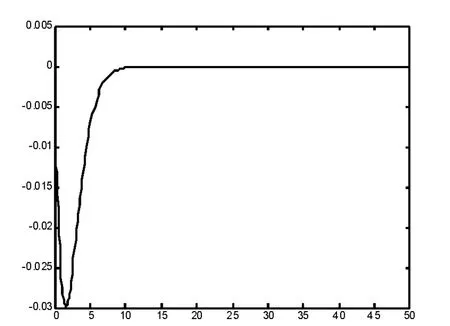
图2 受控系统x1的状态响应

图3 受控系统x2的状态响应

图4 受控系统x3的状态响应

图5 受控系统的相图

其中,图2为受控系统x1的状态响应,图3为受控系统x2的状态响应,图4为受控系统x3的状态响应,通过仿真可以看出：新型类Lorenz系统在施加控制式(12)后,系统的三个状态变量均在较短时间内稳定地收敛于原点.图5为受控系统的相图.

4 结 论

采用输入-状态线性化方法对新型类Lorenz混沌系统进行控制,使系统的三个状态变量稳定地收敛于零,从而消除了混沌.在一定条件下,输入-状态线性化方法可以将一个仿射非线性系统进行精确线性化(即没有模型误差),并且这个状态反馈可保证控制系统的稳定性,并有好的动态品质.

[1]G.Chen and X.Dong.From Chaos to Order：Perspectives and Methodologies in Controlling Chaotic Nonlinear Dynamical System[J].Int.J.Bifurcation and chaos.1993,3(6)：1363-1409.

[2]陈立群,刘延柱.控制理论的研究现状与展望[J].上海交通大学学报.1998,22(1)：108-114.

[3]T.Hartley,F.Mossayebi.A Classical Approach to Controlling the Lorenz Questions[J].Int.J.Bifur.chaos.1992,2 (4)：881-887.

[4]陈立群,刘延柱.一类非线性振子中混沌运动的反馈控制[J].上海交通大学学报.1997,31(1)：32-35.

[5]陈立群,戈新生.混沌的非线性控制[J].科技通报.1997,13(3)：156-158.

[6]王琳,倪樵,刘攀.一种新的类Loren系统的混沌行为与形成机制[J].动力学与控制学报,2005,3(4)：1-6.

[7]周群利,张绍德.基于反馈线性化的Duffing混沌系统控制[J].安徽工业大学学报,2007,24(1)：58-61

Study on the Control of a New Lorenz-like System

ZHOU Qunli
(School of Electrical Engineering,Wuhu Vocational and Technical College,Wuhu,Anhui 241006,China)

a new Lorenz-like system;input-state linearization;chaotic control

Input-state linearization is adopted to control a new Lorenz-like system.First,controllability and involutivity of the controlled system are tested.When the conditions for linearization are met,the nonlinear system model is transformed into a linear one by using the Lie derivative and Lie bracket operation in differential geometry.In this way,the control problem of nonlinear system is changed to the problem of the linear system.Then a linear state feedback control is designed for the linearized system.When the feedback gain are selected properly,the poles of the system can be arbitrarily configured.The chaos is eliminated when the three state variables of the system steadily converges to zero.The simulations proves the effectiveness of the method.

周群利,硕士,讲师,研究方向：非线性系统控制.

O157.1

A

1009-9506(2015)08-0044-05

2015年5月23日