量子体系扰动的能量本征值估计

李茂泉

(玉溪师范学院理学院,云南玉溪653100)

[物 理]

量子体系扰动的能量本征值估计

李茂泉

(玉溪师范学院理学院,云南玉溪653100)

量子体系;能量本征值;Hoffman and H.W.Wielandt定理

运用本征值的扰动处理这一现代数学方法讨论量子体系能量的本征值扰动问题,并将Hoffman and H.W.Wielandt定理作了推广.

量子微扰论对本征值进行扰动的处理以瑞利-薛定谔方法为基础,扰动可以获得较为精确的本征值.但是,由于精确的量子测量在实践中有难度,因此,实际需要解决的问题是：在扰动后如何估计本征值在一个区间内的分布情况,并为数值分析提供理论上的指导.有关这方面的工作,国内学者孙继广对其进行了研究,并取得一定的进展[1].但是,在量子体系方面,相关的研究却鲜有报道.

近年来,笔者研究了一个二维体系的能量扰动问题,并通过分析发现扰动的界限和范数联系密切,且本征值的扰动也可以通过算符的范数特征来进行分析.基于以上的认识,笔者对扰动的数值计算与模拟提供一个扰动的界限,并且通过数学上的分析,可以把有关定理做更为实用的推广.

因此,本文中,笔者在对原始模型分析和边界扰动进行分析的基础上,对Hoffman and H.W.Wielandt定理进行了推广.

1 原始模型与分析

考虑一个二维对称扰动的例子,系统原来为H0,扰动矩阵为H′,有扰动的矩阵由下述表述：

将H分解：

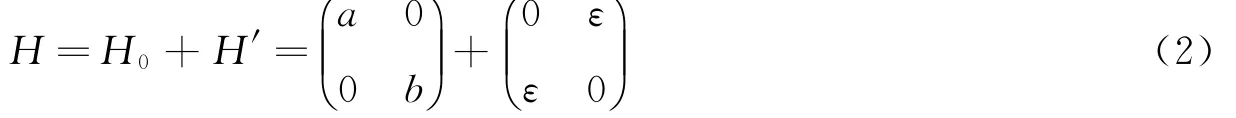
详细解H的本征值,结果是：

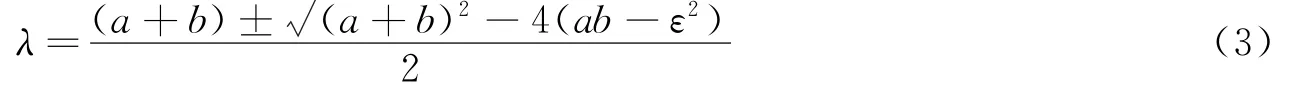
由于能量的实数特性,所以判别式应当大于等于0,为了和数值化计算比较,现使本征值有序.于是,本征值式子变为：

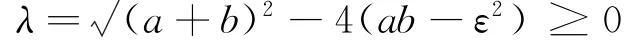
假设判别式大于0,所以,若本征值有序,必须有(a-b)2≥ε2.于是,获得两个有序的本征值：

按瑞利-薛定谔扰动处理,将本征值H0修正为：

上述分析只进行到2级修正,高级修正比上一级是小量,在实践中,通常可以忽略.

2 边界扰动分析

下面用扰动定理[1]分析.首先,算出H′的本征值：

λ的序列为：λmax=ε,λmin=-ε.

于是,能量E1′,E2′的修正区间为：

容易看出,(5)、(6)两式与上述结果是相容的,(7)、(8)两式对扰动的边界给出了限制,不仅限于2级微扰.由于‖H-H0‖F→0,当ε趋于零,H的本征值趋于未扰动的值,这说明扰动是稳定的(Ostrowski定理)[6],(7)、(8)两式给出了扰动的边界,这在数值计算中是很重要的,其对算法的设计有着直接的影响.

当然,通过分析H,H0的本征值问题也可获得这种估计,由文献[1,4]定理,可以在范数级别上完成这种分析.由Hoffman and H.W.Wielandt定理[4]知,算符H,H0的Euclid距离与算符自身的F范数关系为：分别是H,H0的本征值,计算

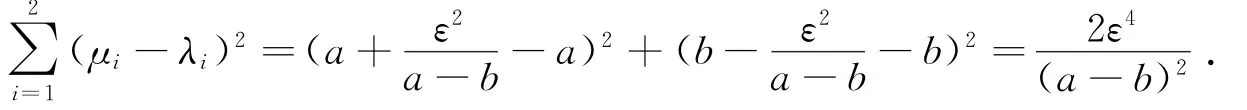
3 定理的推广

Hoffman and H.W.Wielandt定理虽然可以绕开扰动具体的形式对本征值进行计算,但还是要计算差值矩阵元,编程上仍然占用较多的内存,这样会导致系统运行速度变慢.因此,从矩阵元素本身出发来对扰动进行估计就成为了一个很现实的问题.而其实上,只要我们注意到范数的性质,由Minkowki不等式[2,3],立刻可以得到：

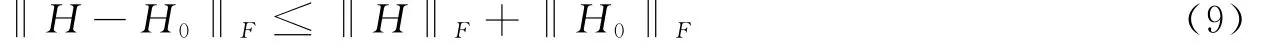
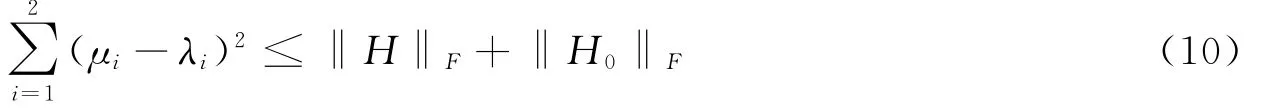
由此,从H,H0的F范数就可以完成对扰动矩阵的估计,这正是矩阵算法所需要的.至此,定理推广完成.

综上,笔者讨论了非对角元素对称小量对原本征值的扰动,这是量子体系中出现较多的一种情况.不过,限于篇幅,笔者对小参数直接对本征值的微扰没有讨论,也没有涉及非线性本征值的扰动问题,但用泛函讨论应当是合理的途径.另外,力学中的惯量主轴的扰动分析与此类似,对此笔者将另文讨论.

[1]孙继广.矩阵扰动分析[M].北京：科学出版社.2001：183-197.

[2]孙经先.非线性泛函及其应用[M].北京：科学出版社.2008：56-59.

[3]程其穰.实变函数与泛函分析基础[M].北京.高等教育出版社.1983：198-120.

[4]A.J.Hoffman and H.W.Wielandt,The variation of the spectrum of a normal matrix[J].Duke MATH.J.,1953 (20)：37-39.

[5]J.H.Wilkinson,he Algebraic Eigenvalue Problem[M].Clarendon Press,Oxford,England,1965.

[6]A.M.Ostrowski,Uber die Stetigkeit von charakteristischen Wurzeln in Abhanigkeit von den Matrizenelementen[J]. Jahresber.Deutch Math.-Verein.,1957(60)：40-42.

Estimation on Perturbed Energy Eigenvalues of the Quantum System

LI Maoquan
(School of Science,Yuxi Normal University,Yuxi,Yunnan 653100,China)

quantum system;energy eigenvalue;Hoffman and H.W.Wielandt theorem

The modern mathematical method of eigenvalue perturbation was used to analyze the perturbation problem of energy eigenvalues in quantum system and the promotion of Hoffman and H.W.Wielandt theorem was made in this paper.

李茂泉,副教授,研究方向：量子力学、物理学.

O59

A

1009-9506(2015)08-0041-03

2014年2月28日