不定积分∫csc xdx的解法研究①
2015-12-15张友梅
张友梅
(合肥职业技术学院基础部,安徽合肥238000)
不定积分∫csc xdx的解法研究①
张友梅
(合肥职业技术学院基础部,安徽合肥238000)
不定积分;余割函数;恒等变形;凑微分
通过对余割函数作不同的恒等变形,利用凑微分、换元等方法得到不定积分∫csc xd x的多种解法.不定积分的求解具有方法灵活性大、技巧性强等特点,而通过对不定积分多种求解方法的练习,不仅可以选择出问题简洁的求解方法,同时有效地培养了学生的灵活性和创造性. [作者简介]张友梅,硕士,讲师,研究方向:泛函微分方程及数学教育教学.
不定积分的计算是高等数学教学的重点和难点,其求解方法灵活性大,技巧性强,而且同一个不定积分往往有多种不同的求解方法[1].例如,对于不定积分∫csc xdx的求解,很多高等数学教材都给出不同的
解法,如教材[2~4]都给出两种不同的解法.实际上,不定积分∫csc xd x还有一些更为简便的解法,当然也有一些解法是较为复杂的.对此,本文通过对余割函数作不同的恒等变形,利用凑微分、换元等方法对不定积分∫csc xdx的多种解法进行分析和求解,目的是培养学生的灵活性与创造性.
例 求不定积分∫csc xdx
分析 显然∫,csc xdx不能直接用基本积分公式来求解,且被积函数结构简单,这给求积分带来一定的困难.但是,考虑到余割函数属于三角函数,而三角函数有诸多的恒等变形公式,这就给解题打开了广阔的思路.通过对余割函数csc x作不同的恒等变形,利用凑微分、换元等方法,我们可以得到不定积分∫csc xdx的多种解法.
思路一 利用倒数关系sin x csc x=1和倍角公式,对余割函数csc x进行恒等变形,满足凑微分,再运用基本积分公式解题.
解法一
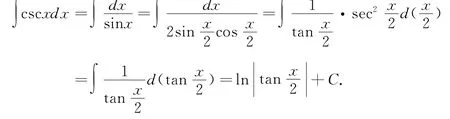
解法二
这是一种最常见的解法,大多数教材都采取这种解法.
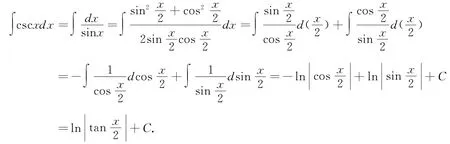
思路三 对余割函数分子分母同乘以函数csc x-cot x,直接凑微分解题.
解法三

思路四 利用倒数关系sin x csc x=1和平方关系sin2x=1-cos2x对余割函数csc x进行恒等变形,再凑微分求解.
解法四
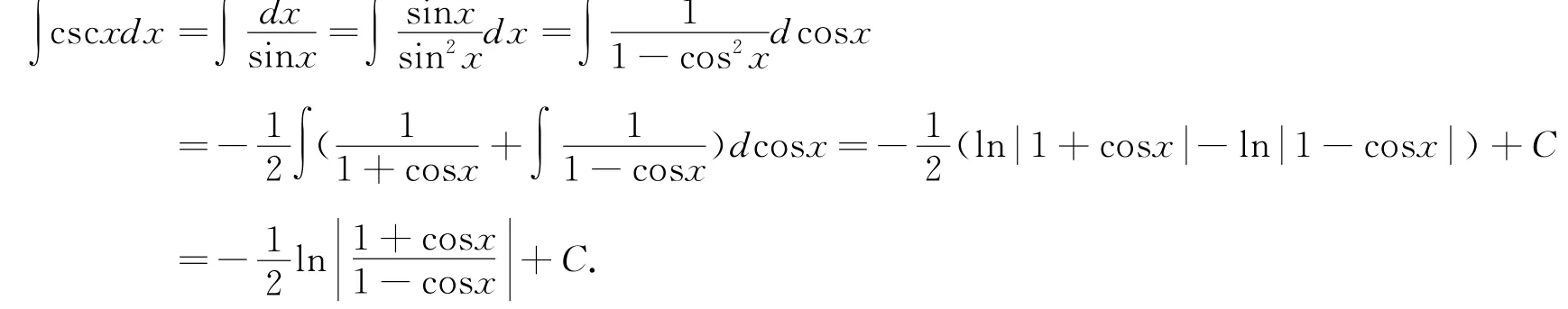
解法五
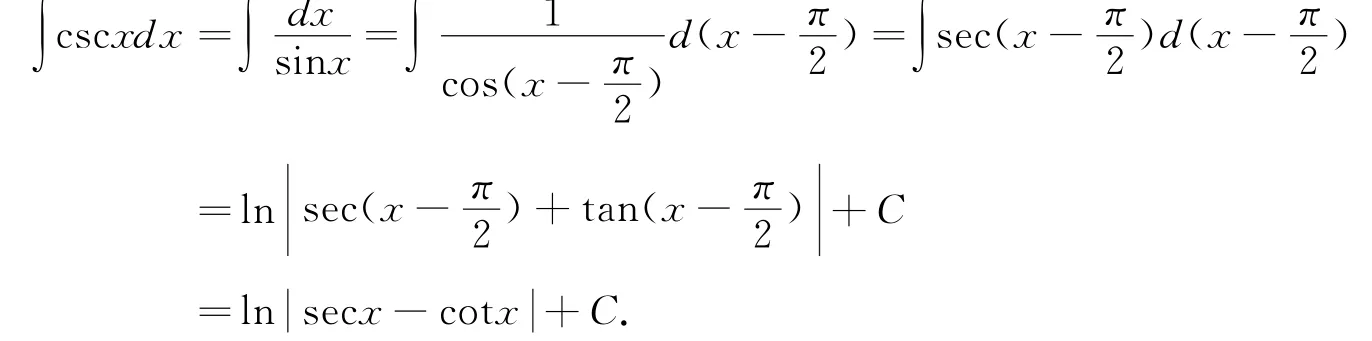
思路六 数学的各部分之间是相互联系、相互渗透的,例如解方程组和求不定积分就有一定的内在联系,对于某些不定积分,可以通过构造方程组来求解,而且能够降低求解的难度[5].本题根据所求积分的特点,可构造另一积分,联立方程组求解.

思路七 当被积函数是三角函数时有理式时,其积分总是可以使用万能代换进行换元,将被积函数由三角函数转化成有理函数,再根据有理函数的积分法求出其解[6].
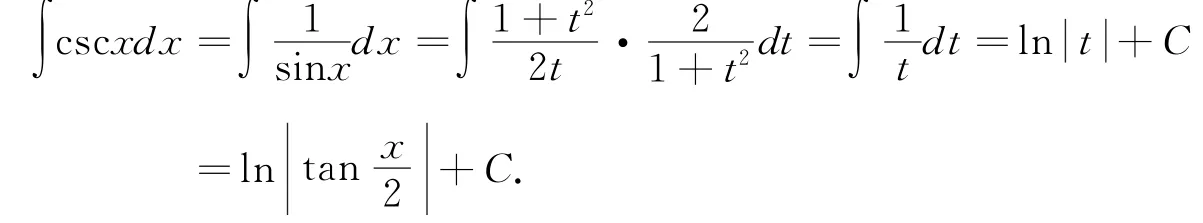
思路八 换元是求不定积分的最常用最重要的方法,本题亦可通过多次换元求解.
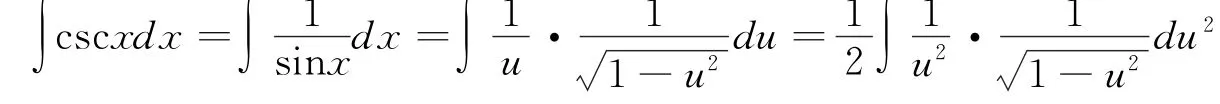

思路九 利用公式1=cot x tan x,尝试用分部积分法解题.
解法九

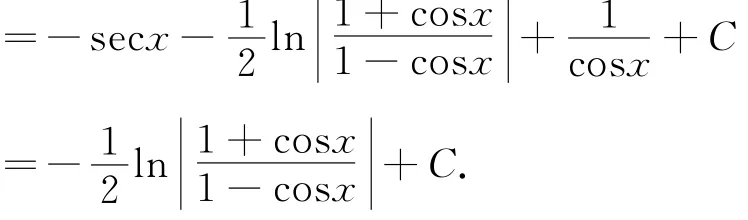
比较而言,解法三形式上最为简洁,但思维上不易想到,解法一与解法七是最常见的解法,也是较好的解法,而解法八与解法九都较为复杂.由此可见,不定积分的解法是灵活多变的,其结果在形式上也不尽相同,但利用三角恒等式化简,本题结果中的四种不同形式均是一致的.通过一题多解的训练,不仅可以选择出问题简洁的求解方法,同时有效地培养了学生的灵活性和创造性.
[1]吴维峰.对不定积分一题多解的分析[J].高等数学研究,2010,13(6):11-13.
[2]高汝熹.高等数学:(一):微积分[M].武汉:武汉大学出版社,1998:234-235.
[3]柳重堪.高等数学:上册:第一分册[M].北京:中央广播电视大学出版社,2002:260.
[4]同济大学等编.高等数学[M].北京:高等教育出版社,2003:229.
[5]毛北行,李新芳.方程组解法在求不定积分中的应用[J].河南机电高等专科学校学报,2013,21(6):99-100.
[6]胡静波.高等数学的发散思维培养研究[J].湖北科技学院学报,2013,33(12):29-30
The Solution to Indefinite Integral∫csc xdx
ZHANG Youme
(Department of Basic Courses,Hefei Vocational&Technical College,Hefei,Anhui,238000,China)
indefinite integral;cosecant function;identical deformation;improvising differentiation
The solution to indefinite integral∫csc xdx is obtained by using various methods such as improvising differentiation and variable change through different identical deformation of cosecant function.Practice with various solving methods of indefinite integral can help students choose a simple one and cultivate their flexibility and creativity.
O157.1
A
1009-9506(2015)08-0035-04
2015年4月27日
安徽高校省级质量工程项目《高等数学》精品课程,编号:2013gxk161;合肥职业技术学院质量工程项目《高等数学》精品课程,编号:JPKC201302.
