@Risk软件绘制成本-效果可接受曲线过程解析

刘 思 胡 霞 余 正

@Risk软件绘制成本-效果可接受曲线过程解析

刘 思 胡 霞 余 正

成本-效果可接受曲线（CEAC）是药物经济学中常用的反映成本-效果不确定性分析结果的曲线。已有文献多集中在对其原理的研究，而介绍绘制该曲线过程的文献几乎没有。本文旨在通过@Risk软件来解析CEAC的绘制过程，用一种简单易懂的方式帮助药物经济学的初学者理解CEAC的原理以及相关的敏感性分析的知识。

@Risk软件；成本-效果可接受曲线；绘制

成本-效果分析（CEA）是药物经济学评价中使用最为广泛的分析方法，由于数据和假设的不确定，这种分析方法存在着许多不确定性。概率敏感性分析（PSA）是处理这种不确定性的常用方法。成本-效果可接受曲线（CEAC）能够直观地描述PSA的结果。在已发表的国内文献中，对 CEAC的研究较少。吴晶和刘国恩[1]对CEAC的计算方法进行了介绍，但并未详述具体的绘制过程；宗欣和孙利华[2]从理论上分析了 CEAC与成本-效果阈值的关联性；彭娟和骆福添[3]探讨了在多元贝叶斯回归模型框架下绘制 CEAC的方法，在绘制的过程中需要借助于R软件进行编程，再在Openbugs软件中实现模拟。可见，现有对 CEAC的研究以理论为主；仅有个别文献介绍了CEAC的绘制方法，而这种绘制方法需要有一定的软件编程基础。本文介绍了在Microsoft Excel中，运用@Risk软件绘制CEAC的过程。主要是以一种简单易懂的方式，使成本-效果不确定性分析的初学者对CEAC的绘制过程有一个较为直观的认识，从而加深对 CEAC原理的理解。

1 CEAC的原理

概率敏感性分析大多建立在Monte Carlo模拟模型基础上，人为地选取一些总体，根据预定的分布来检验所有变量在可能范围内同时变化对评价结果的影响。基于Monte Carlo模拟的PSA是最常用的处理模型中不确定性的方法。中国药物经济学评价指南（2011版）[4]建议在参数较多和模型设计时采用Monte Carlo模拟进行PSA。CEAC反映的是基于二阶 Monte Carlo模拟的 PSA的结果。二阶Monte Carlo模拟的基本原理为：①假设模型中的参数为随机变量，给每一个输入变量确定一个概率分布，从这些分布中为每一个输入变量随机抽取一个值，计算成本和效果，即完成一次模拟；②多次重复抽样和计算，从而产生大量的成本和效果估计值（可以得出置信区间）；③应用这些估计值构造一个联合分布，展现不同干预措施的成本和效果的差异，此处便可以用CEAC来反映。

采用净效益法可以得到以Monte Carlo模拟为基础的CEAC。计算公式为：

其中W为单位效果的意愿支付；NB（W）为意愿支付为W时的货币净效益值；△C和△E分别是两种方案相比较后的增量成本和增量效果；CE（W）为意愿支付为W时，货币净收益值大于零的概率。CEAC反映了公式（2）中W与CE的关系，以W为横坐标、CE为纵坐标。

2 @Risk分析软件的简介

@Risk是Palisade公司制造的风险与决策分析软件。它是Microsoft Excel的一个插件，使用MonteCarlo模拟进行风险分析，在Microsoft Excel电子表格中显示众多可能结果及其发生率。通过@Risk可以方便地定义分布函数，其内置的概率分布函数包括正态分布、均匀分布、三角分布等37个。@Risk与电子表格完全集成，浏览、定义和分析全部在Excel表格中完成，可以在熟悉的环境中进行风险和不确定性分析。同时，该软件与Palisade公司制造的另一种风险与决策分析工具套件DecisionTools Suite中的所有程序完全兼容，可以相互结合以进行更深入的剖析和分析。@Risk软件现已被广泛应用于金融、医药、环境等不同的行业中。

@Risk作为Microsoft Excel的一个插件，菜单界面见图 1。运用该软件进行不确定性分析时，一般分6个步骤：①开发模型逻辑；②指定@Risk输出项；③定义输入项分布；④设置迭代次数；⑤运行模拟；⑥分析结果。

3 示例

以下用一个实例来演示运用@Risk软件绘制CEAC的过程。假设两种药物治疗同一种疾病，即A药和B药。对这两种药物进行增量成本-效果分析，比较二者的经济性，以CEAC来反映分析结果。从表1数据来看，A、B两药物治疗的人均成本C和治疗的有效率ε为不确定性参数。首先，使用@Risk软件进行Monte Carlo模拟，根据这两个不确定性参数的假设分布及范围生成绘制CEAC所需的模拟数据；然后，利用Microsoft Excel自带的计算功能和逻辑函数计算出已设定的每一个意愿支付值所对应的“具有成本-效果”的概率（%CE），并绘制CEAC。

3.1 运用@Risk生成模拟数据

3.1.1 开发模型逻辑 根据表1中的数据，在安装了@Risk插件的Excel表格中列出已知输入项、不确定的输入项及其分布和参数范围，并计算输出项，见图2。输出项中，增量成本的计算公式为：△C=N×（CACB）；增量效果的计算公式为：△E=N×（EA－EB）。

图1 @Risk软件的菜单界面

表1 两种药物的成本-效果参数

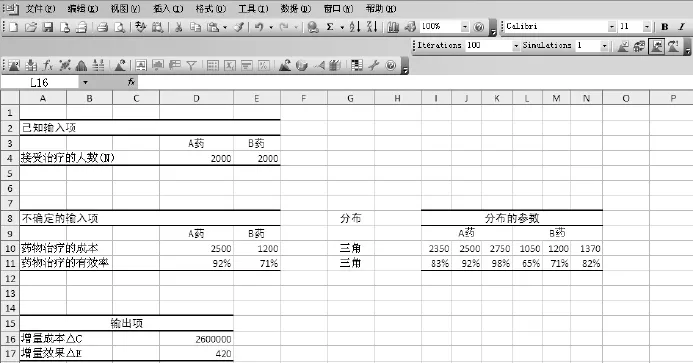
图2 模型逻辑

3.1.2 指定@Risk输出项 将光标放在需要指定的输出项数据单元格上（此处对应的2 600 000和420两个单元格），点击菜单上的“添加输出项”按钮，指定@Risk输出项，见图3。在弹出的对话框中设定输出项的名称，该名称将会显示在之后的报告中。设定完成后，△C和△E两个输出项的表达式变成了“=RiskOutput（"增量成本△C"）+E4 ×E10－F4×F10”和“=RiskOutput（"增量效果△E"）+E4×E11－F4×F11”，表示其已是@Risk的输出项。

3.1.3 定义输入项分布 将光标放在不确定输入项的数据单元格上（此处对应的2 500、1 200、92%和71%这4个单元格），点击菜单上的“定义分布”按钮，定义不确定性参数的分布，见图4。

图3 指定@Risk输出项

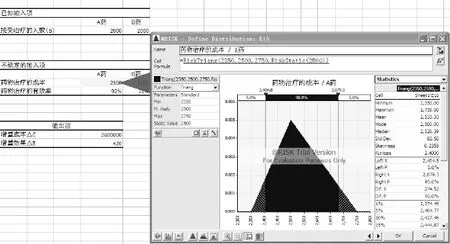
图4 定义CA的分布

表1中列出的A、B两种药物的成本和有效率都服从三角分布，所以CA、CB、EA、EB4个参数的分布表达式分别为：

3.1.4 设置迭代次数并运行模拟 在菜单的“迭代”栏中选择1 000，即迭代1 000次，会得到1 000组△C和△E的模拟数据。点击“开始模拟”按钮运行模拟，模拟状态见图5。

3.1.5 结果 模拟结束后，单击菜单上的“Excel 报表”，在弹出的菜单中勾选“Simulation Data”，然后单击“OK”，便可将这1 000组模拟数据以Excel表格的形式导出来，见图6～7。其中，图7是人工删除了中间的994组数据后的简化形式。

图5 运行模拟状态

图6 导出模拟数据

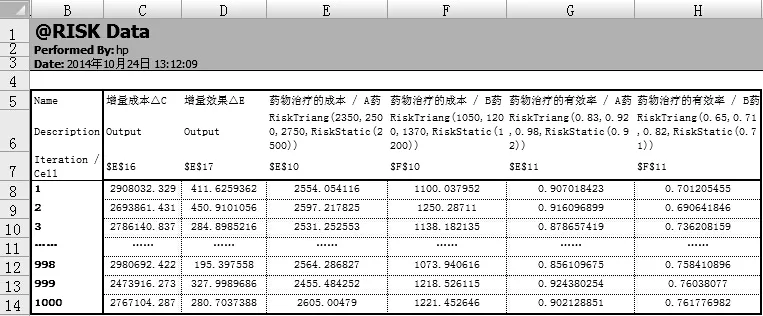
图7 Excel报表—模拟数据

3.2 在Microsoft Excel表格中绘制CEAC

3.2.1 设定意愿支付值 若A药比B药更具成本-效果，则净效益值 NB（W）=W×△E－△C＞0，即意味着W＞△C/△E。此处，与B药相比，A药更具成本-效果的概率即为在这1 000组模拟数据中，W＞△C/△E的概率。既然需要将W与△C/△E进行比较，则可以根据已模拟出的△C和△E的数值来计算对应的△C/△E，得出大致范围，据以设定需要进行分析的W值。本例研究中，利用Excel自带的计算功能，计算出已生成的1 000组模拟数据对应的1 000个△C/△E值，其中，最小值为3 938.51，最大值为3 2703.78，故设定W的范围为（3 000，33 000），每个值的间隔为1 000，见表2中第一行黑色部分。

3.2.2 设定逻辑函数进行计算 设定好意愿支付值后，就需要计算每一个意愿支付值满足 W×△E－△C＞0的概率。在Excel表格中，可以通过IF函数来计算每一个W与每一组模拟数据的比较结果。以表2中加粗的单元格为例，其逻辑运算函数为：IF（M7×$D$8－$C$8＞0，1，0），其中，M7对应着W=3 000，D8、C8分别对应着图7中的模拟数据。如果M7×$D$8－$C$8＞0成立，则单元格中显示1；若不成立，则显示0。所以，通过Excel的计算，“1”代表“W×△E－△C＞0”，即A药比B药更具成本-效果。将光标从该单元格横向拖动，可以得出所有意愿支付值与第一组模拟数据相比的结果；将IF（M7×$D$8－$C$8＞0，1，0）改为IF（$M$7 ×D8－C8＞0，1，0），将光标纵向拖动，可以得出第一个意愿支付值“3 000”与这1 000组模拟数据相比较的结果，显然都为 0。如此反复，即可计算出所有意愿支付值与这1 000组模拟数据相比较的结果，见图8。

图8 意愿支付值W与模拟数据的比较

3.2.3 汇总并调整意愿支付值 对于每一个意愿支付值W，其通过IF函数与每一组模拟数据比较后得到的结果只有两种：1或0。“1”代表在该W值下，A药比B药更具成本-效果；“0”代表在该W值下，A药并不比B药更具有成本-效果。所以，将每一W值对应的1 000个逻辑运算值求和，再除以1 000，即为在该意愿支付值下，A药比B药更具有成本-效果的概率（%CE），如图8中的最后两行。从图8中可以看出，5 000和6 000这两个W值对应的%CE分别是0.048和0.231，这两个值间隔太大。为了使分析结果更为精确，需要调整之前所设定的W值。此处在5 000和6 000这两个W值中间插入5 300和5 600，按上述相同方法分别计算得到0.09和0.137这两个概率值。

3.2.4 作图并分析结果 以W为横坐标、%CE为纵坐标，做XY散点图，即得到CEAC，见图9。图中，点（6 000，0.231）表示当单位效果的意愿支付为6 000元时，A药比B药更具有成本-效果的概率是23.1%；点（9 500，0.813）表示当单位效果的意愿支付为9 500元时，A药比B药更具有成本-效 果的概率是81.3%。

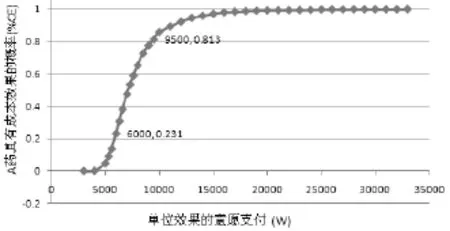
图9 成本效果可接受曲线CEAC

4 讨论

本文在回顾了CEAC原理的基础上，用一种简单易懂的方式演示了如何利用@Risk软件生成Monte Carlo模拟数据，继而在Excel表格中通过各种逻辑和函数运算绘制出CEAC。整个过程需要操作者在充分理解的基础上一步一步手动完成，可以让初学者对Monte Carlo模拟和CEAC的原理有一个更为深刻和直观的认识。而在真正进行药物经济学的概率敏感性分析时，通过TreeAge软件即可以很方便地得到CEAC，省去了中间的计算环节。所以，并不推荐在实际的应用中使用本方法绘制CEAC，本文主要是为初学者理解CEAC的原理及相关概率敏感性分析的知识提供参考借鉴。

[1]吴晶,刘国恩.成本-效果可接受曲线:不确定状态下的医疗决策方法[J].中国药物经济学,2006,1(3):55-59.

[2]宗欣,孙利华.成本效果可接受曲线与成本效果阈值[J].中国新药杂志,2012,22(19):2222-2225,2296.

[3]彭娟,骆福添.多元贝叶斯回归模型框架下绘制成本-效果可接受曲线[J].中国药房,2013,24(10):865-867.

[4]《中国药物经济学评价指南》课题组.中国药物经济学评价指南(2011版)[S]北京,2011.

The Process Analysis of drawing Cost-Effectiveness Acceptable Curve by @Risk software

Liu Si Hu Xia Yu Zheng

Cost-Effectiveness Acceptable Curve(CEAC)is frequently used in Cost-Effectiveness uncertainty analysis in PE.Most related article focused on the research of its theory.Whereas,there were almost no article introduced that curve’s drawing process.This Article analysed the CEAC’s drawing process by @Risk software,aimed to using a straightforward way to help the PE’s beginners to understand the theory and related sensitivity analysis knowledge of the CEAC.

@Risk software;Cost-Effectiveness Acceptable Curve;Draw

中国药科大学国际医药商学院，江苏南京 211198

余正，E-mail：yzhengu@aliyun.com

R-05

A

1673-5846(2015)05-0008-05