基于局域均值分解和BP神经网络的大坝变形预测

董正坤，罗亦泳，蒋斯斯，臧德彦，张立亭，谢翠贞

（1.东华理工大学 测绘工程学院，江西 南昌330013；2.东华理工大学 江西省数字国土重点实验室，江西 南昌330013；3.江西省测绘地理信息局，江西 南昌330013；4.南京师范大学 虚拟地理环境教育部重点实验室，江苏 南京210046）

大坝变形预测受诸多的因素影响，监测过程中主要考虑水位、温度及时效等影响因素。这些因素往往具有非线性特征，对大坝做出准确的预报十分困难。由此多项式曲线拟合、遗传算法、BP神经网络、支持向量机等模型在大坝变形预测中得到广泛的应用［1-4］。最近，Jonathan S.Smith在总结前人研究的基础上，提出一种新的自适应非平稳信号的处理方法—局部均值分解。它可以自适应地将复杂的非平稳信号分解成若干个，具有物理意义的PF分量之和［5］。有学者研究和比较了经验模式分解（EMD）和LMD，结果显示，在仿真信号分析中LMD方法优于EMD方法［6-8］。因此，本文利用LMD来分解变形大坝位移数据。BP神经网络方法已经广泛地应用于参数识别、故障诊断、负荷预测和大坝位移变形预报中［9-12］。本文针对提高BP神经网络对大坝变形监测的预测能力，根据丰满大坝变形观测数据，探讨并建立基于局域均值分解和BP神经网络的构建模型，分别利用局域均值分解和BP神经网络进行回归预测，建立多层次、多尺度预测模型，进一步提高大坝变形预测精度，为大坝安全预报和管理决策机构提供更高质量的预报信息。

1 研究方法

1.1 局域均值分解

LMD可自适应地将复杂的信号分解为若干个具有非负性和物理意义的PF分量之和，其中每一个PF分量由一个包络信号和一个纯调频信号相乘而得到。并且，包络信号是该PF分量的瞬时幅值，而PF分量的瞬时频率则可由纯调频信号直接求出。进一步将所有PF分量的瞬时频率和瞬时幅值组合，便可以得到完整的原始信号时频分布。对于任意信号，其分解过程［13］：

1）寻求局部均值函数m11（t）和局部包络函数a11（t）。设任意两相邻极值点为ni和ni＋1，则有

采用滑动平均法对局部包络函数进行平滑。如果相邻点的值是相等的，将继续滑动直至所有的相邻点不再相等，得出局部包络函数m11（t）和a11（t）。

2）将局部均值函数m11（t）从原始信号x（t）中分离出来，得到

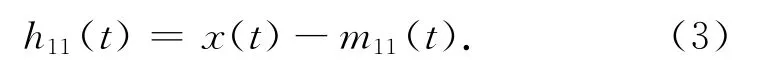
对h11（t）进行解调

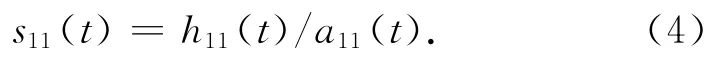
理论上，s11（t）是一个纯调频信号，即它的局部包络函数满足a12（t）＝1。如果a12（t）≠1，那么将重复以上程序直至s1n（t）变为纯调频函数，也即s1n（t）的包络估计函数a1（n＋1）（t）＝1。

3）求出包络信号的PF分量。在迭代过程中产生的所有包络估计函数相乘便可得到包络信号a1（t），

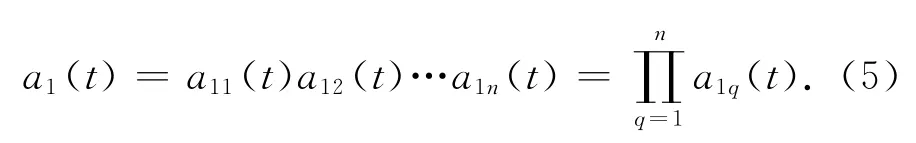
4）得到原始信号中的第一个PF1分量。将包络信号a1（t）和纯调频信号s1n（t）相乘得到PF1

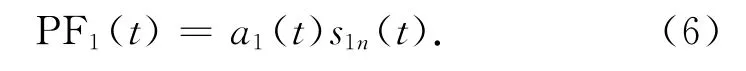
5）将PF1（t）从原始信号x（t）中分离出来，得到一个新的信号u1（t），

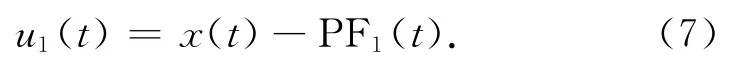
把u1（t）作为一个新的信号，将u1（t）作为原始数据重复以上步骤，循环k次，直到uk（t）为一个单调函数为止。因此，原始信号能被k个PF分量和uk（t）重构，即

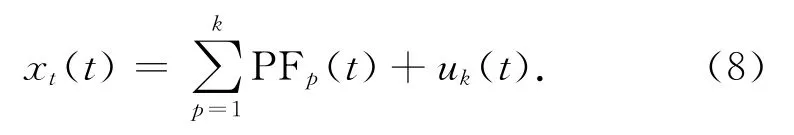
综上所述，这是一个消除高频分量信号渐进的过程，并且没有造成原始信号的损失。

1.2 局域均值分解和BP神经网络的预测模型

设大坝在不同时间段的位移值作为一列时间序列｛X（t），t＝1，2，…，n｝，对该序列数据进行局域均值分解，对分解PF分量进行BP神经网络方法进行预测，再将各PF分量进行合成，对大坝变形预测值进行重构［12，14］，见图1。

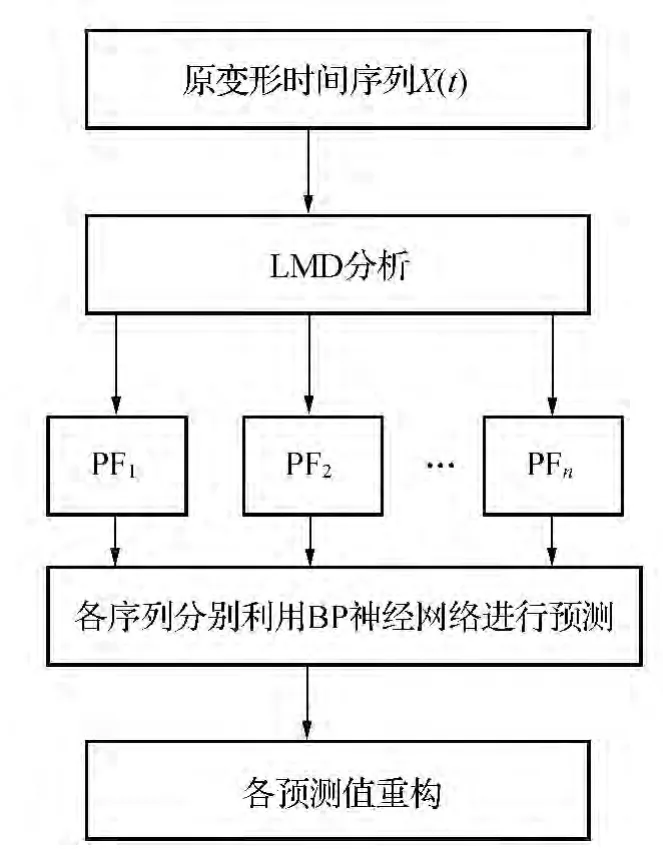
图1 LMD-BP预测模型结构

为了评价模型的预测性能，采用如下统计量对模型的预测效果进行评估：平均绝对百分比误差其中，Xt≠0；均方根误差平均绝对误差其中，Xt为实测值，t为预测值。

2 工程实例

2.1 实 例

根据丰满大坝30号坝段1985年1月～1990年6月期间的实测数据，利用局域均值分解和BP神经网络建立的模型对大坝进行变形预测，并用多项式曲线拟合预测模型进行对比分析。该测点共有61期观测数据，取前50组数据建模，后11组数据用于预测。

为降低建模误差，对BP神经网络的输入数据和输出数据进行归一化处理，使得输入值介于［-1，1］，而输出值介于［0，1］。在BP神经网络预测阶段，需要对数据网络的输出进行反归一化处理。对预处理时间序列｛X（t），t＝1，2，…，n｝数据进行局域均值分解，可得原始数据及其分解后的各个分量如图2所示。

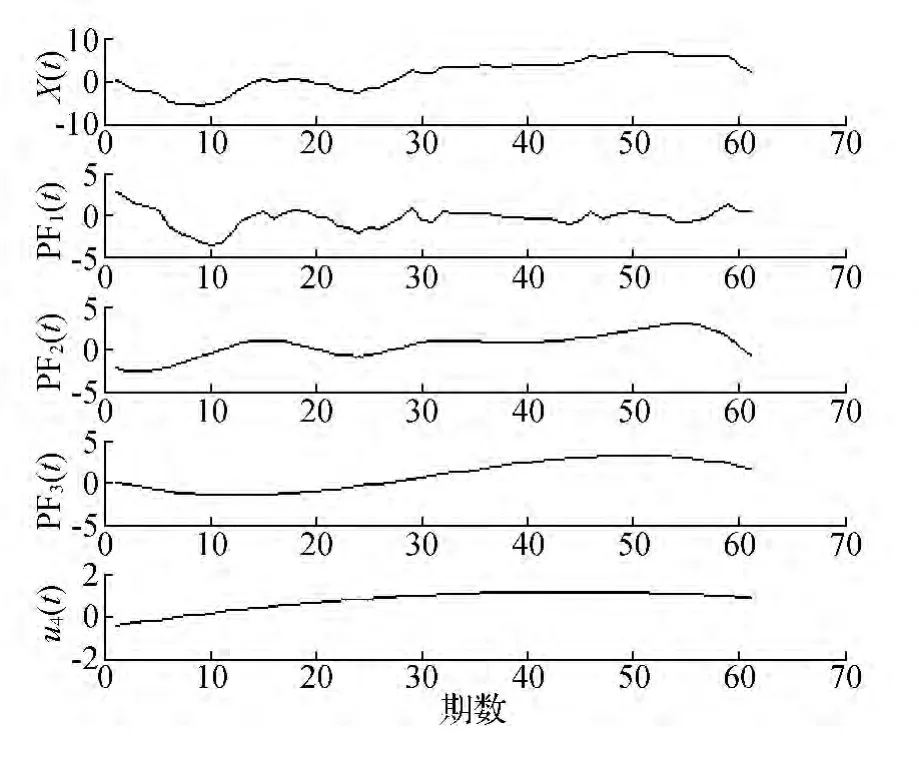
图2 原始观测序列及各个分解分量

对于61组观测数据利用LMD分解后得到4个PF分量，各个PF分量由影响大坝因素的水位、温度及时效等决定。由图2可知，水位H为主要影响PF1（t）的因素，影响大坝变形的高频信号；受温度T的影响，PF2（t）分量具有滞后性；而PF3（t）和u4（t）受由时效性影响［15］。

分解后，大坝变形监测观测数据共包含了4个生产函数。对这4个生产函数分别通过BP神经网络进行预测，从而得到51～61期的预测结果，见图3。

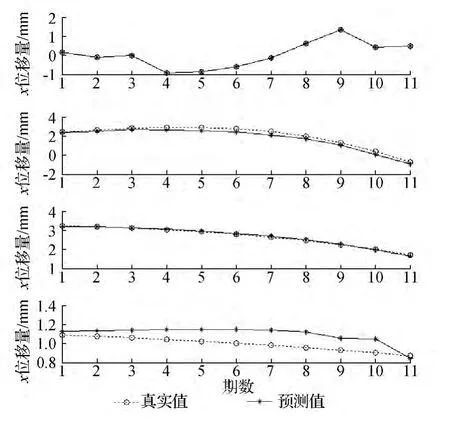
图3 各分量的预测值

由图3分析可得，其中各分量预测值PF1（t），PF2（t），PF3（t）和u4（t）的均方根误差RMSe分别为0.004 3、0.270 7、0.032 2和0.117 6mm。各个预测分量精度指标相对较高，为预测值重构提供较好的数据基础。

根据LMD-BP预测模型，即对分解后各PF分量进行BP神经网络方法进行预测，之后将各PF分量进行合成，对大坝变形预测值进行重构，最终得到变形时间序列的预测结果，如图4所示。

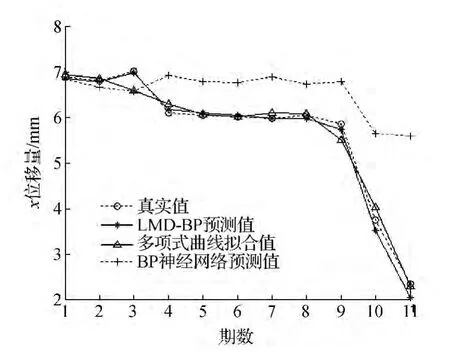
图4 大坝水平位移观测值与预测值对比

为说明LMD-BP模型的预测优越性，建立多项式曲线拟合预测模型进行预测实验［16］，由图4可得，各个模型精度指标的计算结果见表1。

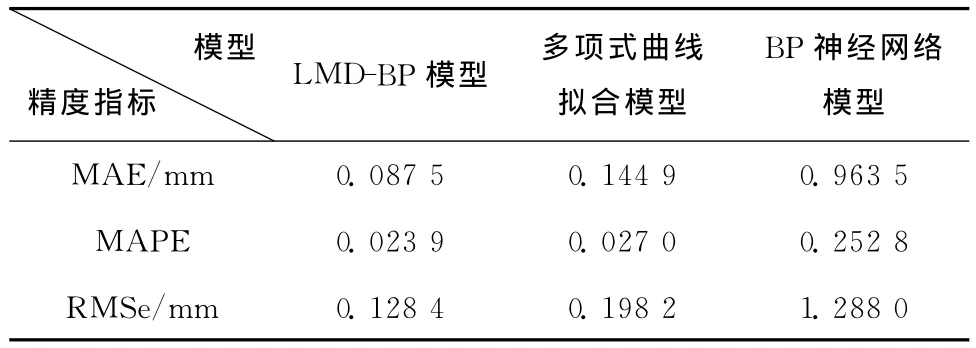
表1 三种模型精度评价指标比较

由表1可以看出，LMD-BP模型中，其平均绝对误差MAE为0.087 5mm，精度高于多项式曲线拟合模型和BP神经网络模型中的平均绝对误差。同理，LMD-BP模型中平均绝对百分比误差MAPE与均方根误差RMSe分别为0.023 9和0.128 4mm较高于多项式曲线拟合与BP神经网络模型中精度指标。因此，LMD-BP模型的精度明显高于传统的多项式曲线拟合模型以及单独运用BP神经网络模型，表明LMD-BP模型可以更好的应用于大坝的变形预测，并且有一定的可信度。

3 结束语

综合以上方法与结果，得出以下几点结论：

1）LMD是一种较新的非平稳信号处理方法，能自适应地将一个复杂的非平稳信号分解成多个具有物理意义的PF分量。

2）本文采用LMD-BP模型对丰满大坝30号坝段的实测数据进行有效预测，即先对该序列数据进行局域均值分解，对分解后各PF分量进行BP神经网络方法进行预测，再将各PF分量进行合成，最后对大坝变形预测值进行重构，在预测中获得良好的预测效果。

3）研究结果表明，与多项式曲线拟合模型相比，LMD-BP模型具有较高的运算精度和预测分析精度。因此，基于局域均值分解和BP神经网络模型在大坝变形预测中具有广泛的应用前景。

［1］沈月千，李威，黄腾，等.大坝变形分析周期均线系统模型的应用研究［J］.测绘工程，2014，23（3）：55-58.

［2］曹茂森，任青文，毛伟兵.基于解耦子波和优化神经网络的大坝变形预测［J］.岩石力学与工程学报，2005，24（10）：1751-1757.

［3］王新洲，范千，许承权，等.基于小波变换和支持向量机的大坝变形预测［J］.武汉大学学报：信息科学版，2008，33（5）：469-507.

［4］钟婷，杨敏华.多项式曲线拟合振荡现象的抑制［J］.湘潭师范学院学报，1999，20（6）：20-24.

［5］SMITH J S.The Local Mean Decomposition and its Application to EEG Perception Data［J］.Journal of the Royal Society Interface，2005，2：443-454.

［6］WANG Y，HE Z，ZI Y.A demodulation method based on improved local mean decomposition and its application in rub-impact fault diagnosis［J］.Measurement Science and Technology，2009，20（2）：1-10.

［7］WANG Y，HE Z，ZI Y.A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health diagnosis［J］.Journal of Vibration and Acoustics，2010，132（2）：1-10.

［8］程军圣，张亢，杨宇，等.局部均值分解与经验模式分解的对比研究［J］.振动与冲击，2009，28（5）：13-16.

［9］李守巨，刘迎曦，张正平，等.基于神经网络的混凝土大坝弹性参数识别方法［J］.大连理工大学学报，2000，40（5）：531-535.

［10］霍志红，张志学，郭江，等.基于神经网络的故障诊断研究［J］.工业控制计算机，2001，14（10）：19-21.

［11］代林.基于神经网络的电力负荷预测方法研究及实现［D］.成都：电子科技大学，2012.

［12］谢国权，戚蓝，曾新华.基于小波和神经网络拱坝变形预测的组合模型研究［J］.武汉大学学报：工学版，2006，39（2）：16-19.

［13］CHENG Junsheng，SH Meili，YANG Yu，YANG Lixiang.A roller bearing fault diagnosis method based on improved LMD and SVM［J］.Journal of measurement science and instrumentation，2011；2（1）：1-5.

［14］于伟，蔡璟珞，安凤平.边坡位移LMD-BP神经网络模型研究［J］.计算机应用与软件，2013，30（9）：107-109.

［15］张豪，许四法.基于经验模态分解和遗传支持向量机的多尺度变形预测［J］.岩石力学与工程学报，2011，30（2）：3681-3688.

［16］张帆，胡伍生.遗传神经网络在大坝安全评价中的应用［J］.测绘工程，2014，23（7）：41-45.