基于RTK的船载电子罗盘现场标定方法研究

2015-12-14宁振国岳建平

测绘工程 2015年4期

宁振国，岳建平，王雪

（河海大学地球科学与工程学院，江苏南京210098）

便携式遥控测量船按既定的航线进行测量，为了减少人工干预，需要获得较为精确的定位数据及航向数据。定位数据可通过RTK测量精确获得，而航向数据依赖于电子罗盘。但电子罗盘与RTK又分属不同的坐标系统，因此需要对电子罗盘的方向值进行标定，即求取电子罗盘各方向的补偿值。考虑到由于电子罗盘对其所处环境中的磁场较为敏感，若所处环境产生变化，则电子罗盘的补偿值也会随之改变，因此需要对电子罗盘进行现场标定。

电子罗盘精确标定的常规方法为：将电子罗盘在已知方位的标定装置上旋转一周，同时对其补偿值进行采样，最终拟合得到电子罗盘的补偿曲线。该方法只针对单独的电子罗盘，而未考虑到电子罗盘附着的装置对其补偿值的影响，并且该方法中的采样过程需要人工操作，不能实现自动标定。为此，本文提出一种针对便携式遥控测量船的电子罗盘自动标定方法，并通过实例对该方法进行分析。

1 电子罗盘补偿原理

电子罗盘的测量误差包括硬件误差和环境误差，硬件误差是由电子罗盘的制造工艺决定的，可以通过传感器本身自动补偿；环境误差包括安装误差和罗差，需要在使用前对电子罗盘进行标定，使用时对测量值进行补偿。

电子罗盘受到地磁力、硬铁磁力和软铁磁力的同时作用。硬铁磁力来源于永久磁铁或被磁化的金属。该补偿值与罗盘的相对方向值的关系为

式中：φ为罗盘的方向值；Δφ1为罗盘在当前方向的罗差；B，C为硬磁罗差补偿系数。

软铁干扰来源于地球磁场和罗盘附近磁性材料之间的相互作用，其干扰程度与罗盘的方向有关。该补偿值与罗盘相对方向值的关系为

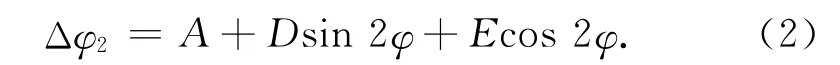
式中：Δφ2为罗盘在当前方向的罗差；A，D，E为软磁罗差补偿系数。

综上所述，针对测量过程中使用的工程坐标系，其方位值α与电子罗盘测量的方位值φ之间的关系为

其中

自古以来，山东盛产魁梧高大的汉子。巩晓彬之外，球队的主力中锋纪民尚也是当时国家队的常客。与巩晓彬不同，纪民尚以精准中投和踏实作风著称，从青年时便有了“老黄牛”的外号。再加上多次获得抢断王的后卫鞠维松，这三个人构成了山东男篮在联赛初期的战力来源。大部分时间，叶鹏成为了这支队伍的主帅。

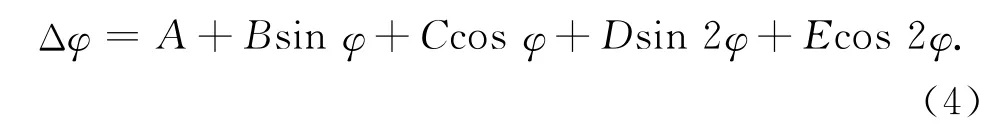
罗差的补偿系数需要通过测量电子罗盘0°～360°间离散的采样点处的补偿值，并拟合出补偿曲线Δφ＝f（φ），于是α＝φ＋f（φ）。

2 补偿值自动测量方法及误差分析

2.1 补偿值自动测量方法

将遥控测量船置于水中，使用RTK接收定位数据，将船的速度设置为最大，并使舵机方向置于偏右的固定位置，使其顺时针方向前行。测量船走过的轨迹将近似圆形。测量过程中以固定频率4Hz采集船的RTK平面坐标数据和电子罗盘的方向值，测量两圆周后停止测量。

测量船在圆周运动过程中，电子罗盘在0°～360°之间均匀采样，接收机在航迹上均匀采样，如图1所示。

图1 测量原理示意图

图1中，轨迹上的每一个点的航向α′i为当前点到下一点连线的方位角和上一点与当前点方位角的平均值，以P1为例，其航向为其航向计算为

电子罗盘在当前点的方向值为φi，由此可计算其对应的补偿值Δφi＝αi-φi，进而得到一系列的罗盘补偿值采样点（φi，Δφi）。

采用最小二乘求解电子罗盘补偿系数，即式（4）中A，B，C，D，E，进而求得电子罗盘在各方位上的补偿值。

根据式（4）总罗差方程用矩阵的形式表示为

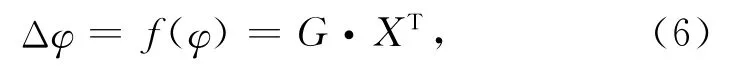
式中：Δφ为总罗差；G为方程系数。

X为总罗差补偿参数

通过如上方程，根据最小二乘原则可列出如下误差方程

其中，H为如下矩阵：

求出如上数据的最佳拟合参数

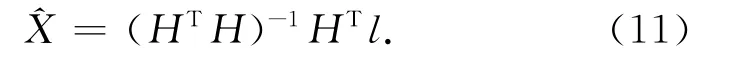
拟合中误差为

以3σ为限差，将观测总罗差与拟合总罗差之差大于3σ的测量粗差剔除，重新进行补偿参数的计算，直到没有粗差出现。

2.2 误差分析与方法改进

测量方法的误差包括两部分：一部分为罗盘的测量误差及接收机定位误差，这两种误差属于偶然误差；另一部分为风浪引起的航向测量误差，由于风浪的影响，遥控测量船的航迹并不完全是圆形，而是在圆形的基础上沿着风向前行，使得由式（5）计算得到的航向值与其真值有一定的偏差Dα，该误差为系统误差。

对于系统误差Dα，可以通过改进测量方法来消除：在船顺时针测量完成后，将船的舵机方向偏左侧，让测量船以相同的速度逆时针运行相同时间，对两次数据进行综合处理消除系统误差；对于偶然误差可以通过尽量多的采样来削弱。

改进后的补偿方程确定方法如下：

式中：f1（x）为利用顺时针测量数据，根据式（11）计算得到的电子罗盘误差补偿方程；f2（x）为利用逆时针测量数据根据式（11）计算得到的电子罗盘误差补偿方程，则该方程的拟合中误差为

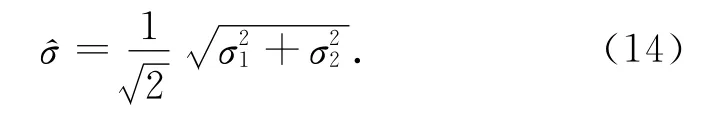
式中：σ1为由式（12）计算得到的顺时针拟合中误差；σ2为由式（12）计算得到的逆时针拟合中误差。

3 实验分析

如图2所示，两组数据分别为遥控测量船顺时针行驶两周测得的92个数据和逆时针行驶两周测量得到的100个数据。

图2 原始数据

从图2中可看出，数据有明显的规律。最大罗差之差为18.2°。如果不对其进行补偿将对便携式测量船自动导航产生影响。

采用本文的方法对以上两组数据进行计算，结果如图3所示

图3 拟合结果

顺时针测量数据拟合结果如图3中的曲线a，其补偿参数为［2.970 4 0.005 7 0.045 7 0.055 1-0.048 2］，剔除粗差后，拟合中误差为σ1＝0.030。逆时针测量数据拟合结果如图3中曲线b，其补偿参数为［3.012 1 -0.009 1 0.028 3 0.055 5-0.054 8］，剔除粗差后，拟合中误差为σ2＝0.027。根据式（13）可计算得到总罗差的补偿方程φ（x），该方程曲线为图3中的曲线c，根据式（14）计算得总罗差补偿方程的拟合中误差＾σ＝0.028，即1.64°，通过得到的补偿参数对两组数据进行总罗差补偿，补偿后的总罗差最大为3.5°，可以满足便携式遥控测量船的导航要求。