快速线调频小波原子滤波与尾传动轴振动辨识＊

陈 忠，张宪民，符和超，陈隆生

（1.华南理工大学机械与汽车工程学院，广东 广州510641；2.中国人民解放军75752部队，广东 佛山528100）

引 言

传动系统（包括齿轮箱、尾传动轴等）是直升机动力系统的重要组成部件，对其进行状态监测与振动信号分析是确保直升机的飞行安全和效能有重要意义［1］。传统的振动信号分析方法包括基于时标、周期、无转角传感的时域同步平均方法；基于傅里叶变换的功率谱、倒谱和解调分析的频域分析方法；基于小波、魏格纳（Wigner）、经验模式分解等时频域分析方法［1，2］。直升机启动及变速过程中包含了丰富的传动系统状态信息，以上方法不能很好适应变速工况的状态特征提取。

朱利民等针对变速机械弱时变响应信号的特征，采用离散频谱多点平均幅值修正法的理论和方法，改善信号处理效果［3］。李志农等提出了一种结合双谱和因子隐Markov模型的因子隐Markov模型状态识别法用于旋转机械升降速过程的故障诊断［4］。Candès等于2006年提出线调频小波路径追踪方法，利用基于多尺度线调频小波（chirplet）及chirp图的内在信息构建结构化算法，实现最优路径追踪［5］。彭富强、梅检民等进一步将稀疏信号分解与线调频小波路径追踪算法进行结合，提出一种基于多尺度线调频基的稀疏信号分解方法，并把该方法用于时变信号的特征提取上［6～8］。本文将采用chirplet匹配追踪方法实现直升机尾传动轴的振动信号稀疏分解与振动初步辨识，在此基础上提出原子滤波方法建立时变特征的稀疏分解，并完成尾传动轴某一时变特征的提取。

1 快速线调频小波匹配追踪算法及原子滤波分解

1.1 快速线调频小波匹配最追踪算法

Mallat和Zhang提出的匹配追踪算法能够实现一种基于原子字典投影方法的信号稀疏分解方法［9］。原子字典的选择和匹配追踪算法是基于匹配追踪方法实现信号稀疏分解的关键。用于匹配追踪算法的原子主要包括正弦函数、余弦函数、离散余弦函数等傅里叶基函数和小波、小波包和克罗内克脉冲函数等时频函数。而线调频小波是一种高斯线调频函数，带有尺度s、平移时间u、频率ξ、调频斜率c四个参数，具有极大的信号表达自由度，其原子表达如下式所示

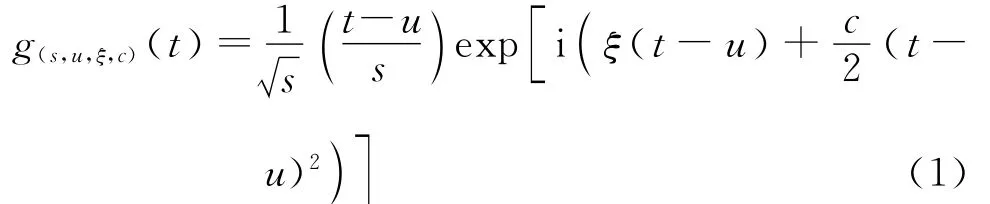
标准的匹配追踪算法是一种贪婪的信号投影分解算法，它通过遍历具有冗余特征的原子字典D＝｛gγ，（s，u，ξ，c）记为γ｝，迭代计算m阶分解残余信号Rm－1x，直到达到迭代条件要求，算法具体如下：

1）计算｜〈Rm－1x，gγ〉｜2，gγ∈D

2）选择最佳原子

3）更新投影残余信号

针对长度为N的离散信号的标准匹配追踪算法计算量大（其计算复杂度为O（MN2lgN））的缺点，由于chirp字典是Garbor字典的扩展，Gribonval［10］采用“脊”追踪思想，通过在Garbor字典寻优构建Garbor子字典Dm，并采用快速估计方法得到最佳chirp原子。通过迭代计算最终得到规模很小的chirp原子字典，然后采用正则匹配追踪算法实现信号的快速稀疏分解。该快速匹配追踪算法的计算复杂度为O（MN）。

1.2 基于原子筛选的滤波分解

通过采用快速线调频小波匹配追踪算法可快速实现复杂信号具有4自由度原子的稀疏表达。但对于复杂时变机械振动信号来说，还不足以反映机械设备振动的本质特征。为此，提出一种基于快速线调频小波匹配追踪算法的原子筛选滤波分解方法，实现振动信号的信号分解。具体算法如下：

1）对机械振动信号x（t）进行快速线调频小波匹配追踪投影，得到选择的原子字典及投影参数：尺度g′γ.s，幅值g′γ.v，中心频率g′γ.ξ和调频斜率g′γ.c。由此，得到各投影原子在时频平面上的几何框架g′.frame，该几何框架与其尺度、中心频率和调频斜率有关。

2）根据机械系统振动的先验知识，进行基于带宽与幅值约束的原子初步筛选，更新原子字典D′。筛选的 原 子g′γ.满 足 条 件：g′γ.v≤Vthresh∪ξ0≤g′γ.ξ≤ξ1。

3）过滤冲击特征原子，更新原子字典D′。所过滤的具有冲击特征原子g′γm满足条件：0≤g′γ.s≤2。

4）针对最新的原子字典D′，采用原子在时频平面上的几何框架的重叠与邻近原则进行聚类，得到所需要的特征原子类Dn，其中∪Dn＝D′，∩Dn＝0，n＝1，2，…，N。

5）去除与原子趋势不同的毛刺原子g′γn，更新原子类Dn，并得到其上的信号投影xn（t）。过滤的原子满足的条件是其中i为原子类Dn中的原子序号；ε为人为设定的常量；函数fc（ξ）为原子类Dn中各原子中心频率的三次样条拟合线在频率ξ处的斜率。

通过以上基于快速线调频小波匹配追踪的原子滤波算法可实现机械振动信号的自适应分解，同时避免了经验模式分解（EMD）、小波分解等方法对带有冲击特征信号分解的能量泄露问题。

2 直升机尾传动轴振动辨识

2.1 直升机地面振动测试系统

直升机尾传动轴用于主减速器和尾减速器之间的动力传递，并形成由通过法兰联接的多段柔性细长轴构成的多支承柔轴系统。针对某型直升机尾传动轴振动测试分析，建立振动测试系统，如图1所示。在直升机尾传动轴靠近尾桨的支承处通过螺栓安装压电加速度传感器，通过IOTechZonicbook 618动态分析仪及eZanalyst信号分析软件完成振动信号的采集。

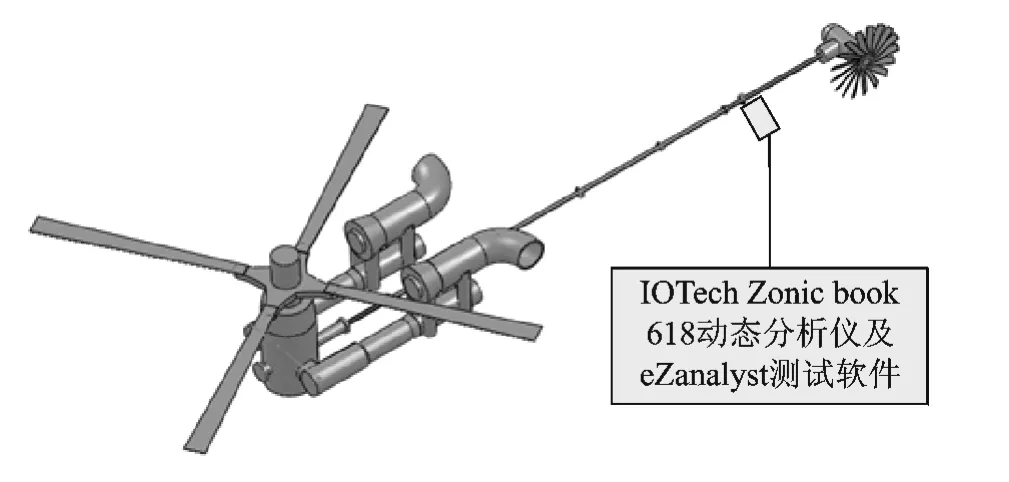
图1 直升机地面振动测试系统Fig.1 Ground vibration testing system for a helicopter

2.2 尾传动轴启动过程振动分析

直升机按照正常地面试车过程从静止到稳态工作转速。通过所搭建的振动测试系统完成直升机尾传动轴的全程振动信号采集。由于动态信号采集系统的限制，不能连续采集，因此采取分段全程信号采集的方法。按时间顺序选择有代表性的分段采集数据，见图2所示。显然，s1～s5对应直升启动到稳态运行之前阶段的振动信号，有明显的冲击现象；s6对应直升机处于稳态运行的振动信号，表现出稳态振动特性。

为了更清楚地从时频全貌上理解直升机尾传动轴振动的情况，分别对这6段共19.2s的数据进行快速线调频小波匹配追踪稀疏分解，各分解为300个原子的投影。分解的时频结果如图3，4（a），5（a），6（a），7（a），8所示，图中幅值单位为dB，用彩色表示（赤橙黄绿青蓝紫，0dB对应最大幅值用红色表示，－75dB对应最小幅值用紫色表示，黑色为背景色）。

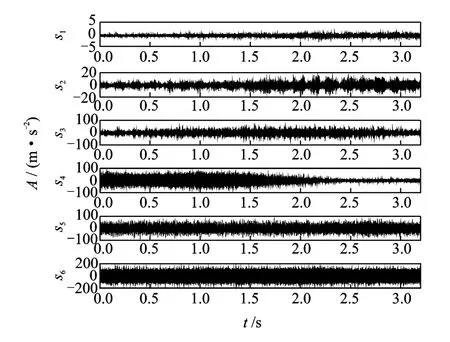
图2 直升机尾传动轴全程振动信号Fig.2 Vibration signals of a tail driving shaft of a helicopter in a whole running process

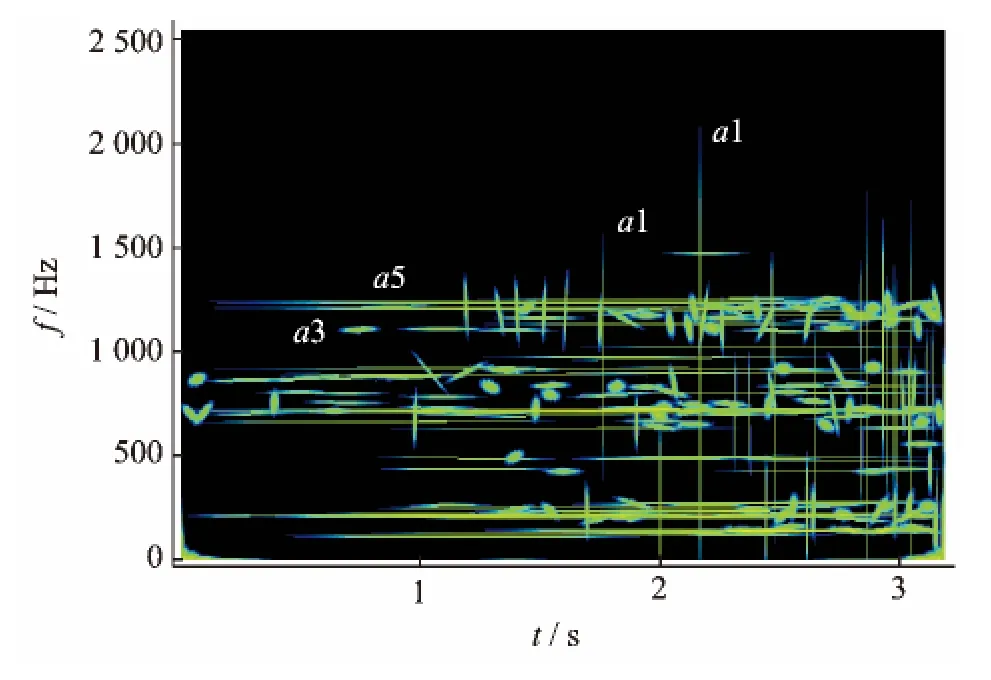
图3 信号s1的线调频小波匹配追踪时频图Fig.3 Time－frequency spectrum of signal s1using chirplet matching pursuit method

2.2.1 基本原子特征分析

由于各时频结果显示的是各高斯chirp原子的时频图的叠加，明确各高斯chirp原子的属性特性，有助于理解各段振动信号匹配追踪稀疏分解的时频图的物理意义。高斯chirp原子的主要属性包括尺度s、幅值v、调频斜率c、中心频率ξ和中心时间t。当原子尺度s较小（1≤s≤2），原子对应的是振动冲击特征，如图3，4（a），5（a），6（a），7（a），8中的a1原子所示；当原子尺度s很大，几乎是整个信号的宽度，同时调频斜率满足：0≤c≤ε，ε为一极小量，这时原子对应的是稳态简谐振动，如图8的原子a2所示；当原子尺度s较小，时频图上表现为一“斑点”，这时原子对应为噪声，如图3，4（a），7（a），8的原子a3所示；当原子调频斜率c不为0或极小，时频图上原子为一斜线，表明振动信号有线性调频现象，如图5（a），6（a），7（a）原子a4所示，或者有多段斜线构成一趋势变化，表明存在复杂的调频现象，如图7（a）原子a4表示存在具有线性调频趋势的复杂调频现象；对于旋转机械变速工况，如果原子尺度较大，同时调频频率c满足：0≤c≤ε，ε为一极小量，这时该原子表示机械系统的共振特征，其中心频率ξ对应的系统的固有频率，如图3，5（a），6（a），7（a）的原子a5所示，同时该原子的中心频率一致，表明在直升机的不同启动阶段激励起静止结构的共振。

图4 信号s2的线调频小波匹配追踪时频图Fig.4 Time－frequency spectrum of signal s2using chirplet matching pursuit method

2.2.2 各变速阶段振动辨识

旋翼、尾传动轴和尾桨叶的工作转速分别为350，4 009和3 665r／min，直升机从开车启动到停机转速变化情况：1）转速从0～40%（最高转速的40%）由电机带动，时间为0～30s；2）转速从40%～90%由电机和发动机共同带动，时间大概30s以内；3）转速从90%～100%由发动机单独带动，时间10s内；4）从最高转速到停车（指发动机输出功率为0）大概30s。由于直升机自由涡轴发动机准确启动过程、主减速器传动参数等未知，不能由这些时频图详细分析各原子或原子族对应的机械系统物理特征。但可以通过提取调频斜率为0～ε的水平原子，评估变速工况下引起的结构有阻尼固有频率。对信号s2～s5的匹配追踪结果进行原子滤波，设定调频斜率c范围为0～0.01Hz／s，尺度范围为256～16 384（以消除噪声原子，数值对应采样数），分别提取出相应的水平原子，如图4（b），5（b），6（b），7（b）所示（图中数字为各原子的中心频率，单位为Hz）。

图5 信号s3的线调频小波匹配追踪时频图Fig.5 Time－frequency spectrum of signal s3using chirplet matching pursuit method

因为直升机传动系统是一个复杂的转子系统，存在随转速变化的歌氏力及复杂的空气动力学效应，其转子系统有阻尼固有频率会随转速的变化发生偏移［11］。因此，采取对不同提速阶段的振动信号辨识直升机的有阻尼固有频率的策略。

（1）信号s2对应低速变转速下的工况，从图4（a）可以看出，振动信号集中在0～1 000Hz，因而可以从提取的水平原子分析该阶段0～1 000Hz范围的系统固有频率成分。从图4（b）可以得到，827.5～865Hz，230Hz，285Hz，667～682.5Hz对应该阶段系统的固有频率。这些原子尺度大小不一，反映了模态阻尼不同，振动衰减快慢不同。

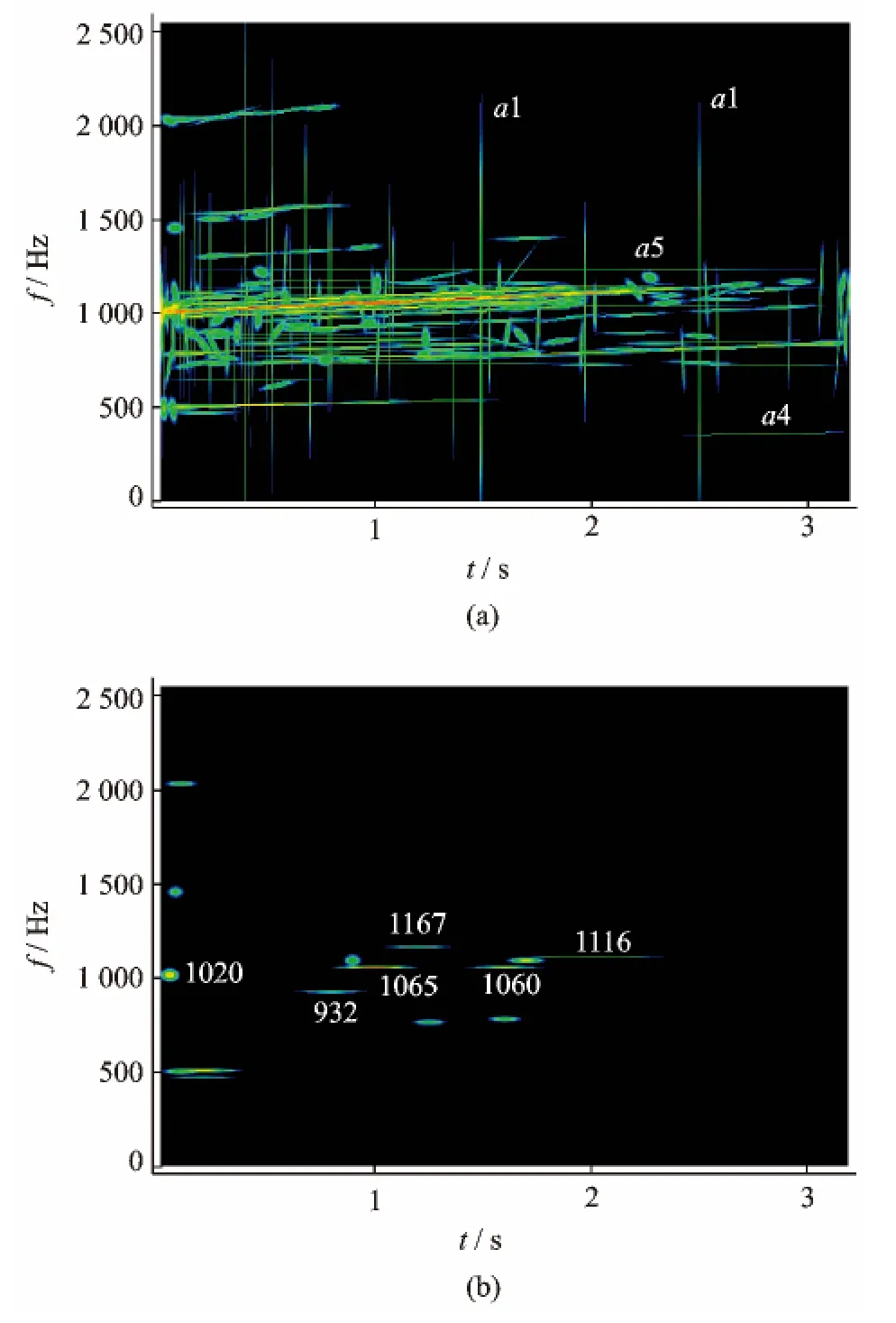
图6 信号s4的线调频小波匹配追踪时频图Fig.6 Time－frequency spectrum of signal s4using chirplet matching pursuit method

（2）信号s3对应了低中速变速阶段的工况，从图5（a）可以看出，振动信号集中在500～1 500Hz。从提取的水平原子图（图5（b））看出，存在570～626 Hz，887～995Hz，1 250～1 330Hz三处系统固有频率点。随着转速提高，高阶的固有频率振动被短时激励起来。

（3）信号s4对应了中速提速段的工况，从图6（a）可以看出，振动信号集中在500～2 000Hz，并且振动主要集中在1 000Hz附近。从提取的水平原子图（图6（b））看出，1 020～1 116Hz固有频率特征特别明显，这也印证了1 000Hz附近的振动量较大的现象。

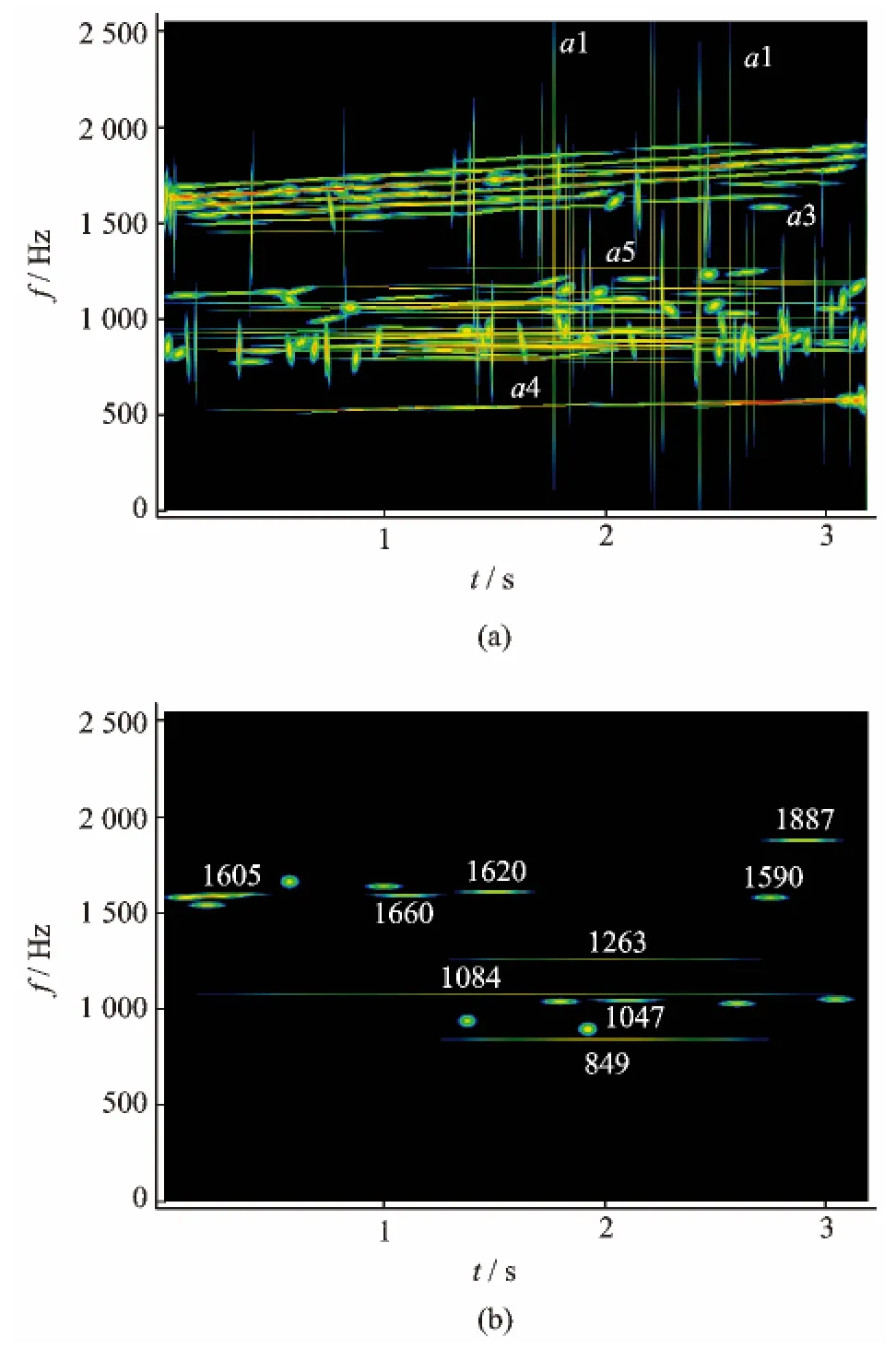
图7 信号s5的线调频小波匹配追踪时频图Fig.7 Time－frequency spectrum of signal s5using chirplet matching pursuit method

（4）信号s5对应了中高速提速段的工况，从图7（a）可以看出，振动信号集中在7 00～2 000Hz，表现出两个振动成分族（700～1 200Hz，1 400～2 000 Hz）。从提取的水平原子图（图7（b））看出，存在849，1 081，1 263，1 605～1 620和1 887Hz系统固有频率。特别是849，1 081，1 263Hz原子尺度较大，反映出该阶段在这些频率点振动激励的持续性。

2.2.3 稳态工作阶段振动辨识

根据已知信息，尾传动轴额定转频为66.8Hz，尾桨叶额定激励频率为671.9Hz（因尾桨叶数目为11）。根据图8尾传动轴稳态振动的分析结果，图中原子a2的中心频率对应尾桨叶激励频率。同时时频图中明显存在多条间隔接近66.8Hz的水平原子。为了进一步确定，对信号s6进行希尔伯特解调谱分析。如图9所示，存在65Hz峰值，这进一步说明该阶段存在尾传动轴转频调制现象。因此，由稳态分析结果，可以追踪尾传动轴尾桨叶激励频率的原子轨迹，从而可以深入分析直升机启动过程。

图8 信号s6的线调频小波匹配追踪时频图Fig.8 Time－frequency spectrum of signal s6using chirplet matching pursuit method

图9 信号s6的希尔伯特解调谱Fig.9 Demodulation spectrum of signal s6using Hilbert method

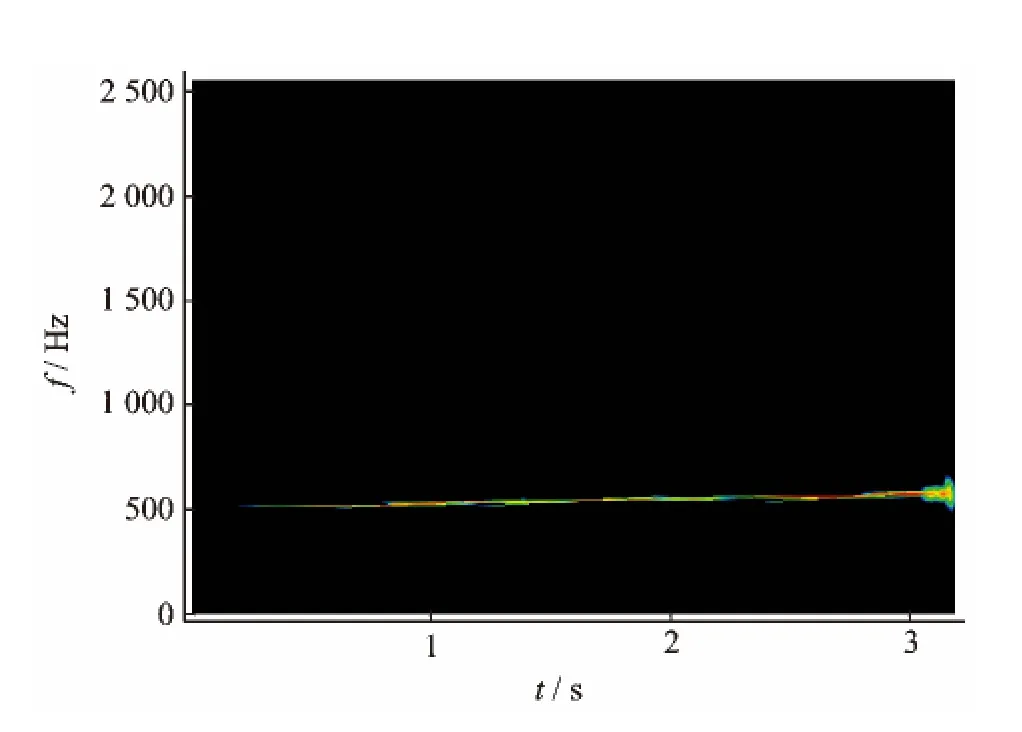
图10 信号s5的线调频小波匹配追踪原子滤波时频图Fig.10 Time－frequency spectrum of signal s5using the atomic filtering

2.3 尾传动轴振动特征的路径追踪

为追踪尾传动轴尾桨激励振动特征，采用基于快速线调频小波匹配追踪的原子滤波算法，分解对应的尾传动轴上的尾桨激励振动特征原子。根据尾传动轴全程振动信号的线调频小波匹配追踪的稀疏分解结果的分析以及尾传动轴已知参数，按照原子滤波算法的要求，确定滤波频带及原子最小幅值阈值，对振动信号s5，s6进行原子滤波筛选，分解后的信号时频投影结果见图9，10。很显然，算法能够筛选出对应的原子，并滤去了重叠的冲击特征（如图7所示）和毛刺原子（如图8所示）。

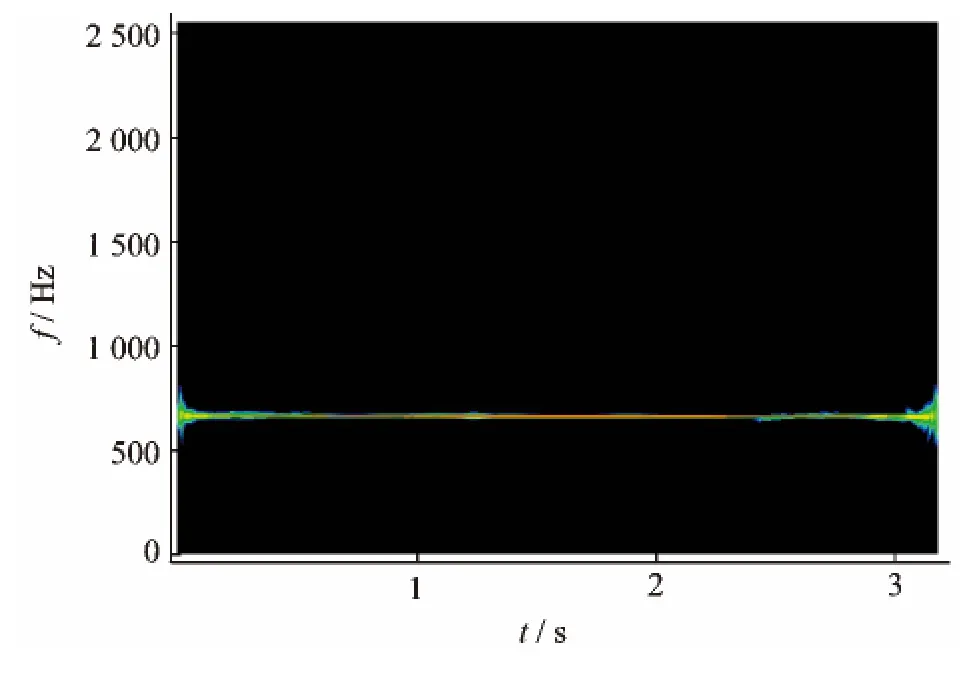
图11 信号s6的线调频小波匹配追踪原子滤波时频图Fig.11 Time－frequency spectrum of signal s6using the atomic filtering

根据图10及相应的原子构成，可知该段线性特征并不是由一个原子构成，而是由多个尺度不同的原子构成，且其调频斜率各不相同，分别是0.73，0.8，50，1.87，1.08，58，15.7，16.5，22，11，81Hz／s等。由图10可知，其平均线性调频斜率为24.5 Hz／s，对应尾传动轴转速变化为133.6r／min／s。这些现象说明，在机师进行线性加速的过程中，实际的转速存在较大的波动，这些波动必然会产生冲击，引起结构共振。

3 结 论

（1）提出了一种基于快速线调频小波匹配追踪的原子滤波算法，该算法能够有效滤除冲击特征与毛刺原子，克服信号分解中的混叠。运用该算法准确提取了直升机尾传动轴的尾桨激励振动特征。

（2）快速线调频小波匹配追踪算法具有快速、准确的特点，在直升机传动系统（包括尾传动轴）的振动监测方面较其他传统方法有一定优势。本文运用该方法成功辨识了直升机尾传动轴的振动特征。

［1］ 沈国际.振动信号处理技术在直升机齿轮箱故障诊断中的应用［D］.长沙：国防科学技术大学，2005.SHEN Guoji.Research on vibration signal processing techniques and applications to fault diagnosis of helicopter gearbox［D］.Changsha：National University of Defense Technology，2005.

［2］ Blunt D M，Keller J A.Detection of a fatigue crack in a UH－60Aplanet gear carrier using vibration analysis［J］.Mechanical Systems and Signal Processing，2006，（20）：2 095—2 111.

［3］ 朱利民，钟秉林，熊有伦.变速机械弱时变信号幅值谱校正的多点平均法［J］.振动工程学报，2001，14（1）：47—52.Zhu Limin，Zhong Binglin，Xiong Youlun.Amplitude correction approach using average of several points in discrete spectrum for analyzing the dynamic signal of rotating machinery with varying speed［J］.Journal of Vibration Engineering，2001，14（1）：47—52.

［4］ 李志农，丁启全，吴昭同，等.旋转机械升降速过程的双谱－FHMM 识别方法［J］.振动工程学报，2003，16（2）：171—174.Li Zhinong，Ding Qiquan，Wu Zhaotong，et al.Study on bispectrum－FHMM recognition method in speed－up and speed－down process of rotating machinery［J］.Journal of Vibration Engineering，2003，16（2）：171—174.

［5］ Candès E J，Charlton P R，Helgason H.Detecting highly oscillatory signals by chirplet path pursuit［J］.Applied and Computational Harmonic Analysis，2008，24（1）：14—40.

［6］ 彭富强，于德介，刘坚.一种基于多尺度线调频基的稀疏信号分解方法［J］.振动工程学报，2010，23（3）：333—338.Peng Fu－qiang，Yu De－jie，Liu Jian.Sparse signal decomposition method based on multi－scale chirplet［J］.Journal of Vibration Engineering，2010，23（3）：333—338.

［7］ 彭富强，于德介.基于多尺度线调频基稀疏信号分解的轴承故障诊断［J］.机械工程学报，2010，46（7）：88—94.Peng Fu－qiang，Yu De－jie.Sparse signal decomposition method based on multi－scale chirplet and its application to bearing fault diagnosis［J］.Journal of Mechanical Engineering，2010，46（7）：88—94.

［8］ 梅检民，肖云魁，周斌，等.基于FRFT的改进多尺度线调频基稀疏信号分解方法［J］.振动工程学报，2013，26（1）：135—142.MEI Jian－min，XIAOYun－kui，ZHOU Bin，et al.Improved multi－scale chirplet sparse signal decomposition method based on Fractional Fourier Transform［J］.Journal of Vibration Engineering，2013，26（1）：135—142.

［9］ Mallat S，Zhang Z.Matching pursuit with time－fre－quency dictionaries［J］.Signal Processing，1993，41（12）：3 397—3 415.

［10］Gribonval R.Fast matching pursuit with a multiscale dictionary of Gaussian chirps［J］.IEEE Transaction on Signal Processing，2001，49（5）：994—1 001.

［11］Ewins DJ.Modal Testing：Theory，Practice and Application，Second Edition［M］.Baldock，Hertfordshire，England：Research Studies Press Ltd.，2000：80—98.