考虑弹塑性变形机制的结合面法向接触刚度建模＊

张学良，陈永会，温淑花，兰国生，丁红钦，王南山，张宗阳

（1.太原科技大学机械工程学院，山西 太原030024；2.东南大学机械工程学院，江苏 南京211100；

3.西安交通大学机械工程学院，陕西 西安710049；4.徐州徐工基础工程机械有限公司，江苏 徐州221004）

引 言

机械结构都是组合结构，其中包含了各种各样的结合面，结合面的存在使得机械结构不再具有连续性，导致了其结构静动态特性的复杂性。结合面的接触刚度常常是机械结构整体刚度的重要组成部分，如对机床结构而言，其结合面的接触刚度约占机床总刚度的60%～80%［1］。关于结合面接触刚度的研究［3～6，9～10，12～14］，往 往 仅 考 虑 了 结 合 面 微 凸 体弹性接触变形和塑性接触变形两个阶段，而忽略了微凸体的弹塑性接触变形。文献［2，18］分别首先提出了粗糙表面接触的三维和二维接触分形模型；文献［3，4］最早建立了结合面法向接触刚度分形模型，在此基础上，文献［4］研究建立了考虑微接触域扩展因子影响的结合面法向接触刚度分形模型，之后，文献［7，9，10，12～14］再次对结合面法向接触刚度模型进行了改进，但都没有考虑弹塑性接触变形，而仅仅考虑了弹性接触变形和塑性接触变形。文献［15］提出了包含弹性变形、弹塑性变形和塑性变形情况下的接触模型，但该模型对于弹塑性变形区间的预估不够精确，与文献［16］有限元分析结果存在较大误差。文献［7，8，11］基于文献［16］关于弹塑性变形阶段的分析结果，在考虑结合面微凸体弹性变形、弹塑性变形和塑性变形的基础上，分别建立了结合面法向接触刚度和静摩擦因数的统计模型，并通过仿真分析揭示了结合面微观形貌对结合面法向接触刚度和静摩擦因数的影响规律。但是，法向接触刚度统计模型中的粗糙表面统计参数与取样长度和测试仪器的分辨率有关，不具有客观唯一确定性。鉴于此，本文基于接触分形理论和MB模型及文献［16］的弹塑性接触变形机制，综合考虑结合面微凸体的弹性接触变形、塑性接触变形和弹塑性接触变形的两个不同阶段，建立了结合面法向接触刚度的分形模型，并通过仿真揭示了弹塑性接触变形机制及相关参数对结合面法向接触刚度的影响，进而应用实验实例验证了该模型的正确可信性。该模型的特点是具有尺度独立性，综合考虑了结合面微凸体的弹性接触变形、塑性接触变形和弹塑性接触变形的两个不同阶段，因此更加符合结合面实际接触情况，具有较高的计算精度。

1 结合面微凸体接触变形机制

结合面是由两个粗糙表面接触形成，通常将两粗糙表面的接触简化为一粗糙表面和一刚性平面的接触，对于粗糙表面的单个微凸体，将其等效为半球体，其等效曲率半径为R，如图1（a）所示。当在法向载荷p作用下，接触区域半径为r，法向接触变形为δ，如图1（b）所示。

图1 等效微凸球体和刚性平面接触前后状态Fig.1 The two states of the equivalent microcontact sphere against a rigid flat plane before and after contact

1.1 微凸体弹性接触变形阶段

当微凸体的接触变形在完全弹性变形范围时，根据Hertz理论，球体接触变形量为δ时，单个微凸体的圆形接触面积ae和法向接触载荷Fe分别为

式中E为复合弹性模量，，E2为两接触材料的弹性模量；ν1，ν2为两接触材料的泊松比。

1.2 微凸体弹塑性变形阶段

文献［16］利用有限元法对微凸体弹塑性变形阶段进行了分析，当微凸体变形量大于弹性临界变形量δc时，开始发生屈服现象，微凸体即进入弹塑性变形区域，弹性临界变形量δc可表示为［17］

式中H为较软材料的硬度，对于大部分延性材料，硬度和屈服强度Y之间关系为H＝2.8Y；根据文献［17］，硬度系数K和较软材料的泊松比ν之间的关系为K＝0.454＋0.41ν。

根据文献［16］的研究结果，弹塑性变形区域的范围介于δc≤δ≤110δc，并将弹塑性区域进一步划分为两个区域，变形量在δc≤δ≤6δc范围内，屈服区域都发生在接触面下方，而当变形量随载荷逐渐增加时，接触面下方的屈服区域逐渐扩大。当变形量为δ＝6δc时，屈服区域由接触面下方扩大至接触表面。当变形量为δ＝68δc时，屈服区域扩大至整个接触表面。但当平均接触压力仍小于材料的硬度，当变形量增加至δ＝110δc时，平均接触压力才等于硬度。所以当变形量达到弹性临界变形量δc的110倍，即δp＝110δc时，微凸体才进入完全塑性变形区域。有限元分析结果，得到微凸体弹塑性变形阶段的接触载荷、接触面积和变形量之间的关系为［16］：

当δc≤δ≤6δc时，

当6δc≤δ≤110δc时，

1.3 微凸体塑性变形阶段

当微凸体的变形量δ＞δp＝110δc时，进入完全塑性变形阶段，微凸体的接触面积和法向接触载荷可以分别表示为：

2 结合面微凸体弹塑性接触变形模型

2.1 结合面接触分形基本理论

结合面微接触点的面积分布密度函数为［18］

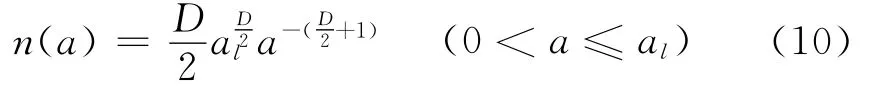
式中al为最大微接触点的面积，D为粗糙表面的分形维数。

根据文献［2，12］，结合面微凸体的变形量为

式中G为粗糙表面的分形粗糙度参数，α为大于1的常数，对于服从正态分布的随机表面，α＝1.5较符合高频密度和相位随机的情况。

根据微凸体变形量与曲率半径之关系，微凸体曲率半径为［2，12］

当δ＝δc时，相应的接触面积即为临界接触面积ac，且

2.2 结合面微凸体接触载荷与接触刚度模型

将式（11）和（12）代入式（2）中，得微凸体在弹性接触变形阶段的接触载荷为

因此，单个微凸体在弹性接触变形阶段的法向接触刚度为

将式（3），（11）和（12）代入式（5）中，得微凸体在弹塑性接触变形第一阶段的接触载荷为

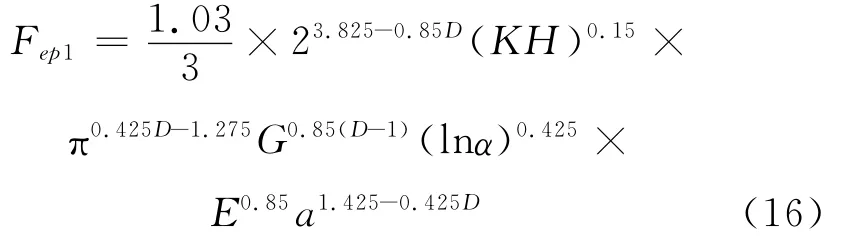
因此，单个微凸体在弹塑性接触变形第一阶段的法向接触刚度为

将式（3），（11）和（12）代入式（7）中，得微凸体在弹塑性接触变形第二阶段的接触载荷为

因此，单个微凸体在弹塑性接触变形第二阶段的法向接触刚度为

3 考虑弹塑性接触变形机制的结合面法向接触刚度分形模型

结合面的真实接触面积包括处于完全弹性接触真实接触面积、处于完全塑形接触真实接触面积和处于弹塑性接触变形第一阶段的真实接触面积及处于弹塑性接触变形第二阶段的真实接触面积，即

将式（10）代入（20），则

当结合面上的微凸体的法向接触变形量δ≥110δc时，将处于完全塑性变形范围，即当接触变形处于弹性和弹塑性阶段的微凸体才存在法向接触刚度。

因此，结合面的法向接触刚度为

将式（10），（15），（17）和（19）代入式（22）中，得

结合面法向总载荷与结合面真实接触面积之间的关系为

当1＜D＜2，且D≠1.5时

当D＝1.5时

将式（23），（25）和（26）无量纲化，得

当D≠1.5时

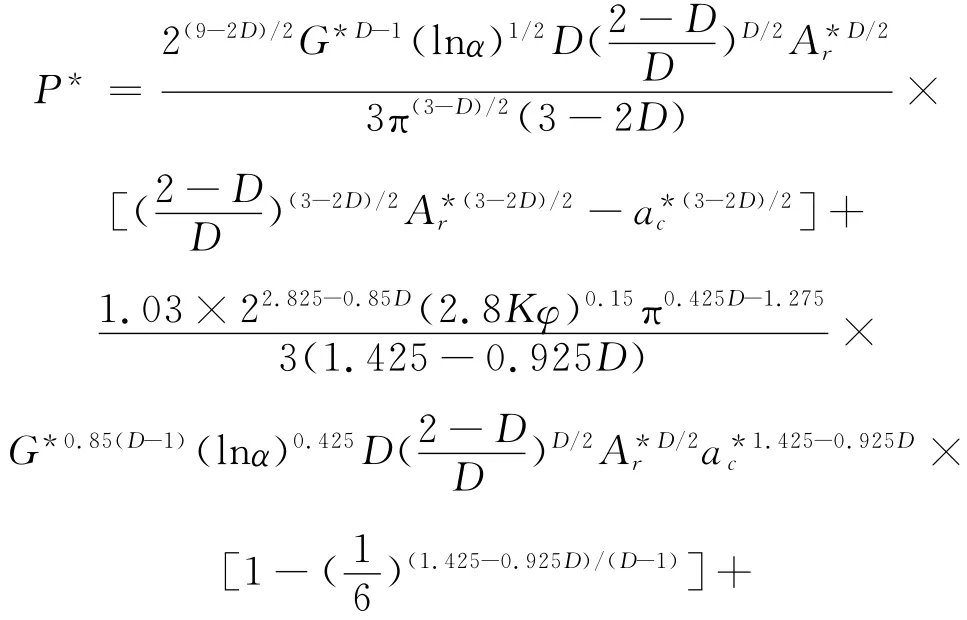
当D＝1.5时

以上即为综合考虑弹塑性接触变形机制（即弹性接触变形、弹塑性接触变形第一阶段和第二阶段、塑性接触变形）的结合面法向接触载荷和法向接触刚度分形模型，且法向接触刚度与法向接触载荷之间存在复杂的非线性关系。

需要指出的是，本文是将结合面（两粗糙表面接触）等效为一粗糙表面与一刚性平面的接触，因此上述相关式中涉及到的参数D和G实质上是等效粗糙表面的参数，其确定方法参见文献［5，13］。

4 结合面法向接触刚度分形模型的仿真及结果分析

4.1 仿真及结果

给定一固定的无量纲真实接触面积A＊r，便可以计算得到无量纲法向总载荷P＊和无量纲法向接触刚度K＊n。一般工程表面的塑性指标范围在0.7～2.5之间，所以给定φ分别为2.5，1.5和0.7，G＊分别为10－9，10－10和10－11，D分别取1.1～1.9，仿真计算结果如图2～5所示，其中图2中的“elastic and plastic”是指文献［3］中仅考虑弹性和塑性变形机制的结合面法向接触刚度分形模型的仿真计算结果，“elastoplastic”是指本文提出的考虑弹塑性接触变形机制的结合面法向接触刚度分形模型的仿真计算结果，其余图中的仿真结果数据均由本文提出的模型仿真计算获得。

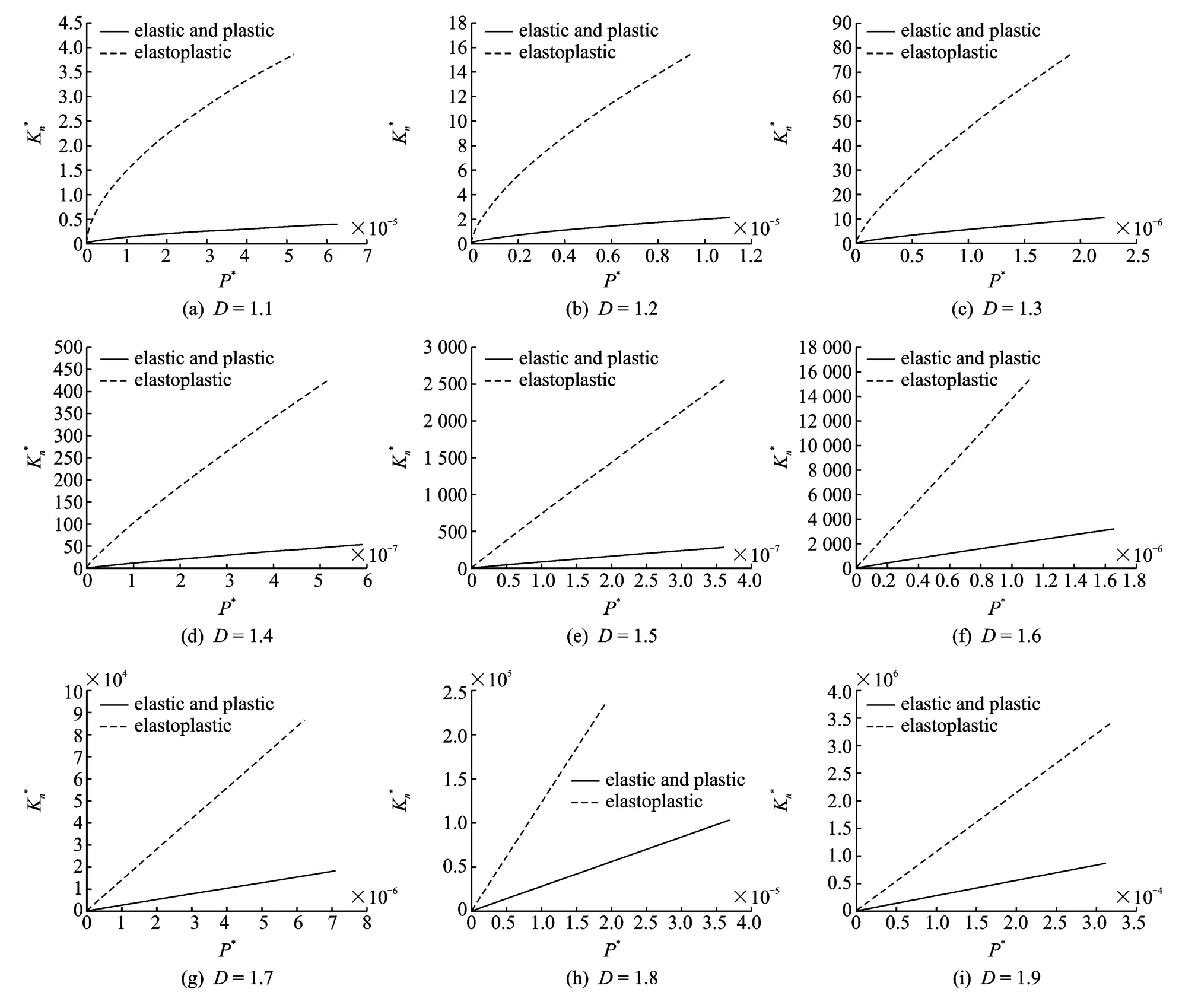
图2 K＊n随P＊的变化规律（G＊＝1.0×10－10，φ＝1.5）Fig.2 Change curves of K＊nwith P＊（G＊＝1.0×10－10，φ＝1.5）

图3 D对K＊n的影响曲线（G＊＝1.0×10－10，φ＝1.5）Fig.3 Influence curves of Don K＊n（G＊＝1.0×10－10，φ＝1.5）

图4 G＊对Kn＊ 的影响曲线（φ＝1.5）Fig.4 Influence curves of G＊on Kn＊ （φ＝1.5）

图5 φ对Kn＊ 的影响曲线（G＊＝1.0×10－10）Fig.5 Influence curves ofφon Kn＊（G＊ ＝1.0×10－10）

4.2 仿真结果分析

（1）从图2（a）～（i）可以看出，综合考虑弹塑性接触变形机制的结合面无量纲法向接触刚度K＊n大于仅考虑弹性和塑性变形机制的结合面无量纲法向接触刚度值。可见，弹塑性接触变形机制对结合面无量纲法向接触刚度影响很明显。当分形维数D＝1.1～1.4时，结合面无量纲法向接触刚度随着无量纲法向总载荷的增大而增大，且表现出较强的非线性关系；而当分形维数D＝1.4～1.9时，二者之间的非线性关系逐渐弱化并接近直线关系。

（2）从图3（a），（b）及（b），（c）可以分别看出，当分形维数D＝1.1～1.6时，结合面无量纲法向接触刚度随着分形维数D的增大而增大；而当分形维数D＝1.6～1.9时，结合面无量纲法向接触刚度随着分形维数D的增大而减小。

（3）基于上述分析结果，这里分别选取了两个代表性的分形维数值，即D＝1.3，1.7，从相应的仿真结果图4（a），（b）和5（a），（b）可以分别看出，结合面无量纲法向接触刚度随着分形粗糙度G＊的增大而减小，却随着塑性指数φ的增大而增大。

5 结合面法向接触刚度分形模型的实验实例验证

这里借助文献［13］的结合面实验装置——哑铃模型及其实验数据，对本文所建立的结合面法向接触刚度分形模型进行间接验证。

哑铃模型结合面的配对表面分别为HT250表面和45号钢表面，其中 HT250表面参数为［13］：弹性模量E1＝116GPa，泊松比υ1＝0.27，密度ρ1＝7 340kg／m3，屈服强度σy1＝240MPa，硬度H1＝700MPa；45号钢表面参数为［13］：弹性模量E2＝205GPa，泊松比υ2＝0.3，密度ρ2＝7 833kg／m3，屈服强度σy2＝353MPa，硬度H2＝500MPa。结合部的2个重要分形表征参数为［13］：D＝1.4241，G＝2.9820×10－10m。

每个螺栓的拧紧力矩分别控制为［13］：30，60，90N·m。

根据上述参数，应用本文提出的结合面法向接触刚度分形模型，可以分别计算得到三种预紧面压下的结合面法向接触刚度，与之相应的结合面切向接触刚度由文献［5］中的模型3计算得到。

将计算得到的法向和切向接触刚度以弹簧单元的等效模式嵌入到哑铃模型整体的有限元模型中。哑铃模型整体的有限元模型总共有5 100个单元、6 360个节点，其中弹簧单元108个，如图6所示。

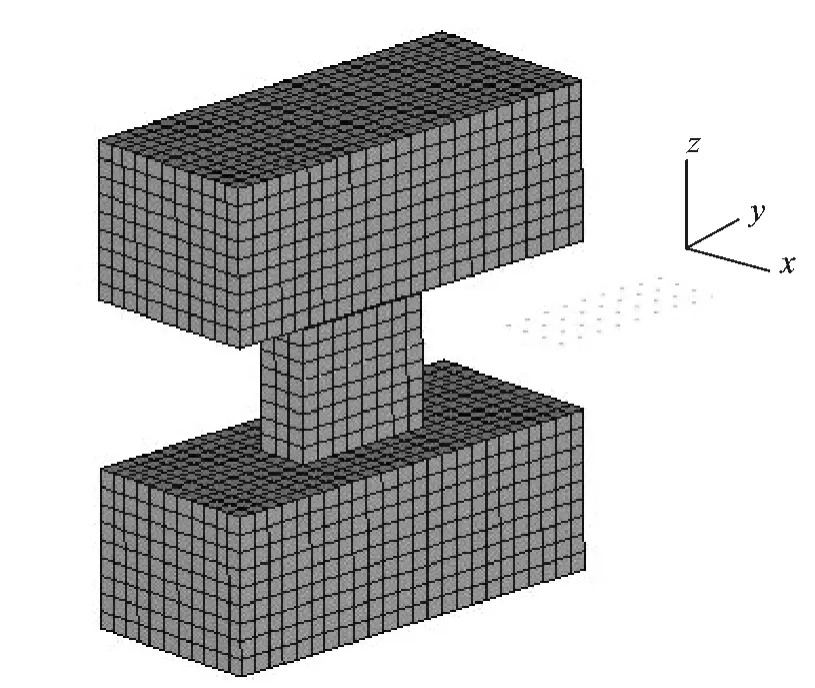
图6 哑铃模型有限元模型及结合面单元Fig.6 Finite element modeling and joint element of dumbbell

结合面的两接触面上各自对应均布36个节点，各对应节点之间嵌入3个COMBIN14单元（x，y，z三个方向，其刚度值即为上述所求得的相应的结合面接触刚度的 1／36）。根据文 献 ［13］，实验装置——哑铃模型为自由状态，因此将有限元模型的边界条件设置为自由状态。对有限元模型进行自由模态分析，得到前6阶模态振型及相应的固有频率，按照振型相似，模态固有频率定量比较的原则，表1给出了计算固有频率与文献［13］实验固有频率的比较。文献［13］和本文的计算结果均表明，哑铃模型的前6阶振型分别为绕z轴旋转（1阶）、绕y轴旋转（2阶）、绕x轴旋转（3阶）、沿x轴平动（4阶）、沿y轴平动（5阶）、沿z轴平动（6阶）。显然，绕y轴旋转（2阶）、绕x轴旋转（3阶）和沿z轴平动（6阶）的三个模态与结合面法向接触刚度关系密切，而本文关于这三个模态频率的计算结果的相对误差的绝对值除了第3阶稍大于文献［13］的结果外，其他两阶均明显小于文献［13］的结果，且本文相对误差均为负值，而文献［13］关于这三阶计算结果的相对误差有正有负，是不太合理的。其他三阶模态与结合面切向接触刚度关系密切，本文结果与文献［13］的比较这里不再多述。

可见，基于本文所提出的模型计算结合面的法向接触刚度进而用于进行哑铃模型的模态计算具有较高的计算精度，说明该模型是正确可信的，同时也具有较高的精度。

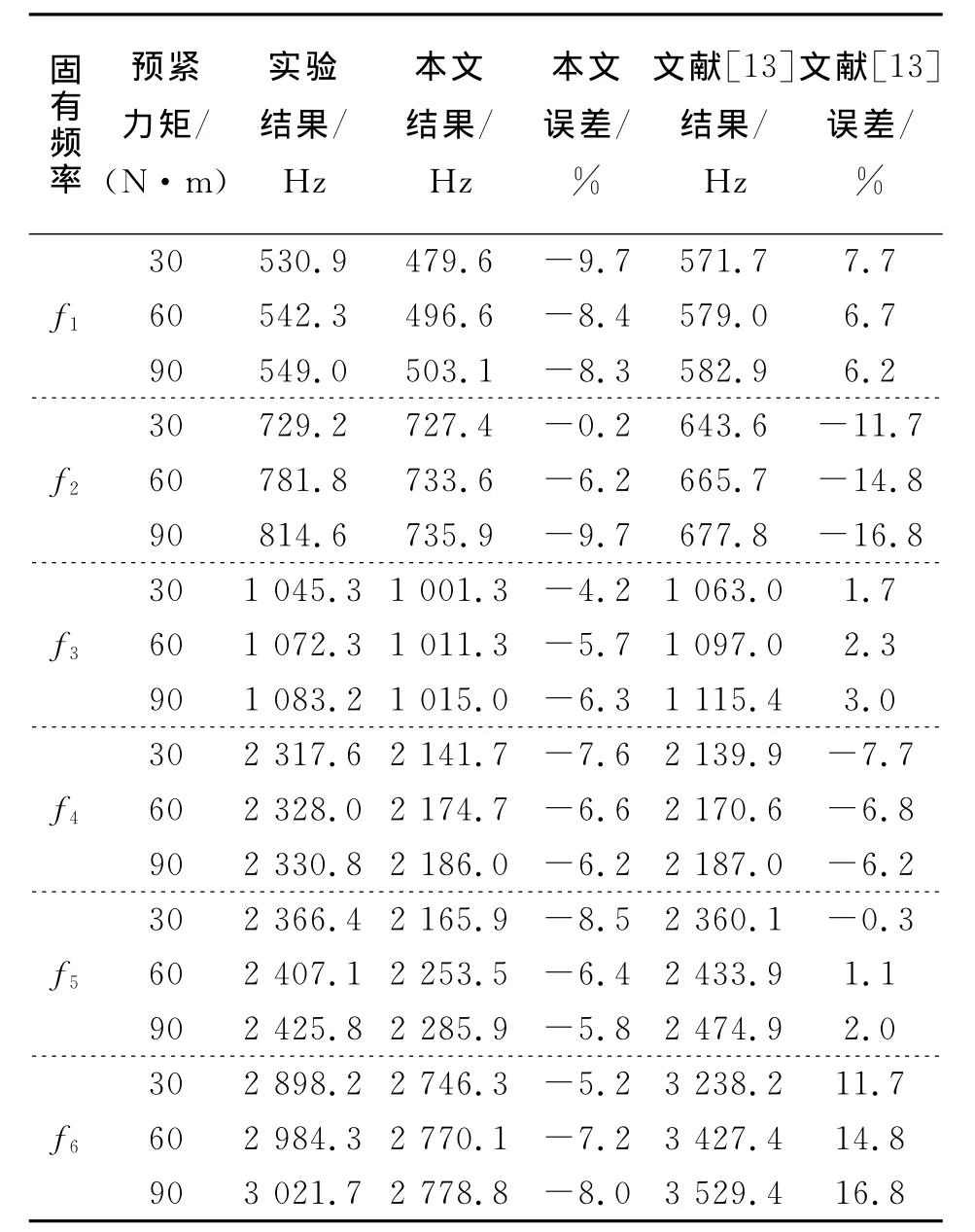
表1 计算固有频率与实验固有频率的比较Tab.1 Comparison of the computed and experimental natural frequencies

6 结 论

（1）基于接触分形理论及MB模型，综合考虑结合面微凸体接触变形所处的弹性接触变形、塑性接触变形和弹塑性接触变形的两个不同阶段，建立了结合面法向接触刚度分形模型。

（2）弹塑性接触变形机制对法向接触刚度影响明显，且考虑弹塑性接触变形机制的结合面法向接触刚度大于仅考虑弹性和塑性接触变形机制所对应的法向接触刚度。

（3）结合面无量纲法向接触刚度随着无量纲法向接触载荷的增大而增大，且分形维数取值不同而呈较强的非线性关系（D＝1.1～1.4）或近似线性关系（D＝1.4～1.9）；结合面无量纲法向接触刚度随着分形维数增大而增大（分形维数D＝1.1～1.6）或者减小（分形维数D＝1.6～1.9）；结合面无量纲法向接触刚度随着无量纲分形粗糙度的增大而减小，而随着塑性指数的增大而增大。

（4）实验实例验证说明了考虑弹塑性变形机制的结合面法向接触刚度模型是正确可信的，具有较高的计算精度。

［1］ 张学良.机械结合面动态特性及应用［M］.北京：中国科技出版社，2002.Zhang Xueliang.Dynamic Characteristics of Machine Joint Surfaces and Its Applications［M］.Press of Science and Technology of China，Beijing，2002.

［2］ Yan W，Komvopoulos K.Contact analysis of elasticplastic fractal surfaces［J］.J.Appl.Phys.，1998，（84）：3 617—3 624.

［3］ 张学良，黄玉美，傅卫平，等.粗糙表面法向接触刚度的分形模型［J］.应用力学学报，2000，17（2）：31—35.Zhang Xueliang，Huang Yumei，Fu Weiping，et al.Fractal model of normal contact stiffness between rough surfaces［J］.Chinese Journal of Applied Mechanics，2000，17（2）：31—35.

［4］ 张学良，黄玉美，韩颖.基于接触分形理论的机械结合面法向接触刚度模型［J］.中国机械工程，2000，11（7）：727—729.Zhang Xueliang，Huang Yumei，Han Ying.Fractal model of the normal con tact stiffness of machine joint surfaces based on the fractal contact theory［J］.Chinese Mechanical Engineering，2000，11（7）：727—729.

［5］ 温淑花，张宗阳，张学良，等.固定结合面刚度分形模型［J］.农业机械学报，2013，44（2）：255—260.Wen Shuhua，Zhang Zongyang，Zhang Xueliang，et al.Stiffness fractal model for fixed joint interfaces［J］.Transactions of the Chinese Society for Agricultural Machinery.2013，44（2）：255—260.

［6］ 温淑花，张学良，武美先，等.结合面法向接触刚度分形模型建立与仿真［J］.农业机械学报，2009，40（11）：197—202.Wen Shuhua，Zhang Xueliang，Wu Meixian，et al.Fractal model and simulation of normal contact stiffness of joint interfaces and its simulation［J］.Transactions of the Chinese Society for Agricultural Machinery，2009，40（11）：197—202.

［7］ 尤晋闽，陈天宁.结合面静态接触参数的统计模型研究［J］.振动与冲击，2010，29（11）：47—50.You Jinmin，Chen Tianning.Statistical model for static contact parameters of joint surfaces［J］.Journal of Vibration and Shock.2010，29（11）：47—50.

［8］ 尤晋闽，陈天宁.结合面静摩擦系数的统计模型［J］.振动与冲击，2010，29（12）：26—29.You Jinmin，Chen Tianning.Statistical model of static friction coefficient between joint surfaces［J］.Journal of Vibration and Shock，2010，29（12）：26—29.

［9］ 尤晋闽，陈天宁.基于分形接触理论的结合面法向接触参数预估［J］.上海交通大学学报，2011，45（9）：1 275—1 280.You Jinmin，Chen Tianning.Estimation for normal parameters of joint surfaces based on fractal theory［J］.Journal of Shanghai Jiao Tong University，2011，45（9）：1 275—1 280.

［10］尤晋闽，陈天宁.结合面法向动态参数的分形模型［J］.西安交通大学学报，2009，43（9）：91—94.You Jinmin，Chen Tianning.Fractal model for normal dynamic parameters of joint surfaces［J］.Journal of Shanghai Jiao Tong University，2009，43（9）：91—94.

［11］You J M，Chen T N.Statistical model for normal and tangential contact parameters of rough surface［J］.Proc.I Mech E，225（Part C）：171—185.

［12］Shuyun Jiang，Yunjian Zheng.A contact stiffness model of machined joint surfaces［J］.Journal of Tribology，Transactions of ASME，2010，（132）：1—7.

［13］田红亮，赵春华，朱大林，等.金属材料结合部法切向刚度修正与实验验证［J］.农业机械学报，2012，43（6）：207—214.Tian Hongliang，Zhao Chunhua，Zhu Dalin，et al.Modification of normal and tangential stiffness for joint interface with metallic material and experimental validation［J］.Transactions of the Chinese Society for Agricultural Machinery，2012，43（6）：207—214.

［14］Tian H L，Li B，Liu H Q，et al.A new method of virtual material hypothesis－based dynamic modeling on fixed joint interface in machine tools［J］.International Journal of Machine Tools ＆Manufacture，2011，51（3）：239—249.

［15］Zhao Y W，Maietta D M，Chang L.An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow［J］.ASME Journal of Tribology，2000，122（1）：86—93.

［16］Kogut L，Etsion I.Elastic－plastic contact analysis of a sphere and a rigid flat［J］.ASME Journal of Applied Mechanics，2002，69（5）：657—662.

［17］Chang W R，Etsion I，Bogy D B.An elastic－plastic model for the contact of rough surfaces［J］.ASME J.Tribol，1988，101（1）：15—20.

［18］Mjumdar A，Bhushan B.Fractal model of elastic－plastic contact between rough surfaces［J］.J.Tribol.，1991，（113）：1—11.