不确定性参数识别的区间响应面模型修正方法＊

方圣恩，张秋虎，林友勤，张笑华

（1.福州大学土木工程学院，福建 福州350108；2.合肥工业大学土木与水利工程学院，安徽 合肥230009）

引 言

过去20年来，有限元模型修正技术已经广泛应用于参数识别和损伤识别等领域［1，2］。当前绝大多数的模型修正方法都属于确定性方法，无法考虑结构参数和响应的不确定性，使得实用性大大降低。由于模型误差、构件几何尺寸和材料变异性、制造误差、噪声等因素的影响，不确定性广泛存在于实际结构的参数和响应中［3］，是无法回避的问题。因此，为了提高参数识别、损伤识别结果的可靠性，在有限元模型修正过程中结合概率方法进行分析是十分必要的［4］。

工程分析中可以将不确定性分为偶然型不确定性（aleatory uncertainty）和认知型不确定性（epistemic uncertainty）［5］。前者一般指结构或构件由于制造误差或材料离散性所导致的几何参数和材料变异性，可以被量化，但无法避免或人为消除；后者源于对结构的认识或测量信息上的不足（比如仅有少量的测量数据），但可以通过补充相关信息来降低甚至消除。在模型修正方面，通过结合概率分析方法可以有效考虑上述不确定性，使得修正结果的可靠性得到大大提高［6］。早期的概率模型修正方法主要针对测量误差所引起的不确定性，通过最小化测量噪声的方差来寻求参数均值的最佳估计值［6］。此外，贝叶斯方法的应用可以获得更加可靠的识别结果［7，8］，虽然修正过程会变得更为复杂、计算量更大。近些年来，采用摄动方法在参数设计点上基于截断泰勒展开的方式来表示修正方程的各个项，并以此构建概率模型修正（probabilistic model updating）过程，可以有效提高修正效率［9］，因此得到了一定的应用。但概率修正方法的精度依赖于对结构参数和响应概率分布特性的准确估计，要求有大量的测试信息来建立准确的概率分布函数。对大多数工程问题而言，考虑到测试成本和可行性，上述要求往往无法得到满足。此外，某些情况下参数或响应的上下界（极限值）对工程分析或设计来说更有实际意义，而非关注于具体的概率分布形式。此时可以采用区间数来表示结构的参数和响应，即构建区间模型修正（interval model updating）问题［10］。

目前为止，针对区间模型修正问题的相关研究还非常少。同时由于区间数运算法则和传统数学算法非常不同［11］，因此主要还是在确定性框架内进行区间反向优化（interval inverse optimization）问题的求解，并不是真正意义上的区间优化反演过程。对简单结构而言，可以通过求解区间线性方程组来估计区间参数［12］。更常见的办法是将区间模型修正问题分解为两个确定性修正过程，即分别独立修正参数的上界和下界（或者区间中值和区间半径），以避免区间数运算可能导致的优化困难［13］。此时可以采用一阶泰勒展开式来表示结构的特征矩阵，并将区间模态参数作为目标响应。当修正得到的响应区间和实测区间基本吻合时，即可认为优化过程收敛，其间可以采用传统的优化算法进行求解［14］。值得注意的是，区间算法的运算过程普遍存在着一个问题，即区间扩张（intervals overestimation）现象。该问题是由于区间变量在区间方程中多次出现所导致的，可以采用顶点法（vertex solution），通过合理组合参数的上下界求解响应区间［15］。顶点法对求解简单结构的特征值问题（频率）非常有效［16］，但其要求结构的刚度和质量矩阵是参数的线性函数。该条件对于复杂结构而言通常无法满足，因此是顶点法的重要应用缺陷。与此同时，该方法也不能采用特征向量（模态振型）作为响应，因为此时无法保证参数－响应关系的单调性［17］。因此，有必要寻求一种更为通用的方法求解区间模型修正问题。此外，区间模型修正过程的计算效率也值得关注。为了提高修正效率，可以采用元模型（meta－model，如响应面模型和Kriging模型）替代有限元模型，以建立结构参数和响应之间的关系式。然后通过不断调整参数区间的大小，并在每个迭代步开始时重构Kriging模型实现修正过程［17］。这种方法具有比顶点法更优的通用性，但其修正过程比较复杂且计算量大，不利于在复杂结构问题上的应用。

本文将传统响应面模型和区间算法相结合，提出了区间响应面模型（interval response surface model，缩写IRSM）的概念，使得区间模型修正过程中可以直接在IRSM表达式上进行区间数运算和优化计算，避免了将问题分解为数个确定性过程来分别求解，从而大幅提高了修正效率。此外，本文方法对结构参数－响应之间的关系（单调或非单调，线性或非线性）没有要求，且可以同时采用特征值和特征向量作为目标响应。更重要的是，采用区间响应面模型不会发生区间扩张现象，可以有效提高修正结果的可信度。最后，文中通过一个数值质量－弹簧系统和一组试验钢板验证了所提出方法的可行性和可靠性。

1 区间响应面模型

1.1 区间扩张问题

区间数的运算法则（包括加、减、乘、除）和传统数学算法非常不同［11］，导致在区间反问题的求解过程中直接进行区间运算非常困难，比如计算区间函数的梯度。因此，当前绝大多数研究仍然在确定性框架下进行求解，并非完全意义上的区间模型修正。此外，区间运算过程中的区间扩张现象始终存在，很大程度上降低了修正结果的可信度。举例来说，定义函数f（x），g（x）和h（x）如下

可以看到，3个函数从传统数学理论上来说是完全一样的，仅表达式不同而已。若将函数中的变量x用区间数xI＝ ［0，1］表示，此时通过区间数运算可得

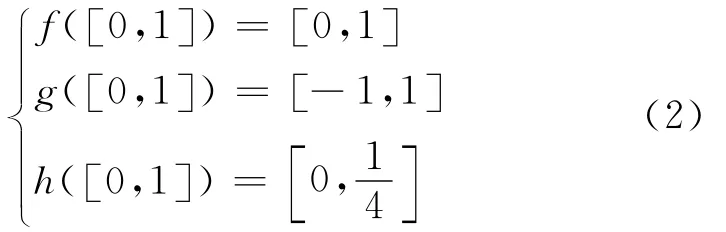
可见3个函数求解得到的区间值完全不同，其中仅h（x）给出了正确解，而其他2个函数都出现了区间扩张现象。这是由于x在f（x）和g（x）表达式中出现了2次，在运算过程中被认为是2个独立变量所造成的。因此，文献［15］提出了顶点法来解决这个问题。但如前所述，顶点法在复杂问题上的应用有着很大局限性，因此有必要寻求更为通用的求解方法。

1.2 区间响应面建模

本文将传统响应面模型和区间算法相结合，提出了IRSM的概念。传统的响应面模型实际上是一种显式的多项式数学表达式，可以将系统的参数x和响应y联系起来［18］

式中β为常系数，通过对函数近似误差ε的最小二乘估计来求解；k为参数个数；xi表示参数主效应，xixj表示参数间相互效应。式（3）为2阶响应面模型的完整表达式，其对大多数工程问题来说精度可以满足要求，因而得到了广泛应用［19］。而在构建IRSM过程中，需要对式（3）进行改造。首先要忽略掉相互效应项，因为大多数情况下，参数间相互效应对响应面模型总方差的贡献非常小［20，21］，忽略后并不影响模型的精度，反而还能提高求解效率。然后利用配方法将式（3）转化为完全平方项

这样可以使表达式中xi仅出现一次，从而在区间运算过程中避免了区间扩张现象的出现。最后，将xi用区间数表示，可以得到

式中 上标I表示区间数或区间变量。

式（5）即IRSM的理论表达式。利用该模型可以直接进行区间运算，以方便地求得响应yI的区间值，并在优化过程进行快速反向求解。

1.3 区间响应面和传统响应面的异同

本文提出的IRSM是建立在传统的2阶响应面模型基础上，通过对后者表达式的变换并引入区间数，得到IRSM表达式。该表达式的特点是每个区间参数都仅出现一次，以此有效避免区间运算过程中的区间扩张现象。此外，传统响应面仅能针对实数进行分析，而IRSM可以同时考虑区间数和实数，即将实数作为“点区间”来进行运算，这也是IRSM的优势之一。总体来说，这两种响应面类型之间既有联系，也有区别，同时二者的应用领域也有所不同。

2 区间模型修正过程

区间模型修正过程与传统的确定性修正有着很大不同，前者需要采用区间算法来处理区间变量。除了前述的IRSM，本文提出的区间模型修正方法还需要考虑的问题包括：1）参数和响应的选取；2）区间目标函数的建立；3）区间优化算法。

2.1 参数和响应的选取

选择合适的参数和响应是区间模型修正成功与否的关键一环。在结构参数方面，一般可以选取代表结构刚度和质量的参数，比如弹性模量、截面惯性矩、材料密度等。在响应的选择上，可以采用结构的静动力测量值如挠度、应变、频率、模态振型等作为目标响应，其中使用较多的是频率（特征值）和振型（特征向量）。测量频率要比振型简单得多，精度往往也更高。但振型包含了结构的空间信息，对损伤定位来说又是非常必要的，虽然考虑振型会使得区间模型修正问题变得更为复杂。同时要注意的是，需要根据具体的修正策略和方法来确定响应，比如顶点法就无法采用模态振型作为响应，这点可以通过理论推导来说明。

特征值对结构质量和刚度矩阵（元素）的偏微分可以表示为［22］：

式中 λ和φ分别表示特征值和特征向量；K和M表示结构的刚度和质量矩阵，其分块矩阵（或元素）为kj和mj。因为M和K分别为正定和半正定矩阵，所以式（6），（7）的符号在特定参数区间内不会发生变化，即满足单调性条件。因此，特征值区间的上下界容易通过刚度和质量元素的上下界值组合求得。对特征值而言，其偏微分可以表示为［17］

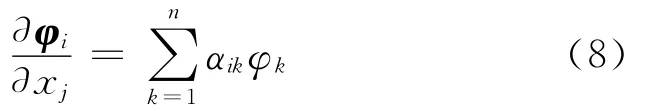
其中

由式（9）可见，由于λi－λk的正负号会发生变化，即αik的正负号会发生变化，使得式（8）的单调性条件无法得到保证。因此，刚度和质量元素的上下界值组合未必对应特征向量区间的上下界，导致顶点法不适用。但是若采用区间响应面模型进行修正，则不要求满足单调性条件，因此可以同时采用特征值和特征向量作为目标响应，这也是本文方法的主要优点之一。

2.2 区间目标函数

区间模型修正目标函数的构造与传统的确定性修正问题有所不同，前者不能直接采用区间响应相对误差的最小化来求解优化问题。举例来说，数值估计的区间响应yI＝ ［20 ，30］ 与实测响应区间＝［20，30］的相对误差应该为零。但对区间运算来说并非如此，比如：

由上式可见，在确定性模型修正中常用的目标函数表达式F1和F2，经过区间运算后，其相对误差值都不为零，因而不能直接用于区间模型修正中。有鉴于此，本文提出采用响应yI的上下界和来构建目标函数，即有

式中m表示响应的数目。

2.3 区间优化算法

构造目标函数后，即可以通过最小化F求解区间优化问题

每个迭代步中首先调整参数区间的大小；然后利用区间响应面模型快速计算结构响应区间，并与实测区间进行对比，若不符合收敛性要求，则重新调整参数区间大小，再次优化；反复进行上述调整直至F值小于预先设置的容差（tolerance），此时迭代过程收敛。要注意的是，优化过程要设置约束条件，即参数的下界x不能大于其上界，以保证修正参数区间的合理性。

在算法实现上，本文采用单目标优化方式，函数F中每阶响应在优化过程中的权重相同，并通过建立线性约束来设置参数变化的界限，最后通过二次规划算法求解F最小值的最优解。值得一提的是，待修正参数的初始区间范围（不确定性大小）可以设置较大，其对参数区间的最终估计精度影响很小。同时本文建议一次修正的参数数目不宜过多，因为响应面构建时所需的样本数会随着参数数目的增加而呈指数级增长，使得计算量大为增加。同时过多参数也容易导致优化过程出现病态问题，使得优化求解无法收敛或者降低了参数区间估计的精度。

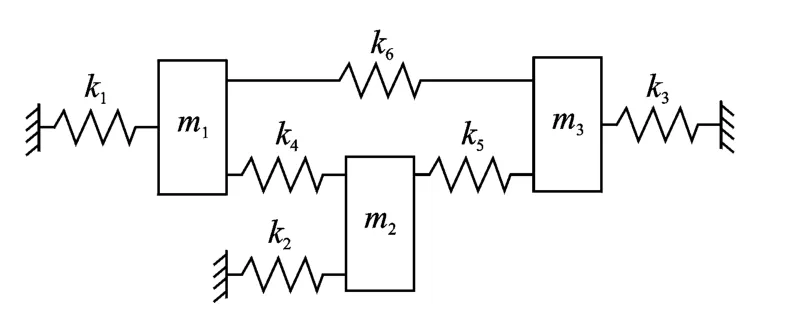
图1 3自由度质量－弹簧系统Fig.1 Three degree of freedom mass－spring system

3 数值算例

本文首先通过一个数值质量－弹簧系统来验证所提出的方法，如图1所示。系统由3个质量块和6组弹簧组成，其中假定k1，k2，k5为不确定的区间参数。各参数的真实值或区间如下所设：

本例中采用系统的3阶特征值λ1，λ2，λ3以及第一阶特征向量的第一分量绝对值φ（1，1）作为目标响应，对应地建立了4个IRSM，其中f1和φ（1，1）的表达式举例如下：

可以看到，表达式中的变量均为区间参数，因此区间运算可以直接在表达式上进行，以快速计算响应区间。同时可以基于上述模型，通过反向优化过程来估计参数区间。本例中3个待修正参数的初始区间设为k1＝k2＝k5＝ ［0.5，1.5］，修正后的结果列于表1。由表1可见，区间修正后参数的平均误差由初始的［37.5，25.0］%降低至［0.4，0.3］%，说明参数区间的估计是非常精确的。图2为系统特征值和特征向量的收敛图，可以看到预测的响应区间和实际区间吻合良好。由本算例分析结果可知，本文方法可以很好地估计不确定性参数的区间范围，并且可以同时采用系统特征值和特征向量作为目标响应，比顶点法的应用范围更广。此外，采用区间响应面模型替代有限元模型，可以快速方便地进行区间运算，有效地简化了区间优化问题的复杂程度，并提高了修正效率。

表1 质量－弹簧系统参数区间估计值Tab.1 Estimated parameter intervals of the mass－springsystem

图2 质量－弹簧系统响应区间收敛图Fig.2 Convergence plots of response intervals of the mass－spring system

4 试验验证

为了进一步验证所提出的方法，本文实测了一组共55块名义上完全相同的钢板，如图3所示。钢板名义几何尺寸为600mm（长）×120mm（宽）×3 mm（厚）；名义材料特性为杨氏模量210GPa，剪切模量83GPa，质量密度7 860kg／m3。试验中在钢板一端的两个角部（振幅最大处）各布置一个加速度传感器，并采用橡皮筋悬挂的方式模拟自由边界条件。然后对每块钢板进行锤击试验，同时测量锤击信号和响应信号，以获取测点处的频响函数，并提取钢板前5阶自振频率，用于区间参数识别。试验过程为了尽可能减少人为因素和环境因素的干扰，所有钢板都由同一个试验人员进行测试，采用完全相同的试验步骤和试验仪器，并且保证钢板的自由悬挂点和测试敲击点也完全相同。同时，试验在相对恒温的室内进行，以避免温差造成的频率变化。最后，由图4可见，在最终获取的钢板模态中，第1，2，4阶为弯曲模态，第3，5阶为扭转模态。

为了进行区间模型修正，首先采用壳单元建立钢板的有限元模型，沿钢板短边划分10个单元，长边划分30个单元，共得到300个壳单元，如图4所示。然后根据钢板的几何尺寸和材料特性名义值计算得到前5阶频率的区间中值为44.37，122.89，136.54，242.11及279.80Hz。而对5阶模态振型来说，弯曲模态主要由钢板厚度t和杨氏模量E控制；扭转模态主要由t和剪切模量G控制。考虑了扭转模态后，区间参数识别的难度增加，更能有效验证所提出方法的可靠性。

图3 钢板锤击试验Fig.3 Impact testing of the steel plates

图4 钢板有限元模型和振型Fig.4 The FE model and modal shapes of the plates

4.1 参数和响应的选取

本算例选取t，E，G作为待修正参数，主要考虑到：1）钢板在冷轧制造过程中，厚度t的变异性比长度和宽度大得多，因为切割钢板的时候长宽容易控制，而轧制过程则很难控制钢板厚度（仅3mm）的均匀性（见表2所示）。更重要的是，同样百分比的厚度改变所造成的钢板频率变化要比长宽改变所造成的大得多。2）对于钢材来说，由于材料的均质性，其材料特性是稳定的。但加工工艺等因素可能会导致钢板的材性呈现不均匀变化。

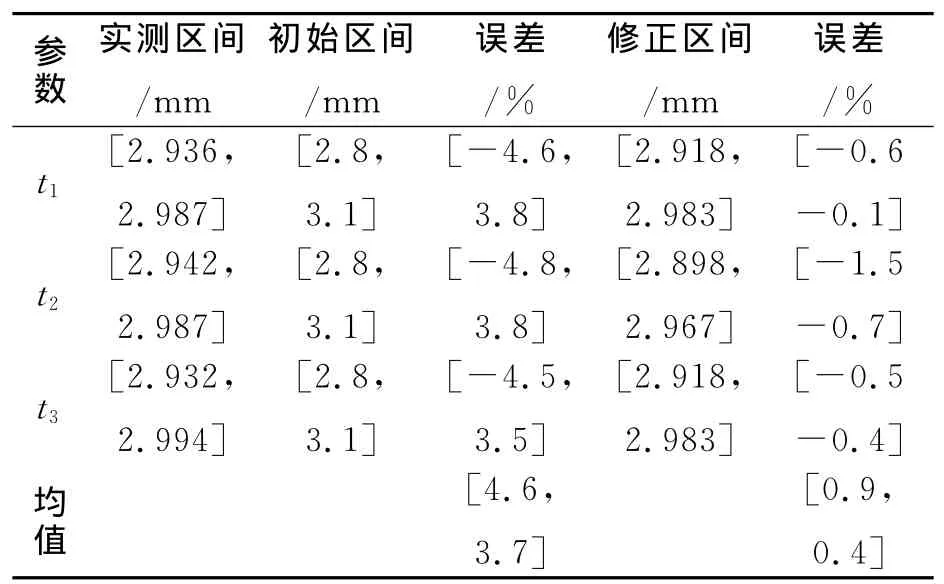
表2 厚度参数区间估计值Tab.2 Interval estimations of the thickness parameters

此外，考虑到频率的测量精度相对较高，本例中选取钢板的前5阶频率作为目标响应。由表3可见，对此类均质钢板来说，频率的不确定性很小，体现在实测频率的小区间范围上，因而对区间模型修正具有一定的难度。

表3 钢板频率区间修正值（厚度）Tab.3 Frequency intervals of the steel plates（thickness）

4.2 厚度t的区间识别

首先识别厚度t的区间范围。为了提高识别精度，将t沿板长边方向分为3个等分区域t1，t2和t3。试验前对每个区域的厚度用高精度千分尺测量2次并取平均值，进而得到55块钢板的厚度区间为t1＝ ［2.936，2.987］mm，t2＝ ［2.942，2.987］mm，t3＝ ［2.932，2.994］mm。

为了建立区间响应面模型并进行修正，t1，t2，t3的初始区间均设为［2.8，3.1］mm，然后对应于5阶频率分别建立了5个IRSM。以第1阶为例，其表达式如下

最后通过区间修正估计的参数区间值列于表2。由修正结果可见，厚度的估计值非常接近于实测值，绝对平均误差由初始的［4.6，3.7］%降至［0.9，0.4］%，说明区间优化过程没有发生区间扩张现象，修正精度高。此外，修正后的频率区间误差（见表3所示）也由初始的［4.2，4.0］%降低至［0.7，0.8］%，说明区间优化过程是收敛的，如图5所示。

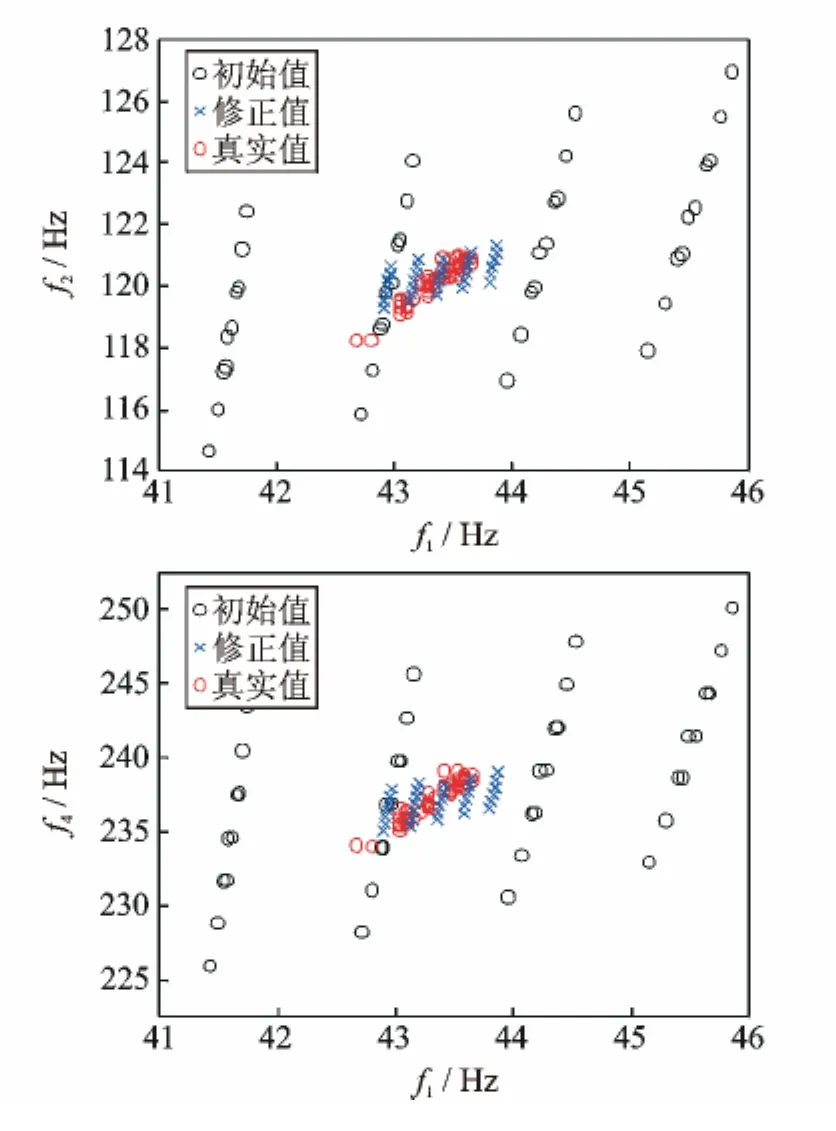
图5 钢板频率区间收敛图（厚度参数）Fig.5 Convergence plots of frequency intervals of the steel plates（thickness parameters）

4.3 材料参数的区间识别

本算例同时对材料参数E，G的区间值进行了识别，即认为钢板频率的不确定性主要由材料参数的变异性所引起的。试验中不可能对所有钢板进行取样，因此仅对几块钢板材料试样进行了单向拉伸试验，并根据试验结果设置了E，G的初始区间分别为E＝ ［190，220］GPa，G＝［77，89］GPa。随后建立了前5阶频率的IRSM，其中第1阶的表达式举例如下

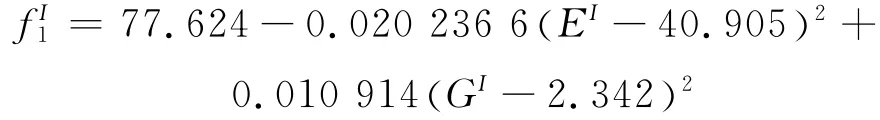
经过区间修正得到E，G的区间估计值分别为E＝［196.5，203.6］GPa，G＝［79.5，83.4］GPa，比初始区间大为缩小。二者的区间中值分别为200.1 GPa和81.5GPa，属于钢材材料特性的合理值，说明参数识别结果是合理的。修正后的频率区间误差（如表4所示）也由初始的［1.9，4.1］%降低至［0.4，0.2］%，说明区间优化过程是收敛的，如图6所示。

表4 钢板频率区间修正值（材料参数）Tab.4 Frequency intervals of the steel plates（material properties）

图6 钢板频率区间收敛图（材料参数）Fig.6 Convergence plots of frequency intervals of the steel plates（material parameters）

5 结 论

目前在模型修正领域，针对不确定性参数的非概率识别方法还很少，特别是基于区间分析的相关研究。本文将响应面模型和区间算法相结合，提出了区间响应面模型的概念，用于简化区间模型修正过程，以避免区间扩张问题并提高修正效率。所提出的方法可以精确识别一个数值质量－弹簧系统的弹簧刚度区间范围，同时也能很好地识别出一组试验钢板的几何及材料参数的变异性区间。本文的研究可以得到以下结论：

1）利用IRSM可以快速、方便地估计结构响应的区间，同时还有利于区间优化反问题的求解，避免了区间扩张现象和参数灵敏度的计算，大幅简化了优化过程并提高了修正效率。

2）区间响应面模型修正过程可以同时采用特征值和特征向量作为目标响应，不要求参数－响应的单调性关系，因此比顶点法的应用范围更广泛。

3）区间响应面模型修正所需的目标函数可以根据响应的上下界建立，而非直接采用区间数，以此避免区间运算导致的误差。

4）所提出的方法为区间模型修正技术提供了一个新的问题解决途径。

［1］ Friswell M I，Mottershead J E.Finite Element Model Updating in Structural Dynamics［M］.Kluwer Academic Publishers，Dordrecht，Netherlands，1995.

［2］ Fang S E，Perera R，Roeck G D.Damage identification of a reinforced concrete frame by finite element model updating using damage parameterization ［J］.Journal of Sound and Vibration，2008，313：544—559.

［3］ Alvin K，Oberkampf W，Diegert K，et al.Uncertainty quantification in computational structural dynamics：a new paradigm for model validation［A］.Proceedings of the 16th International Modal Analysis Conference［C］，1998：1 191—1 197.

［4］ 冯新，李国强，周晶.土木工程结构健康诊断中的统计识别方法综述［J］.地震工程与工程振动，2005，25（2）：105—113.Feng Xin，Li Guoqiang，Zhou Jing.State－of－the－art of statistical identification for structural health diagnosis in civil engineering ［J］.Earthquake Engineering and Engineering Vibration，2005，25（2）：105—113.

［5］ Moens D.A non－probabilistic finite element approach for structural dynamic analysis with uncertain parameters［D］.Catholic University of Leuven，Belgium，2002.

［6］ Friswell M I.The adjustment of structural parameters using a minimum variance estimator［J］.Mechanical Systems and Signal Processing，1989，3 （2）：143—155.

［7］ Beck J L，Katafygiotis L S.Updating models and their uncertainties.I：Bayesian statistical framework ［J］.Journal of Engineering Mechanics.1998，124 （4）：455—461.

［8］ 韩芳，钟冬望，汪君.基于贝叶斯法的复杂有限元模型修正研究［J］.振动与冲击，2012，31（1）：39—43.HAN Fang，ZHONG Dongwang，WANG Jun.Complicated finite element model updating based on Bayesian method ［J］.Journal of Vibration and Shock，2012，31（1）：39—43.

［9］ Khodaparast H H，Mottershead J E，Friswell M I.Perturbation methods for the estimation of parameter variability in stochastic model updating［J］.Mechanical Systems and Signal Processing，2008，22（8）：1 751—1 773.

［10］王登刚，秦仙蓉.结构计算模型修正的区间反演方法［J］.振动工程学报，2004，17（2）：205—209.Wang Denggang，Qin Xianrong.Interval method for computational model updating of dynamic structures［J］.Journal of Vibration Engineering，2004，17（2）：205—209.

［11］Moore R，Kearfott R，Cloud M.Introduction to Interval Analysis［M］.Society for Industrial and Applied Mathematics，Philadelphia，2009.

［12］Rao S S，Berke L.Analysis of uncertain structural systems using interval analysis ［J］.AIAA Journal，1997 35（4）：727—735.

［13］Li S L，Li H，Ou J P.Model updating for uncertain structures with interval parameters［A］.Asia－Pacific Workshop on Structural Health Monitoring［C］.Yokohama，Japan，2006.

［14］Jiang C，Han X，Liu G.R.Optimization of structures with uncertain constraints based on convex model and satisfaction degree of interval［J］.Computer Methods in Applied Mechanics and Engineering，2007，196：4 791—4 800.

［15］Dong W，Shah H.Vertex method for computing functions of fuzzy variables［J］.Fuzzy Sets and Systems，1987，24（1）：65—78.

［16］Qiu Z P，Wang X J，Friswell M I.Eigenvalue bounds of structures with uncertain－but－bounded parameters［J］.Journal of Sound and Vibration，2005，282（1）：297—312.

［17］Khodaparast H H，Mottershead J E，Badcock K J.Interval model updating with irreducible uncertainty using the Kriging predictor ［J］.Mechanical Systems and Signal Processing，2011，25（4）：1 204—1 226.

［18］Myers R H，Montgomery D C，Anderson－Cook C M.Response Surface Methodology：Process and Product Optimization Using Designed Experiments［M］.3rd Edition，New York：John Wiley ＆Sons，2009.

［19］Cundy A L.Use of response surface metamodels in damage identification of dynamic structures［D］.Virginia Polytechnic Institute and State University，2002.

［20］Fang S E，Perera R.A response surface methodology based damage identification technique［J］.Smart Materials and Structures，2009，18（6）：065009.

［21］Fang S E，Perera R.Damage identification by response surface model updating using D－optimal design［J］.Mechanical Systems and Signal Processing，2011，25（2）：717—733.

［22］Fox R，Kapoor M.Rates of change of eigenvalues and eigenvectors ［J］.AIAA Journal，1968，6（12）：2 426—2 429.