旋转复合材料薄壁轴的自由振动与稳定性＊

任勇生，代其义，张兴琦

（山东科技大学机械电子工程学院，山东 青岛266590）

引 言

在包括能源、航空和汽车在内的许多工业技术领域内，广泛地存在着一类旋转柔性细长结构，它的转动角速度矢量与其结构的纵轴保持平行，在能量传动过程中发挥着无可替代的重要作用，力学上通常将其称之为旋转轴。例如燃气轮发电机传动轴、航空发动机传动轴以及汽车后轮驱动轴等等。

纤维复合材料由于比强度和比刚度高、抗疲劳和减振性能好，在直升机尾传动轴［1］以及汽车传动轴［2］的结构设计中已经显示出广阔的应用前景。采用轻质纤维复合材料取代传统的金属材料不仅可以减轻结构的重量，同时还能够减少噪声、提高结构的抗振性能［3］。然而由于纤维复合材料力学性能的各向异性，加之轴的设计一般采取薄壁结构形式，因此在轴向拉伸、横向弯曲以及扭转变形之间，存在着显著的弹性耦合。精确地分析复合材料轴的振动特性是对其稳定性评估和参数优化设计的基础。传统的基于各向同性假定的金属材料轴的动力学模型与分析方法显然已经不再适合于各向异性复合材料传动轴，因此，需要建立更为先进的模型来指导复合材料轴的动力学设计。

迄今为止，在实心梁（Euler－Bernolli梁和Timshenko梁）理论、圆柱壳理论和薄壁梁理论的框架下，人们已经提出了复合材料轴的一些动力学分析模型。文献［4］将Timoshenko梁理论和Donnell薄壳理论结合在一起，建立旋转复合材料轴的刚度矩阵并采用有限元方法导出系统的运动方程，由此计算了薄壁复合材料轴的临界转速。文献［5］基于等效模量梁理论（Equivalent modulus beam theory，EMBT）对复合材料轴进行了动力学建模，并且将临界转速的理论结果与实验结果进行了对比。文献［6］分别基于EMBT和分层梁理论（Layerwise beam theory，LBT）建立复合材料轴的动力学模型，研究发现对于非对称铺层方式，采用两种模型得到的临界转速存在偏差。文献［7］依据壳的一阶近似理论推出了薄壁复合材料传动轴的运动微分方程。并且应用该模型分析计算了不同类型的复合材料传动轴的临界转速。文献［8］采用Timoshenko梁理论建立了复合材料传动轴的动力学方程。该模型考虑了陀螺效应和弯扭耦合的影响。文献［9］根据Timoshenko梁理论和Hamilton原理推导了旋转复合材料锥形轴的动力学方程。研究发现锥度比对轴的固有频率有显著影响。文献［10］基于一阶剪切梁理论提出了一个复合材料轴系统的有限元动力学模型，该模型除了轴还包含了刚盘以及轴承。文献［11］和［12］基于Rehfied的复合材料薄壁梁理论［13］，建立了复合材料轴的振动微分方程，研究了矩形截面轴和圆形截面轴的固有频率和稳定性特性，其中包括横向剪切的影响。

变分渐进法（Variational asymptotic method，VAM）［14］是从二维壳能量函数出发，采用渐进分析建立的一种精细的复合材料薄壁梁理论，与其他薄壁梁理论相比，它的主要特点在于其位移场表达式除了包含经典的扭转翘曲之外，同时还包含由于轴向拉伸以及横向弯曲变形引起翘曲。VAM复合材料薄壁梁理论不仅适用于单闭室复合材料薄壁梁，而且也适用于含有多个闭室的复合材料薄壁梁。自上世纪90年代VAM复合材料薄壁梁理论问世以来，国外一些学者已经将其成功地应用于先进直升机复合材料叶片的结构建模和动力学分析［15－16］。然而，迄今为止，作者还没有见到将VAM复合材料薄壁梁理论用于复合材料轴动力学分析的研究报道。此外，大家也注意到，现有的VAM复合薄壁梁理论尚未考虑横向剪切变形的影响。

本文从VAM复合材料薄壁梁理论出发［14］，提出了一个旋转复合材料轴的动力学分析模型，其中引入了横向剪切变形的影响。基于Hamilton原理推导出复合材料传动轴的振动偏微分方程组。采用Galerkin法求解得到耦合振动固有频率和临界转速的近似解，并且给出了算例验证。采用本文建立的模型计算方法，计算和分析了周向均匀刚度配置（CUS）［12］复合材料传动轴的动力学特性。通过数值计算揭示了铺层角、旋转速度、长径比、径厚比以及横向剪切对复合材料传动轴自由振动固有频率和稳定性的影响。

1 振动微分方程的建立

图1表示长度为L的、绕其轴线以定常角速度Ω旋转的封闭截面纤维复合材料薄壁梁。旋转坐标系为（x，y，z），局部坐标系为（x，s，ξ），其中环向坐标s沿着薄壁梁中面切线逆时针方向，ξ沿着薄壁梁中面法线方向。

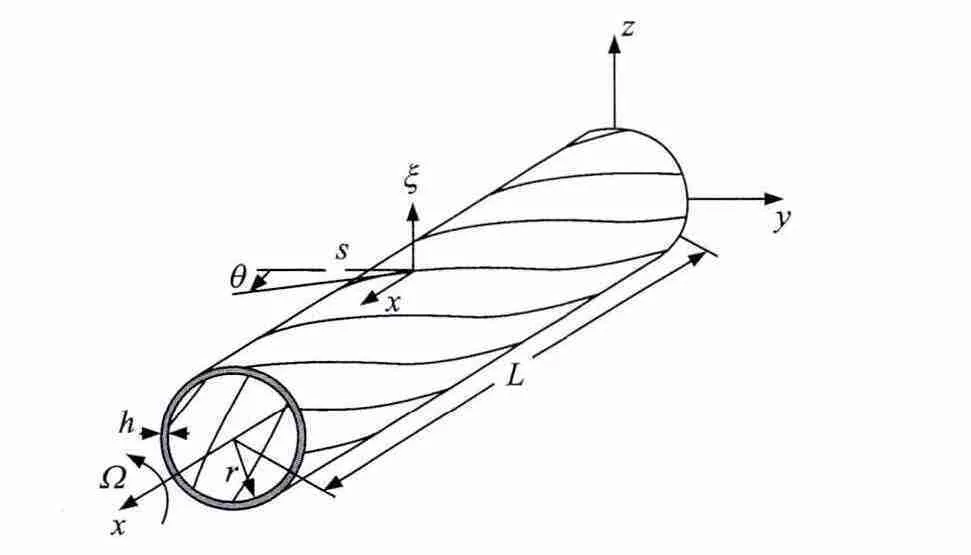
图1 圆截面复合材料薄壁轴Fig.1 Composite thin－walled shaft of a circular cross section

从文献［14］的位移场表达式出发，进一步引入横向剪切变形的影响，于是薄壁轴横截面上的任意一点沿着x，y，z方向的位移假设如下

式中U1（x，t），U2（x，t），U3（x，t）分别表示横截面沿着x，y，z方向的刚体位移；φ（x，t），θy（x，t），θz（x，t）分别表示横截面绕x轴的扭转角以及绕y，z轴的扭转角。y，z表示横截面中心围线上的点的坐标，是环向坐标s的函数。

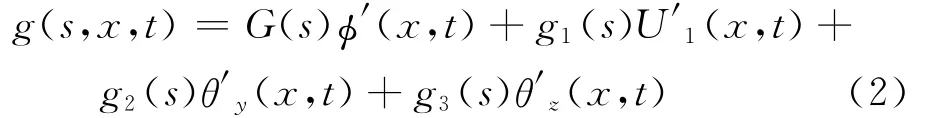
假定薄壁梁的翘曲函数g（s，x，t）具有如下形式上述等式右端的四项依次是与扭转、轴向拉伸、绕z轴弯曲和y轴弯曲有关的翘曲分量，其中G（s）的物理意义为扭转率，g1（s）的物理意义为轴向应变，g2（s）和g3（s）的物理意义为沿y，z方向的弯曲曲率。

在方程（1）和（2）中，θy（x，t），θz（x，t）可以表示如下

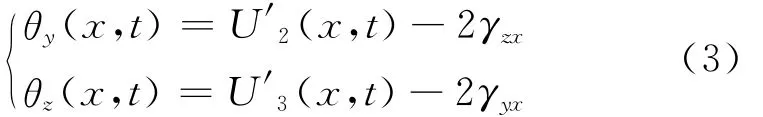
根据文献［14］几何方程，由位移方程（1）可以导出横截面正应变γxx和面内剪应变γxs的表达式，并且依照文献［17］，对横向剪应变γxξ的表达式也作出假设。因此，考虑剪切变形的薄壁轴的几何方程可以写成如下

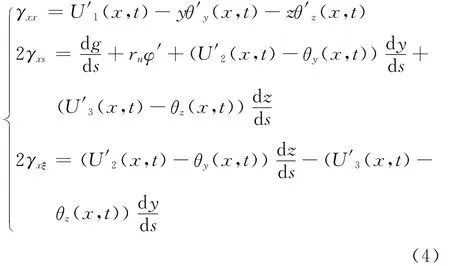
定义薄壁轴内力

薄壁轴内力－应变本构关系

其中

为了导出复合材料轴的振动方程，利用Hamilton原理

式中U和T分别为应变能和动能，分别由下式确定

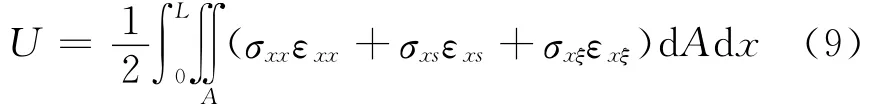
式中σxx，σxs，σxξ分别表示横截面正应力、面内剪应力和横向剪应力；εxx＝γxx，εxs＝2γxs，εxξ＝2γxξ是相应的工程应变。

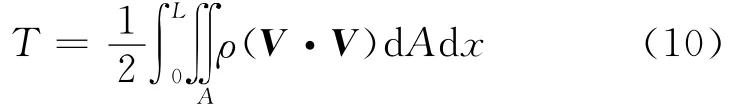
式中ρ表示材料密度，V表示变形后的梁上任意一点的速度矢量，它与变形梁任意一点的位置矢量：r＝（y＋u2）i＋（z＋u3）j＋（x＋u1）k之间满足关系：。

定义复合材料轴的轴力Fx，扭矩Mx，弯矩My和Mz，剪力Qy和Qz如下

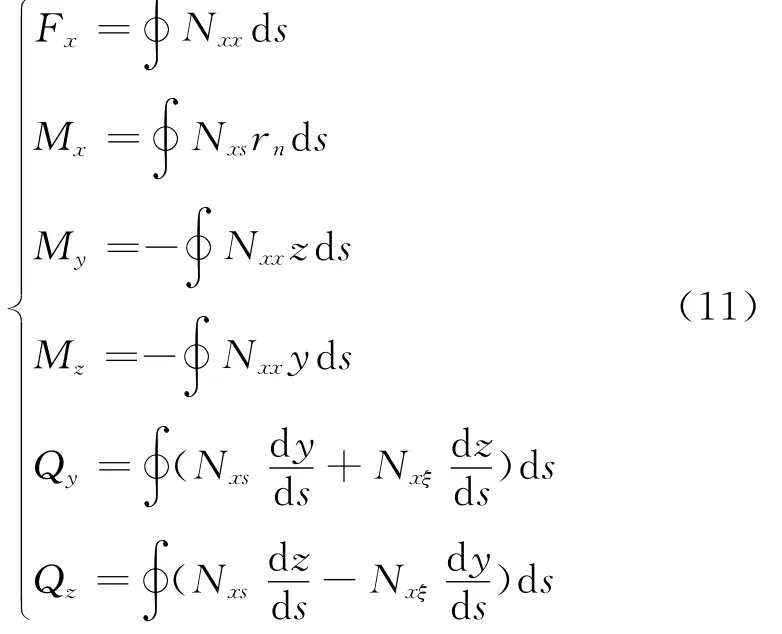
将式（6）代入式（11），并且利用几何方程（4），得

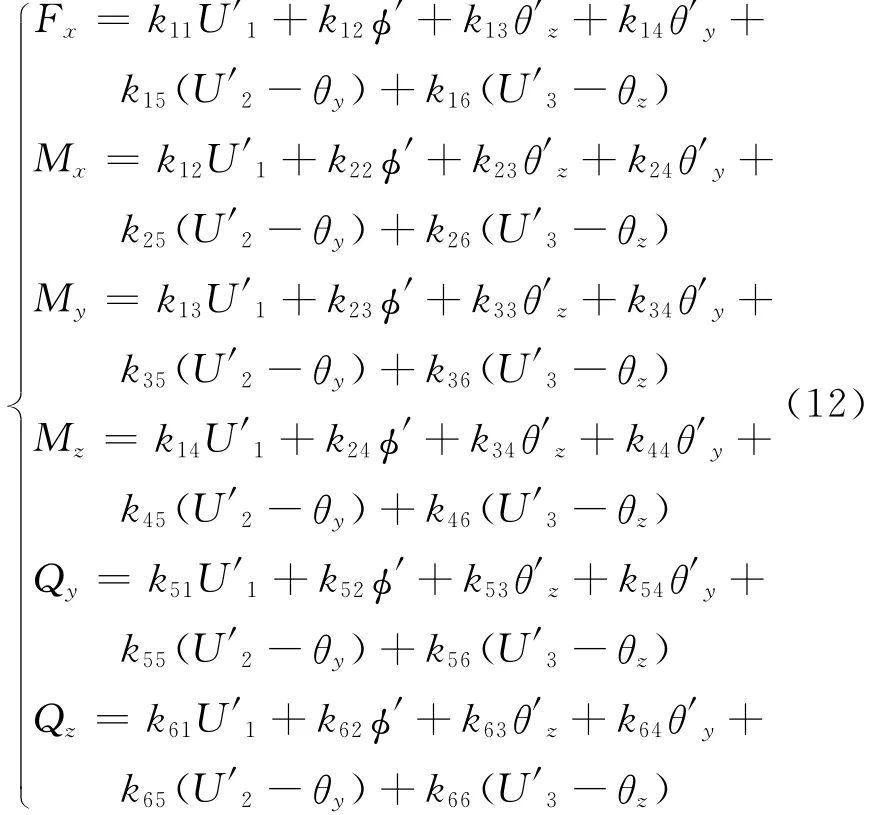
式中kij（i，j＝1，…，6）为复合材料轴横截面的刚度系数，具体表达式由于篇幅所限，不再列出。

通过比较可以发现，在全部的36个刚度系数kij（i，j＝1，…，6）中，其中的16个刚度系数kij（i，j＝1，2，…，4）的表达式与文献［14］中不计剪切变形的复合材料薄壁梁的刚度系数是一致的，而其余的20个刚度系数kij（i＝1，2，…，6；j＝5，6），kji（i＝1，2，…，4；j＝5，6）是由于计及剪切变形新增加的刚度系数。

假设复合材料轴具有周向均匀刚度配置（CUS）构型［12］，即满足

θ（y）＝θ（－y），θ（z）＝θ（－z）

式中θ表示由正向s轴进行度量的纤维铺层角。

将方程（9）和（10）代入（8），由 Hamilton原理可以导出运动方程如下

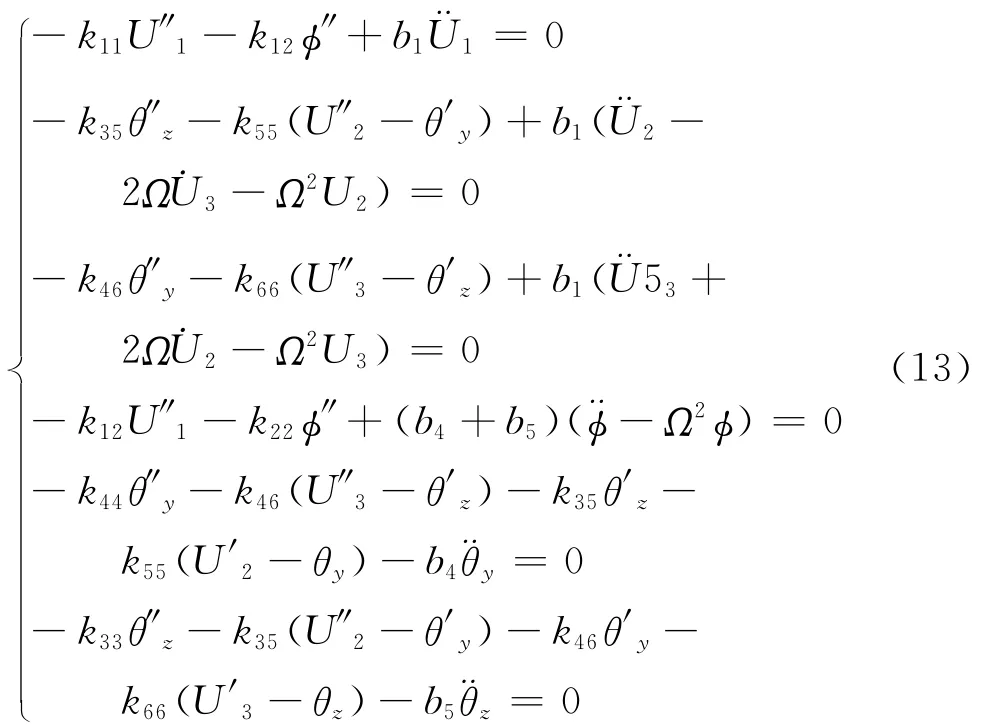
如果在方程（13）中的第二、三、五、六个方程中，令U″2－θ′y＝0，U″3－θ′z＝0，U′2－θy＝0，U′3－θz＝0，则可以导出不考虑剪切的复合材料轴的运动方程，此处不再写出。

方程（13）中的第二、三、五、六个方程，构成弯－剪耦合振动方程

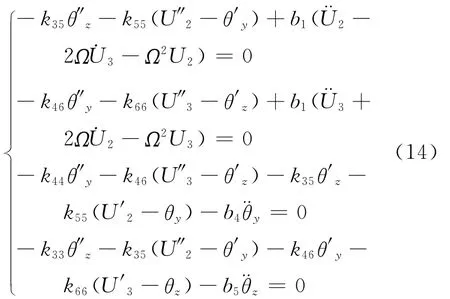
值得注意的是，在方程（14）中除了存在弹性变性产生的耦合，也存在由于刚性旋转产生的耦合，包括与转速一次方Ω相关的项，以及与转速平方Ω2相关的项。此外，在方程（13）中的第一和第四两个方程构成拉－扭耦合振动方程，此类耦合问题不在本文中进行讨论。

2 自由振动方程求解

假定弯曲位移U2（x，t），U3（x，t）和转角θy（x，t），θz（x，t）具有下列形式

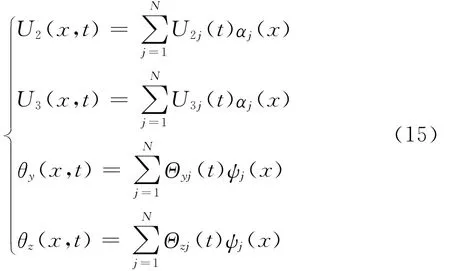
式中U2j（t），U3j（t），Θyj（t）和Θzj（t）表示广义坐标；αj（x）和ψj（x）表示轴的振型函数。

将方程（15）代入（14），采用Galerkin近似求解方法，得

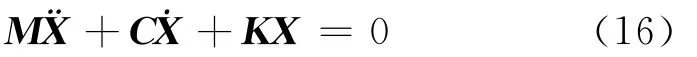
式中M为质量矩阵，C为旋转陀螺效应产生的阻尼矩阵，K为由弹性变形刚度与旋转引起的刚度叠加而成刚度矩阵

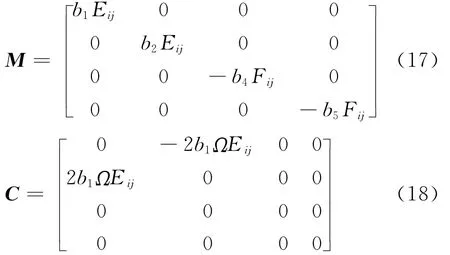
其中

广义坐标矢量表示为

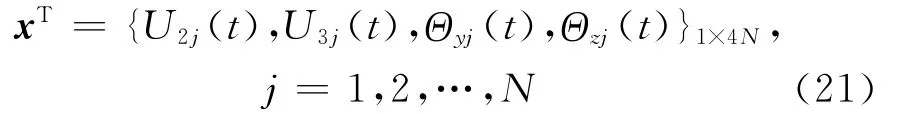
运动方程（16）可以进一步化为广义特征值问题

式中

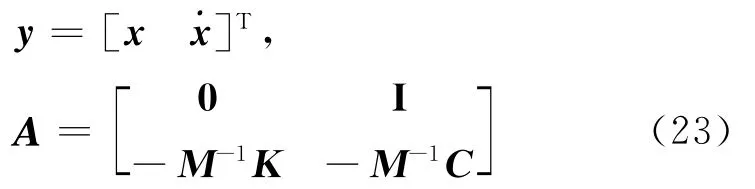
其中，0和I分别为零矩阵和单位矩阵。

3 数值结果与讨论

3.1 模型验证

算例1 为了检验本文建立的复合材料轴模型及其近似计算方法的正确性，下面首先针对一个石墨／环氧复合材料轴的固有频率特性，进行了数值方法的收敛性检验。轴的几何尺寸和材料参数分别取［12］：长度L＝2.023m，截面半径r＝0.127m，单层厚度h＝0.063 5mm，截面铺层方式为［θ］6；复合材料的性能参数为E1＝206.8GPa，E2＝E3＝5.17 GPa，G12＝3.1GPa，G23＝G13＝2.55GPa，ν21＝ν31＝0.006 25，ν32＝0.25，密度ρ＝1 528.15kg／m3。引入了标准化因子ω0＝138.85rad／s（表示非旋转轴在纤维铺层角θ＝0°的第一阶固有频率），则无量纲的固有频率和转速分别为ω＊＝ω×2π／ω0，Ω＊＝Ω×2π／（60ω0）。其中固有频率ω和转速Ω的单位分别为Hz和r／min。

表1表示两端简支轴的前六阶固有频率随振型函数个数N的变化情况，结果表明，本文提出的近似计算方法具有很好的收敛性，例如，为了获得前三阶固有频率，振型函数的个数只需取N＝6就可得到较高精度的结果（注：其中“－”表示大于保留最大模态个数N的高阶频率，由于已经超出了方程组（16）的阶数，所以没有结果显示）。

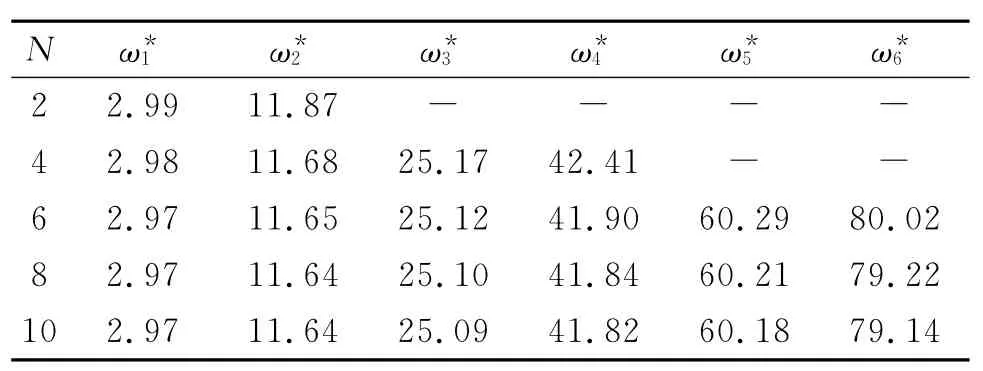
表1 模态个数对于固有频率的影响（Ω＊＝0，θ＝30°）Tab.1 Effect of model number Non natural frequencies（Ω＊＝0andθ＝30°）

表2表示不计剪切变形的悬臂复合材料轴的固有频率计算结果的对比，其中计算参数和无量纲化方法同文献［18］。由表2可以看出，本文结果与文献［18］结果符合得很好。

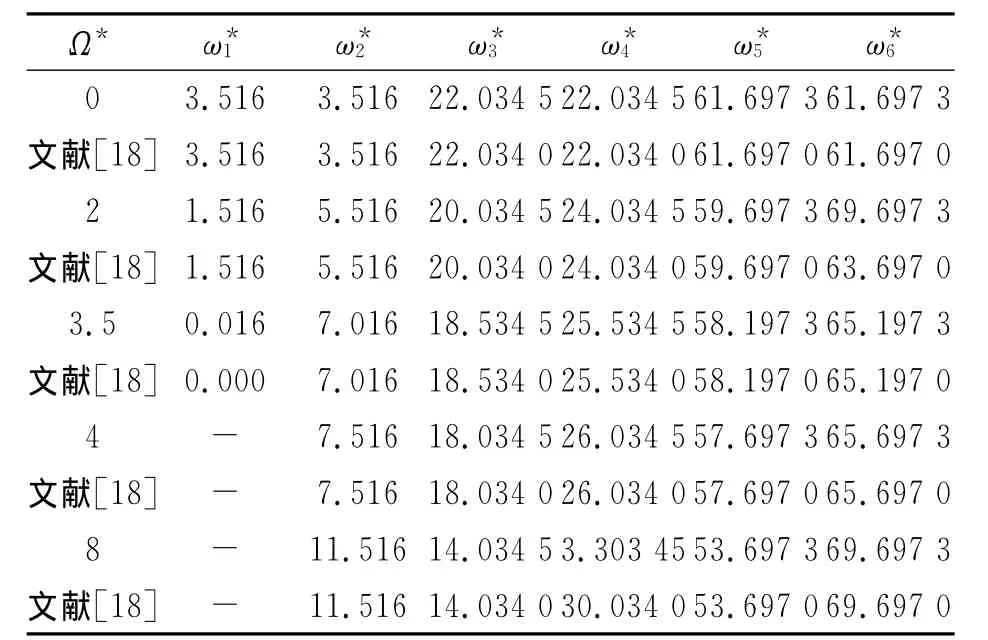
表2 不计剪切的悬臂复合材料轴的固有频率结果对比Tab.2 Comparison of the natural frequencies of a cantilevercomposite shaft without shear deformation

图2表示两端简支复合材料轴的固有频率随转速的变化曲线，其中考虑了剪切变形的影响。从图2可以看到，由于旋转的复合材料轴存在陀螺效应，所以固有频率在转速Ω＊≠0展示了分叉现象。其次，从图2还可以看到，针对四种不同的铺层角，本文结果与文献［12］的结果非常相近。

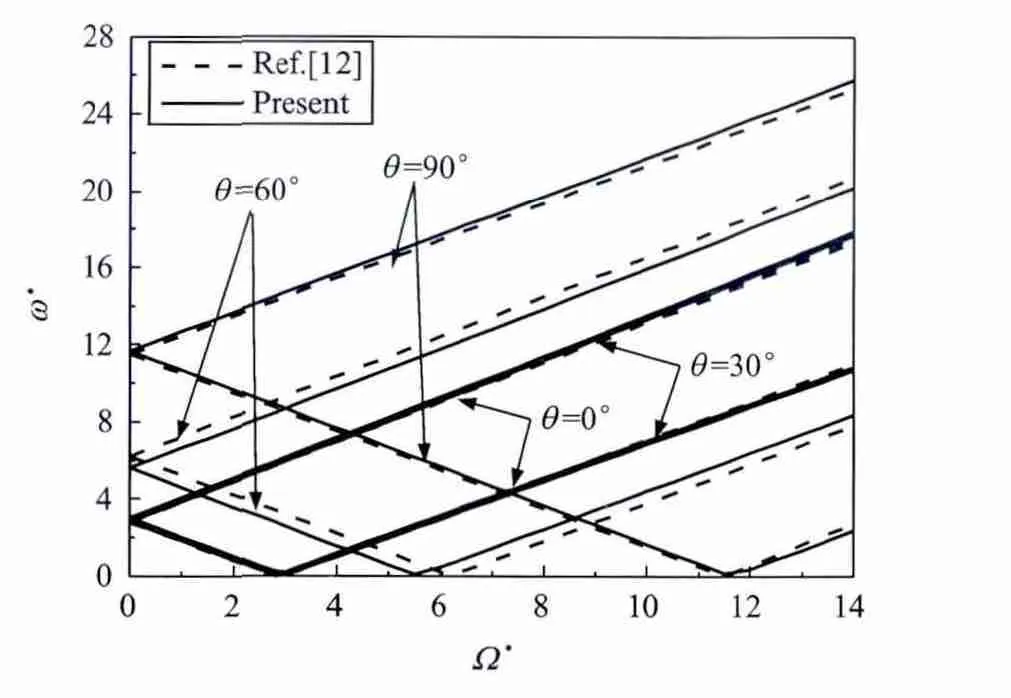
图2 不同铺层角的复合材料轴固有频率随转速的变化曲线Fig.2 The natural frequency of a simply supported composite shaft versus rotating speed for different ply angles

3.2 自由振动与稳定性分析

算例2 在下面的数值计算中，选取复合材料轴的几何尺寸为：长度L＝1.67m，截面半径r＝0.063 5m，单层厚度h＝0.132 1mm，截面铺层方式为［θ］8，轴的两端具有简支边界条件。弯曲振型和扭转振型函数的具体表达式见文献［8］和［9］。复合材料的性能参数如表3所示。

表3 复合材料性能参数Tab.3 Mechanical properties of composite material

图3表示复合材料轴的第一阶固有频率随转速的变化曲线。结果表明，当转速为0时，每个铺层角只对应于单独的一个固有频率，这是由于对于圆形截面轴而言，它在竖直（Z轴向）和水平方向（Y轴向）弯曲模态频率是相同的。随着转速的增加，由于旋转陀螺效应，固有频率曲线分叉为上下两支，上支随固有频率增加而增加，下支随固有频率增加而减少。分别称为上固有频率（Upper natural frequency，UNF）和下固有频率（Lower natural frequency，LNF），它们分别对应于惯性坐标系下的正进动频率和反进动频率。当LNF随转速的增加而减小至0时，所对应的转速称为临界转速Ω＊c；从图中还可以看出，无论是对于一阶模态还是二阶模态，临界转速都随着铺层角的增加而增加，最大的临界转速对应的铺层角θ为90°。这主要是由于当纤维铺设角沿轴的轴向铺层时，轴的弯曲刚度变为最大。

表4给出不计剪切和计入剪切时的复合材料轴的第一阶临界转速和第二阶临界转速的计算结果，由此可以看出，不计剪切的临界转速高于计及剪切的临界转速，并且两者的差别随着铺层角的增加而增加；在相同铺层角下，计及剪切和不计剪切的第二阶临界转速的相对误差要高于相应的第一阶临界转速的相对误差。例如在铺层角θ为90°时，这一误差由2.40%增加到9.43%。因此，在预测铺层角较大时的高阶临界转速时，剪切变形的影响尤其就显得十分重要。

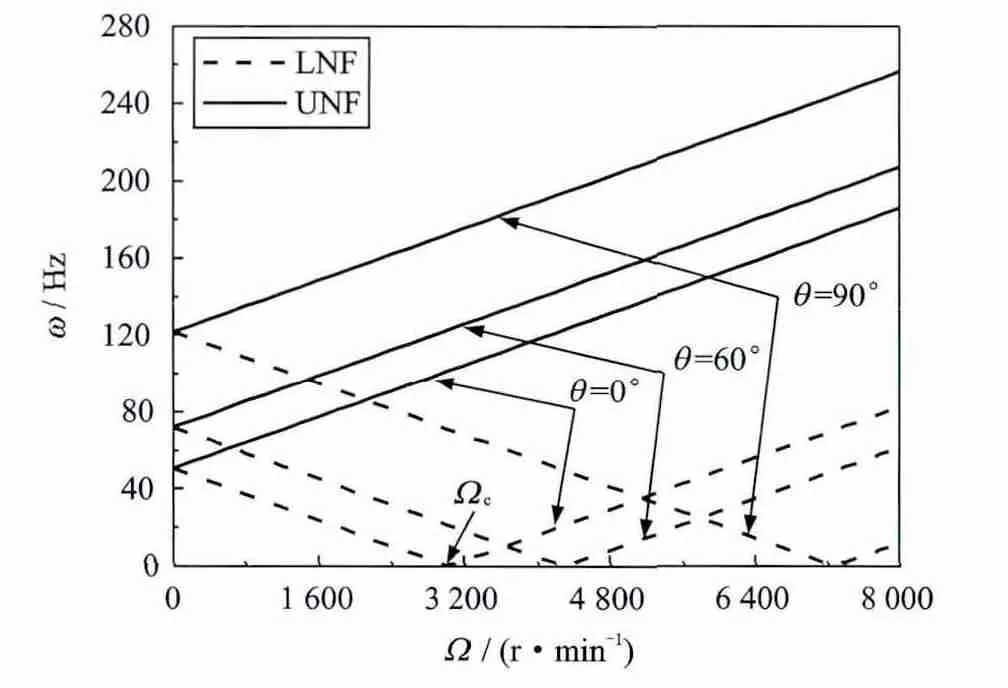
图3 不同铺层角复合材料轴的第一阶固有频率随转速变化曲线Fig.3 The first natural frequency of a composite shaft versus rotating speed for different ply angles

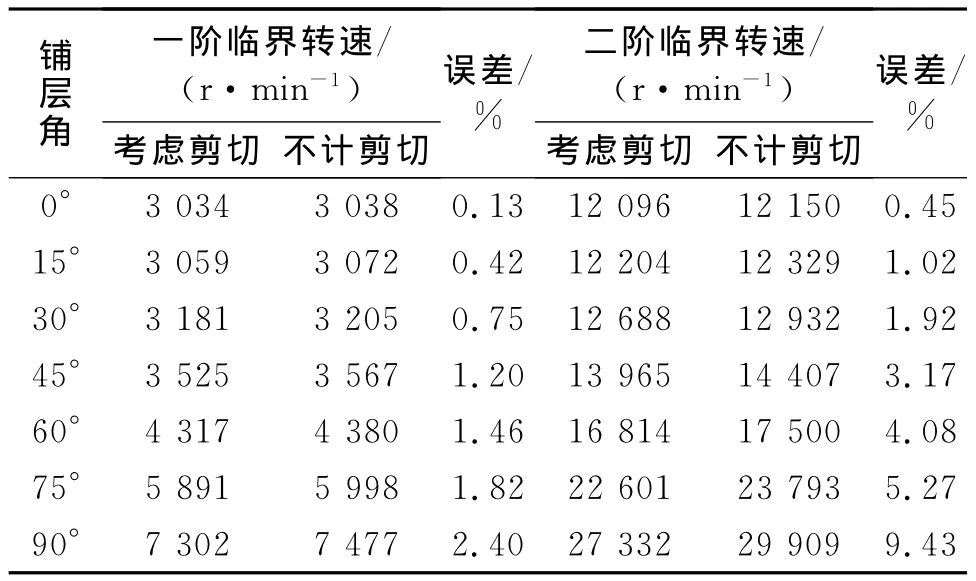
表4 计及剪切与不计剪切复合材料轴的临界转速Tab.4 The critical speed of a composite shaft with and without shear deformation

图4和5分别表示静止和旋转复合材料轴的前两阶固有频率随铺层角的变化曲线。结果表明，在静止状态下，轴的第一阶、第二阶模态所对应的UNF曲线和LNF曲线是重合的，它们都随着铺层角的增加而增加，这与前面的结论是一致的。另一方面，相对于第一阶固有频率，第二阶固有频率随铺层角的增加而增加的趋势更为明显；在旋转状态下的前两阶固有频率随铺层角的变化趋势和在静止状态的变化趋势是相同的，只不过此的UNF曲线和LNF曲线是分开的。

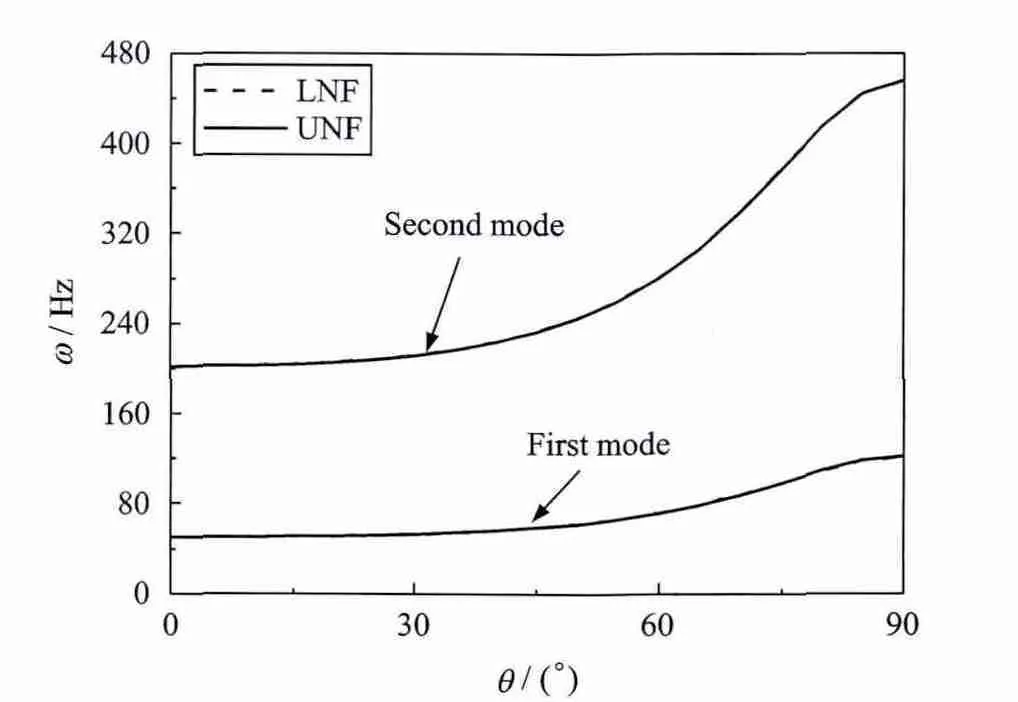
图4 复合材料轴前两阶固有频率随铺层角变化曲线（Ω＝0）Fig.4 The first two natural frequency of a simply supported composite shaft versus ply angle（Ω＝0）

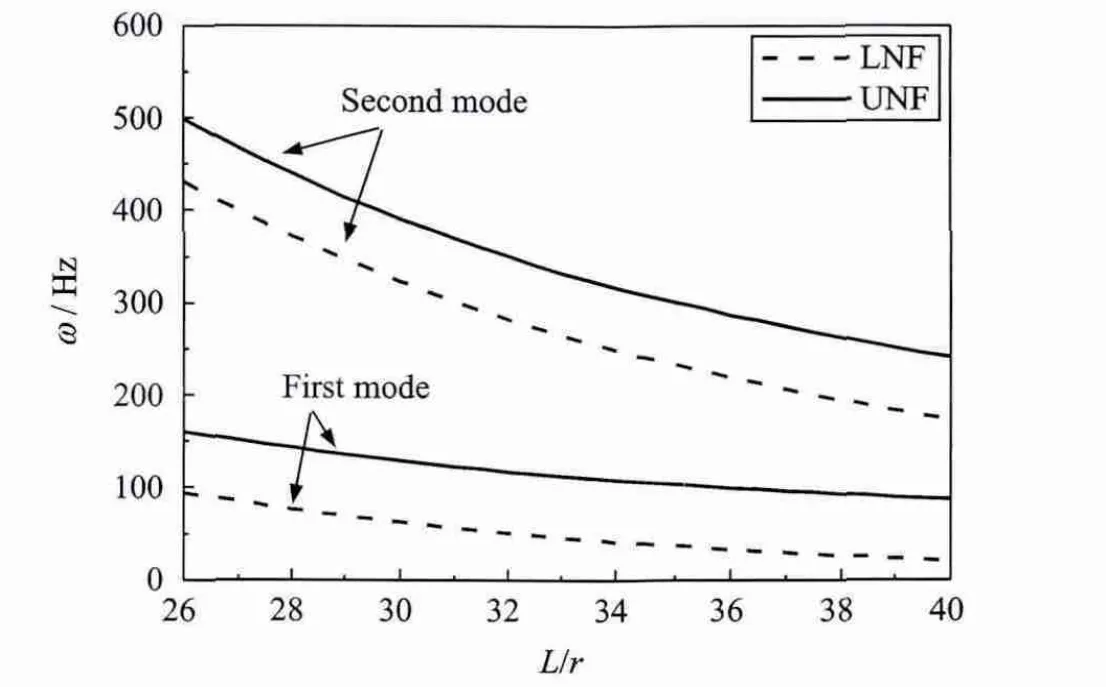
图6 复合材料轴的前两阶固有频率随长径比的变化曲线（Ω＝2 000r·min－1，θ＝90°）Fig.6 The first two natural frequencies of a composite shaft versus ratio of length over radius（Ω＝2 000 r·min－1，θ＝90°）

图6和7分别表示复合材料轴的前两阶旋转固有频率随长径比和径厚比的变化曲线。由图6可以看出，固有频率随着长径比的增加而减小；由图7可以看出，固有频率随着径厚比的增加而增加。

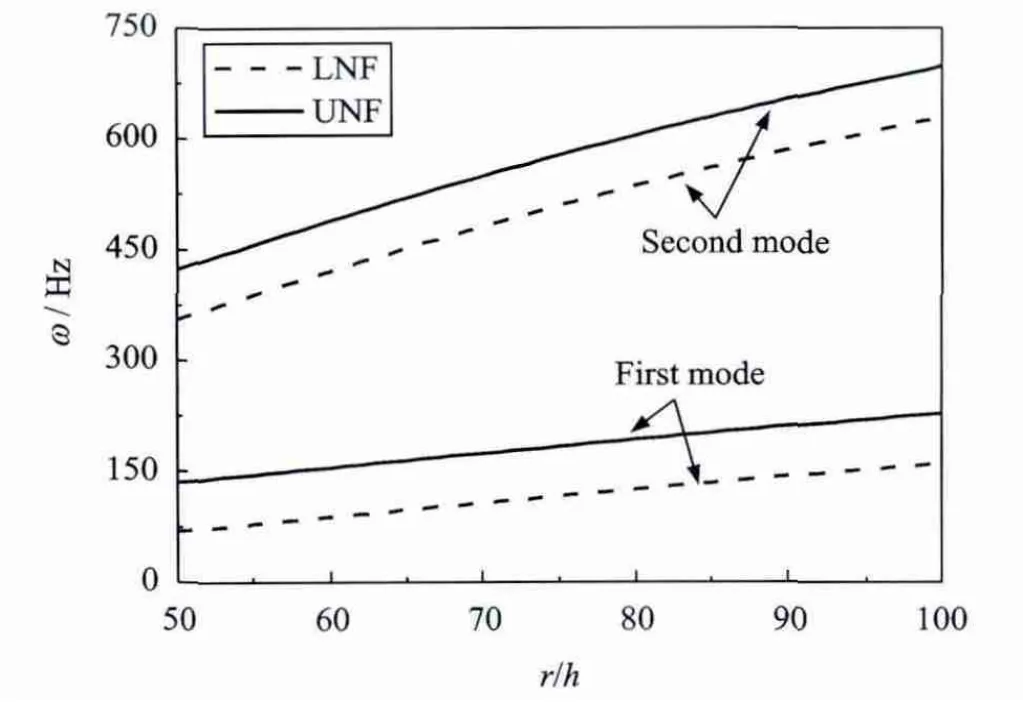
图7 复合材料轴的前两阶固有频率随径厚比的变化曲线（Ω＝2 000r·min－1，θ＝90°）Fig.7 The first two natural frequencies of a composite shaft versus ratio of radius over thickness（Ω＝2 000r·min－1，θ＝90°）

图8和9分别表示具有不同铺层角的复合材料轴的前两阶临界转速随长径比和径厚比的变化曲线。由图8和9可以看出，临界转速随着长径比的增加表现为减小的趋势，而随着径厚比的增加表现为增加的趋势。

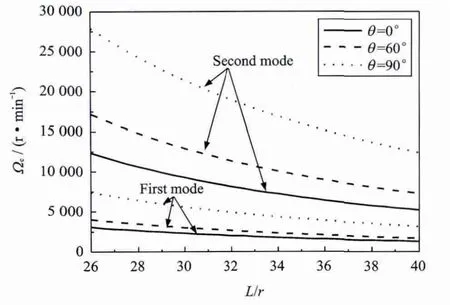
图8 复合材料轴前两阶临界转速随长径比的变化曲线Fig.8 The first two critical speeds of a composite shaft versus ratio of length over radius

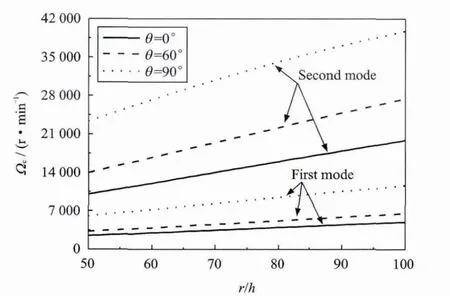
图9 复合材料轴两阶临界转速随径厚比的变化曲线Fig.9 The first two critical speeds of a composite shaft versus ratio of radius over thickness

4 结 论

本文基于复合材料薄壁梁理论建立了旋转轴的动力学模型。结构的位移场采用VAM模型进行描述，并且在其中引入了横向剪切变形的影响；采用Hamilton原理导出旋转轴的控制方程并采用Galerkin法对数学模型进行数值求解，获得旋转轴耦合振动的固有频率及其临界转速的近似分析解。本文模型的正确性通过收敛性分析以及与文献结果对比，得到了验证。采用本文建立的模型与计算方法，研究了旋转复合材料轴的自由振动与动力稳定性。数值结果表明：（1）当复合材料轴的铺层角或者径厚比增加时，固有频率随之增加；当复合材料轴的长径比增加时，固有频率随之减小，在轴的刚性旋转作用下，固有频率分叉为UNF和LNF曲线，其中UNF随转速的增加而增加，LNF随转速的增加而降低；（2）不计剪切变形的临界转速高于计入剪切变形的临界转速，并且两者的差别随着铺层角的增加而增加，在相同铺层角下，计及剪切和不计剪切的低阶临界转速的之间相对误差要高于相应的高阶临界转速之间的相对误差；（3）复合材料轴的临界转速随着铺层角或者径厚比的增加而增加；随着长径比的增加而减小。本文提出的模型可以为复合材料轴的动力学研究与设计，提供一种可供选择的分析理论与方法。

［1］ 王震鸣，杜善义，张衡，等.复合材料及其结构的力学、设计、应用和评价（第二册）［M］.哈尔滨：哈尔滨工业大学出版社，1998.Wang Zhenming，Du Shanyi，Zhang Heng，et al.Mechanics，design，application and evaluation of composites and structures（partⅡ）［M］.Haibin：Harbin Institute of Technology Press，1998.

［2］ Hetherington E L，Kraus R E，Darlow M S.Demonstration of a super critical composite helicopter power transmission shaft［J］.Journal of American Helicopter Society，1990，35（1）：23—28.

［3］ Faust H，Mack J，Spencer B.A composite rotor shaft for the Chinook［J］.Journal of the American Helicopter Society，1984，29：54—58.

［4］ dos Reis H L M，Goldman R B，Verstrate P H.Thinwalled laminated composite cylindrical tubes：Part IIICritical speed analysis［J］.Journal of Composites Technology and Research，1987，9：58—62.

［5］ Zinberg H，Symonds M F.The development of an advanced composite tail rotor drive shaft［A］.Presented at the 26th Annual National Forum of the American Helicopter Society［C］.June，Washington，DC，1970.

［6］ Singh S P，Gupta K.Composite shaft rotordynamic analysis using a layer wise theory［J］.Journal of Sound and Vibration，1996，191（5）：739—756.

［7］ Kim C D，Bert C W.Critical speed analysis of laminated composite hollow drive shafts［J］.Composites Engineering，1993，3：633—643.

［8］ Bert C W，Kim C D.Whirling of composite－material drivshafts including bending－twisting coupling and transverse shear deformation［J］.Journal of Vibration and Acoustics，1995，117：17—21.

［9］ Kim W，Argento A，Scott R A.Free vibration of a rotating tapered composite Timoshenko shaft［J］.Journal of Sound and Vibration，1999，226（1）：125—147.

［10］Chang M Y，Chen J K，Chang C Y.A simple spinning laminated composite shaft model［J］.Int.Journal of Solids and Structures，2004，41：637—662.

［11］Song O，Librescu L.Anisotropy and structural coupling on vibration and instability of spinning thinwalled beams［J］.Journal of Sound and Vibration，1997，204：477—494.

［12］Song O，Jeong N－H，Librescu L.Implication of conservative and gyroscopic forces on vibration and stability of an elastically tailored rotating shaft modeled as a composite thin－walled beam ［J］.J.Acoust.Soc.Am.，2001，109（31）：972—981.

［13］Rehfield L W.Design analysis methodology for composite rotor blades［A］.Proc.Seventh DoD／NASA Conf.on Fibrous Composites in Structural Design［C］.AFWAL－TR－85－3094，1985：1—15.

［14］Berdichevsky V，Armanios E，Badir A.Theory of anistropic thin－walled closed－cross－section beams［J］.Composites Engineering，1992，2：411—432.

［15］Cesnik C E S，Shin S J.On the modeling of integrally actuated helicopter blades［J］.International Journal of Solids and Structures，2001，38：1 765—1 789.

［16］Park J S，Kim J H.Design and aeroelastic analysis of active twist rotor blades incorporating single crystal macro fiber composite actuators［J］.Composites：Part B，2008，39：1 011—1 025.

［17］Song O，Librescu L.Structural modeling and free vibration analysis of rotating composite thin－walled beams［J］.Journal of the American Helicopter Society，1997：358—369.

［18］Banerjee J R，Su H.Development of a dynamic stiffness matrix for free vibration analysis of spinning beams［J］.Comput.Struct.，2004，82：2 189—2 197.