铣削建模中多种切削力模型的分析比较＊

杨毅青，张 斌，刘 强

（1.北京航空航天大学机械工程及自动化学院，北京100191；2.国防科技工业高效数控加工技术研究应用中心，北京100191）

引 言

铣削是最为普遍的一种金属切削加工方式。长期以来，人们对铣削加工过程中的动力学建模与仿真技术进行了大量的研究，以期对实际生产进行理论指导和工艺优化。切削力模型的选择与确定是铣削过程动力学仿真的基础。目前，线性切削力模型是使用最为广泛的一种，该模型中的六个切削力系数被视为与切削参数无关的固定常数［1］。线性切削力模型已被应用于各种铣刀的切削力建模及颤振稳定域仿真，并在实际中得到较好的验证［1，2］。ALTINTAS将该模型应用于平底立铣刀、球头刀与镶片刀等刀具的铣削动力学建模，切削力及颤振稳定域 预 测 与 实 验 吻 合 较 好［1］。INSPERGER［3］和DING［4］进一步完善了线性切削力模型下的铣削颤振稳定域预测，分别提出了半离散法与全离散法。线性切削力模型的不足之处是，对刃口力与瞬时切削厚度无关的假定不完全准确［5］；此外，由于切削力被表示成与切削厚度成线性关系，无法获取进给速度对颤振稳定域瓣的影响［6］。因此，人们在线性切削力模型的基础上对切削模型进行了拓展。

指数瞬时切削力模型是另一种较常见的模型，在该模型中切削力系数被表示成瞬时切削厚度的指数函数。张臣等研究了基于指数瞬时模型的球头铣刀切削力建模方法［7］。WAN以圆柱螺旋立铣刀为例，提出了一种仅需进行一次实验试切，即可根据瞬时切削力辨识指数瞬时模型系数的方法［8］。JENSEN建立了包含进给速度以及刀片几何参数的面铣削指数瞬时加工模型，实验结果表明颤振稳定域的临界切深随着进给速度的增加而增加［9］。MUNOA研究了基于指数切削力模型的铣削颤振稳定域预测，分析了进给速度对颤振稳定域的影响［10］。与线性切削力模型相对，指数瞬时模型是一种非线性模型，不但能准确预测切削力，而且能预测进给速度对颤振稳定域的影响。

相比以上两种切削力模型，针对其他模型的研究工作相对较少。尹力等建立了以进给速度、切深、主轴转速为自变量的铣削力系数多项式模型，并采用偏最小二乘回归方法辨识出切削力系数［11］。梁睿君等研究了以每齿进给量为变量的二次多项式切削力系数模型，揭示了主轴转速、进给速度与临界稳定切深之间存在非线性关系［12］。BUDAK研究了线性及指数平均切削力模型的切削力系数辨识及铣削建模技术，实验对比表明线性模型的精度高于指数平均切削力模型［5］。综合目前发表的文献，尚没有系统针对上述多种切削力模型在铣削动力学建模中的对比分析工作。据此，本文以圆柱螺旋立铣刀为例，围绕线性切削力模型、指数瞬时切削力模型、指数平均切削力模型以及一般多项式切削力模型的铣削动力学建模技术，分别对其中所涉及到的切削力系数辨识、切削力及颤振稳定域预测进行研究，并在此基础上系统总结各模型的优点与不足。

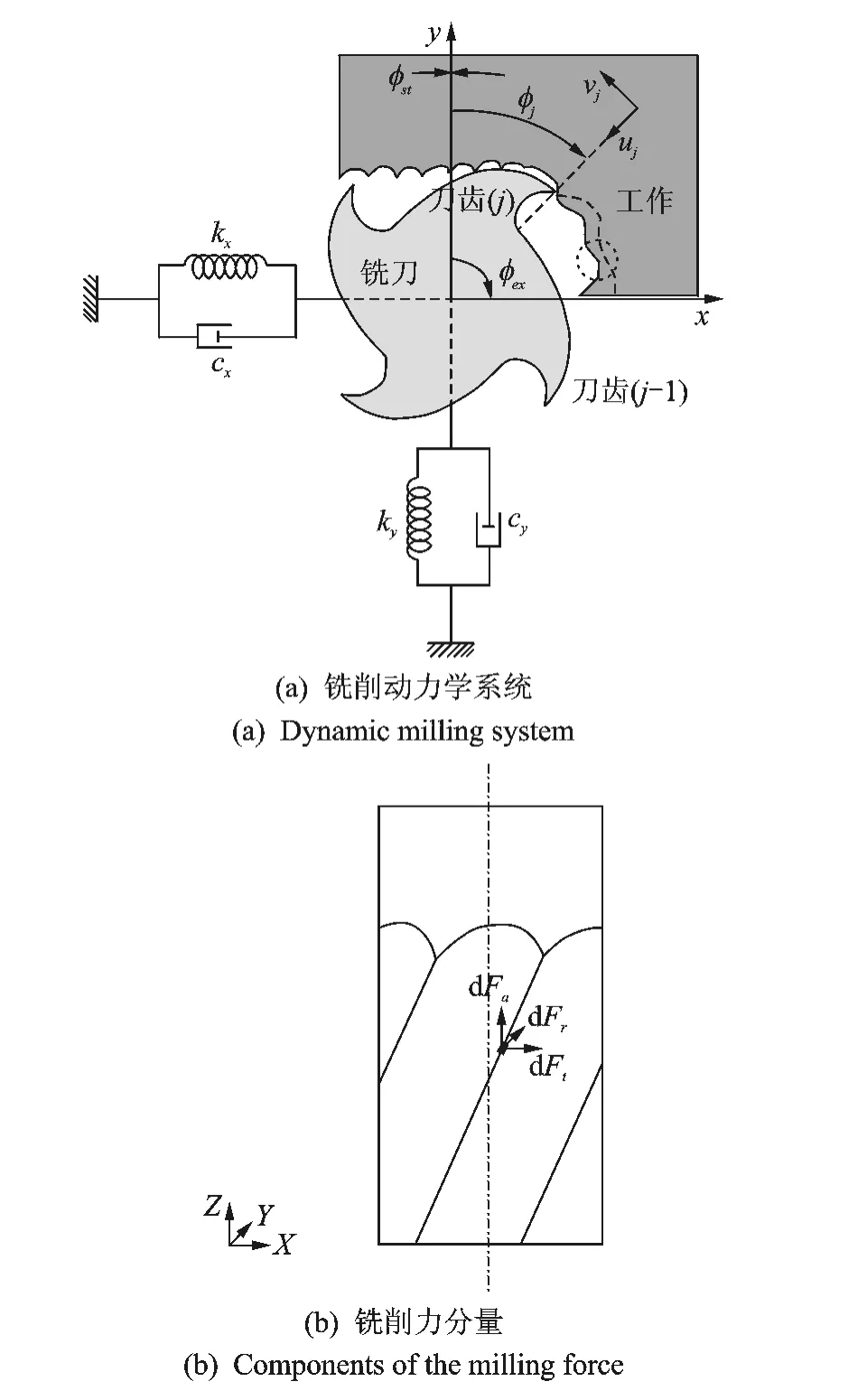
图1 铣削力分布示意图Fig.1 Modeling of the milling force

1 铣削过程建模

1.1 基本理论

以圆柱螺旋立铣刀为例（如图1（a）所示），将切削刃离散成若干微元。将每个微元上承受的切削力dF进行分解，可得切向力dFt、径向力dFr与轴向力dFa（如图1（b）所示）。微元分力的大小由刀具／工件材料性质、瞬时切削厚度与微元高度决定。通过座标变换，将切向、径向与轴向分力投影至机床坐标X，Y与Z方向，可得

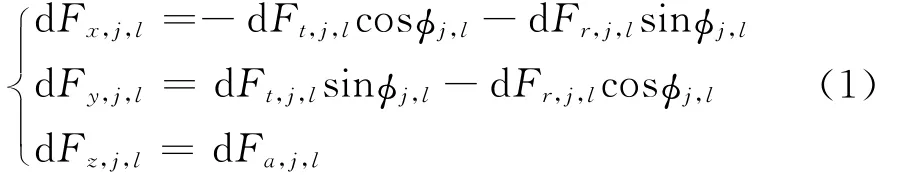
式中 dFx，dFy与dFz分别为切削力微元在X，Y与Z方向上的切削力投影分量；j代表切削刃l上的某一微元；φj，l为瞬时切入角。将任一时刻所有参与切削的微元上的力进行叠加，可得到铣刀沿X／Y／Z方向上的瞬时切削合力为

式中N为刀齿数，M为切削刃上所划分的微元数目。

1.2 铣削力模型分类

式（1）中，切削刃微元所承受的切向力dFt、径向力dFr与轴向力dFa可表述成下式

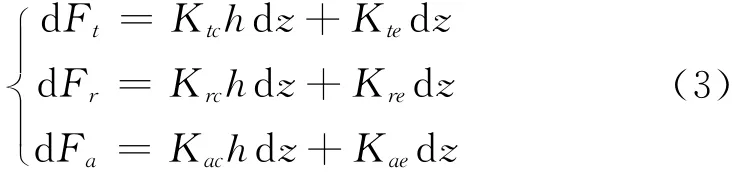
式中Ktc，Krc，Kac分别为切向、径向、轴向力系数；Kte，Kre，Kae分别为切向、径向、轴向刃口力系数；dz为切削刃微元高度；h＝csinφj，l为瞬时切屑厚度，c为每齿进给量。根据目前文献，切削力模型主要包括线性、指数瞬时、指数平均以及一般多项式。各模型下的切削力系数表达式如表1所示。

表1 切削力模型分类Tab.1 Categories of the cutting force model

2 铣削力系数辨识

2.1 铣削力系数辨识算法研究

对所有切削力模型而言，切削力系数辨识是铣削过程建模技术的关键。通过计算刀具一个旋转周期内的平均铣削力FA，可对切削力系数进行辨识。由于切削力系数的大小取决于刀具、工件等物理属性，不受切入、切出角的影响，为简化推导过程，在以下辨识过程中均以槽铣加工（φst＝0，φex＝π）为例。

1）线性切削力模型

计算刀具旋转周期内的平均切削力FA（FA，q＝Bqc＋Aq，q＝x，y，z）

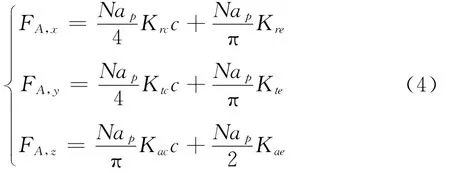
等式两边除以Nap，以c为变量采用最小二乘法进行拟合，具体推导过程可参考文献［1］。辨识出的切削力系数计算公式如下

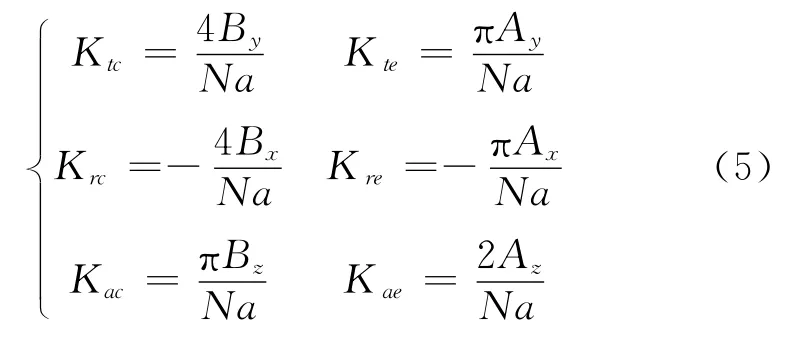
2）指数瞬时切削力模型

计算获得X／Y／Z方向上的每齿平均铣削力为

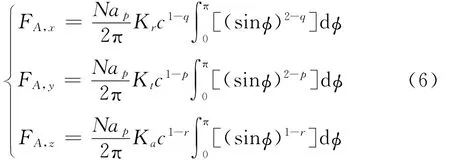
等式两边除以Nap并取对数，得到以lnc为自变量的线性表达式（ln（FA，q／Nap）＝Bqlnc＋Aq，q＝x，y，z）。采用最小二乘法进行拟合，可获得切削力系数计算公式如下

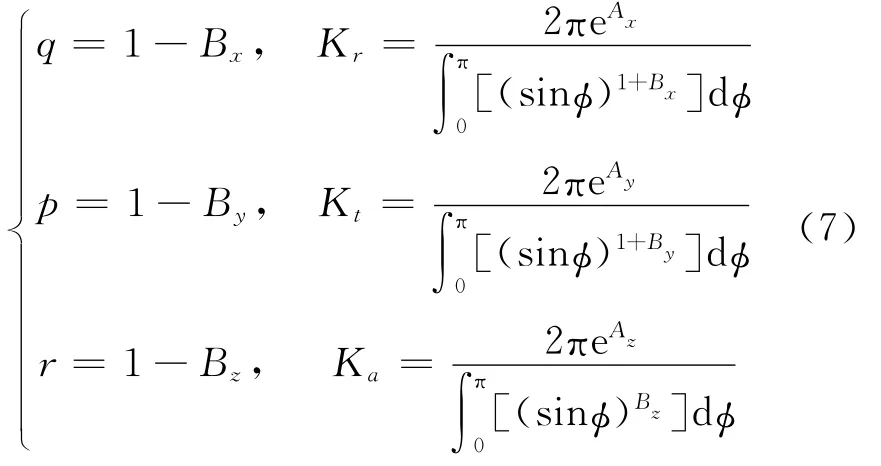
3）指数平均切削力模型

槽铣时，每转的平均切削厚度hA＝2c／π。计算获得X／Y／Z方向上的每齿平均铣削力为

等式两边除以Nap再取对数，得到以lnc为自变量的线性表达式（ln（FA，q／Nap）＝Bqlnc＋Aq，q＝x，y，z）。采用最小二乘法进行拟合，可得切削力系数计算公式如下

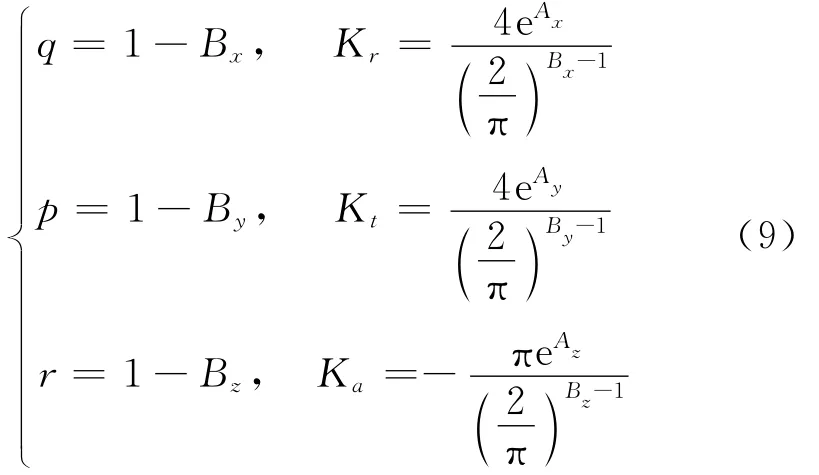
4）一般多项式切削力模型

计算获得X／Y／Z方向上的每齿平均铣削力为

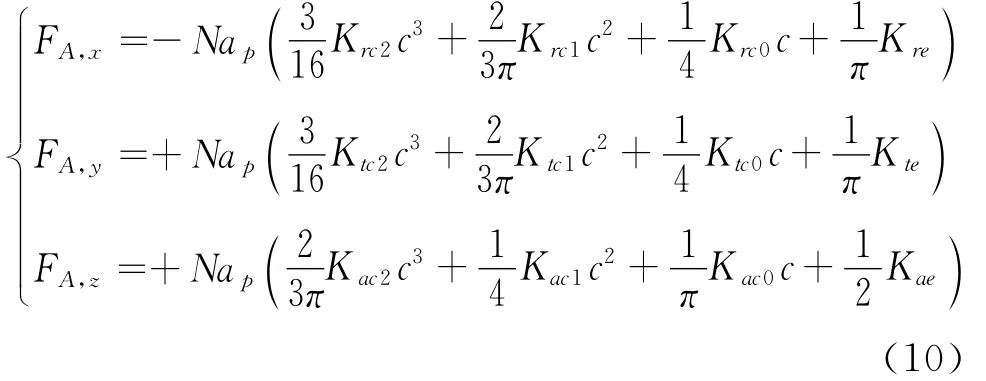
设已有m＋1组（m≥3）不同每齿进给量c（c0，c1，c2…cm）下的平均切削力数据，对X／Y／Z方向以｛c0c1c2c3｝为基函数分别进行最小二乘法曲线拟合。以X方向为例，由下方程组式可解得kx。

其中，

保持A不变，同理对X，Z方向进行辨识，可解出ky，kz向量：

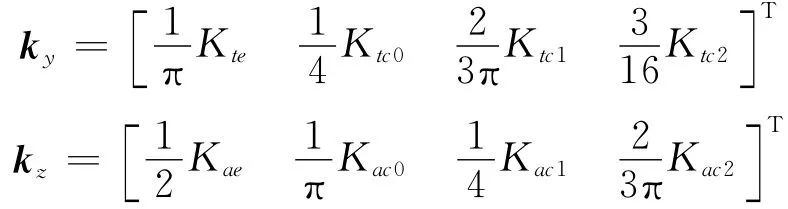
辨识后的切削力系数计算公式如下

2.2 辨识实验

结合切削实验，通过采集铣削过程中的X／Y／Z向切削力数据，对刀具／工件材料对的切削力系数进行辨识。实验采用槽铣的方式，与公式推导中的条件保持一致。为最大限度降低实验误差，总共采集9组实验数据，取主轴转速n＝4 000r／min保持不变，分别改变进给速度（F＝200，400，600mm／min）与切深（ap＝0.5，1，1.5mm）的取值。实验用机床为VMC0850B（如图2所示），切削用测力仪为Kistler 9257B。实验用刀具为KENNAMETAL圆柱螺旋立铣刀（ABDF1200A2AS），刀齿数为2，刀具直径为12mm。工件材料为铝合金7050。

图2 切削实验现场Fig.2 Experimental setup

分别应用2.1节的算法对上述四种切削力模型的系数进行辨识，结果如表2所示。

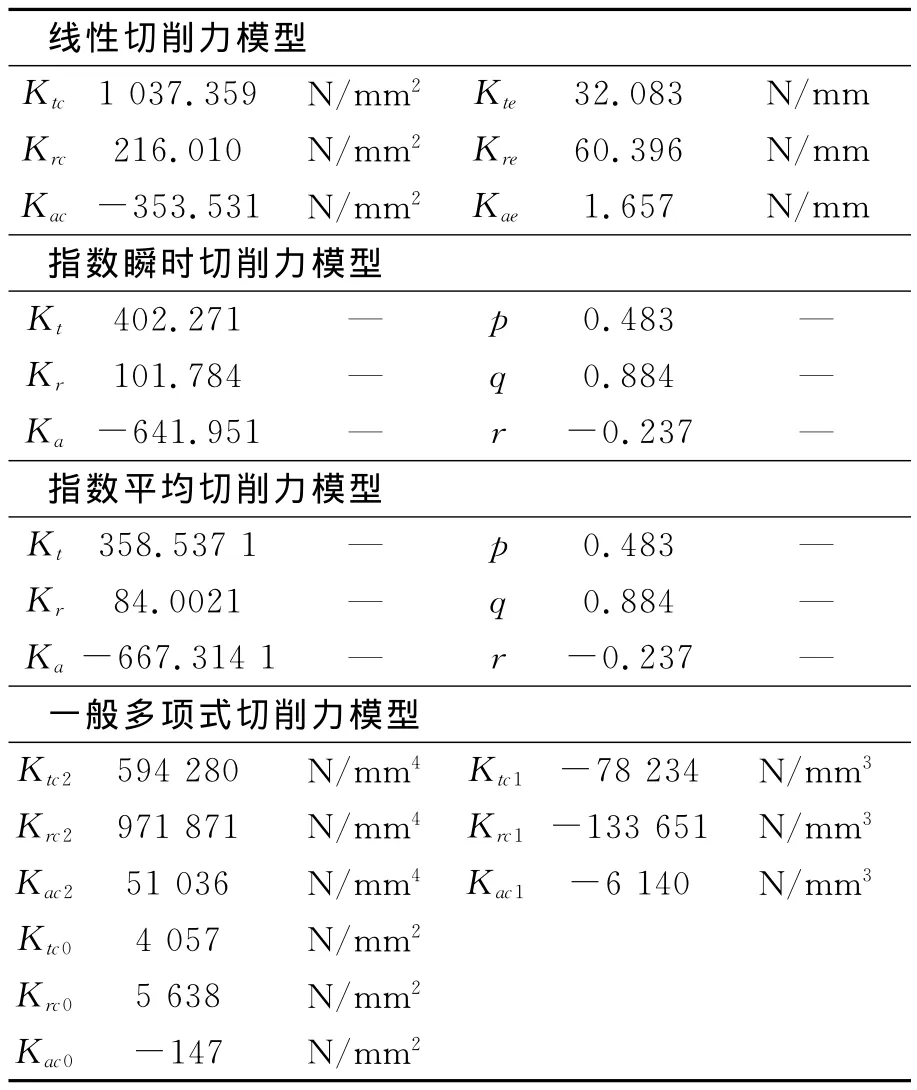
表2 辨识后的铝合金7050切削力系数Tab.2 Identified cutting force coefficients of Aluminum 7050

3 铣削力预测与实验对比

基于上述四种切削力模型及辨识后的切削力系数，通过式（2）预测X／Y／Z向铣削力并与实验结果进行对比（如图3，4所示）。由图可得，四种切削力模型的预测结果均与实验较吻合。通过计算每种模型预测值相对实验数据的平均误差，对模型的预测精度作进一步分析。以铝合金7050为例，由图5可得，线性、指数瞬时切削力模型的预测结果与实验数据最为接近（各向最大误差均小于8%），其次是一般多项式模型，指数平均模型的预测误差相对最大。与实验数据相比，线性、指数瞬时与一般多项式模型预测误差的最小值均在Y方向，误差值分别为0.25%，1.52%与1.58%；指数平均模型预测误差的最小值在Z方向，最小误差为5.05%。此外，由于螺旋立铣刀切削加工时的Z向铣削力数值较小，因而对线性、指数瞬时与一般多项式模型而言，X和Y方向的预测误差均比Z向误差大；但指数平均模型预测误差的最大值发生在Y方向，最大误差为16%。

4 铣削颤振稳定域仿真与对比

根据再生颤振理论，采用频域求解法预测各切削力模型下的颤振稳定域图，有关该方法的具体介绍可参考文献［1］。频域法求解的关键在于获取式（10）中的方向系数矩阵α。本文推导过程中，对指数瞬时、一般多项式模型中的高阶函数采用泰勒公式进行展开，详见附录。

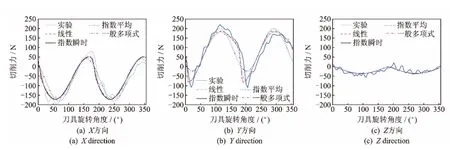
图3 四种切削力模型的三向铣削力仿真结果与实验对比。工件材料铝合金7050；刀具直径D＝12mm，刀齿数N＝2；切削参数：n＝4000r／min，F＝600mm／min，ap＝1.5mm，槽铣。Fig.3 Comparison of the simulated and experimental milling force in X／Y／Zdirections based on the proposed four cutting force models.Workpiece material：Aluminum 7050；tool diameter D＝12mm，teeth number N＝2；and cutting parameters：n＝4000r／min，F＝600mm／min，ap＝1.5mm，slot milling.

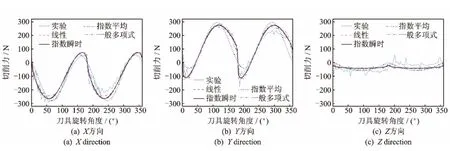
图4 四种切削力模型的三向铣削力仿真结果与实验对比。工件材料合金钢40Cr；刀具直径D＝16mm，刀齿数N＝2；切削参数：n＝3000r／min，F＝480mm／min，ap＝0.8mm，槽铣。Fig.4 Comparison of the simulated and experimental milling force in X／Y／Zdirections based on the proposed four cutting force models.Workpiece material：alloy steel 40Cr；tool diameter D＝16mm，teeth number N＝2；and cutting parameters：n＝3000r／min，F＝480mm／min，ap＝0.8mm，slot milling.

式中F（t）＝［FxFy］′，Δ（t）＝［ΔxΔy］′。

在获取切削力系数及方向系数矩阵α后，颤振稳定域图的预测还需要获取刀尖频响函数。以本文所使用的螺旋立铣刀为例（如图2所示），采用锤击实验进行测试。测试及分析软件为Cutpro V9.0，冲击力锤为PCB 086C03，加速度计为Kistler 8778A500，数据采集卡为NI 9233。测试获得刀尖沿机床坐标X／Y方向的频响函数如图6所示。

以工件材料铝合金7050为例，基于上述四种切削力模型所预测出的颤振稳定域如图7所示。由于基于线性切削力模型的铣削颤振稳定域频域求解方法的准确性已得到大量验证［1，2，9］，本文省略了重复针对该方法预测精度的实验验证工作，仅将另外三种切削力模型的预测结果与线性模型进行对比。

以图7（a）的半槽铣（c＝0.1mm）为例，线性切削力模型的极限切深值为5.6mm，指数瞬时与指数平均模型的预测值较接近，分别为4.2mm与4.0mm，一般多项式模型的预测值最小，为1.5mm。以图7（b）槽铣（c＝0.075mm）为例，线性与指数瞬时切削力模型的预测结果相近（极限切深值分别为1.9mm与1.7mm），而指数平均与一般多项式模型的预测极限值相对较低，均为1.2mm。综合以上分析，一般多项式模型的颤振稳定域预测精度与线性模型的差别最大，最大偏差超过50%。

此外，与线性切削力模型不同，由于指数瞬时、指数平均及一般多项式模型的方向系数矩阵α中包含了瞬时切削厚度h，因而可预测进给速度对颤振稳定域瓣的影响。限于文章篇幅，在本文中不予讨论。

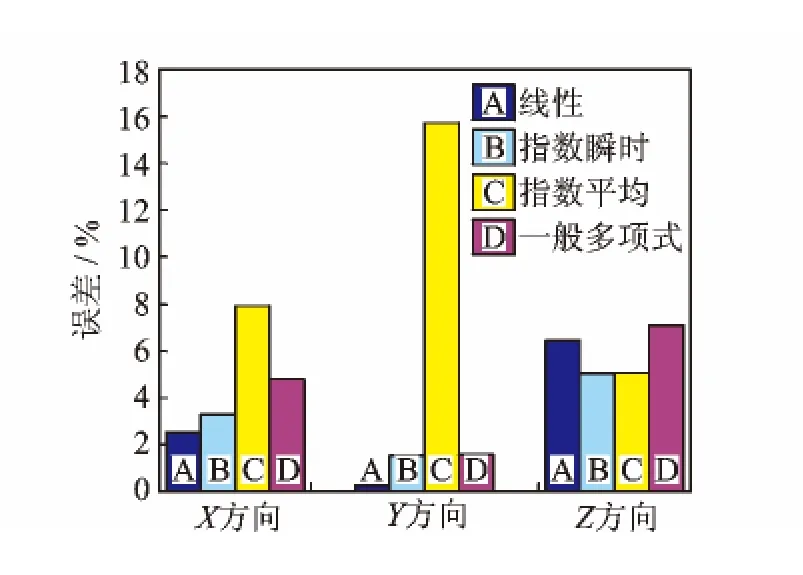
图5 四种切削力模型预测值相对实验数据的平均误差。工件材料铝合金7050；刀具直径D＝12mm，刀齿数N＝2；切削参数：n＝4 000r／min，F＝600mm／min，ap＝1.5mm，槽铣。Fig.5 Average error between simulated and experimental milling force based on the proposed four cutting force models.Workpiece material：Aluminum 7050；tool diameter D＝12mm，teeth number N＝2；and cutting parameters：n＝4 000r／min，F＝600mm／min，ap＝1.5mm，slot milling.

图6 刀尖位移频响函数Fig.6 Displacement frequency response function of the tool tip

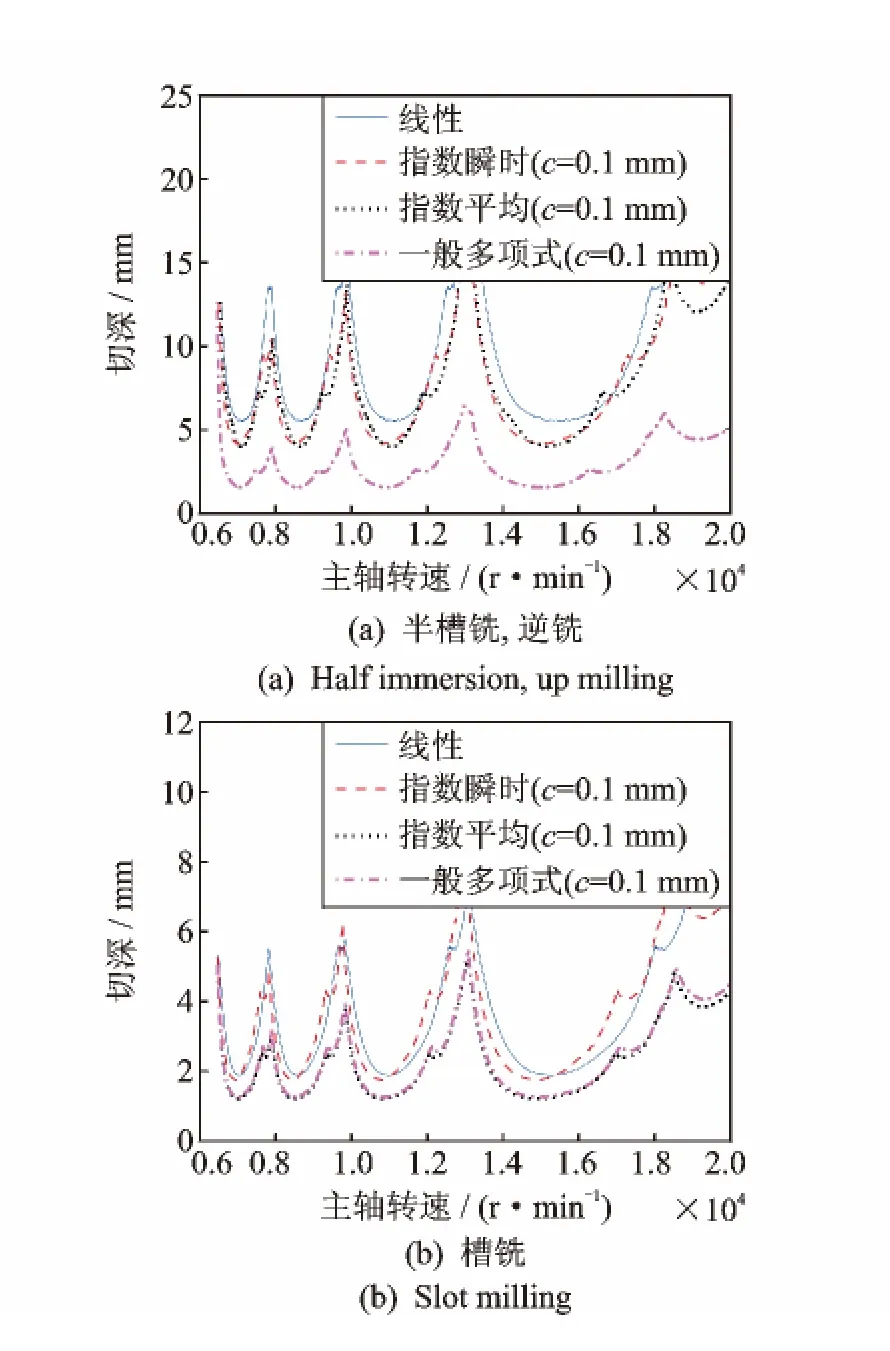
图7 基于四种切削力模型下的颤振稳定域图预测。工件材料铝合金7050；刀具直径D＝12mm，刀齿数N＝2Fig.7 Chatter stability prediction based on the proposed four cutting force models.Workpiece：Aluminum 7050；tool diameter D＝12mm，teeth number N＝2

5 结 论

（1）在铣削力预测部分，线性、指数瞬时切削力模型的预测结果与实验数据最为接近，其次是一般多项式模型，指数平均模型的预测误差相对最大，以铝合金7050为例，较实验值的最大平均误差为16%；

（2）在铣削颤振稳定域预测部分，线性、指数瞬时模型的预测值较为接近，其次是指数平均模型，一般多项式模型的预测值与线性模型的差别最大，最大偏差超过50%；

（3）综合铣削力与颤振稳定域预测结果，线性、指数瞬时切削力模型的预测精度高于指数平均与一般多项式模型。指数平均模型由于同时忽略了刃口力系数以及切屑厚度的瞬时变化，在部分情况下所预测的切削力幅值有可能保持恒定（如四齿铣刀、槽铣），与实验结果差距较大；

（4）相对线性模型，指数瞬时、指数平均及一般多项式模型均可预测进给速度对颤振稳定域的影响，缺点是在计算方向系数矩阵时，对以瞬时切削厚度为底数的幂函数采用了泰勒公式进行展开，忽略了高阶多项式，从而对稳定域瓣的预测结果造成一定影响。

［1］ ALTINTAS Y. Manufacturing Automation ［M］.Cambridge：Cambridge University Press（the Second Edition），2012.

［2］ 刘强，李忠群.数控铣削加工过程仿真与优化——建模、算法与工程应用［M］.北京：航空工业出版社，2011.LIU Qiang，LI Zhongqun.Simulation and Optimization of CNC Milling Process－Modeling，Algorithms and Applications［M］.Beijing：Aviation Industry Press，2011.

［3］ INSPERGER T，STEPAN G.Updated semi－discretization method for periodic delay－differential equations with discrete delay［J］.International Journal for Numerical Methods in Engineering，2004，61（1）：117—141.

［4］ DING Y，ZHU L M，ZHANG X J，et al.A full－discretization method for prediction of milling stability［J］.International Journal of Machine Tools and Manufacture，2010，50（5）：502—509.

［5］ BUDAK E.Mechanics and dynamics of milling thin walled structures［D］.The University of British Columbia，1994.

［6］ FAASSEN R P H，WOUW N V D，OOSTERLING J A J，et al.Prediction of regenerative chatter by modelling and analysis of high－speed milling［J］.International Journal of Machine Tools and Manufacture，2003，43（14）：1 437—1 446.

［7］ 张臣，周儒荣，庄海军，等.基于Z－map模型的球头铣刀铣削力建模与仿真［J］.航空学报，2006，27（2）：347—352.ZHANG Chen，ZHOU Rurong，ZHUANG Haijun，et al.Modeling and simulation of ball－end milling forces based on Z－map Model［J］.Acta Aeronautica et Astronautica Sinica，2006，27（2）：347—352.

［8］ WAN M，ZHANG W H，DANG J W.A Novel cutting force modeling method for cylindrical end mill［J］.Applied Mathematical Modelling，2010，34（3）：823—836.

［9］ JENSEN S A，SHIN Y C.Stability analysis in face milling operations，part 2：experimental validation and influencing factors［J］.Journal of Manufacturing Science and Engineering，1999，121（4）：606—614.

［10］MUNOA J，ZATARAIN M，BEDIAGA I，et al.Stability study of the milling process using an exponential force model in frequency domain［A］.CIRP －2nd International HPC Conference［C］.Vancouver，2006.

［11］尹力，刘强.基于偏最小二乘回归（PLSR）方法的铣削力模型系数辨识研究［J］.机械科学与技术，2005，24（3）：269—272.YIN Li，LIU Qiang.Study on the identification of the milling force parameter model based on partial least square regression and application［J］.Mechanical Science and Technology，2005，24（3）：269—272.

［12］梁睿君，叶文华，黄翔.铣削加工3维稳定性预测［J］.四川大学学报（工程科学版），2011，43（3）：219—224.LIANG Ruijun，YE Wenhua，HUANG Xiang.Threedimensional stability predication for milling processes［J］.Journal of Sichuan University （Engineering Science Edition），2011，43（3）：219—224.