飞机起落架缓冲器参数可靠性灵敏度分析

张 峰，杨旭锋，刘永寿，南 华，2

（1.西北工业大学力学与土木建筑学院飞行器可靠性工程研究所，陕西 西安710129；2.兰州万里航空机电有限责任公司，甘肃 兰州730700））

引 言

缓冲系统是飞机起落架的重要组成部分。飞机在着陆过程中受到很大的冲击载荷，这要求缓冲系统能消耗掉飞机着陆冲击带来的能量。缓冲系统性能的好坏直接影响到飞机着陆过程的安全性，其故障轻者导致飞机受损，重者酿成机毁人亡的惨剧。因此，缓冲系统的设计技术在起落架设计中占有重要的地位。缓冲器是缓冲系统中重要的组成部件，其参数配置的恰当与否，对缓冲系统性能有着决定性的影响［1，2］。

目前，起落架缓冲系统的设计仍基于安全系数法的设计理念［3～6］。文献［4］建立了前起落架单腔定油孔和单腔变油孔的虚拟样机、主起落架单腔定油孔和双腔定油孔的虚拟样机，分别开展在使用功和最大功情况下的落震仿真分析。文献［5］建立某型飞机主起落架缓冲器的虚拟样机模型，采用基于正交试验设计的响应面方法获得优化参数和优化目标间的数学关系，并通过优化来提高多支柱起落架的着陆缓冲性能。文献［6］借助 MSC.ADAMS软件建立了起落架缓冲系统多体运动学仿真模型，研究缓冲系统充填参数对着陆性能的影响。

需要指出的是，这些研究忽略了缓冲器在设计、制造过程参数的随机不确定性［7］。研究表明，缓冲器一些关键设计参数的微小波动会导致缓冲系统性能有很大的变化。可靠性灵敏度采用失效概率对基本变量分布参数的偏导数来度量，得到的灵敏度序列能快速识别出影响系统可靠性的关键参数，对系统改设计提供指导［8，9］。因此，本文开展起落架缓冲器参数的灵敏度分析。首先采用MSC.ADAMS软件建立起落架系统落震仿真模型，通过多体动力学分析对缓冲系统的效率、缓冲器的行程以及起落架最大过载等指标进行考核；考虑设计、制造、操作以及环境因素带来的影响，将缓冲器的初始充填压力、初始充气体积、压气面积、活塞杆面积、气体多变指数、压油面积、主油孔面积、主油液流量系数和油液密度等参数处理为随机变量，并以缓冲系统的效率、缓冲器的行程以及起落架最大过载等指标建立多模式下缓冲器参数的灵敏度分析模型，采用基于Kriging方法的代理模型建立缓冲器输出响应与设计参数的函数关系，再采用重要抽样法求解缓冲器参数的灵敏度。

1 缓冲器参数灵敏度分析模型

1.1 起落架系统落震仿真分析

某型飞机摇臂式起落架采用的是油气式缓冲器，其结构模型如图1所示。

在MSC.ADAMS软件中建立起落架系统落震仿真模型如图2所示，通过多体动力学理论来分析缓冲系统着陆过程中的性能。

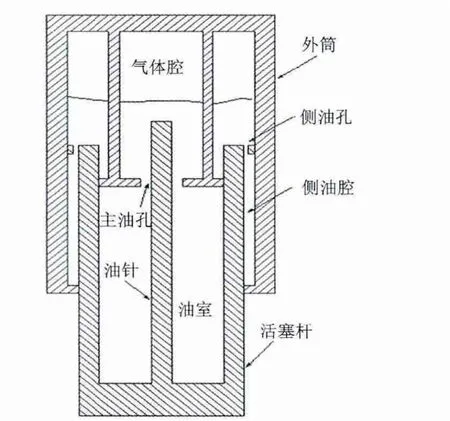
图1 起落架缓冲器结构模型Fig.1 Shock absorber model of a landing gear system

图2 某型飞机起落架系统落震仿真模型Fig.2 The drop simulation model of an aircraft landing gear system

通过起落架系统落震仿真分析得到缓冲器行程为294.7mm，缓冲系统的效率为79.97%。起落架轮胎所受地面冲击载荷变化曲线如图3所示，所受地面最大载荷为340.7kN，着陆过载为1.66。缓冲系统的效率η、缓冲器的行程Stroke以及起落架最大过载max（Force）等指标均满足设计要求。

图3 起落架所受冲击载荷的变化曲线Fig.3 The change curve of the landing gear impact load

1.2 缓冲器参数灵敏度分析模型

由于设计、制造、操作以及环境因素带来的影响，导致缓冲器的初始充填压力、初始充气体积、压气面积、活塞杆面积、气体多变指数、压油面积、主油孔面积、主油液流量系数和油液密度等参数为随机变量。当随机变量之间具有相关性时，需要预先通过Nataf变换将相关变量转化为相互独立的随机变量［10］。

缓冲器参数的分布类型及其均值、变异系数、标准差如表1所示，参数的变异系数通过查阅相关手册或凭工程经验获得［2］。

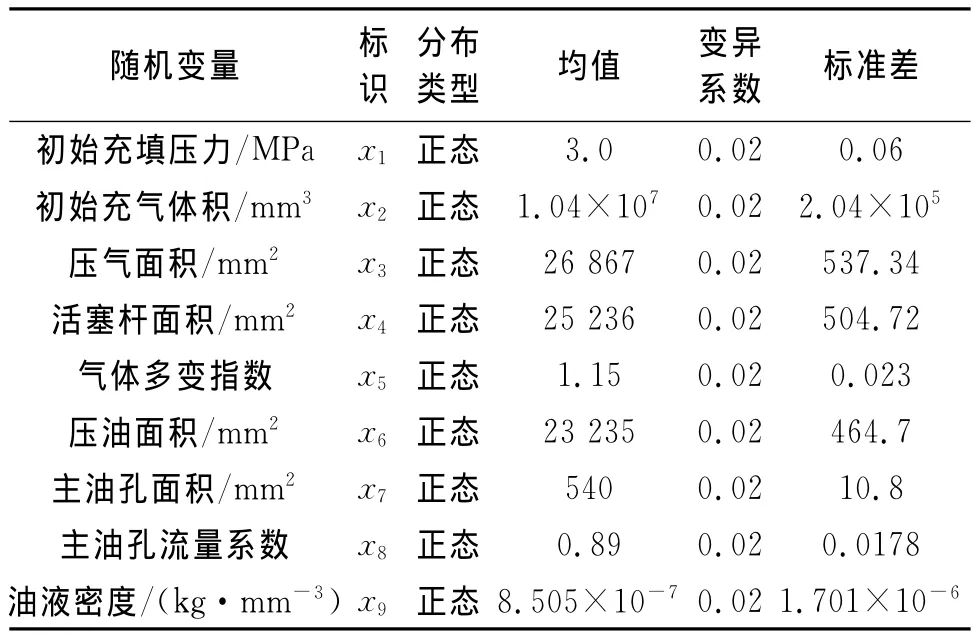
表1 随机变量的分布类型及参数Tab.1 Distribution type and parameters of random variables

假定随机变量xk（k＝1，2，…，9）的概率密度函数为fk（xk），向量x＝（x1，x2，…，x9），则系统不确定性变量的联合概率密度

考核缓冲器结构设计是否合理，重在于考核缓冲系统的效率、缓冲器的行程以及起落架的最大过载等三个指标。由于（x1，x2，…，x9）均为随机变量，导致η，Stroke和 max（Force）均为随机变量，是向量x的隐函数，需要借助MSC.ADAMS软件进行起落架系统落震仿真分析来获得。

在评估缓冲系统功能可靠性时，采用系统的效率η（x）、缓冲器的行程Stroke（x）以及起落架的最大过载max（Force（x））等三个指标分别建立相应的功能函数。

（1）效率失效：该缓冲器作为起落架系统主要吸收能量的装置，其效率η（x）不能低于预定值η＊，由此定义功能函数g1（x）如下式

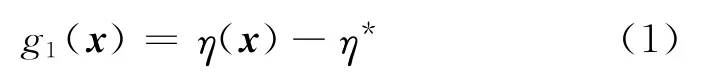
（2）行程失效：该缓冲器的使用行程Stroke（x）不得大于0.9倍的最大行程S＊，由此定义功能函数g2（x）如下式

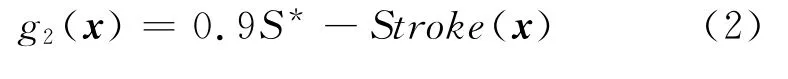
（3）过载失效：该起落架着陆载荷实际值的最大值max（Force（x））不能大于最大着陆载荷容许值F＊，由此定义功能函数g3（x）如下式

三个指标中的任一一个不满足设计要求，都会影响缓冲系统的功能，所以这三个指标为串联关系。定义缓冲系统功能可靠性的功能函数为G（x），G（x）可表示为

缓冲系统的失效概率Pf用下式来计算

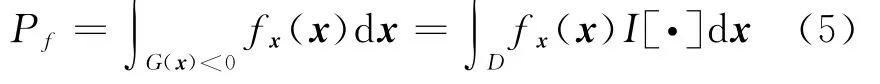
式中D为整个变量空间，I［·］为指示函数，满足。

根据文献［8，9］，定义缓冲器参数的可靠性灵敏度为失效概率对基本变量分布参数的偏导数。式（5）对第k个变量xk的分布参数θk（θk为μk或σk）求导数，得到可靠性灵敏度如下式所示

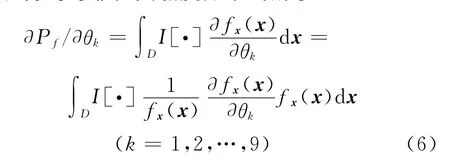
式（6）中，当θk＝μk时，∂fx（x）／∂θk可写为

当θk＝σk时，∂fx（x）／∂θk可写为

2 缓冲器参数可靠性灵敏度分析

在缓冲器参数可靠性灵敏度分析中，存在两个难题。

（1）由于缓冲器的复杂性，缓冲系统的效率η（x）、缓冲器的行程Stroke（x）、着陆载荷实际值的最大值max（Force（x））等指标均是x的隐函数，需要借助MSC.ADAMS软件进行起落架系统落震仿真分析才能得到响应值。可靠性灵敏度分析多次调用MSC.ADAMS仿真软件进行功能函数的计算，这需要很大的计算量。因此，缓冲器参数的可靠性灵敏度分析需要借助高精度的代理模型对功能函数进行拟合［11］。Kriging方法从变量相关性和变异性出发，在有限区域内对区域化变量的取值并进行无偏和最优估计，具有很高的拟合精度［12，13］。因此，本文采用Kriging代理模型来拟合缓冲系统的三个功能函数gi（x）（i＝1，2，3）。

（2）缓冲系统的功能涉及到η（x），Stroke（x），max（Force（x））三个指标，其参数的可靠性灵敏度是一个多模式耦合问题。在多模式的参数可靠性灵敏度分析中，一次二阶矩方法适合于解决线性极限状态方程这类问题，对缓冲器这类复杂系统进行可靠性灵敏度分析估算误差较大。Monte Carlo法是对变量的个数、变量的概率分布及极限状态的形式等均无限制，但该方法收敛缓慢、计算量巨大。重要抽样法采用重要抽样函数进行抽样，能使更多的样本点落入失效域，从而提高抽样效率，减少计算量［14，15］。传统重要抽样法需要预先计算极限状态方程的设计点，而多极限状态方程的设计点难以求解。构建重要抽样函数的另一种思路是保持抽样中心在均值点不变，将标准差扩大λ倍来构建重要抽样函数，该策略不需要求解极限状态方程的设计点，也不受极限状态方程的个数限制［16］。因此本文通过该方式构建重要抽样函数来求解缓冲器参数的可靠性灵敏度。

2.1 功能函数基于Kriging模型的拟合

在Kriging代理模型中，首先需要产生插值试验点。拉丁超立方抽样设计（LHS）方法能在预定的抽样空间抽出较为均匀的实验点［17］，因此本文采用LHS方法产生m个试验样本，记为Xt＝（Xt1，Xt2，…，Xt9）（t＝1，2，…，m），对应的功能函数值为gi（Xt）（t＝1，2，…，m；i＝1，2，3）。利用功能函数值和试验点建立Kriging的近似模型，如下式所示

式中C＝ ［c1（X），c2（X），…，c9（X）］，α＝ ［α1，α2，…，α9］T，ck（X）（k＝1，2，…，9）是预先给定的多项式函数，αk为回归模型的待定系数，Z（X）是一均值为0、方差为σ2的高斯过程，其协方差如下式所示

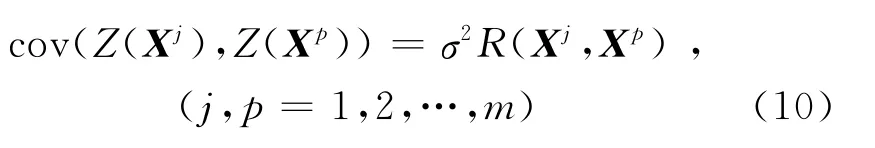
式中R为试验点Xj和Xp的相关函数，它与试验点之间在空间的位置密切相关。R选取Gaussian函数形式，如下式所示

式中d表征了试验点Xj、Xp之间的距离，如下式

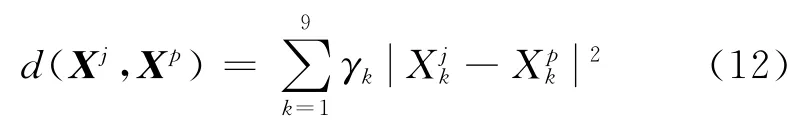
当j＝p时，

从式（13）可以看出，R（Xj，Xp）构成的对角元为1。R是m×m的相关系数阵，形式如下式

假设采用重要抽样法获得的样本为x，通过式（9）得到基于Kriging模型样本x的预测响应值~gi（x），如下式

式中Gi＝［gi（X1），gi（X2），…，gi（Xm）］，r（x）为预测点x与m个插值点之间的相关系数构成的列向量，如下式

x的回归模型系数α采用最小二乘法来求解，其估计式为

对式（9）中Z（X）的方差进行估计，估计值如下式

在式（18）中，R满足下式

采用极大似然算法求解γi即可建立式（9）所示的Kriging代理模型。

在本文中，通过LHS方法产生500个试验点，随机抽取400个试验点建立缓冲系统三个功能函数g1（x），g2（x），g3（x）基于 Kriging方法的代理模型，将余下的100个试验点进行模型的预测精度测试，各响应的均方根误差（RMSE）和最大相对误差（MRE）均小于3%，满足工程要求。

2.2 基于重要抽样法的可靠性参数灵敏度分析

对于式（6）所示的可靠性灵敏度，引入重要抽样函数h（λ，x）（λ＞1），则参数的可靠性灵敏度改写为下式

推导式（20）基于重要抽样法的无偏估计∂＾Pf／∂θk及其方差Var（∂＾Pf／∂θk）、变异 系数CV（∂＾Pf／∂θk）如下式所示

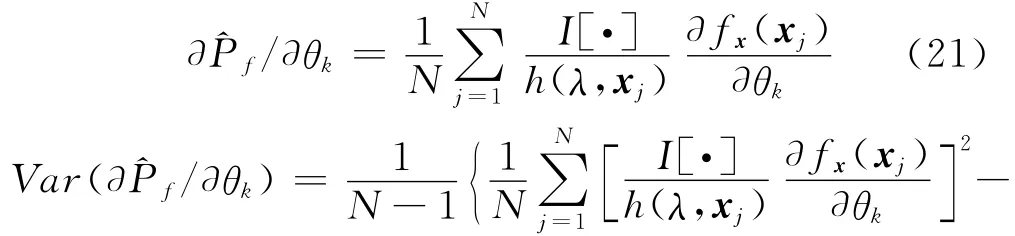
式中xj为重要抽样函数h（λ，x）抽取的第j个子样，N为样本总数目。

在本文中，变量xk（k＝1，2，…，9）是服从N（μk，σ2k）正态分布，重要抽样函数h（λ，x）可表示为下式

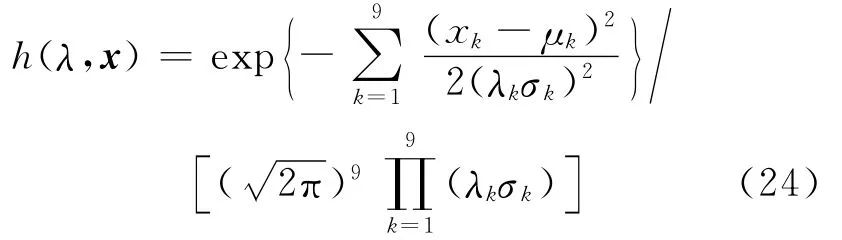
3 参数可靠性灵敏度结果分析

在缓冲器参数可靠性灵敏度分析中，需要对灵敏度结果进行无量纲的归一化处理，如下式所示

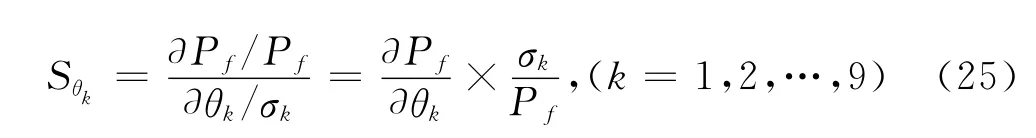
基于Kriging模型和重要抽样法的缓冲器参数可靠性灵敏度分析结果如图4所示。

图4 缓冲器参数的可靠性灵敏度Fig.4 Reliability sensitivities of shock absorber parameters

从图4可以看出，压气面积、压油面积、主油孔面积、主油孔流量系数的均值和标准差对起落架缓冲系统的可靠性影响都非常大，在缓冲器改设计中要重点关注这些参数。

4 结 论

（1）在多体动力学仿真的基础上，建立了起落架缓冲器参数的可靠性灵敏度分析模型；

（2）针对缓冲器参数可靠性灵敏度分析中的多模式及隐式功能函数问题，给出了该问题基于Kriging代理模型和重要抽样法的求解过程；

（3）通过参数可靠性灵敏度分析，确定压气面积、压油面积、主油孔面积、主油孔流量等参数为关键参数，为缓冲器改设计提供指导。

［1］ 航空航天工业部科学技术委员会.飞机起落架强度设计指南［M］.成都：四川科学技术出版社，1989.Science and technology committee of aeronautics and astronautics.Introduction to design for airplane landing gear［M］.Chengdu：Sichuan Science and Technology Press，1989.

［2］ 《飞机设计手册》总编委员会.飞机设计手册（第14册）［M］.北京：航空工业出版社，2003.Aircraft design handbook general editorial board.Aircraft Design Handbook （Volume 14）［M］.Beijing：Aviation Industry Press，2003.

［3］ Zdravko T，Milan V，Hinko W.Numerical simulation of landing aircraft dynamics［J］.Strojarstvo，2009，51（6）：657—665.

［4］ 张璞，刘向尧，聂宏，等.民用飞机起落架缓冲器选型与对比分析研究［J］.航空工程进展，2011，2（3）：287—291.Zhang P，Liu XY，Nie H，et al.Research on types and comparisons of landing gears shock absorber for civil airplane［J］.Advances in Aeronautical Science and Engineering，2011，2（3）：287—291.

［5］ 刘小川，马晓利，孙侠生，等.基于响应面方法的多支柱起落架着陆缓冲性能优化［J］.振动工程学报，2010，23（3）：305—309.Liu X C，Ma X L，Sun X S，et al.Performance optimization of shock absorber for multi－strut landing gear based on RSM［J］.Journal of Vibration Engineering，2010，23（3）：305—309.

［6］ 侯赤，万小朋，赵美英.虚拟样机技术在飞机地面载荷分析中的应用［J］.哈尔滨工业大学学报，2009，41（11）：134—137.Hou C，Wan X P，Zhao M Y.Application of virtual prototyping technology in the analysis of aircraft ground load［J］.Journal of Harbin Institute of Technology，2009，41（11）：134—137.

［7］ 赵世春，喻天翔，王慧，等.仿真技术在飞机起落架可靠性分析中的应用研究［J］.航空工程进展，2011，2（4）：444—448.Zhao S C，Yu T X，Wang H.Application of simulation technology on reliability analysis for aircraft landing gear system［J］.Advances in Aeronautical Science and Engineering，2011，2（4）：444—448.

［8］ Wu Y T.Computational methods for efficient structural reliability and reliability sensitivity analysis［J］.AIAA J，1994：32（8）：1 717—1 723.

［9］ Wu Y T，Sitakanta M.Variable screening and ranking using sampling－based sensitivity measures［J］.Reliability Engineering and System Safety，2006，91（6）：634—647.

［10］Li H S，Lu Z Z，Yuan X K.Nataf transformation based point estimate method［J］.Chinese Science Bulletin，2008，53（17）：2 586—2 592.

［11］张崎，李兴斯.基于Kriging模型的结构可靠性分析［J］.计算力学学报，2006，23（2）：176—179.Zhang Q，Li X S.Analysis of structural reliability based on Kriging model［J］.Chinese Journal of Computational Mechanics，2006，23（2）：176—179.

［12］Echard B，Gayton N，Lemaire M.AK－MCS：An active learning reliability method combining Kriging and Monte Carlo Simulation［J］.Structural Safety，2011，33：145—154.

［13］Vincent D，Bruno S，Bourinet J M.Reliability－based design optimization using Kriging surrogates and subset simulation［J］.Struct.Multidisc Optim，2011，44：673—690.

［14］Melchers R E.Search－based importance sampling［J］.Structure Safety，1990（9）：117—128.

［15］吕震宙，岳珠峰.多个模式联合失效的设计点及概率的计算［J］.计算力学学报，1998，15（4）：442—447.Lu Z Z，Yue Z F，Joint design point and failure probability calculations of multi－mode［J］.Chinese Journal of Computational Mechanics，1998，15（4）：442—447.

［16］吴斌，欧进萍，张纪刚.结构动力可靠度的重要抽样法［J］.计算力学学报，2001，18（4）：478—482.Wu B，Ou J P，Zhang J G.Importance sampling techniques in dynamical structural reliability［J］.Chinese Journal of Computational Mechanics，2001，18（4）：478—482.

［17］Helton J C，Davis F J.Latin hypercube sampling and the propagation of uncertainty in analysis of complex systems［J］.Reliability Engineering and System Safety，2003，81（1）：23—69.