基于迭代凸优化的恒模波形合成方法

李秀友 薛永华 董云龙 关 键

1 引言

认知雷达是未来雷达发展的主要方向之一，认知雷达由于引入了闭环反馈结构，可以根据获取的场景信息自适应调整发射波形，从而改善系统性能[1]。波形设计是认知雷达关键技术之一，波形优化设计是在一定的约束条件下最大化准则函数，准则函数的选取取决于雷达系统的任务和工作模式[26]-。

大量文献研究了认知雷达的波形优化问题。文献[7]首先提出了利用目标和回波的最大互信息设计发射波形，从信息论角度解决波形优化问题。文献[8]研究了基于距离扩展目标最大输出信杂噪比的波形设计方法，设计得到最优发射波形和接收滤波器的功率谱。文献[9]分析了广义平稳高斯杂波中点目标的检测问题，将回波信号统一变换到频域，再根据对数似然比检测器的最大检测概率准则，用“注水法”求得最优发射波形能量谱。

以上最优波形设计算法只能得出优化波形的能量谱，要应用于实际雷达系统还需要合成时域波形，为了提高发射机功率利用率，常需要合成满足能量谱约束的恒模波形。目前基于波形能量谱合成时域信号常用的有3种方法，分别是Durbin 法、驻留相位法[10]和迭代合成法[11]。Durbin法相对简单，但不能满足恒模要求，驻留相位法合成波形具有恒模特性，但是无法很好地拟合复杂形状能量谱，迭代算法收敛速度慢，能量谱边沿拟合误差大。

满足给定能量谱的恒模波形设计问题需要同时在频域满足给定频谱，在时域满足恒模要求[11]。这类约束在两个不同集合中的优化问题常采用交替投影法，这种处理方法广泛应用于约束条件下的波束形成和时域波形合成中[1214]-。此类问题求解通常采用迭代方法在两个不同集合之间交替投影，逐步逼近满足约束条件的解，该解存在于两个集合的交集中[15]。以上迭代方法在不同集合中以各自约束条件为目标函数进行优化处理，而不考虑相互之间的影响，这种处理方法往往会导致整体收敛速度变慢，收敛到性能较差的局部最优值[16]。文献[17]在设计满足峰均功率比（Peak-to-Average Power Radio,PAPR）约束的正交频分复用（OFDM）信号时，将信号频域失真和时域PAPR约束联合优化，使得每步优化过程能够同时兼顾两个约束条件，提高了收敛速度，降低了误码率。

受上述思路的启发，本文在文献[11]迭代波形合成算法的基础上，将频谱逼近过程构造成约束条件下的优化问题，其中时域恒模特性作为约束条件，波形能量谱与期望能量谱的误差作为目标函数。在优化处理过程中将恒模约束放松为PAPR约束，并对频谱进行加权处理，进一步降低阻带内功率水平，然后通过一系列变换操作将优化问题转化成二阶锥规划（Second-Order Cone Programming, SOCP）问题求解，最后通过仿真结果验证算法的有效性。

2 经典时域波形合成算法

给定期望的N点幅度谱密度函数s（k）, 0k= ,1,,1N-…，需要设计M点单位幅值恒模复信号：如果M＜N，则x（n）补零到N点，使得x（n）的N点DFT变换y（k）接近期望的幅度谱s（k）。

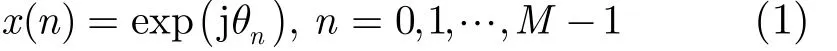
为使得设计的恒模信号幅度谱接近期望值，设y（k）的相位为φ（k），则最小二乘误差可写为

定义 s =

s（ 0）ejφ（0）,s （ 1）ejφ（1）,… ,s （ N - 1）e，并定义 x =[x （ 0）,x （ 1）,… ,x （ N - 1）]T，则式（2）经过一系列变换可以得到x的最小二乘估计值，并将时域信号估计值x做幅度归一化处理，即得到恒模的时域信号。

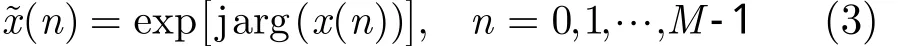
其中arg（）⋅表示取相位，文献[11]将上述两步估计构成迭代算法，将第i次迭代的幅度谱相位估计值（）（）ik φ 直接赋给期望幅度谱，即

图 1 基于频谱最小二乘误差的恒模波形合成法

上述算法在频谱逼近处理过程中，直接将期望幅度谱s（k）作为下一次迭代的频谱幅值，没有考虑到做IFFT之后时域信号的峰值大小。时域不做约束的频谱逼近处理将会导致时域信号出现较大的峰值，需要多次迭代才能得到满足恒模和幅度谱逼近的波形，降低了收敛速度。该算法将设计波形幅度谱和期望幅度谱的整体误差作为代价函数，没有重点考虑阻带内频谱误差对性能的影响。而波形阻带部分通常是强杂波或强干扰所在频段，需要设计较深的凹口来提高信杂比或信干比。

3 加权迭代优化波形合成算法

本文提出的算法是在文献[11]迭代算法（下文简称Kay算法）的基础上，针对频谱逼近过程存在的不足进行改进。首先，构造波形时域PAPR约束条件下的优化表示式，同时兼顾幅度谱逼近程度和时域起伏大小；然后对频谱矢量加权处理，抑制阻带内发射功率水平；最后将优化问题转换成二阶锥规划（SOCP）问题，利用内点法求解。

3.1 建立满足约束条件的目标函数

此处定义时域信号PAPR：

其中 ⋅2表示2-范数，⋅∞表示无穷范数。定义1维加权矢量w=[w（0）,w（1）,…,w（N-1）]T，引入频谱加权误差矢量值（Weighted Error Vector Magnitude,WEVM）用于表征两个频谱矢量加权误差大小，表达式为其中，运算符号‘·’表示对应元素乘积。

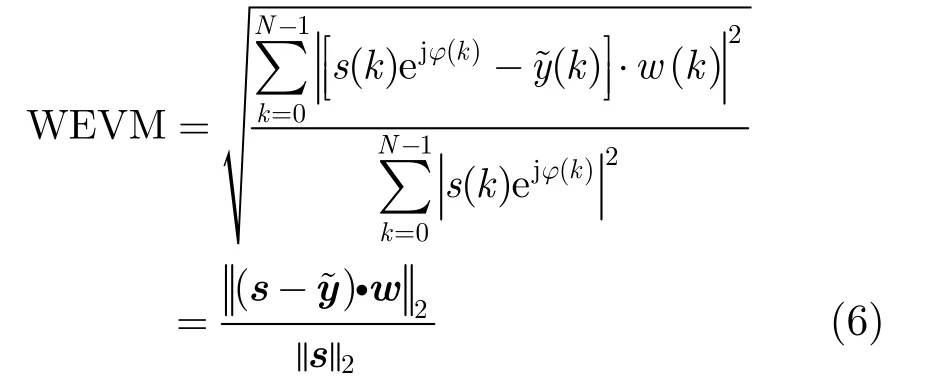
上述迭代波形合成算法中直接将期望幅度谱s（k）作为下一次迭代输入信号频谱的幅值，这会导致合成信号的幅值出现大的波动，使得迭代收敛速度变慢，且每步迭代过程没有最优准则保证。本文提出了在PAPR约束下的加权误差矢量值（WEVM）最小化算法：

由于约束函数式（7d）为非凸的，优化模型式（7）也是非凸的，这使得其数值求解比较困难。

3.2 基于SOCP的波形优化设计

为将优化问题式（7）修正成凸的表达式，用xi-122近似替换xi22，则非凸约束式（7d）可以变换成[17]

由于在第i次迭代过程中xi-122是已知的，PAPRMax为预先设置的参数，则每次迭代过程中约束峰值Ti可以计算求得，因而非凸约束转化成凸约束式（8）。其中，当PAPRMax值足够大时，约束条件式（7d）失效，优化算法退化为文献[11]最小二乘估计算法。优化模型式（7）可以简化为

其中，矩阵A由N维IFFT旋转因子矩阵的前M行构成，式（9）可以进一步表示成二阶锥规划（SOCP）[18,19]

3.3 加权优化迭代波形合成算法

加权优化迭代波形合成算法流程如图2所示，主要包括PAPR约束下的最优幅度谱加权逼近处理和信号幅度恒模处理过程。定义相邻两次迭代过程时域波形变化量。

图 2 加权优化迭代波形合成流程图

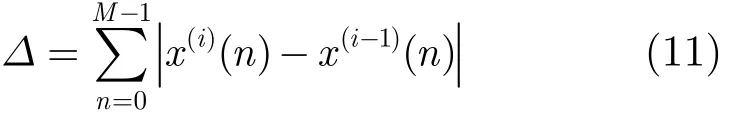
其中x（i）（n） 表示第i次迭代时域估计值。具体迭代步骤如下，其中步骤1用于初始化，步骤2至步骤7循环迭代直至终止。

步骤 1 初始化过程，设定峰均功率比PAPRMax和加权系数矢量w；

步骤 2 如果i=1，则令 x（0）（n ） = exp（jθn（0）） ，其中 k =0,1,… ,M -1,θn（0）为随机产生的相位，服从[- π, π]上 的 均 匀 分 布 ， 当i≠1时 ， 令x~（i）（n）=x~（i-1）（n），利用FFT将 x~i变换到N点离散频域形式yi=[y（i）（0）,y（i）（1）,… ,y（i）（N-1）]；

步骤 3 执行约束条件下的加权优化算法式（10），得到最优逼近滤波器hi，并令 y~i=yi. hi；

步骤 4 根据 y~i值自适应调整加权系数 wi-1，控制阻带整体功率水平或峰值频点功率；

步骤 5 利用IFFT将 y~i变换到时域信号xi；

步骤 6 利用式（3）对信号xi幅值做归一化处理，得到恒模的时域信号 x~i；

步骤 7 当 Δ ＜ 0 .01 × M 时，循环终止，否则返回步骤2。

3.4 算法复杂度分析

SOCP模型可以用标准内点法求解，优化模型最差情况下的运算量为O（N3）[18]，每次迭代过程中，包含一次FFT和IFFT运算，运算量为O（Nlog2（N）），阻带内峰值搜索及信号归一化处理运算量为O（N）。当最大迭代次数为P时，所提算法整个运算量为O（PN3+PNlog2（N）+PN）。

4 仿真结果及性能分析

下文通过计算机仿真验证本文算法的有效性和优越性。为便于比较分析，本文仿真设计与文献[11]相同能量谱密度的最优雷达发射波形，表示式为

其中， Pn（f）为噪声功率谱密度， Ph（f） 为杂波功率谱密度，λ为由能量约束决定的常数。仿真中最优能量谱密度设为100个频点，对应的能量谱如图3所示。从图中可以看出，在部分频点上信号能量谱较大，以下简称为通带频段，在其余频点上能量为零，为强干扰区或杂波区，简称阻带频段。希望设计的波形在恒模约束下与最优波形的能量谱最接近，其中过渡频带的拟合程度最能反应波形的逼近性能，阻带凹口深度决定了所设计波形对强杂波及干扰的抑制能力。

因此，以下仿真分析将从算法收敛速度，阻带内整体能量大小，峰值功率水平以及过渡频段的频谱拟合程度等方面综合分析算法的性能。

4.1 固定权系数抑制阻带能量

为了分析权系数w=[w（0）,w（1）,…,w（N-1）]T对阻带凹口的影响，令阻带内对应频点上的权重为10 dB，通带内对应频点权系数为0 dB，权系数表示为

其中固定权系数在每次迭代过程中保持不变，权系数的设定在4.3节中说明。图4（a）给出了本文固定权系数优化算法与Kay算法的能量谱，当迭代次数P=200时，在阻带内大部分频点上，本文优化算法功率低于Kay算法，图4（b）给出了50次仿真能量谱的平均值，阻带内各频点上本文优化算法低于Kay算法。图5给出了两种算法阻带内积分能量随迭代次数变化曲线，本文算法比Kay算法阻带内能量下降快且低5.3 dB；分析10次和50次仿真结果平均值可以看出不同初始相位对收敛结果略微有影响，但是不会改变算法的整体收敛性；由于迭代过程中对时域波形的恒模处理，收敛曲线局部无法保证单调下降，大量仿真实验表明，局部非单调不影响整体收敛趋势。图6给出了不同波形长度两种算法累积能量谱密度，本文算法跟期望累积能量谱密度曲线比较接近，在边缘区域也比Kay算法更接近理想曲线。其中累积能量谱密度定义为

根据式（11）的收敛条件，当波形长度M=20, 50和100时，收敛所需的迭代次数分别为7次，8次和10次。可以看出本文算法和Kay算法的累积能量谱密度均随着波形长度M的增加而逼近理想值，且在不同M值时，本文算法优于Kay算法。

4.2 自适应调整权系数抑制阻带内峰值频点

固定权系数无法控制阻带内频点的峰值能量，为了降低整个阻带频点上的能量，在每次迭代过程中，搜索阻带内频谱峰值点，将该对应点的权系数增大到20 dB，其余点权系数不变，如式（15）所示。通过优化设计降低该频点的能量，经过反复迭代，阻带内所有频率点的能量得到有效控制。图7给出了两种算法在相同初始相位时，经过200次迭代所得恒模波形的能量谱，本文优化迭代算法阻带内最大峰值功率降为0.4 dB，比通带低21.6 dB，比Kay算法阻带内峰值功率6.8 dB低6.4 dB。图8给出了阻带内能量随着迭代次数收敛情况，该算法能有效收敛，且本文算法比Kay算法阻带能量低5.8 dB，同时给出了10次和50次仿真结果平均值，可以看出不同初始相位对收敛过程有一定影响，但是不会改变算法的收敛趋势。迭代循环终止准则按照式（11），则不同信号长度M的收敛次数跟固定权系数算法相近。

4.3 权系数设定及运算量分析

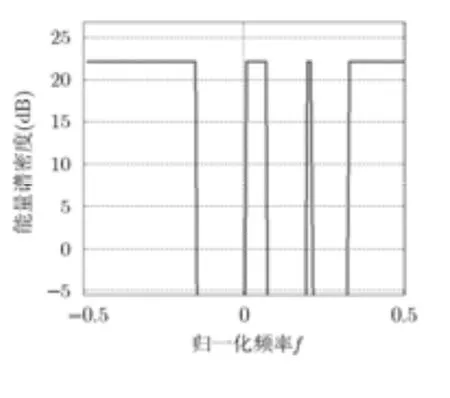
图 3 最优发射波形能量谱密度

图 4 固定权系数波形性能分析（PAPRMax=0.5 dB）

图 5 固定权系数算法阻带内积分能量随迭代下降曲线（仿真次数Q=1,10和50的平均值, M=100, PAPRMax=0.5 dB）

图 6 波形累积能量谱密度曲线 （波形长度M=20,50,100）

图 7 自适应权系数设计的波形能量谱（PAPRMax=0.5 dB, M=100）

下面主要讨论权系数w对阻带内积分能量和峰值的影响，图9给出了50次仿真平均值。从图9（a）可以看出，当固定权系数w在0～10 dB变化时，阻带内积分能量呈下降趋势，当超过10 dB时变化不显著，因此仿真中固定权系数选为10 dB。图9（b）给出了当阻带权系数定为10 dB条件下，峰值功率水平与峰值位置自适应权系数的关系，当自适应权系数超过20 dB时，峰值功率水平震荡起伏变化，因此仿真过程中自适应权系数选为20 dB是合理值。

表1给出了不同算法的运算量，由于引入SOCP模型，用标准内点法求解优化模型最差情况下的运算量为O（N3），本文算法运算量有所增加，所以该方法更适用于对波形频谱逼近程度要求较高的短波形设计或对实时性要求不高的长波形设计。

5 结论

本文提出了一种基于迭代凸优化的恒模波形合成方法，该方法将波形合成过程转化成PAPR约束下的优化问题，减少了迭代收敛次数，并利用频谱加权处理降低阻带功率水平，提高干扰及强杂波抑制能力，最后通过一系列变换操作将优化问题转化成二阶锥规划（SOCP）问题求解。所提方法在给定波形能量谱的条件下能够有效逼近理想的频谱形状，设计的波形具有恒模特性，并且适用于频谱形状较复杂的波形，最后通过计算机仿真验证了本文算法的有效性。

表 1 波形合成方法运算量比较

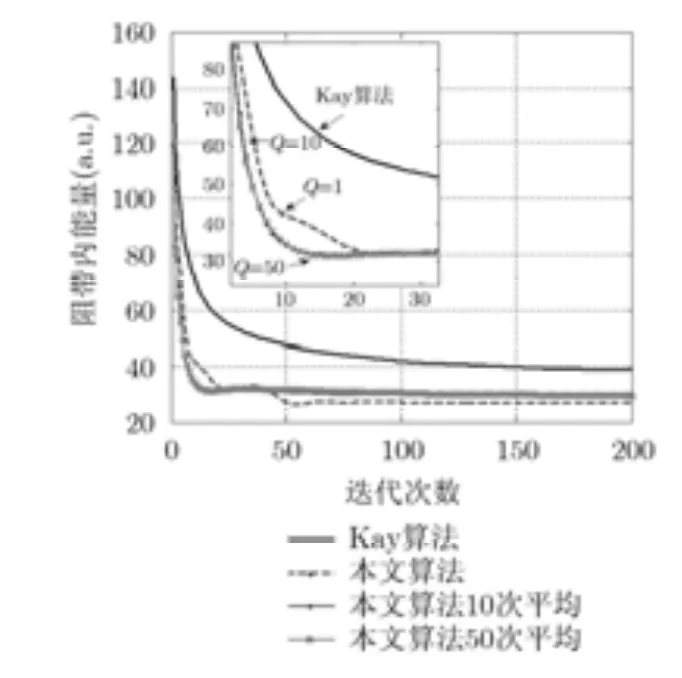
图 8 自适应权系数算法阻带内积分能量随迭代下降曲线（仿真次数Q=1, 10和50的平均值，M=100）

图 9 阻带内能量和峰值与 权系数关系

[1] Haykin S. Cognitive radar: a way of the future[J]. IEEE Signal Processing Magazine, 2006, 23（1）: 30-40.

[2] Sen S. PAPR-constrained pareto-optimal waveform design for OFDM-STAP radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52（6）: 3658-3669.

[3] Zhang X and Cui C. Signal detection for cognitive radar[J].Electronics Letters, 2013, 49（8）: 559-560.

[4] Aubry A, De Maio A, Jiang Bo, et al.. Ambiguity function shaping for cognitive radar via complex quartic optimization[J]. IEEE Transactions on Signal Processing,2013, 61（22）: 5603-5619.

[5] Aubry A, De Maio A, Farina A, et al.. Knowledge-aided（potentially cognitive） transmit signal and receive filter design in signal-dependent clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49（1）: 93-117.

[6] 公绪华, 孟华东, 魏轶旻, 等. 杂波环境下面向扩展目标检测的自适应波形设计方法[J]. 清华大学学报, 2011, 51（11）:1652-1656.Gong Xu-hua, Meng Hua-dong, Wei Yi-min, et al.. Adaptive waveform design for range-spread target detection in clutter[J]. Journal of Tsinghua University （Science &Technology）, 2011, 51（11）: 1652-1656.

[7] Bell M R. Information theory and radar waveform design[J].IEEE Transactions on Information Theory, 1993, 39（5）:1578-1597.

[8] Romero R A, Bae Junh-yeong, and Goodman N A. Theory and application of SNR and mutual information matched illumination waveforms[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47（2）: 912-927.

[9] Kay S. Optimal signal design for detection of Gaussian point targets in stationary Gaussian clutter/ reverberation[J]. IEEE Journal of Selected Topics in Signal Processing,2007, 1（1）: 31-41.

[10] Richards M A. Fundamentals of Radar Signal Processing[M].New York: The McGraw-Hill Companies, 2005: 230-231.

[11] Leland J, Steven K, and Naresh V. Iterative method for nonlinear FM synthesis of radar signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010,46（2）: 910-917.

[12] 赵宜楠, 李风从, 王军, 等. 基于秩亏傅里叶变换的交替投影编码波形设计[J]. 电子学报, 2014, 42（6）: 1216-1219.Zhao Yi-nan, Li Feng-cong, Wang Jun, et al.. Coded waveform design via alternating projection based on rank deficient Fourier transform[J]. Acta Electronica Sinica, 2014,42（6）: 1216-1219.

[13] 李风从, 赵宜楠, 乔晓林. 抑制特定区间距离旁瓣的恒模波形设计方法[J]. 电子与信息学报, 2013, 35（3）: 532-536.Li Feng-cong, Zhao Yi-nan, and Qiao Xiao-lin. Constant modular waveform design method for suppressing range sidelobes in specified intervals[J]. Journal of Electronics &Information Technology, 2013, 35（3）: 532-536.

[14] 赵宜楠, 张涛, 李风从, 等. 基于交替投影的MIMO雷达最优波形设计[J]. 电子与信息学报, 2014, 36（6）: 1368-1373.Zhao Yi-nan, Zhang Tao, Li Feng-cong, et al.. Optimal waveform design for MIMO radar via alternating projection[J]. Journal of Electronics & Information Technology, 2014, 36（6）: 1368-1373.

[15] Vescovo R. Reconfigurability and beam-scanning with phase-only control for antenna arrays[J]. IEEE Transactions on Antennas and Propagation, 2008, 56（6）: 1555-1565.

[16] Armstrong J. Peak-to-average power reduction for OFDM by repeated clipping and frequency domain filtering[J].Electronics Letters, 2002, 38（5）: 246-247.

[17] Wang Y C and Luo Z Q. Optimized iterative clipping and filtering for PAPR reduction of OFDM signals[J]. IEEE Transactions on Communications, 2011, 59（1）: 33-37.

[18] Boyd S and Vandenberghe L. Convex Optimization[M].Cambridge, United Kingdom: Cambridge University Press,2004: 340-341.

[19] Lobo M, Vandenberghe L, Boyd S, et al.. Applications of second-order cone programming[J]. Linear Algebra and Its Applications, 1998, 11（284）: 193-228.