基于多尺度分解的k邻域随机查找快速图像修复

廖 斌 苏 涛 刘 斌

1 引言

图像修复是指利用破损图像中完好区域的像素信息对破损区域进行修复处理，得到符合人类视觉要求的修复结果的过程[13]-。其在虚拟现实、游戏、影视、产品设计等领域有广泛的应用，是图像处理领域的一个研究热点。

Criminisi等人[4]提出基于样本块和优先级函数修复破损图像。通过计算破损区域边界上待修复像素点的优先级，确定像素点的修复顺序，达到增强修复效果的目的。但是，该方法使用乘积来定义优先级函数，导致其会出现突然降为零的现象，无法得到鲁棒的修复结果。Sun等人[5]通过用户交互指定未知区域的结构曲线信息，使之更好地传播，取得很好的修复效果。但是，该方法需要大量的人工交互，非常耗时。Wexler等人[6]提出一种基于样本块的多尺度[7]全局性时空修复方法。取出视频的单帧图像，并对其进行金字塔分层。从最粗糙层开始进行修复，并将像素信息映射到下一层直至取得最终的效果图。该方法中的块匹配过程采用暴力搜索，计算量很大，修复效果也不十分精确。为了加速块匹配计算，PatchMatch方法[810]-通过传播和随机查找以获取最佳的匹配块。相较于KD树[11,12]以及ANN（Approximate Nearest Neighbor）[13]，该方法有更好的加速比和更少的内存占用量。但是，其在查找匹配块的过程中会产生检索到冗余块的问题。

本文提出一种基于多尺度分解的k邻域随机查找快速图像修复方法。首先，基于双边滤波的下采样图像分解算法，对破损图像进行多尺度分解，得到一系列粗糙层。从最粗糙层开始，对当前层进行图像修复。然后，基于双边滤波上采样重建下一层。基于 k邻域（k-Nearest-Neighbor-Field, k-NNF）随机查找算法，对每一粗糙层查找与待修复块最相似的块。构建最小堆来存储k-NNF信息，有效避免检索到冗余块，提高查找速度。并且，采用一种鲁棒的优先级函数精确地获取块的修复顺序。

2 本文方法

设图像的完好区域为Φ，破损区域为Ω，破损边界为δΩ，边界的像素集合为S。首先，对破损图像I进行多尺度分解，得到一系列不同尺度的图像J[ i]（ i = 0,1,… ,l -1）。其中，原始图像为J[0]，最粗糙层为 J [ l - 1 ]。然后，使用k-NNF算法查找与S中任一点p为中心的待修复块Ψp的k个最相似块，进而从中计算出最佳匹配块。修复完成每一块后，都要更新优先级函数的置信因子，计算δΩ上像素点的优先级，确定需要修复的下一块。同时，更新Ω和S，直至 J [ i]中没有需要修复的Ω为止。最后，将修复结果的信息映射至下一层，重复上述修复过程，直至获得最终的结果。

2.1 图像的多尺度分解和重建

文献[14,15]中提到利用高斯金字塔对图像分解，获得其一系列粗糙层。但是，高斯滤波会造成图像边缘和细节信息的大量丢失，导致不能由分解得到的信息精确重建原始信息。从尽量减少信息丢失的角度考虑，本文提出一种基于双边滤波的下采样算子来对图像进行分解。双边滤波[16]是一种非线性的滤波方法，其综合考虑图像的空间域和范围域相似度，能够达到保边的效果，定义为

其中，（x, y）表示像素点的空间位置，（i, j）表示像素点（x, y）邻域 Δx,y内的像素点空间位置，BF （ x, y）表示滤波后的输出强度，IN（i, j）表示（i, j）的强度。w（i, j） 是双边滤波权， w （i, j ） = ws（i, j） wr（i, j ） ，其中，ws（i, j）为空间权，wr（i, j）为范围权，其表达式分别为

其中，δs表示空间域的标准差，δr表示范围域的标准差。

使用基于双边滤波的下采样算子对 J [ 0]进行滤波，然后隔行隔列下采样得到一个较粗糙的 J [ 1]。J [ 1]的尺寸变为 J [ 0]的1 4。如果对 J [ 0]作累进滤波，则会得到一系列不同尺度的粗糙层 J [ i]（ i= 1,2,…,l-1），如式（4）所示。

其中，“2↓”表示采样率为2的下采样操作。值得注意的是，虽然分解的层数越多，修复结果的细节越丰富，但是分解层数过多仍然会导致最粗糙层修复时损失大量信息，这在图像重建时无法恢复。因此，不宜选取过多的层数。本文取 5l= （即分解为4层）可以得到好的结果。为了可以实时地获取图像多尺度分解的结果，采用Yang等人[16]提出的快速双边滤波算法。该算法具有（）1O的时间复杂度，并可以采用GPU进一步加速。图1给出了一个图像分解示例。

图1 图像分解示例

从 [ ]1J l- 开始，根据后文提出的修复算法对每个 []J i进行修复。利用双边滤波的上采样算子对修复后的 []J i进行重建，把当前层的像素信息映射到重建层，如式（5）所示。

其中，“↑2”表示采样率为2的上采样操作。L（i）是第i层的高频因子，L（i）= J [ i] - Z * （ J[ i + 1 ] ）,i =

（↑2）0,1,…,l-1，其中，Z是一个模板。图2给出一个图像重建示例。

2.2 最佳匹配块搜索

图2 图像重建示例

在修复 []J i的过程中，关键是要获得高质量的样本块去覆盖待修复的块。首先，基于k-NNF算法在Φ中查找与pΨ相似度最高的k个匹配块，加速查找最相似块。同时，构造最小堆用于存储Ω中每一个Ψp的k-NNF信息，其包含k个匹配块中心像素点的空间位置和各匹配块与Ψp的相似度函数值。然后，利用最小堆的性质得出最佳匹配块以完成修复。

由此，定义映射函数为fi: gS（ Ψp） → gΦ（Ψq）,i=

1,2,…,k。该公式表示在S中任意一点p为中心的Ψp都将映射到Φ中与之相似的样本块Ψq，映射关系为

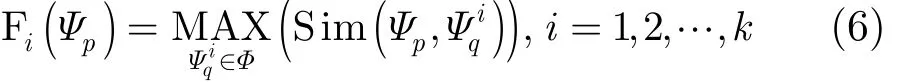
,δ是归一化因子。 D ist（ M , N）为两个尺寸同为w×w的块的颜色距离：

基于上述定义的映射函数，k-NNF由初始化、传播和随机查找3个步骤组成，如图3所示。

为图 3（a）中的初始化过程构建最小堆，如图 4所示。最小堆由k个结点组成，分别存储随机选取的k个块 Ψqi（A,B,C,…）的k-NNF信息（块中心像素点的空间信息和块间相似度）。建堆原则为父结点存储的块间相似度小于其两个子节点，如Sim（A, Ψp）≤Sim（B,Ψp） 且Sim（A,Ψp）≤ Sim（C,Ψp） 。其余结点依此类推。

图3 最佳匹配块搜索

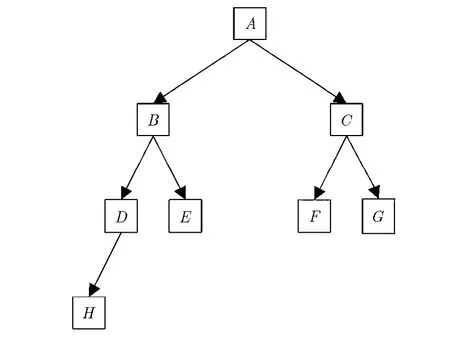
图4 初始化最小堆

初始化对应的k个块并不一定是相似度最好的候选块。为了找到相似度最高的k个块，执行传播过程如下。若当前处理以像素点（x, y）为中心的块Ψp，其相似块为fi（x, y），利用其相邻块 fi（ x - 1 ,y）和fi（ x, y -1）来优化修复 Ψp。由此，计算Sim（fi（ x, y ）,Ψp）, Sim（fi（x - 1,y ）, Ψp）, Sim（fi（x, y-1）,Ψp）来确定相似度最高的块，并用其空间位置信息更新fi（x, y），如图 3（b）所示。

根据 S im（fi（ x, y ）,Ψp） 与结点A所存储的块间相似度的大小关系来调整最小堆。如果前者小于后者，堆保持不变。否则，用fi（x, y）的k-NNF信息来更新A。然后，依据建堆原则调整堆，使其仍然保持为一个最小堆。该过程中，堆结点移动次数为logk。由此，可以最大程度地减少比较操作，同时可以减少内存访问，有助于提高运算速度。

在上述过程中，为了进一步提高搜索的准确度，得到更高相似度的匹配块，如图 3（c）所示，查找范围将呈指数级衰减，其计算如式（8）所示。

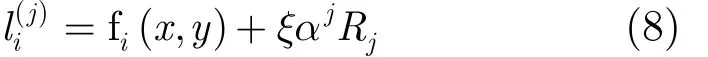
其中，ξ为最大查找半径， Rj是一个均匀分布于尺寸为[- 1, 1] ×[- 1,1]的窗口中的随机变量。α是固定衰减率，α=0.5。取j=1,2,…，直至ξαj衰减为一个像素。重复该过程，可以为Ψp快速收敛计算出更高相似度的匹配块。同时，在该过程中也要不断更新最小堆。

2.3 基于优先级函数的块选择

待pΨ修复完成后，基于优先级函数来确定下一个需要修复的块，包含如下3个步骤。

（1）块的优先级函数定义。设以p点为中心的块的优先级为（）Pp，则

其中，β是平衡因子。D（p）表示p点处的数据因子D （ p ）= |⋅np|/γ ，其中，γ 是归一化因子， ∇ I⊥p是等照度线向量，np是p点的单位法向量。CR（p）表示p点的置信因子， CR（p ） = （ 1 - t ） T （ p ） + t , 0＜t≤ 1，其中，t是用以控制曲线平滑的规范化因子，Ψp表示Ψp的面积。为了避免产生Criminisi算法中（）C p可能降为零导致优先级计算结果不鲁棒的问题，本文算法中（）CRp的值规范化于[ ],1t ，如图5所示。

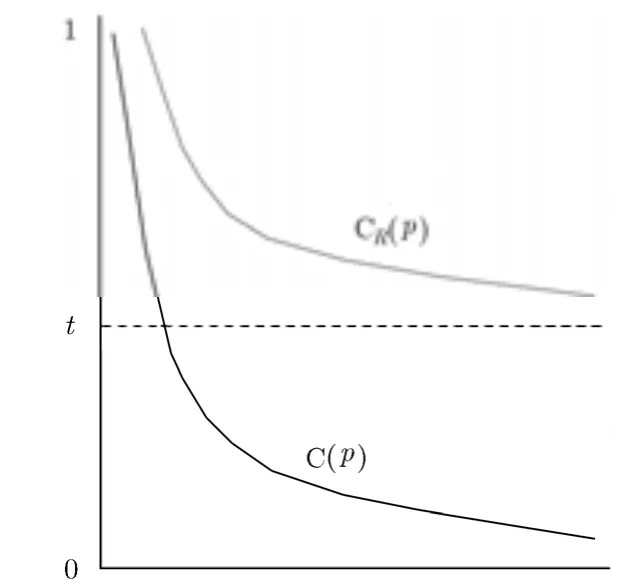
图5 置信因子比较

式（9）的初始化设置为T（p）=0,∀p∈Ω; T（ p）=1, ∀ p ∈I-Ω。同时，由于t控制置信因子曲线的平滑程度。如果t设置过大，则得到置信因子曲线将过于平缓，可能会得到相同的优先级函数值，无法确定一些像素点的修复顺序，导致修复质量降低。如果t设置过小，则得到置信因子的曲线变化较大，可能导致优先级函数值趋于零，同样影响修复质量。根据实验测算且不失一般性，本文对所有图像修复都选取 0.7t= 。

（2）块修复。根据2.2节最佳匹配块搜索算法来修复当前块。

（3）更新置信因子。如式（10）所示，

由此，优先级函数的置信因子更加合理，可信度更高。优先级函数的可靠性和有效性也得到了很好保证，能够得到质量更高的匹配块。

3 实验结果与分析

基于2.3 GHz 4核CPU, 4 GB内存的PC机硬件环境，采用 VS2010平台实现提出的算法。如图 6所示，给出了本文算法和 Criminisi算法以及Wexler算法的图像修复结果比较。

图6第1行 （尺寸为215182×）中，Wexler算法修复的效果不是很好，黑色和白色的边界线无法保持平滑，黑色和白色相互渗透。Criminisi算法基本上达到了修复效果，但是边缘信息不能很好地保持，并且白色区域还残留一些未修复的像素点。本文算法取得了更好的修复结果，很好地保持了边缘信息和纹理一致性。第2行（尺寸为206308×）中，本文算法修复后可以得到完整的细节。Criminis算法修复结果的小屋中间过渡不平滑，这主要是由于其优先级函数确定修复顺序不精确所导致。Wexler算法对该幅图像处理的效果更不好，未能有效修复破损区域。第3行（尺寸为375300×）中，对于Criminisi算法而言，由于每个小孩靠得的比较近，不能获取稳定的置信因子，导致了修复时无法得到好的效果。Wexler算法主要是因为暴力搜索得到的结果没有优化，传播过程也没优化，导致其他小孩的像素点干扰传播过程，所以修复结果也很不理想。本文算法修复结果的质量在整体上要好一些。第4行（尺寸为340508×）中，采用Criminisi算法修复得到的云的纹理不够自然。本文算法的修复结果更加符合人的视觉感受，修复后的图像中的云更加接近真实场景。Wexler算法修复后的图像中可以明显地看到一个不应该出现的方块。第5行（尺寸为1024801×）中，所对比的两种算法的修复结果依然残留有黑色像素。本文算法的修复效果明显更好，修复的区域和相邻的石山颜色保持一致。

为了客观地体现本文算法的性能，计算了所有待修复块覆盖区域的图像局部方差（Local Variance,LV）。如表1所示，本文算法修复结果的LV值小于其他两种算法，表明本文算法修复结果的质量更好，和人眼的视觉体验一致，客观上说明本文算法的有效性。

由表1可知，本文算法运行时间优于所对比的两种算法。尤其是破损图像的尺寸较大时，本文算法的优势更加明显。

同时，本文算法在执行效率方面存在场景依赖性。如图7所示，给出的两行图像尺寸大小一致（均为500300×），破损区域大小相同。但是，场景的复杂程度不同，第1行场景相对简单，而第2行场景较为复杂。通过测算得到第1行的修复时间为52.53 s，第2行的修复时间为112.38 s，可见不同场景对本文算法的执行效率有较大的影响。

表1 修复图像的LV值和运行时间（s）

图6 修复结果比较

4 结束语

本文提出一种基于多尺度分解的快速随机查找图像修复方法。基于双边滤波下采样算子分解图像，对粗糙层采用基于最小堆的k邻域随机查找算法以获取最优匹配块。基于鲁棒的优先级函数确定下一个待修复块。每一粗糙层修复后，用双边滤波上采样重建图像。与相关方法比较，本文算法具有更高的修复质量，执行速度快。未来的工作包括如何挖掘图像完好区域中潜在的图像信息，解决传播中误差积累的问题。

图7 不同复杂程度场景的图像修复示例

[1] He Kai-ming and Sun Jian. Image completion approaches using the statistics of similar patches[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36（12）:2423-2435.

[2] 许建楼, 冯象初, 郝岩. 改进的TV-Stokes图像修复模型及其算法[J]. 电子与信息学报, 2012, 34（5）: 1142-1147.Xu Jian-lou, Feng Xiang-chu, and Hao Yan. Improved TV-Stokes model and algorithm for image inpainting[J].Journal of Electronics & Information Technology, 2012, 34（5）:1142-1147.

[3] Guillemot C and Le Meur O. Image inpainting: overview and recent advances[J]. IEEE Signal Processing Magazine, 2014,31（1）: 127-144.

[4] Criminisi A, Pérez P, and Toyama K. Region filling and object removal by exemplar-based image inpainting[J]. IEEE Transactions on Image Processing, 2004, 13（9）: 1200-1212.

[5] Sun Jian, Yuan Lu, Jia Jia-ya, et al.. Image completion with structure propagation[J]. ACM Transactions on Graphic,2005, 24（3）: 861-868.

[6] Wexler Y, Shechtman E, and Irani M. Space-time completion of video[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29（3）: 463-476.

[7] 白键, 冯象初, 王旭东. 图像分解的多尺度变分模型[J]. 电子与信息学报, 2013, 35（5）: 1190-1195.Bai Jian, Feng Xiang-chu, and Wang Xu-dong. A multiscale variational model for image decomposition[J]. Journal of Electronics & Information Technology, 2013, 35（5）:1190-1195.

[8] Barnes C, Goldman D B, Shechtman E, et al.. The PatchMatch randomized matching algorithm for image manipulation[J]. Communications of the ACM, 2011, 54（11）:103-110.

[9] Zheng E, Dunn E, Jojic V, et al.. PatchMatch based joint view selection and depthmap estimation[C]. Computer Vision and Pattern Recognition （CVPR）, Ohio, 2014: 1510-1517.

[10] Cozzolino D, Poggi G, and Verdoliva L. Copy-move forgery detection based on PatchMatch[C]. IEEE International Conference on Image Processing （ICIP）, Paris, 2014:5312-5316.

[11] He Kai-ming and Sun Jian. Computing nearest-neighbor fields via Propagation-Assisted KD-Trees[C]. IEEE Conference on Computer Vision and Pattern Recognition（CVPR）, Judith, 2012: 111-118.

[12] Gieseke F, Heinermann J, Oancea C, et al.. Buffer k-d trees:processing massive nearest neighbor queries on GPUs[C].Proceedings of the 31st International Conference on Machine Learning, Beijing, 2014: 172-180.

[13] Zhang H, Berg A C, Maire M, et al.. SVM-KNN:discriminative nearest neighbor classification for visual category recognition[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York,2006: 2126-2136.

[14] Ran Ling-qiang and Meng Xiang-xu. Fast seam carving using Gaussian pyramid[C]. Intelligent Human-Machine Systems and Cybernetics （IHMSC）, Hangzhou, 2014: 59-63.

[15] Ren Shuai, Lei Jing-xiang, Zhang Tao, et al.. Research of high performance information hiding scheme based on Gaussian pyramid and CARDBAL2 multi-wavelet for secret communication[J]. International Journal of Applied Mathematics and Statistics, 2014, 52（6）: 234-251.

[16] Yang Q, Tan K H, and Ahuja N. Real-time O（1） bilateral filtering[C]. IEEE Conference on Computer Vision and Pattern Recognition, Florida, 2009: 557-564.