阵列通道不一致性误差快速有源校正算法

张 柯 程菊明 付 进

1 引言

在测向系统中，生产工艺、安装误差以及平台扰动等使传感器阵列产生幅相误差、阵元位置误差以及互耦现象，这将导致实际的阵列导向矢量与理想的阵列导向矢量有所不同。在这种情况下，常规的高分辨波达方向（Direction Of Arrival, DOA）估计技术，诸如最小方差无畸变响应（Minimum Variance Distortionless Response, MVDR[1]） ，多重信号分类（MUltiple SIgnal Classification, MUSIC[2]），旋转不变子空间（Estimation of Signal Parameters via Rotational Invariance Technique, ESPRIT[3]）和最大似然（Maximum Likelihood, ML[4]）等算法的测向性能将严重下降甚至失效。因此，在使用传感器阵列进行 DOA估计之前，阵列误差的校正工作是不可或缺的。

在阵列误差校正领域，众多国内外学者对阵列通道不一致所引起的幅相误差校正问题进行了深入的研究[511]-。文献[5]分析了通道幅相误差对MUSIC算法空域谱及分辨性能的影响，推导了存在幅相误差时 MUSIC算法空域谱的一阶统计表达式，揭示了幅相误差对 MUSIC算法空域谱影响的机理。文献[6]提出了一种基于独立成分分析法（Independent Component Analysis, ICA）的幅相误差盲校正算法，该算法需要较大的计算量且要求入射信源为非高斯信号。文献[7]利用阵列协方差矩阵同一对角线元素之间的幅相关系，提出了一种优化的幅相误差自校正算法，但该算法仅适用于线性阵列。文献[8]利用阵列输出矩阵及其共轭矩阵的Hadamard积构成新的协方差矩阵，并对其进行特征分解从而实现了幅相误差和DOA的联合估计，该算法无需迭代，避免了参数估计的局部收敛。与文献[8]原理相同，文献[9]利用阵列输出协方差矩阵及其共轭的Hadamard积构造新的协方差矩阵，然后由特征分解得到阵列幅相参数的估计值。与文献[7]相比，该方法拥有更高的阵列幅相参数估计精度，却需要更大的运算量。以上两种方法具有相同的应用条件：信源数目需大于2且不适用于线性阵列。上述几种算法都属于自校正算法，它们都需要较大的计算量和严格的限制条件，在实际工程应用中，有源校正算法由于计算量小、适用条件广仍然是最有效的校正手段。文献[10]提出了一种基于特征分解的实用的有源校正算法，该方法具有较高的阵列幅相参数估计精度，且在外场试验中得到了验证，但该方法需要较多的校正源且校正过程较为复杂。文献[11]提出了一个命名为传统数据模型估计算法（Estimation Algorithm for the Conventional Data Model,EACDM）的幅相误差有源校正算法。与其它有源校正算法相同，该算法也只利用了校正源的方位信息，在保证高精度参数估计性能的同时减小了计算量，但是由推导过程可以看出，该算法受信噪比和增益误差的影响很大，在信噪比较低或增益误差较大时，该算法的幅相参数估计性能将严重下降。

考虑有源校正为人工设置的信号源，可同时获得校正源的方位信息和波形信息，本文结合多级维纳滤波器[1214]-（MSWF），提出一种简化的阵列幅相误差快速校正的算法（SMSWF），与 EACDM 算法相比，SMSWF算法拥有更高的参数估计精度且计算量更小，其参数估计性能与特征分解法[15]基本相当。计算机仿真表明，单个已知信号波形的信号源入射到阵列时，SMSWF算法与特征值分解法有着相同的信号子空间估计能力。

2 阵列输出模型

假设M个标量传感器以间距d排列成线形阵列，放置于各向同性的噪声环境中，在以阵列轴线的法线为参考的 θk（k = 1 ,2,… ,K） 方向有K个波长为λ的远场窄带平面波入射。假设阵列的位置误差及互耦现象已被校正，即阵列只存在幅相误差，则阵列的输出模型为

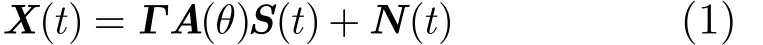
式中， X （t） = [x1（ t） ,x2（t） ,…,xM（t ）]T为M×1维观测的数据向量， S （t） = [s1（ t） ,s2（t） ,…,sK（t ）]T为零均值复高斯信号向量， N （t） = [n1（ t） ,n2（t） ,…,nM（t ）]T为M× 1 维零均值高斯白噪声向量。 A（ θ ）= [a （θ1）,a（θ2） , …,a （θK）]为理想的阵列流型导向矢量，其中a（θi）=[1,e-jωi, e-j2ωi, …,e-j（M-1）ωi]T, ωi =2π d sin（θi）/λ，定义Γ为包含幅相信息的M×M维对角矩阵：

式中，gi和φi（i = 1 ,2,…, M ）分别表示第i个阵元的增益和相位。本文中，信号与噪声相互独立。

3 MSWF简介及SMSWF算法的提出

3.1 MSWF快速求解信号子空间

多级维纳滤波器[11]是一种有效的降维滤波技术，其在最小均方误差的意义下得到维纳霍夫方程的渐近最优解而无需协方差矩阵的求逆。由式（1）可得阵列输出的协方差矩阵为：

而 Wiener-Hoof方程 R Wwf=rxd的渐进最优解为=，其中r为观测数据X （t ）与期望信号xdd0（t） 的互相关矢量：

式中，d0（t）为MSWF算法中的期望信号。MSWF的递推过程等价于在Krylov子空间 κm（R, r ）求解

xxdWiener-Hopf方程，经M级递推得到的各级匹配滤波器构成了M维 Krylov子空间 κm（R, r ）的一组xxd标准基。基于相关相减的MSWF是一种有效的多级维纳滤波结构，其迭代过程为

步骤1 初始化d0（t） 和y0（t） ；

步骤2 前向递推：令 i = 1 ,2,… , M ；

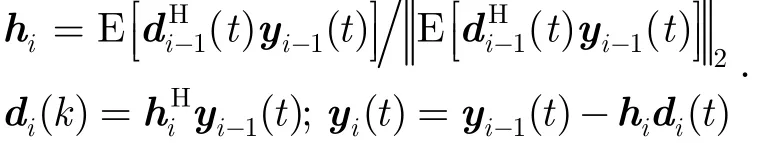
式中，d0（t ） 为训练信号或参考信号，y0（t） 为阵列输出，这种结构的 MSWF每级的运算量仅为O（ M N ）（其中M为滤波器长度，N为快拍数）。多级维纳滤波器已经被应用于实际的工程中[16]，文献[17]把多级维纳滤波器运用到阵列测向技术中，并证明：在给定某一期望信号的条件下，通过多级维纳滤波器可得到信号子空间和噪声子空间：

式中， h1,h2,… ,hM为维纳滤波器的各级匹配滤波器。

3.2 SMSWF算法的提出

在阵列的远场处放置一个窄带校正源s（）tS，其相对于阵列的方位是sθ，则阵列导向矢量为

式中， ω = 2π d sin（θs）/λ ，阵列的输出为

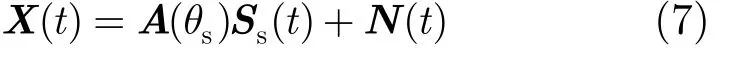
式中，

若同时获得校正源的方位及波形信息，取期望信号 d0（ t） = Ss（t） ，y0（t） = X （t ） ，则多级维纳滤波器的迭代过程可化简为

由式（5）知，

为进一步探究h和s（）θA之间的关系，对式（9）进行推导：

由式（8）、式（9）、式（11）和式（12）可得

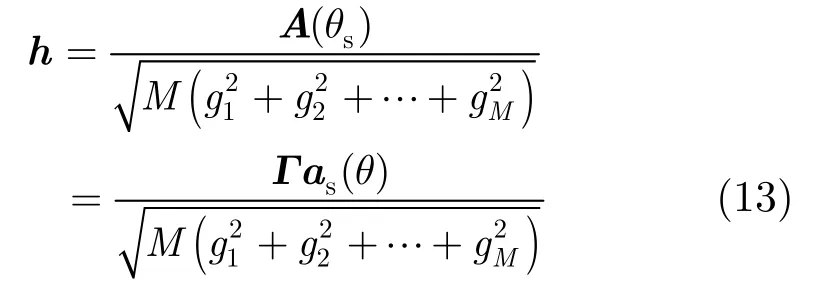
式（13）表明，h和A（θs）成正比，且比例系数是一个与阵元数目及阵元增益有关的量。

设h为h归一化后的值，则由式（13）可得第i（i = 1,2,… ,M ）个阵元Γi的估计值：

其中hi和ai（θs）分别为向量h和a（θs）中的第i个元素，由式（14）可得增益和相位的估计值为：

其中，i = 1 ,2,… , M 。运用得到的幅相误差估计值即可对阵列进行校正。

式（11）中，由于信号与噪声相互独立，可得到E[N （t（t） ]=0, 0为M×1维零矩阵，在实M×1M×1际情况中，由于快拍数有限，信号与噪声不可能绝对独立，故 E [N （t） SsH（t ）]是一个接近于0M×1的值，并且随着信噪比的增大和快拍数的增加趋于0M×1，故SMSWF算法的性能依旧会受到信噪比和快拍数的影响。由式（9）可以看出，SMSWF算法无需计算阵列协方差矩阵及进行特征分解运算，计算量仅为O（ M N ），而EACDM算法和特征分解法的计算量分别为 O （3M N） 和 O （ M2N + 4 M3/3）[11]，故 SMSWF算法对硬件的要求更低，更易于工程实现。另外，类似于特征分解法，SMSWF算法也可使用3个不同时出现的校正源（disjoint）对阵列的幅相误差和阵元位置误差进行联合校正。相比于EACDM算法和特征分解法只利用校正源的空域信息，SMSWF算法同时利用了校正源的空域信息和时域信息，这使得SMSWF算法计算量大为减小，同时拥有良好的参数估计性能。

4 计算机仿真

在以下仿真实验中，假设1个标量阵列沿x轴以/2dλ=等间距布放，阵元个数为8，校正源的中心频率为2000 Hz，带宽为40 Hz的窄带高斯信号，方位为30°，设第1个阵元为参考阵元，其增益和相位分别为g1=1和φ1=0，阵列增益误差为20%（相对于单位增益），即 gi（ i= 2 ,3,… , 8 ）服从（0.8,1.2）内的随机分布，相位 φi（i= 2,3,… ,8） 服从（-1,1）rad内的随机分布。

在表1和表2中，信噪比为20 dB，快拍数为200，3种算法的阵列增益和相位估计结果与真实值如表中所示，从表中可以看出，SMSWF算法与特征值分解法有着相似甚至相同的估计偏差，而EACDM算法的估计误差较大。

假设3个相互独立的等功率远场窄带信号入射到阵列，入射角度分别为15°, 20°和60°，信噪比为20 dB，快拍数为200，对未校正和运用3种算法校正后的阵列使用 MUSIC算法做空间谱估计，结果如图1所示。从图中可以看出，未校正时，MUSIC算法性能很差，不能分辨出两个角度相近的信号，

表1 增益的真实值和估计值

表2 相位的真实值和估计值（rad）

图1 校正前后的空间谱估计

且方位估计值存在较大的偏差。使用SMSWF算法和特征分解法校正后的 MUSIC空间谱几乎完全相同，优于 EACDM 算法。图 1（b）是图 1（a）中 G 处的放大图，由图中可以看出，使用SMSWF算法和特征分解法校正后，MUSIC算法能够准确的估计出信号的方位，而运用 EACDM算法校正后的方位估计结果存在0.1°的偏差。为比较 3种算法的幅相参数估计性能，定义增益和相位估计值的均方根误差分别为

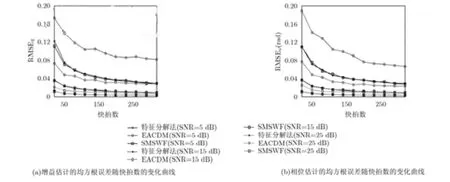
图2 幅相参数估计的均方根误差随快拍数的变化曲线

图2 表示不同信噪比条件下增益和相位参数估计的均方根误差随快拍数的变化曲线图，其中，横轴为快拍数，从20，间隔30，变化到320。从图中可以看出，SMSWF算法与特征分解法的幅相估计的均方根误差曲线几乎重叠在一起，而EACDM算法与SMSWF算法与特征分解法相比，其幅相参数估计的均方根误差较大，且信噪比越低，它们之间的差值就越大。这表明SMSWF算法与特征分解法拥有几乎相同的幅相参数估计能，远优于EACDM算法。

为了评价SMSWF算法和特征分解法获取信号子空间与理想的噪声子空间的正交性，定义两种算法的子空间正交系数如式（19）和式（20）所示。式中，Us和Vn分别为实际协方差矩阵和理想协方差矩阵特征值分解后得到的信号子空间和噪声子空间。其中理想协方差矩阵为无噪声时的阵列协方差矩阵，理想的子空间正交系数为 ηideal= 0 ，子空间正交系数的均方根误差定义为

图3分别为子空间正交系数均方根误差随快拍数和信噪比的变化曲线图，Monte Carlo次数为100，图 3（b）中，快拍数为 200。从图中可以看出，SMSWF算法与特征分解法子空间正交系数的均方根误差随信噪比和快拍数的增加而减小，在相同的信噪比和快拍数的情况下，SMSWF算法与特征值分解法的子空间正交系数均方根误差基本相同，这表明SMSWF算法获取的信号子空间等价于特征分解法得到的信号子空间，故两种算法对幅相参数的估计性能基本相同。上述仿真结果表明，若校正源波形已知，单源或分时工作信源阵列误差校正的特征分解过程均可由SMSWF算法替代。

5 消声水池试验

2013年 12月，在哈尔滨工程大学消声水池使用6元声压均匀线阵进行了幅相误差校正试验。使用丹麦BK公司生产的8103型标准声压水听器组成声压阵，阵元间距为0.075 m，声压阵与声源均处于水下2 m，声源是频率为10 kHz的单频信号，采样频率为51.2 kHz，声源与阵中心相距约11 m。阵列校正过程如下：设定校正源的方位为60°，快拍数为100，信噪比约为40 dB，取参考阵元的输出作为信号的波形信息，然后使用特征分解法和 SMSWF算法分别对声压阵进行校正。使用未校正的阵列和校正后的阵列，对方位为3°的声源测向，结果如图4所示。

在图4中，目标相对于声压阵的方位为3°。未校正时，声压阵 MUSIC谱线的峰值高度仅为 8.5 dB，方位估计值为5°；经过特征分解法和SMSWF算法校正后声压阵的 MUSIC谱线基本重合，校正后，MUSIC谱线峰值高度达到了15.5 dB，且方位估计值为3°。以上水池试验结果表明，SMSWF算法与特征分解法有着几乎相同的阵列校正性能，这与计算机仿真结果一致。

6 结束语

作为阵列信号处理的预处理过程，基于特征分解法的幅相误差有源校正算法计算量过大，不利于阵列信号处理的后续处理，本文提出一种快速实现阵列幅相误差校正的SMSWF算法。SMSWF算法计算量小，同时具有与特征分解法相同的幅相参数估计性能,计算机仿真和消声水池实验结果验证了SMSWF算法的优越性能。另外，SMSWF算法获取的信号子空间与特征分解法估计的信号子空间具有几乎相同的子空间正交系数，由此可得如下结论：单个已知信号波形的信号源入射到传感器阵列，阵列信号处理方法中的特征分解过程完全可以由SMSWF算法替代。

图3 不同信噪比和快拍数条件下，子空间正交系数的均方根误差的变化曲线图

图4 声压阵消声水池试验结果

[1] Pan Chao, Chen Jing-dong, and Benesty J. Performance study of the MVDR beamformer as a function of the source incidence angle[J]. IEEE Transactions on Audio, Speech and Language Processing, 2014, 22（1）: 67-79.

[2] 蔡晶晶, 鲍丹, 李鹏, 等. 强约束优化降维MUSIC二维DOA估计[J]. 电子与信息学报, 2014, 36（5）: 1113-1118.Cai Jing-jing, Bao Dan, Li Peng, et al.. Two-dimensional DOA estimation using reduced-dimensional MUSIC algorithm with Strong-constraint optimization[J]. Journal of Electronics & Information Technology, 2014, 36（5）:1113-1118.

[3] 马严, 陈伯孝, 杨明磊, 等. 基于ESPRIT的多基线分布式阵列 DOA 估计方法[J]. 系统工程与电子技术, 2014, 36（8）:1453-1459.Ma Yan, Chen Bai-xiao, Yang Ming-lei, et al.. Multi-baseline distributed array DOA estimation using ESPRIT algorithm[J]. Systems Engineering and Electronics, 2014,36（8）: 1453-1459.

[4] Shin Jong-woo, Lee Young-jun, and Kim Hyoung-nam.Reduced-complexity maximum liklihood direction-of-arrival estimation based on spatial aliasing[J]. IEEE Transactions on Signal Processing, 2014, 62（24）: 6568-6581.

[5] 王鼎, 王超, 吴瑛. 幅相误差对 MUSIC算法空间谱及分辨性能影响的分析[J]. 通信学报, 2010, 31（4）: 55-63.Wang Ding, Wang Chao, and Wu Ying. Analysis of the effects of the amplitude-phase errors on spatial spectrum and resolving performance of the MUSIC algorithm[J]. Journal on Communications, 2010, 31（4）: 55-63.

[6] Kim Jung-tai, Yang Hyun-jong, Jung Byung-wook, et al..Blind calibration for a linear array with gain and phase error using independent component analysis[J]. IEEE Antennas and Wireless Letters, 2010, 9（10）: 1259-1262.

[7] Li You-ming and Er M H. Theoretical analyses of gain and phase error calibration with opimal implementation for linear equispaced array [J]. IEEE Transactions on Signal Processing,2006, 54（2）: 712-723.

[8] Liu Ai-fei, Liao Gui-sheng, Zeng Cao, et al.. An eigenstructure method for estimating DOA and sensor gain-phase errors[J]. IEEE Transactions on Signal Processing,2011, 59（12）: 5944-5956.

[9] Cao Sheng-hong, Ye Zhong-fu, Xu Dong-yang, et al.. A hadamard product based method for DOA estimation and gain-phase error calibration[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49（2）: 1224-1233.

[10] Ng Boon-poh, Lie Joni-polili, Er Meng-hwa, et al.. A practical simple geometry and gain/phase calibration technique for antenna array processing[J]. IEEE Transactions on Antennas and Propagation, 2009, 59（7）: 1963-1972.

[11] Jiang Jia-jia, Duan Fa-jie, Chen Jin, et al.. Two new estimation algorithms for sensor gain and phase errors based on different data models[J]. IEEE Sensors Journal, 2013,13（5）: 1921-1930.

[12] 刘红明, 何子述, 夏威, 等. 无参考信号条件下基于MSWF的DOA 估计算法[J]. 电子学报, 2010, 38（9）: 1979-1983.Liu Hong-ming, He Zi-shu, Xia Wei, et al.. Estimation of direction of arrival based on MSWF without reference signal[J]. Acta Electronica Sinica, 2010, 38（9）: 1979-1983.

[13] 梁国龙, 张柯, 安少军, 等. 声矢量阵快速子空间方位估计算法[J]. 哈尔滨工业大学学报, 2014, 46（7）: 76-80.Liang Guo-long, Zhang Ke, An Shao-jun, et al.. Fast subspace DOA estimation algorithm based on acoustic vector sensor array[J]. Journal of Harbin Institute of Technology, 2014,46（7）: 76-80.

[14] 周柱, 张尔扬, 卢树军. 基于噪声子空间估计的MWF实现[J].宇航学报, 2012, 33（5）: 661-668.Zhou Zhu, Zhang Er-yang, and Lu Shu-jun. Implementation of MWF based on noise subspace estimation[J]. Journal of Astronautics, 2012, 33（5）: 661-668.

[15] 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京:清华大学出版社, 2004: 430-432.Wang Rong-liang, Chen Hui, Peng Ying-ning, et al.. Spatial Spectrum Estimation Theory and Algorithm[M]. Beijing:Tsinghua University Press, 2004: 430-432.

[16] 周天, 杨程, 李海森, 等. 基于AccelDSP的MM-MUSIC算法实现及其在多波束测深声纳中的应用[J]. 系统工程与电子技术, 2011, 33（12）: 2613-2617.Zhou Tian, Yang Cheng, Li Hai-sen, et al.. Realization of MM-MUSIC algorithm with AccelDSP and its application in multi-beam bathymetry sonar[J]. Systems Engineering and Electronics, 2011, 33（12）: 2613-2617.

[17] 黄磊, 吴顺君, 张林让. 基于多级维纳滤波器的信号子空间拟合算法[J]. 电子与信息学报, 2005, 27（8）: 1197-1200.Huang Lei, Wu Shun-jun, and Zhang Lin-rang. Signal subspace fitting based on the multi-stage wiener filter[J].Journal of Electronics & Information Technology, 2005, 27（8）:1197-1200.