隐函数存在定理的教学

张 杰，芮绍平

（淮北师范大学 数学科学学院，安徽 淮北 235000）

隐函数存在定理的教学

张 杰，芮绍平

（淮北师范大学 数学科学学院，安徽 淮北 235000）

隐函数存在定理是数学分析课程教学中的重点和难点.从引入、证明、应用以及推广4个方面对隐函数存在定理的教学进行探讨.

数学分析；隐函数存在定理；教学

数学分析的主要研究对象是函数，目标是研究函数性态，而隐函数是函数的一种重要表现形式.因此，隐函数存在定理成为数学分析的重点内容.由于该定理比较抽象，内容繁多，结构复杂，所以成为教学过程中的难点.笔者根据近几年数学分析课程的教学实践，就隐函数存在定理的教学，从以下几个方面谈一些体会和想法.

1 引入

以二元方程确定一元隐函数为例.为行文方便，将隐函数存在定理叙述如下：若函数F(x,y)满足：（1）F(x,y)在以P0(x0,y0)为内点的某区域D⊂R2上具有连续偏导数；（2）F(x0,y0)=0；（3）Fy(x0,y0)≠0，则方程F(x,y)=0在P0(x0,y0)点的某邻域上能唯一确定一个具有连续导数的函数y=f(x)，其定义域为x0的某邻域U(x0)，且导数为.

在该定理教学过程中，引入阶段很重要，引导方法正确、思路清晰，学生接受起来水到渠成.首先，举例说明并不是所有方程都可以确定隐函数，如方程y-x-1=0确定函数y=x+1，而y2+x2+1=0就不能确定任何函数关系，这样学生就理解了研究隐函数存在性的必要性.其次，由于实践中所遇到的一元函数大多数是定义在一个较大区间上的，所以学生对隐函数定理中隐函数定义在U(x0)不甚理解，从而导致对该定理充满神秘感，影响隐函数求导公式的运用.为解决这个问题，可以考虑方程x2+y2-1=0，一般都认同该方程确定了两个函数，即.其实，严格意义上应该叙述为：方程x2+y2-1=0在平面点集D1={( x,y)|-1＜x＜1,y＞0,x2+y2=1}上确定了函数y= 1-x2，类似地在平面点集D2={( x,y)|-1＜x＜1,y＜0,x2+y2=1}上确定了函数.在这个例子中，学生可能认为隐函数存在性的讨论不需要以点为单位，而可以在较大的平面点集如D1和D2上.此时，引导学生仔细观察点集D1和D2的相同点，容易发现点集D1只包含上半平面中的点，D2只包含下半平面中的点.那么在既含上半平面点又含下半平面点的点集上，方程x2+y2-1=0能确定隐函数y=f(x)吗？此时提出该问题，学生接受起来也很自然.分析如下：

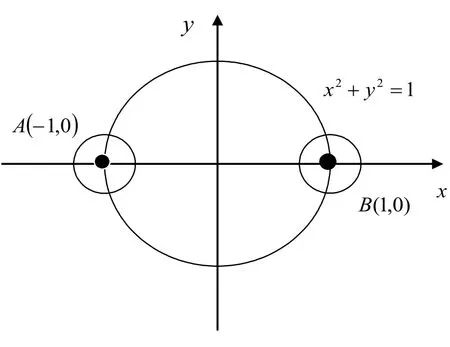
图1 方程x2+y2-1=0确定隐含数的情形

图1 中单位圆的圆周方程是x2+y2-1=0，在其上取两个特殊点A和B，这两点的任何邻域内既包含上半平面的点又包含下半平面的点，而在A和B的邻域内总会有一个x对应两个不同的y.也就是说，在A、B的邻域这个平面点集上，方程x2+y2-1=0不能确定隐函数y=f(x).此时可以得出结论：由于有A、B这样的点存在，所以隐函数存在性的研究应该以点为单位，而不是某个大范围上的.这样，学生对隐函数存在定理结论的局部性就有了一个清晰直观的理解，从而消除对定理的神秘感.

最后，影响学生理解该定理的是条件Fy(x0,y0)≠0，在证明中这个条件是为了保证函数F(x,y)关于变量y严格单调，但在证明前，可以做些铺垫工作，分析如下：若方程F(x,y)=0所确定的隐函数可导，则对方程两边同时关于x求导，有Fx(x,y)+Fy(x,y)y′=0，要解出y′，这里就要求条件Fy(x0,y0)≠0.当然，一般教材中关于此条件还有许多直观解释.

2 证明

有了上面引入工作，就可以进入定理的证明阶段.该定理的证明可以分成两大部分，即隐函数存在性和连续可微性，一般教材都有详细的证明过程［1］，这里需要指出的是，由于证明过程中反复应用连续函数的局部保号性，所以在证明之前要对连续函数的性质及其几何意义进行系统复习，以方便学生顺利掌握该定理的证明.

要讲清楚几个问题：（1）定理中条件仅仅是充分的.对于这一点可以例举方程y3-x3=0在(0 ,0)点由于，故不满足定理中的第三个条件，但该方程仍然能确定唯一连续可微函数y=x；（2）通过观察定理的证明过程，可以看出定理中的条件“在D内连续和”仅是为了保证函数F(x,y)关于变量y严格单调.因此定理的条件可以减弱为“F(x,y)在P0(x0,y0)的某邻域内关于y严格单调”；（3）考虑方程F(x,y)=0中两个变量地位对称，只要将定理中的条件Fy(x0,y0)≠0改为Fx(x0,y0)≠0，方程F(x,y)=0就能唯一确定一个以y为自变量的函数x=g(y)；（4）并不是所有的隐函数都可以显示化，如方程y-x-siny=0所确定的隐函数y=f(x)就不能被显示化；（5）研究隐函数存在定理有着重要意义，它使得我们又获得了一种函数的表达方式，甚至可以用来描述一个非初等函数，如由方程xy+2x-2y=0所确定的隐函数.

3 应用

隐函数存在定理在理论上应用广泛，这里主要讨论隐函数求导问题.根据隐函数存在定理，方程F(x,y)=0所确定的隐函数y=f(x)的导数为，在此基础上可以推导其二阶导数为（设F(x,y)存在二阶连续偏导数）.

在求导公式的实际使用中，不建议简单套公式，应该利用对方程两边同时求导的方法求解隐函数导数，如例1：

例1 验证方程F(x,y)=x2+y2-1=0在点(0,1)的某邻域内能确定唯一连续可微的隐函数y=f(x)，并求二阶导数.

解 由Fx(x,y)=2x，Fy(x,y)=2y,F(0,1)=0,Fy(0,1)=2≠0,据隐函数存在定理可知，方程x2+y2-1=0在点(0,1)的某邻域内能确定唯一连续可微的隐函数y=f(x).

对方程x2+y2-1=0两边同时关于x求导，有2x+2yy′=0，，再对2x+2yy′=0两边同时关于x求导，得2+2y′y′+2yy″=0，从而.

隐函数在求极值问题中的应用也是值得注意的一个问题，一般教材中都有提及，可以适当补充例题来讲清楚该问题.

例2 求函数z=xy在约束条件x+y=1下的极值.

解 应用拉格朗日乘数法，令L(x ,y,λ)=xy+λ(x +y-1)，求偏导数，并令其等于0，有

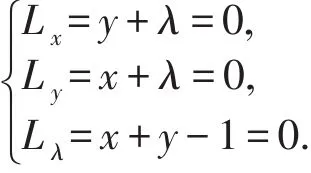
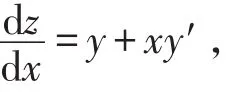
其中y′可以看做是方程F(x,y)=x+y-1=0所确定隐函数的导数，故

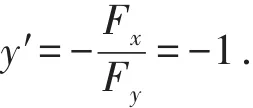
从而

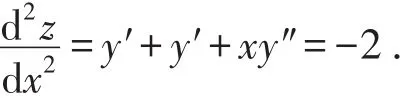
隐函数存在定理在实际生活中的应用也非常广泛，如优化问题中的应用［2］、生物科学中的应用［3］以及物理学中的应用等.学生就会充分认识到学习该定理的重要性，从而激发学生主动探究新知识的学习热情，学习效果和效率自然会提高.

4 推广

作为隐函数存在定理知识体系的一部分，其推广工作也是重点和难点.在推广过程中，学生的知识得到进一步完善形成一个整体，达到事半功倍的效果.具体来讲，该定理可以横向和纵向推广.

纵向就是教材中的推广工作，也就是将二元方程确定一个隐函数的情形推广至三元方程F(x,y,z)=0确定一个二元隐函数的情况，进而推广至n+1个变量方程确定隐函数的情形，最后利用函数行列式推广至方程组确定隐函数组的情形.具体推广过程请详见教材［1］.

对隐函数存在定理（二元方程确定一个隐函数的情形）横向推广一般考虑两个方面，也就是条件和结论.由于原定理中的条件是充分非必要的，因此适用范围具有局限性，一些文献［4-5］就对隐函数存在定理的条件进行了相关推广.对于结论，由于原定理的结论具有局部性（在邻域内讨论存在性），所以推广工作主要集中在延拓方面，也就是将隐函数的存在性由局部拓展至某个大范围上，这方面的文献可参见［6-7］等.

5 总结

通过以上分析，可以让学生了解隐函数存在定理的来龙去脉，构建一个完整知识块系，帮助学生轻松掌握难点问题，从而提高他们的学习热情.在实际教学实践中，还可以结合微课设计，将该定理的教学分解成几个微课片段，分散难点，鼓励学生主动访问各大名校的有关MOOC视频，从而达到更好的学习效果.

［1］华东师范大学数学系.数学分析（下册）［M］.北京：高等教育出版社，2001.

［2］袁亚湘，孙文瑜.最优化理论与方法［M］.北京：科学出版社，2010.

［3］杨强大，王福利，常玉清.基于阶段识别的诺西肽发酵过程软测量建模［J］.仪器仪表学报，2008，29（8）：1779-1783.

［4］钱传喜.隐函数定理的一个推广［J］.扬州师院学报（自然科学版），1988，8（1/2）：11-15.

［5］杜继宏，冯元琨，李春文，等.隐函数存在的充分条件［J］.清华大学学报，1999，39（1）：75-78.

［6］罗时健.关于隐函数存在定理的注记［J］.黔东南民族师专学报，1996（Z1）：5-7.

［7］黄松琴，廖晓昕.关于非局部隐函数存在定理的一点注记［J］.华中师院学报（自然科学版），1981，10（2）：42-48.

Research on Teaching of Implicit Function Theorem

ZHANG Jie，RUI Shaoping
（School of Mathematical Science，Huaibei Normal University，235000，Huaibei，Anhui，China）

Implicit function theorem is an emphasis and difficulty of in the teaching of mathematical analysis. In this paper，we do some preliminary exploration from four aspects which are guidance，proof，application and generalization.

mathematical analysis；implicit function theorem；teaching

O 17

C

2095-0691（2015）04-0093-04

2015-05-08

安徽省质量工程教研项目（2015jyxm165）；淮北师范大学教学研究项目(jy15106,jy13230）

张 杰（1979- ），女，安徽淮北人，硕士，副教授，研究方向：优化理论.