碳纤维复合材料汽车翼子板优化设计研究
2015-12-09程章朱平冯奇何健周庆伟
程章++朱平++冯奇++何健++周庆伟
摘 要:碳纤维复合材料(carbon fiber reinforced plastic,CFRP)零件的性能与其结构形式和铺层方式相关,合理的结构设计及铺层方式可充分发挥CFRP的效能。以CFRP汽车翼子板为研究对象,在保证性能要求的前提下,采用自由尺寸优化方法进行翼子板结构优化设计。在此基础上,将拉丁超立方采样与有限元方法相结合,获得翼子板设计空间的初始样本数据,建立以安装点刚度为目标的Kriging模型,并利用期望改进准则不断提高模型精度。基于构建的Kriging模型,采用遗传算法求解翼子板最佳铺层方式,使优化后的 CFRP翼子板减重效果达到43.1%。
关键词:碳纤维复合材料;翼子板;结构优化;铺层优化;Kriging模型
中图分类号:U463.83+9.2文献标文献标识码:A文献标DOI:10.3969/j.issn.2095-1469.2015.05.09
CFRP具有比强度高、比模量高、碰撞吸能性好、耐疲劳等特点,在汽车行业应用广泛。由于其各向异性的力学特性,CFRP的结构形式和铺层方式都会对其性能产生影响。合理的结构形式和铺层方式能够在减轻结构重量的情况下提高结构的力学性能,因此CFRP零件优化设计具有重要意义。CFRP零件由单层复合材料铺叠而成,可制造性要求铺设角度只能从标准的角度中选取,因此CFRP优化为离散变量优化问题。且汽车车身结构复杂,CFRP翼子板优化问题难度较大。
随着CFRP应用的推广,国内外学者开展了大量CFRP零件优化设计的研究。Wu Jun等人[1-2]研究了传动轴、矩形平板等简单CFRP结构的铺层优化方法。乔巍等人[3-6]基于遗传算法对机翼、风机叶片等结构进行铺层角度或铺层顺序的优化设计,得到结构的最优铺层方式。严君等人[7-8]利用自由尺寸优化方法进行了零件结构形式的优化设计。
目前,自由尺寸优化法已成为CFRP结构优化设计的主要方法,但忽略了制造工艺限制,与工程实际联系不紧密。对于CFRP铺层优化的研究主要集中于矩形板、传动轴、叶片等简单结构,目标函数与铺层方式的函数关系可通过理论推导获得或可利用有限元软件直接计算求解最优铺层方式。然而,CFRP车身零件一般为复杂曲面结构,其刚度、强度等性能指标与铺层方式之间的函数关系难以获得,利用有限元软件直接计算时间较长,因此对于CFRP复杂车身结构的铺层优化问题,关键在于目标函数的建立。
本文以CFRP翼子板为研究对象,利用自由尺寸优化方法,进行翼子板结构优化。在此基础上,将拉丁超立方采样与有限元方法相结合,获取设计空间初始样本点及其响应,针对翼子板铺层优化问题,建立翼子板安装点刚度响应与铺层方式近似计算的Kriging模型,并采用期望改进准则(Expected Improved Function,EI)不断提高模型精度。根据构建的Kriging模型,应用遗传算法求解CFRP翼子板的最佳铺层方式,完成翼子板优化设计,并进行仿真分析验证。
1 翼子板结构优化设计
作为车身承力结构件,翼子板必须具有一定承受载荷和抵抗变形能力,其性能要求如下:(1)外板刚度:初始刚度≥30 N/mm,施加220 N后变形≤7.5 mm;(2)抗凹性:施加150 N的力后,永久变形≤0.15 mm;(3)翼尖刚度:翼子板翼尖刚度≥50 N/mm;(4)翼子板安装点刚度:翼子板安装点刚度≥50 N/mm。
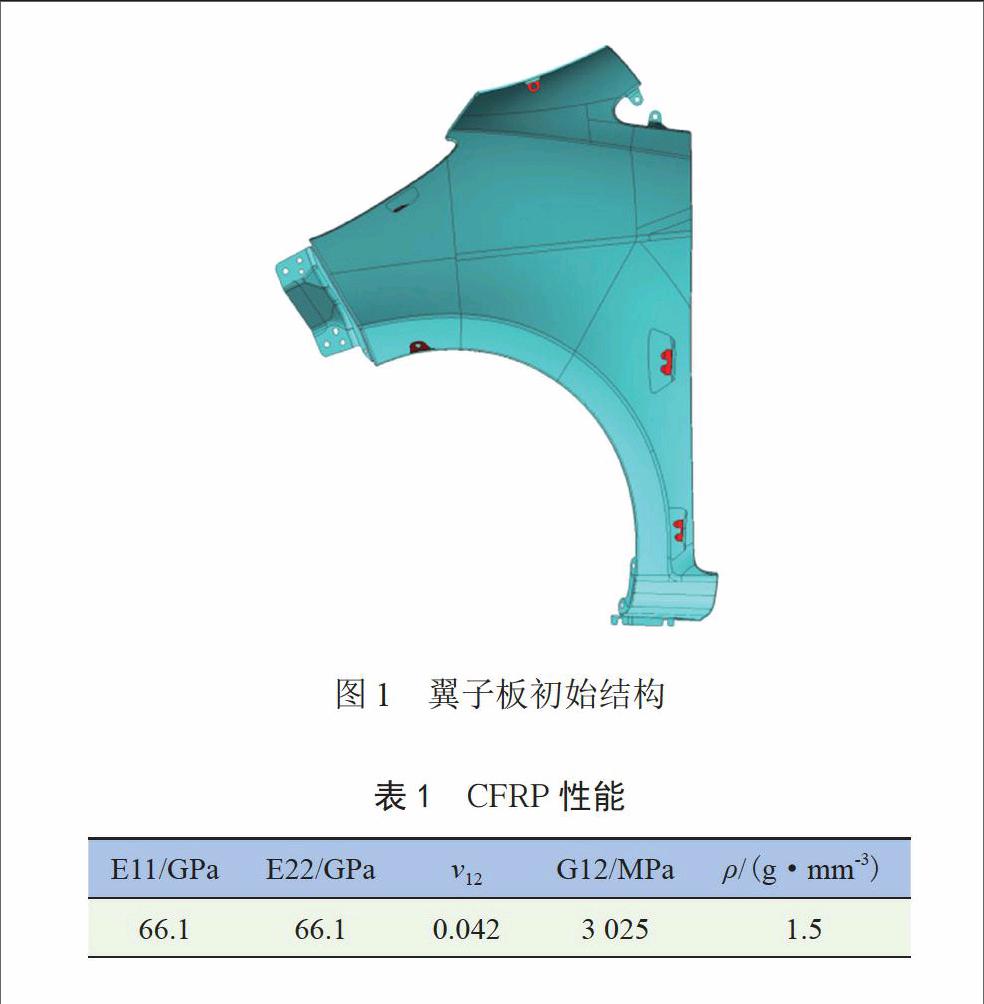
翼子板结构如图1所示,厚度为4 mm,重量为2.274 kg。制备翼子板所使用材料为平纹机织CFRP,其单层厚度为0.2 mm,材料强度为300 MPa,性能见表1。翼子板初始铺层为[0/45/90/
-45]5S,通过Abaqus软件仿真计算得到翼子板各性能均满足要求,且除安装点刚度外其它性能远远超过要求,表明翼子板存在很大的优化设计空间。
应用优化设计方法进行翼子板结构轻量化设计,可以在保证翼子板性能要求的前提下,提高材料的利用率,实现汽车轻量化和控制成本的目的。在现有翼子板结构基础上进行结构优化设计,需保持翼子板造型面不变,因此选择板厚作为设计变量。为达到轻量化的目的,选择翼子板质量作为目标函数,选择翼子板各性能要求作为约束条件。优化后翼子板结构不仅要满足性能要求,同时需要考虑结构的可制造性要求。
基于性能要求和制造工艺限制的翼子板约束优化问题可表述为
。
式中,x为翼子板板厚,CFRP层合板制造时最小厚度为0.2 mm,即单层CFRP厚度,最大厚度不超过7.5 mm;为翼子板质量函数,由零件板厚、面积和材料密度决定,优化计算的目标为翼子板质量最小;gi(x)为翼子板刚度约束,包括外板刚度、安装点刚度等,在以有限元模型为基础的优化计算中,通过设定相应点的最大变形量来确保刚度满足要求;h(x)为复合材料的强度要求。
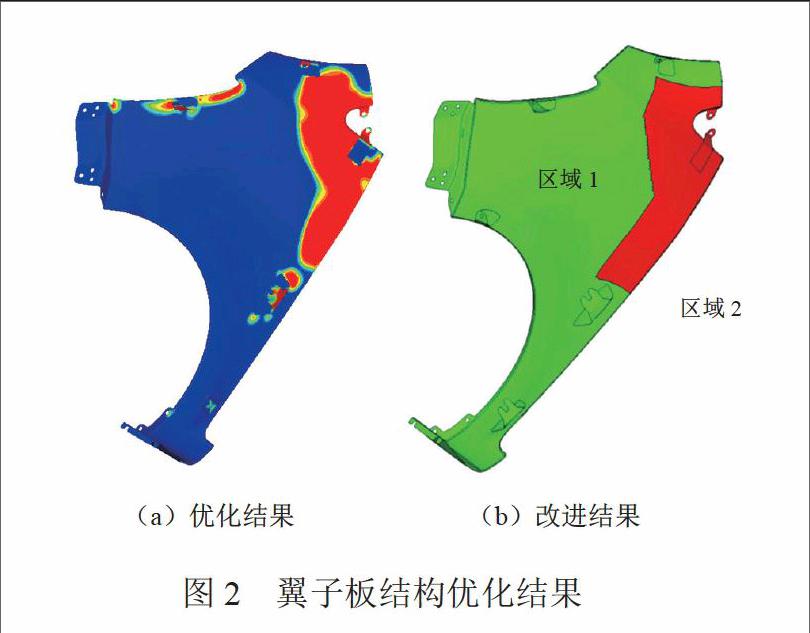
采用Optisturct软件中的自由尺寸优化方法进行CFRP翼子板的结构优化设计,结果如图2(a)所示。根据设计经验并考虑制造工艺,修整改进优化结果,将翼子板按厚度划分为两个区域,使其适合生产要求,得到翼子板结构如图2(b)所示。由图可以看出,改进后翼子板的造型面及安装面保持不变,以保证翼子板外形及正常装配;翼子板厚度发生变化,以便在减轻重量的同时满足性能要求,其中区域1(图中绿色部分)厚度为1.8 mm,区域2(图中红色部分)厚度为3.8 mm,重量为1.294 kg。
为验证优化后翼子板结构的可行性,对改进优化结构进行性能评估,区域1初始铺层为[0/45/90/ -45/]S,区域2初始铺层为[0/45/90/-45/02/45/90/ -45/02/-45/90/45/0]T,计算结果见表2。
由表2可以看出,优化后翼子板各性能均满足性能要求,说明优化后翼子板结构设计满足要求。但结构优化后的翼子板安装点刚度值与要求非常接近,制造偏差可能导致安装点刚度不满足要求,因此应在结构优化基础上进行铺层优化设计,以提高安装点刚度。
2 翼子板铺层优化设计方法
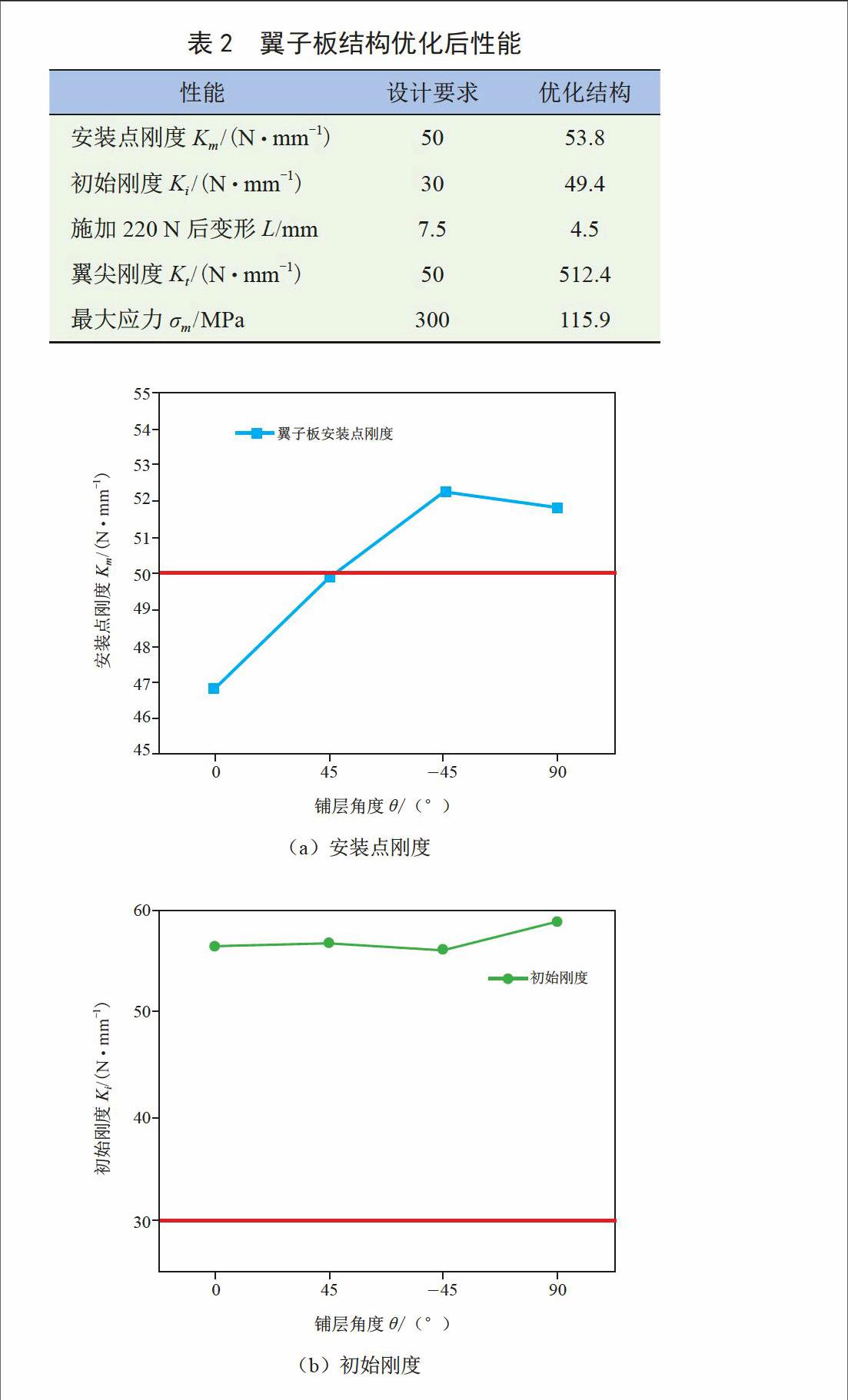
为研究铺层角度对翼子板性能的影响,设置翼子板区域1和区域2的铺层角度分别全为0°,45°,-45°和90°。利用Abaqus软件计算CFRP翼子板在这些铺层情况下的性能响应,结果如图3所示。
由图3可知:(1)不同铺层角度对翼子板安装点刚度有较大影响,不合理的铺层方式可能导致安装点刚度不满足要求,其中-45°铺层对安装点刚度增强作用最大。(2)除安装点刚度性能外,翼子板在0°,±45°和90°四种铺层角度情况下的初始刚度、翼尖刚度等性能远远超过标准要求,铺层角度对这些性能的影响较小,铺层角度变化不会导致翼子板失效。因此,选择安装点处刚度作为优化目标,以其它性能要求为约束,寻找CFRP翼子板的最佳铺层顺序,在保证翼子板各性能均满足设计要求情况下,尽可能发挥材料的效能。
由于翼子板结构复杂,安装点刚度与铺层方式的函数关系无法通过公式推导获得。如果利用有限元软件结合遗传算法计算每个子代的刚度响应,会导致计算时间过长,不符合实际要求。Kriging方法作为一种高效的近似建模技术,由于响应预测快,可重复性高等特点,已经广泛应用于结构优化设计中[9-13]。Kriging建模方法可根据一定数量的样本点,建立目标函数的高精度代理模型,从而将复杂的物理问题转化成容易计算的数学问题。本文利用Kriging模型拟合目标函数,为遗传算法求解优化问题奠定基础,整个铺层优化设计流程如图4所示。
5 结论
本文以CFRP翼子板为对象,研究了CFRP复杂零件优化设计方法流程。利用自由尺寸优化方法进行CFRP翼子板的结构设计。在优化的翼子板结构基础上,将拉丁超立方采样和有限元方法相结合获取初始样本数据,构造了安装点刚度与铺层方式的Kriging模型;引入期望改进准则不断改进模型精度,得到满足计算精度要求的Kriging模型;基于构造的Kriging近似模型,利用遗传算法完成翼子板铺层优化,得到最佳铺层顺序。计算结果表明,结构优化后翼子板重量减轻43.1%,铺层优化后较之前翼子板安装点刚度提高了12.3%,为CFRP汽车零部件轻量化设计提供了可借鉴的方法。
参考文献(References):
Wu Jun,BURGUE?O R. An Integrated Approach to Shape and Laminate Stacking Sequence Optimization of Free-Form FRP Shells [J]. Computer Methods in Applied Mechanics and Engineering,2006(195):4106-4123.
MONTAGNIER O,HOCHARD C. Optimization of Hy-brid High-Modulus/High-Strength Carbon Fiber Reinforced Plastic Composite Drive Shafts [J]. Materials and Design,2013(46):88–100.
乔巍,姚卫星. 复合材料加筋板铺层优化设计的等效弯曲刚度法 [J]. 计算力学学报,2011,28 (1): 158-162.
Qiao Wei,Yao Weixing. Equivalent Bending Stiffness Method for Stacking Sequence Optimization of Composite Stiffened Panel [J]. Chinese Journal of Computational Mechanics,2011,28(1):158-162.(in Chinese)
韩庆,王广博,钟小平,等. 基于遗传算法的复合材料泡沫夹层板铺层优化设计 [J]. 航空工程进展,2013,4(2):182-185.
Han Qing,Wang Guangbo,Zhong Xiaoping,et al.
Ply Optimization Design of Foam Sandwich Composite Panel Based on Genetic Algorithm [J]. Advanced Aero-nautical Science and Engineering,2013,4(2):182-185.(in Chinese)
周磊,万志强,杨超. 复合材料壁板铺层参数对大展弦比机翼气动弹性优化的影响 [J]. 复合材料学报,2013,30(5):195-200.
Zhou Lei,Wan Zhiqiang,Yangchao. Effect of Laminate Parameters of Composite Skin on Aero-elastic of High-Aspect-Ratio Wing [J]. Acta Material Composite Sinica,2013,30(5):195-200.(in Chinese)
冯消冰,黄海,王伟. 大型风机复合材料叶片铺层优化设计 [J]. 玻璃钢/复合材料,2013(3):3-7.
Feng Xiaobing,Huang Hai,Wang Wei. Ply Optimization of Composite Material for the Blade in Wind Turbine [J]. FRP/CM,2013(3):3-7. (in Chinese)
严君,杨世文. 基于Optistruct的碳纤维复合材料包装箱结构优化设计 [J]. 玻璃钢/复合材料,2012(2): 12-16.
Yan Jun,Yang Shiwen. Structure Design of Carbon Fiber Composite Package-Case Based on Optistruct Optimization Technology [J]. FRP/CM,2012(2):12-16.(in Chinese)
朱胜利,刘红武,邱宏波. 基于复合材料机翼刚度的铺层自由尺寸优化分析 [J]. 航空工程进展,2012,3(1):55-59.
Zhu Shengli,Liu Hongwu,Qiu Hongbo. Free-Size Optimization Analysis of Composite Ply Based on the Stiffness of the Composite Wing [J]. Advanced in Aero-nautical Science and Engineering,2012,3(1):55-59. (in Chinese)
JEONG S,MURAYAMA M,YAMAMOTO K. Efficient Optimization Design Method Using Kriging Model [J]. Journal of Aircraft,2005,42(2):413-420.
SAKATA S,ASHIDA F,ZAKO M.An Efficient Algo-rithm for Kriging Approximation and Optimization with Large-Scale Sampling Data [J]. Computer Methods in Applied Mechanics and Engineering Data,2004,193 (3): 385-404.
黄章俊,王成恩. 基于Kriging模型的涡轮盘优化设计方法 [J]. 计算机集成制造系统,2010,16(5):905-910.
Huang Zhangjun,Wang Cheng'en. Turbine Discs Optimi-zation Designed Based on Kriging Model [J]. Computer Integrated Manufacturing System,2010,16(5):905-910.(in Chinese)
JONES D R,SCHONLAU M,WELCH W J. Efficient Global Optimization of Expensive Black-Box Functions [J]. Journal of Global Optimization,1998,13(4):455-492.
许瑞飞,宋文萍,韩忠华. 改进Kriging模型在翼型气动优化设计中的应用研究 [J]. 西北工业大学学报,2010,28(4):503-509.
Xu Ruifei,Song Wenping,Han Zhonghua. Application of Improved Kriging-Model-Based Optimization Method in Airfoil Aerodynamic Design [J]. Journal of Northwestern Polytechnical University,2010,28(4):503-509.(in Chinese)
