基于教材感悟思想导向思维——一道源于教材的中考试题命题的实践与思考

●傅瑞琦(金华市教育局教研室浙江金华321000)

基于教材感悟思想导向思维
——一道源于教材的中考试题命题的实践与思考

●傅瑞琦(金华市教育局教研室浙江金华321000)

试题设计一直重视教材资源的应用和拓展，特别是试卷中的关键试题.由于承担着考查学生探究能力、实践能力和创新能力等数学素养的重任，更需要立足教材，依据教材素材，改编形成试题，力求在学习经验积累、问题解决能力以及数学潜能上对学生适度区分，达到对“数学深层思维”的考查目的.现以2014年数学中考金华卷第24题的命制过程，浅谈如何利用教材资源，探讨压轴题编制的尝试与完善.

1 教材素材

根据命题计划，最后一题的素材选自教材.我们期望，一是背景设计为学生熟悉;二是考查内容选自数学核心知识的交汇处;三是改编为具有开放性、动态探究相结合的综合性问题，将观察、探究和计算有机融合，综合考查学生灵活应用所学知识和经验去分析问题、解决问题的能力.

素材已知:如图1，P是∠AOB内一点，PD⊥OA，PE⊥OB，D，E分别是垂足，且PD=PE.求证:点P在∠AOB的平分线上.

图1

素材解读这是浙教版八年级上册2.8节“直角三角形全等的判定”中的范例，通过应用直角三角形全等的判定方法，得出角平分线性质定理的逆定理.若联结DE，则△PDE是等腰三角形.

改∠AOB为钝角，点P是一动点，研究△PDE是等腰三角形的存在性问题.

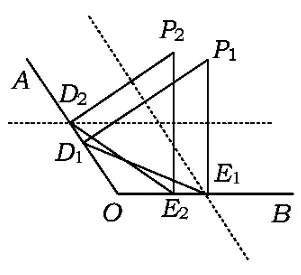
图2

图3

图4

1)若△PDE是等腰三角形，点P的位置除了在∠AOB平分线上外，还有2种情况(如图2):当DP=DE时，点D在线段PE的中垂线上;当EP= ED时，点E在线段PD的中垂线上.

2)若∠AOB=120°(如图3)，则△PDE是正三角形.

3)若∠AOB=135°，除了∠AOB的角平分线上的点P外(如图4)，还存在△PDE是等腰直角三角形2种情况.

结合上面的分析，将背景放置在直角坐标系中，对点P的位置给出一定的限定，寻找隐含在其中的几何基本图形，让学生对等腰三角形的存在性问题进行探究，形成初稿分析考查的可行性.

2 研究过程

初稿在平面直角坐标系中，直线l:y=-x-4与x轴交于点E，过抛物线上的点P分别作x轴、直线l的垂线，垂足为E，F，当△PEF为等腰三角形时，试求点P的横坐标.

分析设点P的横坐标为t.如图5，△PEF是等腰直角三角形，有t1=-4;如图6，△PEF是等腰直角三角形，与x轴成45°角的直线PF与抛物线的交点有P2和P3这2种情况，直线PF的解析式为y=x+4，由，解得

图5

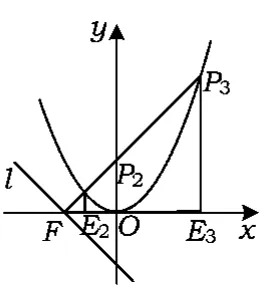
图6

图7

如图7，点P在∠ODF的角平分线上，过点F作FH⊥PE，由，得方程

但该方程的一次项系数、常数项都含有根式，求解已经超出课标要求.

调整直线l的位置，并将抛物线改为双曲线形成第2稿.

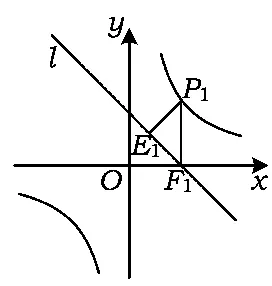
图8

图9

图10

分析如图8，△PEF是等腰直角三角形，可以求得点P1的横坐标为.如图9，△PEF是等腰直角三角形有2种情况，设P1F2=F2E=t，则

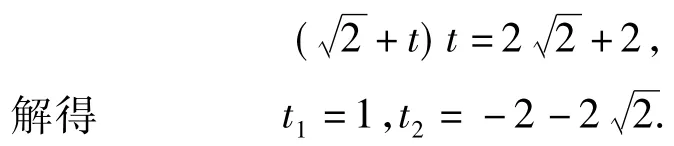
如图10，点P在角平分线上，延长P4F4，交直线l于点H，设DF4=DE4=t，则

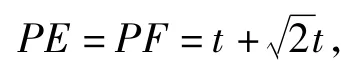
另外，从图形看，点P的位置是直线l与x轴夹角平分线与抛物线或双曲线的交点，求2个图像的交点坐标即为点P的坐标，计算复杂，方法单一.

因此，基于选择抛物线、双曲线都会出现超标的方程，因此改为直线型图形就可以避免这种情况，于是形成第3稿(定稿).

3 定稿分析

定稿如图11，直角梯形ABCO的2条边OA，OC在坐标轴的正半轴上，BC∥x轴，OA=OC=4，以直线x=1为对称轴的抛物线过点A，B，C.

1)求该抛物线的函数解析式.

2)已知直线l的解析式为y=x+m，它与x轴交于点G，在梯形ABCO的一边上取点P.

①当m=0时，如图11，点P是抛物线对称轴与BC的交点，过点P作PH⊥直线l于点H，联结OP，试求△OPH的面积.

②当m=-3时，过点P分别作x轴、直线l的垂线，垂足为点E，F.是否存在这样的点P，使以P，E，F为顶点的三角形是等腰三角形?若存在，求出点P的坐标;若不存在，请说明理由.

图11

图12

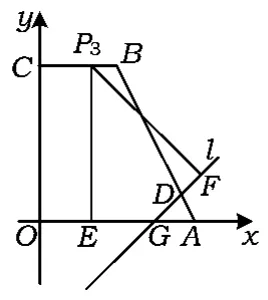
图13

图14

分析第①小题应尽可能让学生得分，入口要宽，设置的问题“当m=0时，求△OPH的面积”.一方面，当m=0时，直线l过原点，使问题背景更简洁，在对问题的理解上作了铺垫;另一方面，求△OPH的面积时，需要用到PH与抛物线对称轴夹角45°这一结论，这为第②题的求解起到引领思路的作用，从而降低求解难度.

第②题的求解，对2种等腰直角三角形的2种情况(如图15)，只要能够分析画出图形，求出点P的坐标，是容易的.对后2种的求解则需要有一定的综合分析能力.

如图13，点P在边BC上，则点P为∠OGD的角平分线与BC的交点，有GE=GF，设为t.

方法1如图15，过点F分别作FH⊥PE于点H，FK⊥x轴于点K，则△PHF，△FGK为等腰直角三角形，从而

由PE=PH+EH，得

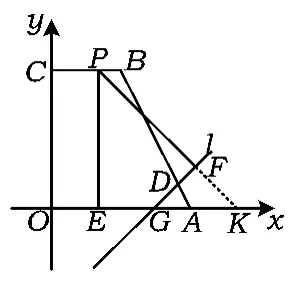
图16

图17

方法4如图18，过点F构造矩形PQKE，则

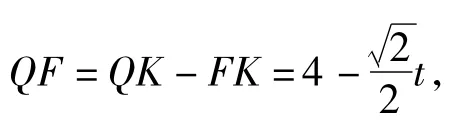
由QF=PQ，得

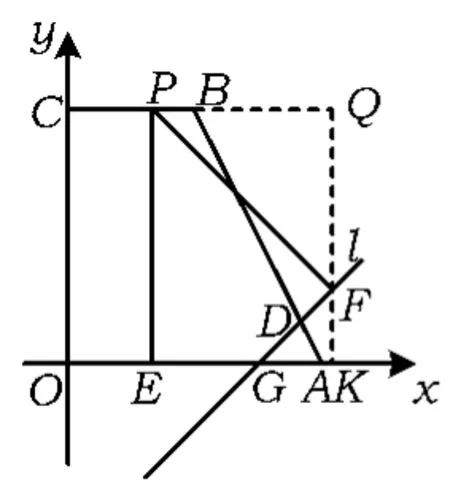
图18

图19

图20

方法5如图19，分别过点E，G作直线l，PF的平行线，相交于点H，则

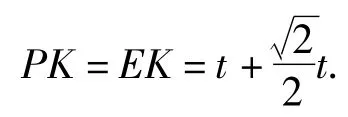
方法6如图19，过点E作EK⊥PF于点K，GH⊥EK于点H，则

方法7如图20，延长FP交y轴于点K，设CP=m，则△KFH是等腰直角三角形.由，得

方法8如图21，延长CP交直线l于点K，设CP=m，则△KCH，△PFK是等腰直角三角形.由CH=CK，得

图21

4 命题反思

4.1 选择教材素材，引导教学导向

教材是课程标准的载体，是课程目标和课程内容的具体化，以教材中的核心概念、性质法则和例题习题为载体，将有效地检测学生对知识的理解与掌握程度，而背景“亲切熟悉”，可以确保情境的公平性，将有利于学生的发挥.选择一个核心的教材内容，加工改造，将解决问题需要的数学思想方法和数学文化内隐其中，就可以创造出一个崭新的试题.

角平分线定理、等腰三角形等问题都是学生熟悉的，顶点P在梯形边上运动，很自然地将角平分线定理的基本图形内隐其中，但夹角为45°角的不变性，为图形的分析给出思路和求解方向.既保证了情境的公平性，尊重了学生认知水平的差异，又对引导课堂教学回归教材，师生重视教材、用好教材，对减轻学生课业负担、减少题海战术有一定的现实意义，对教学有着积极的导向作用.

4.2 问题引导探究，感悟数学思想

依托课本素材进行命题，反应数学的本质.本题是等腰三角形存在性探究问题，难于用两点距离公式进行求解，引导学生画出图形，根据图形的特征寻求解题思路.

问题的设置，基于对学生知识水平和活动经验积累的了解;问题的呈现，采用递进式的循序渐进.第1)小题入口窄，对最后一问的求解提供思路或知识的铺垫;第2)小题的解决，对等腰直角三角形2种情况，求解通过画图是不难发现其结果的，但角平分线上2个点的求解，涉及不同的数学思想方法，增加图形分析的转化层次，增加题目分析过程的复杂性，需要学生较高的思维能力，比较丰富的数学积累，来表现出自己在从事观察、数学表达、猜想、推理等数学活动方面的能力，在问题的探究解决过程中，能很好地甄别学生的数学素养.

4.3 解题思路多元，突出考查思维

试题的设计应突出数学思想方法的应用价值，增加思维量而适当控制计算量.如图13，当点P为直线l与x轴夹角的角平分线与梯形的边的交点时，图16～19所示的方法都是根据“∠EPF=45°”这一图形特征，用不同的形式补成等腰直角三角形.图18中补成一个矩形，出现2个等腰直角三角形;图19中则分割成1个矩形和2个等腰直角三角形;而图15中则补成直角梯形，再利用直角梯形的特征分割成矩形和一个等腰直角三角形.通过割补这2种常见手段，出现等腰直角三角形，转化为方程问题得到解决.