NCCR方程在近平衡气体流动区域的验证

肖 洪,师羊羊,商雨禾,刘振侠

(西北工业大学动力与能源学院，西安710072)

NCCR方程在近平衡气体流动区域的验证

肖 洪,师羊羊,商雨禾,刘振侠

(西北工业大学动力与能源学院，西安710072)

不同于Grad矩方法(R13方程)和Chapman-Enskog展开(Burnett方程)，Eu方法考虑H定理和熵增，由Boltzmann方程导出了气体动力学守恒方程的高阶量本构方程，暨NCCR方程，其在二维高Kn数稀薄气体领域得到了验证。首先呈现了NCCR与Grad矩方法和Burnett方程的区别，而后展示了由Boltzmann方程到守恒方程和NCCR本构方程暨建立联系稀薄统一算法的过程。解决NCCR方程强非线性难题，扩展了间断伽辽金求解NCCR和守恒方程的数值方法，耦合了Langmuir边界条件，并在近平衡区域对典型圆柱绕流、三维高超构型流场进行了数值计算和验证。验证结果表明，在近平衡区域NCCR准确捕捉到了流场信息，包括滞止线参数分布等；同时，NCCR模型在高超构型的后体区域，相比于NS方程更吻合于实验结果。研究为NCCR方程在三维领域的完善和在高Kn数稀薄流动区域的进一步验证提供了基础。

NCCR；非牛顿粘性应力理论；非傅里叶热传导理论；高超声速稀薄流动

1 引言

连续、动量、能量三大守恒方程耦合牛顿粘性定律和傅里叶热传导定律，我们称为纳维-斯托克斯-傅里叶方程(NSF方程)，其在过去近两百多年里推动了流体力学的发展，取得了巨大成功。但是随着新的工程问题出现(特别是解决航天器返回大气层、临近空间飞行器空气动力学等重大工程问题)和流体力学的进一步发展，基于连续介质(或者平衡态)的NSF方程在稀薄气体和非平衡态领域的劣势逐渐显现出来[1]。为了研究稀薄领域的流动现象，在过去近半个世纪，人们先后从两大方向做了大量工作:

1)从研究微观粒子运动或分布函数输运方程方向，发展了 DSMC[2，3]、DSMC-IP[4，5]、直接求解 Boltzmann方程[6]、BGK-Boltzmann方程[7]、LBM[8]等系列方法，特别是以G.A.Bird为代表的DSMC方法在稀薄气体领域取得了成功，直接推动了稀薄气体动力学的发展。同时为了处理连续稀薄耦合流动问题，人们在 NS/DSMC耦合算法[9]、统一Boltzmann方法[10]方面也开展了卓有成效的工作。我国学者沈青、樊箐、孙泉华和美国学者 Boyd[4，5]等在 DSMC的基础上，发展的DSMC-IP方法，将DSMC扩展至低速领域；同时李志辉在统一跨流域Boltzmann方法[10]领域做出了重要贡献。需要特别指出的是徐昆教授提出的UGKS[12]把时间和空间尺度看成动力学量，发展了更为基础的直接建模方法和分布函数方程，做出了杰出贡献。

2)从流动守恒方程和本构关系方向发展了Grad矩方法[13]、以Chapman-Enskog展开为基础的Burnett方程[14]、Eu方法及NCCR理论[15，16]。目前，人们一般认为Boltzmann方程是全流域气体动力学控制方程，在分布函数(分子几率函数)输运过程中，由于存在碰撞不变量，因此同样可以导出连续、动量和能量三大气体动力学守恒方程。为了封闭守恒方程中的粘性应力、热传导等高阶量，NSF方程采用了最简单的线性牛顿粘性定律和傅里叶热传导定律。基于同样的思维，既然连续、动量、能量的守恒方程可以通过Boltzmann方程导出，人们认为粘性应力、热传导等非守恒量的本构方程也同样可以基于Boltzmann方程导出，这就是所谓的模型化Boltzmann方法。在20世纪，以Grad(1949)提出的矩方法[13](以此为基础的R-13方程[17])和以Chapman-Enskog展开为基础的Burnett方程[14](1936)是这类方法的代表。但是部分研究发现，该两类方法不满足热力学定律的熵条件，也就不满足Boltzmann方程的定解条件H定理，可能会限制该类方法的发展[18-20]。

20世纪 90年代，化学专业出身的 B.C.Eu[15]对不可逆热力学学过程进行了研究，对Boltzmann方程进行了模型化处理。Eu处理过程不同于Grad矩方法和Chapmann-Enskog展开，其特点是:①从Boltzmann方程的定解条件H定理出发，抓住了从非平衡态到平衡态熵增的特点，构造的分布函数只是一种分布函数的形态定义而不是严格的具体表达式；②根据熵增耗散的物理概念构建了非平衡态到平衡态的熵增耗散数学模型，其在趋近平衡态时熵增数学模型收敛为Rayleigh-Onsager耗散函数；以此为基础建立了非平衡态到平衡态统一的非线性熵增模型，进而处理了Boltzmann方程的碰撞项。

依据上述原则，Eu从Boltzmann方程导出了粘性应力、热传导等高阶量的输运方程暨本构方程，耦合同样由Boltzmann方程导出的守恒方程，完成了气体动力学方程的封闭。随后Eu和Myong对本构方程做了不同的处理方法，Eu重点处理了本构方程的扩散项；而Myong重点处理了本构方程高阶项并以此为基础构建了非线性耦合本构关系暨NCCR方程[16]。

由于NCCR方程的强非线性关系，传统的有限体积法求解流动守恒方程和NCCR模型受到限制，为解决这一困难，本文继续发展了混合模态间断伽辽金算法(Mixed Modal DG)的NCCR求解体系，作为验证的第一步本文首先在近平衡区域对典型圆柱绕流、三维高超构型流场进行了数值计算和验证，为下一步NCCR的完善和在高Kn数三维稀薄流动区域的验证奠定了基础。

2 NCCR方程及其与Grad矩方法、Burnett方程的区别

2.1 NCCR方程

在没有外场力的假设前提下，包含惯性矩I和角动量j的双原子分子 Boltzmann动力学方程[15]如式(1):

其中f，v，r，ψ，j，I，R[f]分别表示粒子分布函数，粒子速度，位置，与分子方向相关的方位角，角动量向量j的标量，惯性矩标量和碰撞积分。通过f，v，r等微观量定义质量、动量、能量等守恒变量和非守恒变量应力、热传导，并代入Boltzmann动力学方程，无量纲化后可得到流体动力学守恒方程[15，16]式(2)。

式中，U为守恒变量，Finv(U)为无粘项，Fvis(U)为粘性项，Π为粘性应力，Q为热传导，fb为附加应力相对粘性系数(对于单原子气体为0)，I为单位张量。

其中Ec是马赫数Ma的函数。

非守恒变量粘性应力、热传导等在时间上微分耦合 Boltzmann方程，由此得到非守恒变量Φ(k)的输运方程[16]如式(3):

其中ψ(k)为Φ(k)的通量，Λk为分子碰撞耗散项，Zk为分子扩散引起流体流线效应的动能项。

根据Eu和Myong的假设，解析后非守恒变量输运方程[15-16]如式(4):

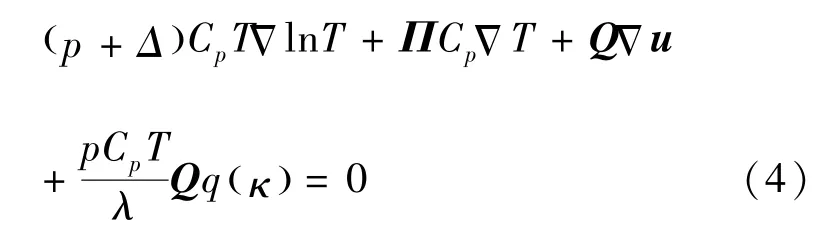
式中，q(κ)＝sinhκ/κ，κ2为Rayleigh-Onsager耗散函数，γ′＝(5－3γ)/2(γ为比热比)，ηb为附加应力粘性系数，Cp为定压比热。

进一步将输运方程(4)无量纲化，可得式(5):

此即为NCCR模型。式中c分子模型参数，R为无量纲Rayleigh-Onsager耗散函数，Π0为牛顿粘性应力，Δ0为线性附加正应力，Q0为傅里叶热传导。NCCR模型(5)和流动守恒方程(2)耦合组成了NCCR的基本理论体系。

如果不考虑附加体积正应力，即 fb＝0，Δ＝0。并继续对NCCR模型(5)继续演化[16]可得式(6):

上式中，Π0，Q0分别为牛顿粘性应力和傅里叶热传导；Πi，Qi可以看做各高阶量。Nδ为复合系数，是马赫数和努森数的函数:

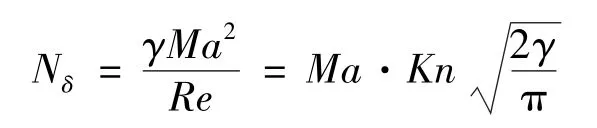
我们遇到的大多数问题，属于低马赫数和小努森数的问题，即Nδ取值很小，此时(6)式中的各高阶量可以忽略，变为式(7):

同时由于在Stokes假设中不考虑附加体积正应力，即fb＝0，Δ＝0，流动守恒方程(2)变为式(8):

方程(7－8)即为NS方程。上述的演化，我们可以得到如下结论，NCCR理论并没有推翻NS方程，只不过NS方程是NCCR理论在平衡态附近或者连续区域的演化特例而已，这一点从公式(6)可以看出。

2.2 NCCR方程与Grad矩方法、Burnett方程的区别

为了对比的需要，图1给出了Grad矩方法、二阶Burnett方程、三阶Burnett方程和NCCR的一维无量纲正应力对比图(具体见文献[21]图2和文献[22]图1)，可以看出:

图1 无量纲一维NCCR正应力对比图［21，22］Fig.1 The comparisons of normal viscous stress in NCCR，Grad，Burnett and NS［21，22］

1)NCCR、Burnett和Grad矩方法在平衡态附近均和牛顿粘性定律呈现一致的线性关系，且在近平衡区域三者非线性关系吻合；后两者均能处理近平衡区域问题，因此从这个角度基本可以判断NCCR在近平衡区域的应用是可信的。

2)NCCR在远离平衡态区域呈现出与Burnett方程和Grad矩方法不同的非线性趋势。需要指出的是Burnett方程和Grad矩方法均不能处理远离平衡态气体流动，因此该趋势也为NCCR处理远离平衡态区域的气体流动提供了可能性，且已经执行的二维研究结果表明NCCR在远离平衡态区域取得了和DSMC、UGKS等一致的结果[23-25]。

3 间断伽辽金求解NCCR方程

如公式(2)所示，对于流动守恒方程，定义附加参数S的系列方程组如式(9)，可见粘性应力等高阶量是S的函数[16-18]。

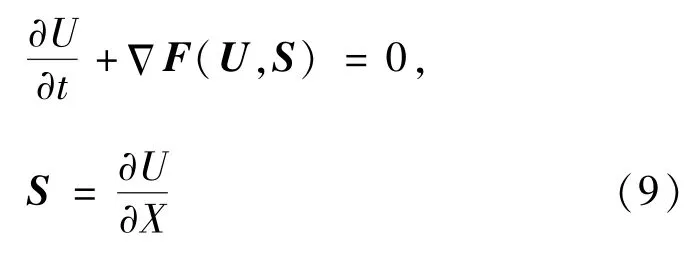
在每个网格内，守恒变量U和附加参数S近似为式(10):

N的取值取决于精度。

方程(9)对网格积分得式(11):

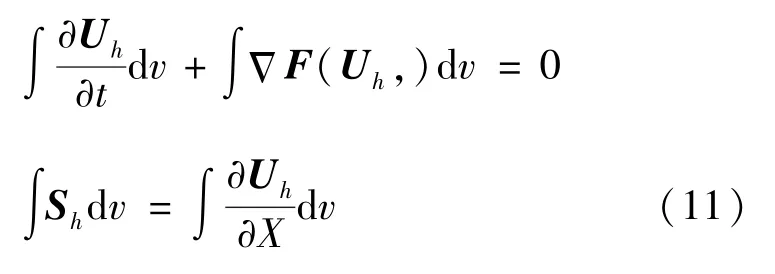
为检验(10)近似的精度，选取检验函数带入(11)式，在间断伽辽金算法中，检验函数也是基函数，带入得式(12):

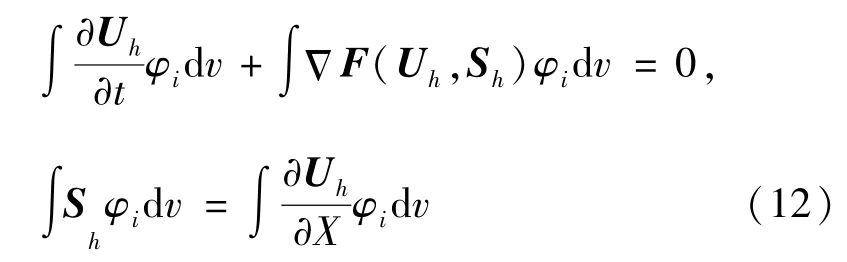
在方程(12)中，每一步迭代可以得到附加参数S近似表达式Sh的系数bi，进一步得到NCCR模型(5)中的Π0Q0。以此为基础，进一步通过(5)式迭代NCCR的粘性应力和热传导ΠΔQ，代入守恒方程[23]，迭代守恒变量U的近似表达式守恒变量Uh的系数ai，具体过程参见文献[23]。

在稀薄流动中，壁面速度滑移和温度跳跃是较为关键的步骤，本文采用 Langmuir边界条件[19]。

4 算例验证

为验证混合模态间断伽辽金算法求解NCCR理论体系的有效性，本文以现有数据为基础，分别选取高超声速圆柱绕流和三维高超构型对NCCR理论体系进行验证。

4.1 高超声速圆柱绕流

本算例为高超声速算例，工质为氩气，氩气为单原子气体故体积附加正应力为零。计算域外边界为圆形，半径为圆柱半径的20倍；采用三角形网格，壁面网格和径向方向数目分别为100和100。算例计算条件分别如下:Ma＝5.48，Kn＝0.05，T∞＝26.6 K，TW＝293 K；Ma＝20.00，Kn＝1.0，T∞＝TW＝26.6 K。

图2给出了计算网格图，图3给出Ma＝5.48、Kn＝0.05算例圆柱中心前滞止线的速度曲线，可以看出NCCR相比于NS方程更吻合于DSMC数据。

图4给出了极高马赫数算例Ma＝20圆柱表面热流分布的DSMC结果、徐昆教授的UGKS结果和NCCR结果。可以看出在热流的计算中，NCCR同样表现出了优势，其与UGKS结果在整体趋势上极为吻合。

图2 计算网格图Fig.2 Unstructured triangular mesh for the cylinder case

图3 滞止线无量纲速度分布曲线Fig.3 Non-dimension velocity in stagnation line at Ma＝5.48，Kn＝0.05.

4.2 三维高超声速构型实验验证

本算例为三维高超声速算例，构型如图5所示。工质为空气。计算域外边界为圆形，半径为构型长度的20倍；采用四面体网格。三算例计算条件如下(其中Re特征长度取为1米):

图4 圆柱表面热流分布曲线Ma＝20，Kn＝1.0［23］Fig.4 Normalized heat flux at solid surface of high mach number gas flow around a cylinder at Ma＝20，Kn＝1.0［23］

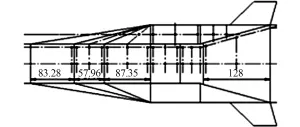
图5 三维构型图Fig.5 3D vehicle configuration

(1)Ma＝7.0，Re＝5.3×105/m，零迎角

(2)Ma＝6.0，Re＝4.2×105/m，零迎角

(3)Ma＝6.0，Re＝4.2×105/m，4°迎角

图6－8分别给出了上述三算例的压力分布计算结果和实验结果。可以看出，前体区域NCCR、NSF结果和实验结果均吻合良好；但是在后体区域NS方程结果的预测均比实验结果低，而NCCR预测结果与实验结果吻合良好，同时该结果对于后续湍流的研究具有启示意义。

图6 Ma＝7.0，Re＝5.3×105/m压力分布Fig.6 The pressure coefficient，Cp，at Ma＝7.0 and Re＝5.3×105

5 结论

Eu方法NCCR方程不同于Grad矩方法和Bunrett方程，其在模型化Boltzmann过程中考虑了H定理和熵增模型。为解决NCCR模型强非线性难题，本文发展了间断模态伽辽金求解NCCR和流动守恒方程的数值算法。并在近平衡区域对典型圆柱绕流、三维高超构型流场进行了数值计算和验证。验证结果表明，验证结果表明，在近平衡区域NCCR准确捕捉到了流场信息。同时验证表明NCCR模型在高超构型的后体区域，相比于NS方程更吻合于实验结果。

图7 Ma＝6.0，Re＝4.2×105/m压力分布Fig.7 The pressure coefficient，Cp，at Ma＝6.0 and Re＝4.2×105

图8 Ma＝4.0，Re＝4.2×105/m 4°迎角压力分布Fig.8 The pressure coefficient，Cp，at Ma＝6.0，Re＝4.2×105and α＝40

NCCR方程作为一种新的气体动理学理论体系，虽然在二维高Kn数区域得到验证，但仍旧需要经过实践检验，不排除其理论推导存在缺陷甚至致命性错误的可能。就本文开展的DG-NCCR工作而言，作者认为其局限性和未来工作在于:

1)相对于NS方程计算时间资源较大，一般NCCR相当于NS方程计算资源的2～4倍。在实际计算中，我们一般采用先计算NS方程，收敛后以此为初值计算NCCR，其时间资源仍旧为NS方程的1.5～2倍。

2)对粘性应力、热传导等高阶量的本构方程处理，Eu和Myong的处理方式不同，前者封闭了通量项但是简化了碰撞项，后者(包括申请者前期工作)封闭了碰撞项但是简化消去了通量项。上述封闭方法和简化对气体动力学特别是对于三维高Kn数流动影响的研究和验证是空白领域。

3)Myong和本文的工作，是成功将Mixed-DG引入NCCR计算理论体系，但是对三维问题特别是上述封闭方法的不同引起的计算解耦方法不同，是空白领域，也需要重新发展。

4)目前NCCR理论没有考虑化学反应，如考虑化学反应需要重新推导。

5)本文的工作为后续三维高Kn数区域流动的验证提供了基础，同时对后续研究湍流问题也具有很强的启示意义。

致谢:感谢韩国庆尚国立大学R.S.Myong教授的公式检查工作和孙泉华研究员的DSMC数据支持，同时感谢香港科技大学徐昆教授的UGKS数据支持。和美国圣地亚哥州立大学 Arnab.Chaudhuri博士多次在壁面处理上的开展讨论，在此表示感谢。

同时特别感谢CFD领域的前辈Roe格式提出者密歇根大学Phil.Roe教授在通量计算上的多次指点和帮助。

（

）

[1]Hadjiconstantinou N G.The limits of Navier-Stokes theory and kinetic extensions for describing small-scale gaseous hydrodynamics[J].Physics of Fluids(1994-present)，2006，18(11):111301.

[2]Bird G A.Molecular Gas Dynamics and the Direct Simulation of Gas Flows[M].Claredon:Oxford，1994:115-123.

[3]Bird G A The DSMC Method[M].Version 1.1.Claredon: Oxford，2013:101-136.

[4]Fan J，Boyd I D，Cai C P，et al.Computation of rarefied gas flows around a NACA 0012 airfoil[J].AIAA journal，2001，39(4):618-625.

[5]Sun Q，Boyd I D.Flat-plate aerodynamics at very low Reynolds number[J].Journal of Fluid Mechanics，2004，502: 199-206.

[6]Frezzotti A，Ghiroldi G P，Gibelli L.Solving the Boltzmann equation on GPUs[J].Computer Physics Communications，2011，182(12):2445-2453.

[7]Bellouquid A，Calvo J，Nieto J，et al.On the relativistic BGK-Boltzmann model:asymptotics and hydrodynamics[J].Journal of Statistical Physics，2012，149(2):284-316.

[8]Nabovati A，Sellan D P，Amon C H.On the lattice Boltzmann method for phonon transport[J].Journal of Computational Physics，2011，230(15):5864-5876.

[9]Wu J S，Lian Y Y，Cheng G，et al.Development and verification of a coupled DSMC-NS scheme using unstructured mesh [J].Journal of Computational Physics，2006，219(2):579-607.

[10]Li Z H，Zhang H X.Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J].Journal of Computational Physics，2004，193(2):708-738.

[11]He X，Chen S，Zhang R.A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh-Taylor instability[J].Journal of Computational Physics，1999，152(2):642-663.

[12]Liu S，Yu P，Xu K，et al.Unified gas-kinetic scheme for diatomic molecular simulations in all flow regimes[J].Journal of Computational Physics，2014，259:96-113.

[13]Grad H.On the kinetic theory of rarefied gases[J].Communications on pure and applied mathematics，1949，2(4): 331-407.

[14]Burnett D.The distribution of molecular velocities and the mean motion in a non-uniform gas[J].Proceedings of the London Mathematical Society，1936，2(1):382-435.

[15]Eu B C.Kinetic Theory and Irreversible Thermodynamics [M].Candana:Wiley，1992.

[16]Myong R S.A generalized hydrodynamic computational model for rarefied and microscale diatomic gas flows[J].Journal of Computational Physics，2004，195(2):655-676.

[17]Torrilhon M，Struchtrup H.Boundary conditions for regularized 13-moment-equations for micro-channel-flows[J].Journal of Computational Physics，2008，227(3):1982-2011.

[18]Torrilhon M.Special issues on moment methods in kinetic gas theory[J].Continuum Mechanics and Thermodynamics，2009，21(5):341-343.

[19]Comeaux K A，Chapman D R，MacCormack R W.An analysis of the Burnett equations based on the second law of thermodynamics[C]//AIAA，Aerospace Sciences Meeting and Exhibit，33 rd，Reno，NV.1995.

[20]Balakrishnan R，Agarwal R K，Yun K Y.Higher-order distribution functions，BGK-Burnett equations and Boltzmann′s H-theorem[R].AIAA-1997-2551，1997.

[21]Myong R S.Thermodynamically consistent hydrodynamic computational models for high-Knudsen-number gas flows[J].Physics of Fluids，1999，11(9):2788-2802.

[22]Myong R S.On the high Mach number shock structure singularity caused by overreach of Maxwellian molecules[J].Physics of Fluids，2014，26(5):056102.

[23]肖洪，商雨禾，吴迪，等.稀薄气体动动力学的NCCR理论及其验证[J/OL].航空学报，2014，35.http://hkxb.buaa.edu.cn/CN/article/downloadArticleFile.do？attachT-ype＝PDF＆id＝15759.Xiao H，Shang Y H，Wu D，et al.Nonlinear coupled constitutive relations and its validation for rarefied gas flows[J].Acta Aeronautica et Astronautica Sinica，2014，35.http://hkxb.buaa.edu.cn/CN/article/downloadArticleFile.do？attachT-ype＝PDF＆id＝15759.(in Chinese)

[24]Le N T P，Xiao H，Myong R S.A triangular discontinuous Galerkin method for non-Newtonian implicit constitutive models of rarefied and microscale gases[J].Journal of Computational Physics，2014，273:160-184.

[25]Xiao H，Myong R S.Computational simulations of microscale shock-vortex interaction using a mixed discontinuous Galerkin method[J].Computers＆Fluids，2014，105:179-193.

Validation of Nonlinear Coupled Constitutive Relations in Near-equilibrium Gas Flows

XIAO Hong，SHI Yangyang，SHANG Yuhe，LIU Zhenxia
(School of Power and Energy，Northwestern Polytechnical University，Xi′an 710072，China)

Different from Grad moment method(R-13 equations)and Chapman-Enskog method (Burnett equation)，the Nonlinear Coupled Constitutive Relations(NCCR)of high order terms including viscous stress and heat flux were derived from Boltzmann equation in B.C.Eu method by considering the H theorem and entropy generation.And it was validated in the two dimensional rarefied gas flow.Firstly，the difference between Grad moment method，Burnett equation and NCCR were presented.Conservations laws and transport equations of non-conservation variables were derived from Boltzmann equation and then a unified scheme of continuum-rarefied gas flows，named by nonlinear coupled constitutive relations(NCCR)，was proposed.For solving the conservation laws with NCCR model，a modal mixed discontinuous Galerkin(DG)method with Langmuir slip condition，was developed based on unstructured grids.To validate the present DG-NCCR method，hypersonic rarefied gas flow over a cylinder and 3D hypersonic configuration，were considered by NCCR.It is observed that，compared with DSMC results，DG-NCCR could capture shockwave which is better than NSF.Investigations also showed that the DG-NCCR results were close with DSMC data than the NSF results in velocity at stagnation line.Furthermore，NCCR results were found to be in good agreement with experiment in pressure distribution of the gas flow in the afterbody of 3D hypersonic configuration.The present study provided a foundation for the improvement of NCCR and its validation in 3D high Kn number gas flows.

NCCR；non Newton viscous stress；non Fourier heat flux；hypersonic rarefied gas flows

O356

A

1674-5825(2015)03-0303-06

2014-08-13；

2015-03-11

韩国国家自然科学基金(NRF 2012-R1A2A2A02-046270)

肖洪(1978－)，男，博士，副教授，研究方向为连续稀薄统一气体动力学方程。E-mail:xhong＠nwpu.edu.cn