迭代制导在月面上升段的应用研究

巩庆海,宋征宇,吕新广

(北京航天自动控制研究所，北京100854)

迭代制导在月面上升段的应用研究

巩庆海,宋征宇∗,吕新广

(北京航天自动控制研究所，北京100854)

针对迭代制导在月面上升段的应用开展研究。首先对迭代制导基本原理及其在运载火箭上的应用进行了回顾，给出了月面上升段的动力学模型和迭代制导算法模型。并通过对比应用场景，深入研究了垂直起飞段和迭代制导段的衔接，提出了针对月面上升段特点、兼顾工程可实现性和燃料最优的迭代制导应用方案。对发射点参数、目标轨道参数、迭代初值的获取方式进行了讨论。最后以阿波罗12号飞船载人月面返回的任务场景为算例，进行Monte Carlo模拟打靶数学仿真验证，表明迭代制导在月面上升段具有较高的入轨精度。

迭代制导；月面上升；载人登月；阿波罗飞船；数学仿真

1 引言

迭代制导是一种根据预定目标轨道参数和飞行器实时运动参数进行实时程序角指令计算的制导方法。国外学者对迭代制导主要研究集中于Apollo飞船载人登月前后(20世纪六七十年代)，如Baker C.D.[1]阐述了土星运载火箭的迭代制导律。其后，国内学者如钟锡保、韩祝斋等进行了相关研究和翻译工作[2]。程国采[3]引入等效椭圆轨道，得到简化了的状态方程，在此基础上给出了可适用于大型运载火箭的制导方法，该方法的方程形式与土星运载火箭的迭代制导律形式较为接近。

最近十年以来迭代制导成为国内运载火箭制导控制领域学者的研究热点之一。陈新民、余梦伦[4]基于运载火箭的实际飞行情况，建立了迭代制导的工程计算模型，给出了较为详细的算法表达式，并结合某型运载火箭进行大量的实例计算分析，对迭代制导的制导精度、自适应能力等方面进行研究。周国财[5]利用最优控制理论，建立运载火箭的最优控制泛函，得出了满足卫星轨道终端条件的迭代制导方程，并分析在不同终端条件下，运载火箭迭代制导方法的可行性，有一定的理论意义和工程实用价值。李华滨等通过引入“平均引力”的简化假设，推导了应用于小型固体运载火箭的迭代制导方程，给出了算法实现的流程和仿真结果，可以满足1～5个卫星轨道终端条件[6]。吕新广、宋征宇[7]重点论述了迭代制导在工程应用中的可靠性设计方法，并以载人运载火箭为模型进行了数学仿真，对算法的可靠性、适应性及精度进行了探讨，验证了算法的适应性和良好的制导精度，具有很好的工程应用价值。

宋征宇[8，9]综述了迭代制导的应用情况，可见迭代制导在实际飞行试验中取得了很好的应用效果。吕新广等针对运载火箭入轨多约束需求，提出一种将迭代制导与数值积分相结合的轨迹预测制导方法[10]，能够同时满足终端姿态约束和轨道参数约束要求，并且计算量较小，适合箭上实时计算要求，并通过数学仿真算例分析了该方法的性能。

我国已完成CE-3落月探测，下一步将要实施的采样返回任务中，必然要针对月面上升段制导方法开展研究和验证工作。本文首先简要回顾了迭代制导基本原理和在运载火箭上的研究与应用情况，对比分析了月面上升段与运载火箭上升段的异同，给出了月面上升段迭代制导应用方案，并结合Monte Carlo模拟打靶数学仿真验证，说明了迭代制导方法在月面上升段的应用效果。

2 迭代制导方法原理与应用

2.1 迭代制导基本原理

2.1.1动力学方程

月面上升段无气动力，飞行器动力学方程如式(1)～(3)所示。

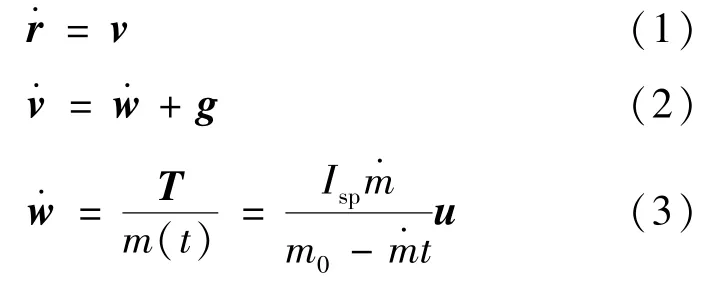
其中，r、v、w、g、u分别为飞行器在轨道坐标系下(坐标系定义可参考文献[4，7])的位置矢量、速度矢量、视速度矢量、引力矢量和单位化控制矢量，m(t)为当前质量，t为飞行时间，Isp为发动机比冲，m0为起飞初始质量，为燃料秒耗量，对于定推力发动机该参数设为定值。

2.1.2 迭代制导指令输出形式

迭代制导指令输出形式如公式(4)－(5)所示:

2.1.3 积分预测过程

求取指令程序角中终端位置约束分量过程中，需要对后续飞行过程的速度、位置分量进行积分预测，采用推力分量和引力分量分别积分的方式实现。其中，引力分量积分过程引入了引力平均假设。

2.1.4 引力平均假设

由于飞行器在剩余飞行时间里每一时刻的引力加速度是位置矢量的函数，而位置矢量本身又通过预测得到，这一过程非常复杂。为了简化问题，引入式(6)所示引力平均假设，即假设未来飞行过程中的引力矢量为当前点引力矢量与目标点引力矢量的均值，随着逐步接近目标点，引力平均假设的真实性和精度也不断提高[7]。

式(6)中，g0为飞行器当前点引力加速度矢量，gk为飞行器入轨点引力加速度矢量。

2.1.5 剩余飞行时间(预测关机时间)Tk的求取

剩余飞行时间是以飞行器当前瞬时为零秒，至飞行器关机入轨所需预估时间。其求取是通过联立公式(7)中待增速度增量与公式(8)中按发动机模型计算的Tk时间内所能提供的速度增量关系得到的，可见该方程组存在超越函数，因此，求解过程需要进行迭代计算。

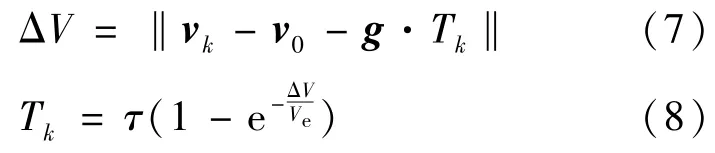
式(8)中，τ为完全燃烧时间，即按当前瞬时秒耗量计算飞行器消耗完全部质量的时间；vk为关机点期望速度矢量，v0为当前速度矢量，Ve为排气速度。

2.2 迭代制导在运载火箭上升段的应用

我国迭代制导首次应用于神舟八号飞船发射任务，在神舟九号发射中也得到了成功应用，实现了高精度入轨[8]。

在迭代制导使用中，为了避开大气影响，从火箭二级飞行段开始采用，接入前采用摄动制导律进行控制，形成摄动＋迭代的接力制导方式。在应用过程中采用了大量的可靠性措施[7]，包括:

1)对可能产生突变的输入信息进行滤波处理，提高迭代算法的平滑性；

2)采用考虑推重比变化和后效过程的多阶段联合迭代；

3)合适的角速度和角度限幅环节。

3 迭代制导在月面上升段的应用

3.1 迭代制导在月面上升段的应用分析

迭代制导算法推导考虑的基本假设条件[2]:

1)应用于真空段，无气动力干扰；

2)引力平均假设；

3)推力大小不变，方向可调。

分析可知，对于月面使用条件，迭代制导算法的基本假设都是成立的，因此，理论上是可用的。

月面上升任务与运载火箭应用场景仍存在一定的差异，例如:不需做从摄动制导转换到迭代制导的制导律切换，但由于起飞段需保持竖直上升，即在垂直段转入迭代制导，因此要着重考虑程序角的平滑过渡问题。

3.2 月面上升段迭代制导方案

3.2.1 迭代制导流程分段

图1 迭代制导应用分段示意图Fig.1 Phases of iterative guidance application

如图1和表1所示，根据程序角的计算和使用可将上升段飞行过程分为四段:

1)垂直上升段:本段内，迭代程序角实时更新，但输出的指令程序角保持为常值，一般以速度或高度大小满足一定条件判断是否进入下一阶段；

2)过渡段:在较短时间内，使指令程序角逐步由垂直程序角切换过渡至迭代程序角；

3)实时迭代段:指令程序角随迭代程序角实时更新，上升段大部分时间处于该阶段；

4)程序角保持段:接近入轨时，指令程序角保持，以避免指令波动。

表1 阶段划分Table 1 Phases of lunar ascent

3.2.2 发射点、目标轨道参数和迭代初值的获取

发射点参数(包括发射点射向、纬度、经度等)获取方式有两种:一种是在着陆前已确定，可行的方式包括着陆过程中地形匹配等方式确定；一种是月面运行过程中通过地面或飞行器载荷设备进行测定轨方式获得。

迭代制导所需的目标轨道根数可以通过推算或射前注入的形式获得。前者是指在着陆前已确定目标轨道模型，在月面运行过程中利用轨道推算形式，推算发射时刻目标轨道参数；后者则需保证测控条件的满足，对于应急起飞状态适应性较差。

另外，迭代初值也需要在起飞前确定，因此，可以考虑在迭代制导初始化前设计一个规划模块，根据收集到的发射点、目标轨道参数、发动机比冲和秒流量等参数设计合理的迭代初值，如剩余飞行时间估计初值、发射方位角等参数[4]。

4 数学仿真验证

4.1 仿真场景

本文以Apollo 12号飞船载人月面上升返回任务场景为算例开展算法验证[11]。

表2、表3和表4分别列出了飞船起飞点初始参数、目标点参数以及仿真计算中所采用的月球物理常数。

表2 初始参数Table 2 Initial parameters

表3 目标轨道参数Table 3 Target orbit parameters

表4 月球物理参数Table 4 Lunar physical parameters

仿真计算周期设置为0.02 s，关机计算周期设置为0.002 s。

4.2 垂直上升与迭代制导衔接方式的选择

由月面上升段的阶段划分可知，与运载火箭在飞行中段才接入迭代制导不同，月面上升段迭代制导程序角在起飞后较短时间内就接入并参与控制了。这一差异可能造成初始迭代程序角和垂直段指令程序角间存在较大的初始差异，以本算例为例，这一差异接近50°，即需要通过调整指令程序角，消除这50°的程序角差异，将二者平滑衔接起来。

表5 调姿方式对比Table 5 Comparison of attitude adjustment mode

分析表5中的规律可知:衔接方式及参数选取直接影响衔接过程是否可实现以及入轨燃料消耗。

相同调姿时间内，线性调姿方式消耗燃料小于最优二次曲线调姿方式，但二者差别小于1 kg；两种调姿方式均随调姿时间延长而使燃料消耗增大，增加5 s的调姿时间约对应2～3 kg的燃料消耗。

从角速度和角加速度看，线性调姿方式对应的最大角速度小于最优二次曲线调姿方式，二者关系约为1:2，最大角速度在10°/s左右；而线性调姿方式的角加速度却达到了 87.5～128.3125°/s2，这在实际上是较难实现的，因此，采用最优二次曲线调姿更为合理。根据Apollo飞船力矩提供能力计算，最大2.0625°/s2的角加速度在其可提供的范围之内，且有30%左右余量。

仿真表明在10 s时刻，垂直向上的速度已达到15.6 m/s，与Apollo飞船达到15 m/s即开始转弯的条件是对应的。

因此，本文后续仿真中选择周期为10 s的最优二次曲线调姿方案来衔接垂直上升段和迭代制导段程序角，如图2所示。

4.3 仿真结果与分析

表6中列出了迭代制导所使用到的相关参数设置。其中，俯仰程序角初值和角速率限幅值需结合飞行轨迹和飞行器参数，通过仿真确定。

表6 迭代制导参数设置Table 6 Iterative guidance parameters

由表7可见，零干扰状态下，迭代制导可以实现很高的入轨精度，且5个轨道参数偏差均较小，这与在运载火箭上的应用情况是一致的。偏差状态控制效果的仿真验证及与摄动制导方法的控制效果比较可参考文献[8]。

表7 仿真结果Table 7 Simulation results

由图3－5可知，月面上升飞行过程中指令程序角计算平稳，迭代程序角速率除初始段达到3°/s限幅外，其余各段变化平稳。预估关机时间Tk全程连续平稳变化至程序角保持段。相关入轨参数和程序角曲线说明了迭代制导在月面上升段良好的应用效果。

图3 飞行过程俯仰、偏航程序角Fig.3 The pitch and yaw program angles in flight

图4 飞行过程俯仰、偏航迭代程序角速率Fig.4 The pitch and yaw program angle rates in flight

在零干扰仿真基础上进行了1000组Monte Carlo仿真，干扰和仿真结果分别列于表8和表9中，入轨参数偏差散布如图6所示。从图6可见，干扰正态分布下，入轨偏差散布基本呈正态分布。由表9可知，对应表8的干扰，上升入轨近月点偏差≤70 m，远月点偏差≤120 m，轨道平面偏差≤0.01°，Monte Carlo仿真结果验证了迭代算法对于典型干扰的适应性和精度。

图5 预估关机时间Fig.5 The predicted cutoff time

表8 干扰与偏差Table 8 Disturbances and errors

表9 Monte Carlo仿真结果Table 9 Monte Carlo simulation results

5 结论

本文对比分析了月面上升段与运载火箭上升段的任务场景，讨论了迭代制导在月面上升段应用的可行性，建立了月面上升段的动力学模型和迭代制导算法模型，重点分析并提出了垂直上升段与转弯段的最优衔接方法。提出了针对月面上升段特点、兼顾工程可实现性和燃料最优的迭代制导应用方案，并对发射点参数、目标轨道参数、迭代初值的获取方式进行了讨论。最后以Apollo 12号飞船月面上升段为算例进行了Monte Carlo仿真验证，研究表明:

图6 Monte Carlo模拟打靶散布图Fig.6 Monte Carlo simulation distributes

1)所提出迭代制导应用方案适用于月面上升段的制导控制，并具有较高的入轨精度；

2)考虑月面上升段与运载火箭上升段的任务场景差异，需要结合具体任务开展迭代制导方案和制导参数的针对性细化设计。

（

）

[1]Baker C D.Concepts of the Iterative Guidance Law for Saturn Launch Vehicles[R].NASA-TM-X-53389，1965.

[2]韩祝斋.用于大型运载火箭的迭代制导方法[J].宇航学报，1983，4(1):9-21.Han Zhuzhai.An Iterative Guidance Method for the Large Launch Vehicle[J].Journal of Astronautics，1983，4(1): 9-21.(in Chinese)

[3]程国采.运载火箭显式制导方法研究[J].航天控制，1988，6(3):1-9.Cheng Guocai.Stduy on Explicit Guidance Method[J].Aerospace Control.1988，6(3):1-9.(in Chinese)[4]陈新民，余梦伦.迭代制导在运载火箭上的应用研究[J].宇航学报，2003，24(5):484-501.Chen Xinmin，Yu Menglun.Study of iterative guidance application to launch vehicles[J].Journal of Astronautics，2003，24(5):484-501.(in Chinese)

[5]周国财.运载火箭迭代制导方法研究[D].西安:西北工业大学，2003.Zhou Guocai.Research on Iterative Guidance Method of Launch Vehicle[D].Xi’an:Northwestern Polytechnic University，2003.(in Chinese)

[6]李华滨，李伶.小型固体运载火箭迭代制导方法研究[J].航天控制，2002，20(2):29-37.Li Huabin，Li Ling.Iterative Explicit Guidance for Small Solid Launch Vehicle[J].Aerospace Control，2002，20(2): 29-37.(in Chinese)

[7]吕新广，宋征宇.载人运载火箭迭代制导方法应用研究[J].载人航天，2009，15(1):9-14.Lv Xinguang，Song Zhengyu.Study of Iterative Guidance Engineering Application to Manned Launch Vehicle[J].Manned Spaceflight，2009，15(1):9-14.(in Chinese)

[8]宋征宇.从准确、精确到精益求精—载人航天推动运载火箭制导方法的发展[J].航天控制，2013，31(1):4-10.Song Zhengyu.From Accurate，Precise to Perfect—Manned Space Promotes the Development of Guidance Method on Launch Vehicle[J].Aerospace Control，2013，31(1):4-10.(in Chinese)

[9]宋征宇.采用敏捷发射和自由飞行技术提升运载火箭竞争力[J].航天控制，2013，31(6):3-9.Song Zhengyu.Smart Launch，Free Fly—The Effect of Control System on Elevating Competitiveness of Launch Vehicle [J].Aerospace Control，2013，31(6):3-9.(in Chinese)

[10]吕新广，宋征宇，巩庆海.运载火箭轨迹预测制导方法研究[J].载人航天，2013，19(6):20-24.Lv Xinguang，Song Zhengyu，Gong Qinghai.Research on Trajectory Prediction Guidance for Launch Vehicle[J].Manned Spaceflight，2013，19(6):20-24.(in Chinese)

[11]Nolley J.W.Apollo 12(mission H-1)spacecraft dispersion analysis.Volume 7:Dispersion summary[R].NASA-TM-X-72099，1969.

Study on Application of Iterative Guidance in Lunar Ascent

GONG Qinghai，SONG Zhengyu∗，LV Xinguang
(Beijing Aerospace Automatic Control Institute，Beijing 100854，China)

The application of iterative guidance in lunar ascent was studied.Firstly，the foundation of iterative guidance and its application in launch vehicle were reviewed，then the dynamic model and iterative guidance algorithm were proposed.By comparing the differences between the two scenes and considering the lunar characteristic，the application scheme of iterative guidance in lunar ascent，with the advantage of both engineering obtainable and fuel optimal，was proposed.The link up of the vertical ascent phase and iterative guidance phase was thoroughly studied.The way of acquiring initial launch point parameters，target orbital parameters and initial parameters of iterative guidance for lunar ascent was discussed.Finally，the iterative guidance was tested by Monte Carlo simulation under the scene of Apollo 12 manned spacecraft returning from lunar surface，which demonstrated a high insert precision.

iterative guidance；lunar ascent；manned lunar landing；Apollo spacecraft；mathematical simulation

V44

A

1674-5825(2015)03-0231-06

2014-09-11；

2015-04-11

载人航天预先研究项目(020301)

巩庆海(1980－)，男，硕士，高级工程师，研究方向为运载火箭制导系统设计。E-mail:gqh_calt12＠126.com

∗通讯作者:宋征宇(1970－)，男，硕士，研究员，研究方向为运载火箭控制系统。E-mail:zycalt12＠sina.com