水平井定面射孔条件下水力裂缝起裂机理

刘合，兰中孝，王素玲，许建国，赵晨旭

（1.中国石油勘探开发研究院；2.大庆油田有限责任公司；3.东北石油大学机械科学与工程学院；4.中国石油吉林油田采油工程研究院）

水平井定面射孔条件下水力裂缝起裂机理

刘合1，兰中孝2，王素玲3，许建国4，赵晨旭4

（1.中国石油勘探开发研究院；2.大庆油田有限责任公司；3.东北石油大学机械科学与工程学院；4.中国石油吉林油田采油工程研究院）

建立水平井定面射孔局部地应力计算模型，利用建立的模型分析水平井定面射孔条件下水力裂缝起裂机理，研究井筒位置、射孔参数等对起裂压力的影响规律。根据渗流力学理论建立了定面射孔岩体三维流固耦合地应力模型，采用最大拉应力理论给出了定面射孔起裂压力确定方法，并通过应用实例验证了模型的可靠性。采用模型进行计算分析后发现：对于正断层型和逆断层型地应力场，定面射孔时裂缝均在射孔壁面上起裂，正断层型地应力场易形成宽而短的垂直缝，逆断层型地应力场易形成长而窄的转向缝；对于正断层型地应力场，井筒方位角和井筒倾斜角越大，定面射孔的起裂压力越低；对于逆断层型地应力场，井筒方位角越大、井筒倾斜角越小，定面射孔起裂压力越低；射孔夹角越小、射孔直径越大、射孔深度越大，定面射孔起裂压力越低。图17参15

定面射孔；水力压裂；体积压裂；裂缝起裂机理；裂缝起裂压力

0 引言

水平井体积压裂是致密储集层及页岩储集层增产的主要措施[1-4]，目的是通过水力压裂增加水力裂缝在井筒周围的扩散体积。目前常用的螺旋射孔与定向射孔技术，水力压裂后可形成沿最大主应力方向扩展的单一主裂缝[5]，起裂压力高且裂缝较长，裂缝方向不易控制，在分段体积压裂中容易造成段与段间的水力裂缝在隔层位置串通，降低压裂效果，无法达到改善井筒周围储集层渗透能力的目的[6]。因此，针对水平井体积压裂提出了定面射孔新技术[7]。定面射孔技术采用超大孔径射孔弹及特殊布弹方式，射孔后，在垂直于套管轴向同一横截面的内壁圆周上形成多个射孔眼，通过孔眼间的相互作用贯通，降低地层破裂压力，同时在射孔平面内形成较大波及面的人工裂缝，实现近井筒地带裂缝方向可控，提高储集层与井筒的沟通能力，从而提高产能。

国内外学者对螺旋射孔及定向射孔下地层的起裂

压力进行了研究[8-10]，研究时均采用无任何干扰的原始地应力场。然而，井眼和射孔孔眼双重作用导致近井筒地带应力变化较大，特别是定面射孔条件下多个孔眼在1个平面内分布，孔眼间的相互作用使得近井筒地带应力场异常复杂，裂缝起裂与扩展预测困难。因此，螺旋射孔及定向射孔条件下裂缝起裂压力及裂缝扩展形态的研究结果无法用于指导定面射孔工艺。而国内外对定面射孔的起裂机理研究较少，目前无相关文献报道。

本文采用数值模拟技术建立水平井定面射孔局部地应力模型，考虑钻井、固井、射孔等工艺对近井筒地带地应力的累积影响[11-12]，研究定面射孔近井筒地带的地应力分布状态，分析水平井定面射孔条件下水力裂缝起裂机理，探讨井筒位置、定面射孔参数等对起裂压力的影响规律。

1 定面射孔局部地应力模型

1.1 水力压裂作用下储集层流固耦合分析

水力压裂是压裂液流动与岩体变形动态耦合的过程，本文借助Abaqus 6.14-1软件模拟近井筒地层由钻井到压裂的改造过程，模拟通过耦合求解岩体的应力平衡方程和流体连续性方程实现。

在地层岩石的力学分析中，采用拉格朗日格式描述岩体变形，在引入有效应力的基础上根据欧拉-柯西应力原理建立岩体的应力平衡方程：

在对多孔介质进行数值分析时，将固体划分为有限元网格，流体流过此网格。压裂液在1个时间增量内的质量变化可利用连续性方程描述，引入渗流基本定律，可得流体质量连续性方程：

对（2）式采用有限元格式进行离散及拼装组成，再将其与（1）式联立求解，可得到孔隙介质节点的有效应力、应变及孔隙压力等[13-15]。

1.2 定面射孔局部地应力计算模型

为了更加准确地模拟射孔孔眼的应力状态，在考虑套管作用的条件下，建立了水平井定面射孔条件下水力压裂的局部地应力计算模型（几何模型见图1）。为了克服边界的影响及尺寸效应，经反复试算，确定计算模型的基本尺寸为10 m×10 m×10 m，井筒裸眼直径0.2 m，套管直径0.1 m，套管厚度0.008 m。假定套管与水泥环粘结完好。模型底面在z方向的位移为零，顶面受上覆岩体压力作用，四周表面水平位移为零，顶、底面为渗水边界，四周表面为不渗水边界，射孔深度分别取0.5 m、0.8 m和1.0 m，射孔直径分别取20 mm、25 mm和30 mm，定面射孔夹角分别取30°、45°和60°，井筒方位角分别为0°、45°、60°及90°，分析沿垂直面和水平面射孔两种情况。采用空间8节点结构化网格对几何模型进行剖分，为了提高计算精度，井筒直径2 m范围内网格细化，其他部分网格密度较低。

图1 地应力计算几何模型

考虑地层的改造过程，计算分为5步：①施加初始地应力场，模拟初始地层的赋存应力；②钻井过程：去除井筒位置处岩体，井筒的岩体壁面施加钻井液作用的液体压力及渗透压力；③下套管：在井筒内植入套管，套管壁面施加顶替液压力；④射孔：去除射孔孔眼处的岩体，在射孔孔眼壁面上施加液体压力和渗透压力；⑤压裂过程：在井筒及射孔孔眼表面上施加流体压力载荷，直至岩体发生破裂。

根据最大拉应力理论，当孔壁处最大拉应力大于岩石抗张强度时，裂缝起裂，则裂缝的起裂准则为：

1.3 实例验证

选取松辽盆地南部185区块某水平井进行模型验证，该井采用直径139.7 mm（5.5 in）套管，使用水泥固井完井，采用定面射孔+快钻桥塞多段（7段）多簇（17簇）压裂技术。对第1段进行模拟计算，其中油井垂直段深度1 477.4 m，水平井筒倾斜角为88.2°，水平段长度800 m，射孔井段深度2 370～2 374 m，采取6相位射孔，射孔密度12孔/m。该井储集层岩体的抗

拉强度为2.56 MPa，地层流体饱和度为100%，流体密度为1 000 kg/m3，初始孔隙压力为14.77 MPa，弹性模量22.6 GPa，泊松比0.22，最小主应力28 MPa，平均孔隙度17.6%，平均渗透率17.3×10-3μm2。

2013年10月25日对该井进行了压裂作业。图2为该井压裂施工曲线，可以看出：井口的破裂压力为30 MPa，延伸压力由30 MPa逐渐递减至25 MPa。由于该井垂直井深为1 477.4 m，考虑管柱阻力损失（每1 000 m约损失4 MPa），则裂缝起裂时作用在井下射孔孔眼位置处的液体压力约为35.67 MPa。

图2 第1井段压裂施工曲线

采用建立的定面射孔局部地应力计算模型，经反复试算，当施加在射孔孔眼壁面的液体压力为33.60 MPa时，射孔孔眼壁面的最大拉应力达到2.56 MPa，由（3）式可知，此时岩体发生拉伸破坏。因此，采用模型计算的起裂压力为33.60 MPa，与测试的起裂压力（35.67 MPa）相比，误差为5.8%，验证了模型的可靠性。

2 定面射孔水力裂缝起裂特征

为了分析定面射孔水力裂缝是否首先在射孔平面内起裂，设井筒方位角为0°，射孔沿z方向，定面射孔夹角30°，针对正断层型及逆断层型地应力场两种条件进行分析（正断层型地应力场：σz>σx>σy；逆断层型地应力场：σx>σy>σz）。对于正断层型地应力场，x、y、z方向初始地应力分别取35.6 MPa、29.9 MPa和46.5 MPa；对于逆断层型地应力场，x、y、z方向初始地应力分别取46.5 MPa、35.6 MPa和29.9 MPa。图3、图4分别为正断层型及逆断层型地应力场条件下射孔孔眼周围的最大主应力分布。

由图3a与图4a对比可知：采用定面射孔方式时，由于射孔孔眼间的相互影响，水力裂缝首先在射孔平面内相互贯通，形成扇形的破裂面，增加近井筒储集层的改造面积；正断层型地应力场条件下，最大主应力的等值线垂直于井筒分布，说明裂缝在与井筒垂直的平面内起裂的同时在井筒面内扩展，最终形成垂直于井筒的初始裂缝，而逆断层型地应力场条件下，最大主应力的等值线平行于井筒，说明裂缝在射孔面内先起裂，在垂直于井筒的平面内扩展，易形成转向裂缝。因此，逆断层型地应力场条件下水平井采用定面射孔方式时的起裂压力较为复杂。

由图3b与图4b对比可知，采用定面射孔方式时，正断层型地应力场条件下在射孔平面内形成了宽而短的扇形缝，而逆断层型地应力场条件下在射孔平面内形成了窄而长的扇形缝。因此，正断层型地应力场条件下且油气储集层较薄时，适合采用定面射孔方式。

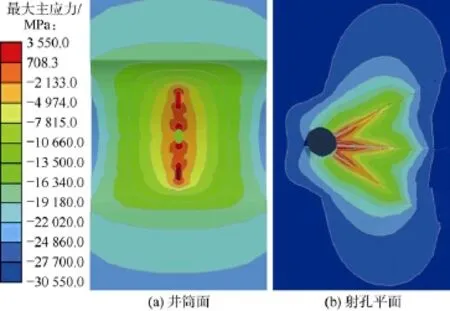
图3 正断层型地应力场条件下定面射孔最大主应力分布

图4 逆断层型地应力场条件下定面射孔最大主应力分布

3 定面射孔水力裂缝起裂压力影响因素

3.1 井筒方位角

井筒位置与储集层三向主应力的关系如图5所示，

定义井筒倾斜角γ为井筒轴线与垂直方向的夹角，定义井筒方位角θ为井筒轴线在水平面内的投影与水平最大主应力方向的夹角。计算时，假定井筒倾斜角为90°，井筒方位角分别为0°、30°、45°、60°、90°，射孔方式为螺旋射孔和定面射孔，分水平面内射孔和垂直面内射孔两种情况，计算模型共20个，计算结果见图6—图9。

图5 井筒位置与三向主应力关系

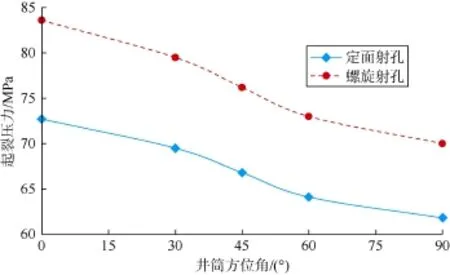
图6 正断层型地应力场水平射孔起裂压力与井筒方位角关系

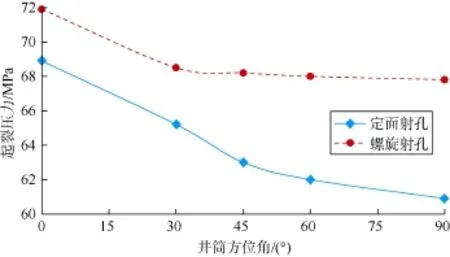
图7 正断层型地应力场垂直射孔起裂压力与井筒方位角关系

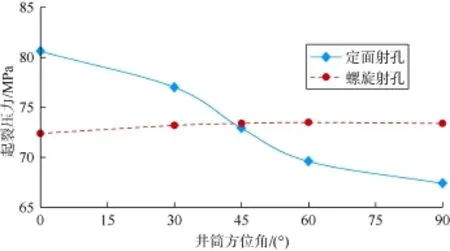
图8 逆断层型地应力场水平射孔起裂压力与井筒方位角关系

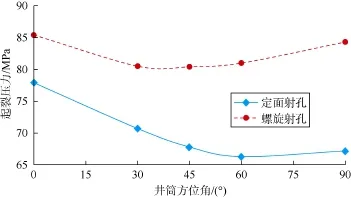
图9 逆断层型地应力场垂直射孔起裂压力与井筒方位角关系

由图6、图7可知，正断层型地应力场条件下，井筒倾斜角相同时：无论进行水平面内射孔还是垂直面内射孔，定面射孔的起裂压力均低于螺旋射孔的起裂压力；无论采用定面射孔还是螺旋射孔，垂直面内射孔的起裂压力均低于水平面内射孔的起裂压力。

由图8、图9可知，逆断层型地应力场条件下，井筒倾斜角相同时：采用水平面内射孔时，当井筒方位角大于45°时，定面射孔起裂压力小于螺旋射孔起裂压力，而在井筒方位角小于45°时，定面射孔起裂压力大于螺旋射孔起裂压力；采用垂直面内射孔时，不同井筒方位角下定面射孔起裂压力均低于螺旋射孔的起裂压力，井筒方位角越大，定面射孔的起裂压力越低。这是由于水平面内射孔时孔眼壁面上的最大主应力随着井筒方位角的增大分布得更加均匀（见图10），这样有助于孔眼间相互作用从而降低起裂压力，而垂直面内射孔时最大主应力受井筒方位角的影响较小。

3.2 井筒倾斜角

当井筒倾斜角为0时，井筒沿z方向，为垂直井；当井筒倾斜角为90°时，井筒沿x方向，为水平井。因此，计算时，假定井筒方位角为0，井筒倾斜角取50°、60°、70°、80°、90°，射孔方式为螺旋射孔和定面射孔，分水平面内射孔和垂直面内射孔两种情况，计算模型共20个，计算结果见图11—图14。

图10 孔眼最大主应力分布

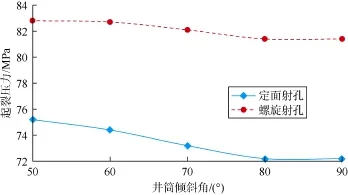
图11 正断层型地应力场水平射孔起裂压力与井筒倾斜角关系

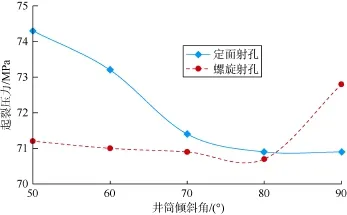
图12 正断层型地应力场垂直射孔起裂压力与井筒倾斜角关系

由图11和图12可知，正断层型地应力场条件下，井筒方位角相同时：在水平面内射孔时，不同井筒倾斜角下定面射孔起裂压力均低于螺旋射孔起裂压力，且倾斜角越大，井筒水平程度越好，定面射孔起裂压力越低；在垂直面内射孔时，当井筒倾斜角大于80°时定面射孔的起裂压力较低，当井筒倾斜角小于80°时定面射孔比螺旋射孔的起裂压力高。因此，正断层型地应力场条件下，在垂直面内定面射孔时，井筒倾斜角不宜小于80°。

由图13、图14可知，逆断层型地应力场条件下，井筒方位角相同时：在水平面内射孔时，井筒倾斜角大于60°时定面射孔起裂压力高于螺旋射孔起裂压力；在垂直面内射孔时，定面射孔起裂压力明显低于螺旋射孔起裂压力。

图13 逆断层型地应力场水平射孔起裂压力与井筒倾斜角关系

图14 逆断层型地应力场垂直射孔起裂压力与井筒倾斜角关系

3.3 射孔参数

3.3.1 射孔夹角

射孔夹角是定面射孔的重要参数，计算时选取射孔夹角为30°、40°、50°、60°，考虑正断层型及逆断层型地应力场两种情况，计算结果见图15。

图15 射孔夹角与起裂压力关系

由图15可知：随着射孔夹角的增大起裂压力逐渐增大，这是由于射孔夹角越大孔眼间相互影响越小，应力集中程度减弱，使得起裂压力增加。因此，在不考虑套管强度的条件下，孔眼分布得越密起裂压力越低；相同射孔夹角下，正断层型地应力场条件下起裂压力低于逆断层型地应力场起裂压力，这是由于逆断层型地应力场条件下孔眼间应力集中导致初始水力裂缝沿射孔平面起裂，而与最大主应力方向不一致。

3.3.2 射孔深度

计算时，假定射孔夹角为30°，射孔直径为25 mm，射孔深度为0.5 m、0.7 m、0.8 m、1.0 m，计算结果见图16。

图16 射孔深度与起裂压力关系

由图16可知：随着射孔深度的增加起裂压力减小。这是由于孔眼越深孔眼壁面的面积越大，相同水压下作用在孔眼壁面上的载荷越大，地层岩体越易起裂；相同射孔深度下，正断层型地应力场条件下起裂压力低于逆断层型地应力场起裂压力。

3.3.3 射孔直径

计算时，假定射孔夹角为30°，射孔深度为0.5 m，射孔直径分别为15 mm、20 mm、25 mm、30 mm，计算结果见图17。

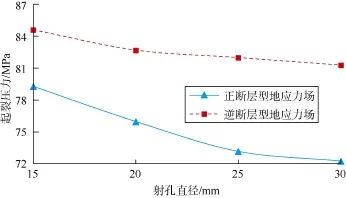
图17 射孔直径与起裂压力关系

由图17可知：随着射孔直径的增加起裂压力降低。这是由于射孔直径越大，平面内孔眼间距减小，孔眼的应力集中效应增大，同时孔眼壁面面积增大，水压作用效果增强，因此起裂压力降低；相同射孔直径下，正断层型地应力场条件下起裂压力低于逆断层型地应力场起裂压力。

4 结论

根据流固耦合理论，采用数值模拟技术，建立了水平井定面射孔局部地应力计算模型，确定了裂缝起裂准则。以吉林油田某定面射孔井为例对模型进行了验证，计算的起裂压力与测试结果相比误差为5.8%，证明了模型的可靠性。

采用建立的模型分析了定面射孔水力裂缝起裂特征，结果表明：对于正断层和逆断层这2种地应力场类型，采用定面射孔方式，均可实现裂缝首先在射孔平面上起裂，正断层型地应力场条件下可形成宽而短的垂直缝，逆断层型地应力场条件下易形成长而窄的转向缝。

采用建立的模型研究了井筒位置、射孔参数对定面射孔起裂压力的影响规律，结果表明：①井筒倾斜角一定时，随着井筒方位角的增加，定面射孔的起裂压力逐渐减小；对于正断层型地应力场，在水平面内射孔或垂直面内射孔时定面射孔起裂压力均低于螺旋射孔起裂压力；对于逆断层型地应力场，在水平面内射孔且井筒方位角大于45°时或在垂直面内射孔时，定面射孔起裂压力均低于螺旋射孔起裂压力。②定面射孔起裂压力对井筒倾斜角较为敏感：正断层型地应力场条件下，垂直射孔且井筒倾斜角大于80°或水平射孔时，定面射孔起裂压力低于螺旋射孔起裂压力；逆断层型地应力场条件下，水平射孔且井筒倾斜角小于60°或垂直射孔时，定面射孔起裂压力低于螺旋射孔起裂压力。③射孔夹角越小、射孔深度越大、射孔直径越大，定面射孔起裂压力越低。

符号注释：

f——介质体力矩阵，N/m3；I——单位矩阵；J——当前构型与参照构型的体积比；nw——孔隙比；p——流体孔隙压力，Pa；Smax——岩体壁面的最大主应力，计算中正为拉负为压，MPa；t——时间，s；t——表面力矩阵，N/m2；V——微元体体积，m3；vw——渗流速度向量，m/s；x，y，z——直角坐标系；x——空间向量，m；γ——井筒倾斜角，（°）；——虚应变矩阵，s-1；Dv——虚速度矩阵，m/s；θ——井筒方位角，（°）；ρw——液体密度，kg/m3；¢——有效应力

矩阵，Pa；σt——岩体的抗拉强度，由实验测定，MPa；σx，σy，σz——x，y，z轴方向的初始地应力，MPa；Ω——微元体表面积，m2。

[1] 马旭,郝瑞芬,来轩昂,等.苏里格气田致密砂岩气藏水平井体积压裂矿场试验[J].石油勘探与开发,2014,41(6): 742-747.Ma Xu,Hao Ruifen,Lai Xuan’ang,et al.Field test of volume fracturing for horizontal wells in Sulige tight sandstone gas reservoirs[J].Petroleum Exploration and Development,2014,41(6): 742-747.

[2] Meyer B R,Bazan L W,Jacot R H,et al.Optimization of multiple transverse hydraulic fracture in horizontal wellbore[R].SPE 131732,2010.

[3] 张矿生,王文雄,徐晨,等.体积压裂水平井增产潜力及产能影响因素分析[J].科学技术与工程,2013,13(35): 10475-10480.Zhang Kuangsheng,Wang Wenxiong,Xu Chen,et al.Analysis on stimulation potential and productivity influencing factors of network fractured horizontal well[J].Science Technology and Engineering,2013,13(35): 10475-10480.

[4] Mayerhofer M J,Lolon E P,Warpinski N R,et al.What is simulation reservoir volume?[J].SPE Production &Operations,2010,25(1): 89-98.

[5] 胡广军,彭原平,周绪国.垂直井定向射孔技术[J].新疆石油科技,2007,17(4): 10-16.Hu Guangjun,Peng Yuanping,Zhou Xuguo.Vertical well oriented perforating technology[J].Xinjiang Petroleum Science &Technology,2007,17(4): 10-16.

[6] 袁彬,苏玉亮,丰子泰,等.体积压裂水平井缝网渗流特征与产能分布研究[J].深圳大学学报: 理工版,2013,30(5): 545-550.Yuan Bin,Su Yuliang,Feng Zitai,et al.Productivity distribution and flow characteristics of volume-fractured horizontal wells[J].Journal of Shenzhen University: Science and Engineering,2013,30(5): 545-550.

[7] 刘合,王峰,王毓才,等.现代油气井射孔技术发展现状与展望[J].石油勘探与开发,2014,41(6): 731-737.Liu He,Wang Feng,Wang Yucai,et al.Oil well perforation technology: Status and prospects[J].Petroleum Exploration and Development,2014,41(6): 731-737.

[8] 陈峥嵘,邓金根,朱海燕,等.定向射孔压裂起裂与射孔优化设计方法研究[J].岩土力学,2013,34(8): 2309-2316.Chen Zhengrong,Deng Jin’gen,Zhu Haiyan,et al.Research on initiation of oriented perforation fracturing and perforation optimization design method[J].Rock and Soil Mechanics,2013,34(8): 2309-2316.

[9] 王磊,张乐宇,李菁菁,等.水平射孔井射孔参数及起裂压力研究[J].重庆科技学院学报: 自然科学版,2013,15(5): 2309-2316.Wang Lei,Zhang Leyu,Li Jingjing,et al.Research of perforation parameters and initiation pressure for horizontal perforated wells[J].Journal of Chongqing University of Science and Technology: Natural Sciences Edition,2013,15(5): 2309-2316.

[10] Hossain M M,Rahman M K,Rahman S S.A comprehensive monograph for hydraulic fracture initiation from deviated wellbores under arbitrary regimes[R].SPE 54360,1999.

[11] 彪仿俊,刘合,张劲,等.螺旋射孔条件下地层破裂压力的数值模拟研究[J].中国科学技术大学学报,2011,41(3): 219-226.Biao Fangjun,Liu He,Zhang Jin,et al.A numerical study of fracture initiation pressure under helical perforation conditions[J].Journal of University of Science and Technology of China,2011,41(3): 219-226.

[12] 王素玲,董康兴,董海洋,等.低渗透储层射孔参数对起裂压力的影响[J].石油钻采工艺,2009,31(3): 85-89.Wang Suling,Dong Kangxing,Dong Haiyang,et al.Effect analysis of perforating parameters upon initiation pressure in low permeability reservoir[J].Oil Drilling &Production Technology,2009,31(3): 85-89.

[13] 金衍,张旭东,陈勉,等.天然裂缝地层中垂直井水力裂缝起裂压力模型研究[J].石油学报,2005,26(6): 113-118.Jin Yan,Zhang Xudong,Chen Mian,et al.Initiation pressure models for hydraulic fracturing of vertical wells in naturally fractured formation[J].Acta Petrolei Sinica,2005,26(6): 113-118.

[14] 张广明,刘合,张劲,等.水平井水力压裂的三维有限元数值模拟研究[J].工程力学,2011,28(2): 101-106.Zhang Guangming,Liu He,Zhang Jin,et al.Three-dimensional finite element numerical simulation of horizontal well hydraulic fracturing[J].Engineering Mechanics,2011,28(2): 101-106.

[15] 杨野,彪仿俊,王瀚,等.螺旋射孔对水平缝水力压裂过程影响的数值模拟[J].石油学报,2012,33(6): 1076-1079.Yang Ye,Biao Fangjun,Wang Han,et al.A numerical study on effects of helical perforation on hydraulic fracturing of horizontal fractures[J].Acta Petrolei Sinica,2012,33(6): 1076-1079.

（编辑 胡苇玮）

Hydraulic fracture initiation mechanism in the definite plane perforating technology of horizontal well

Liu He1,Lan Zhongxiao2,Wang Suling3,Xu Jianguo4,Zhao Chenxu4
(1.PetroChina Research Institute of Petroleum Exploration &Development,Beijing 100083,China;2.PetroChina Daqing Oilfield Company limited,Daqing 163000,China;3.College of Mechanical Science and Engineering,Northeast Petroleum University,Daqing 163318,China;4.Jilin Oilfield Production Engineering Research Institute,Songyuan 138000,China)

The local stress calculation model of the definite plane perforation for the horizontal wells was built,and the mechanism of fracture initiation and the influence rules of the wellbore location and perforating parameters on the fracture initiation pressure were analyzed.The in-situ stress model of three-dimensional fluid-solid coupling was established according to the theory of percolation mechanics,and the method for determining the initiation pressure of the definite plane perforation was presented according to the maximum tensile stress theory and was verified by application example.The calculation and analysis reveal: for the in-situ stress fields of normal faults and reverse faults,the initiation of hydraulic fractures happens on the perforated plane during the definite plane perforation,a wide,short,vertical fracture forms in the in-situ stress field of a normal fault,and a narrow,long,diverted fracture forms in the in-situ stress field of a reverse fault;for the in-situ stress field of a normal fault,the greater the wellbore azimuth and inclination angle are,the lower the initiation pressure is;for the in-situ stress field of a reverse fault,the larger the wellbore azimuth angle or the smaller the wellbore inclination angle is,the lower the initiation pressure is;the smaller the perforation angle,the greater the perforating depth,or the larger the perforation diameter is,the lower the initiation pressure of definite plane perforation is.

definite plane perforation;hydraulic fracturing;volume fracturing;fracture initiation mechanism;fracture initiation pressure

国家重点基础研究发展计划（973）项目（2015CB250900）；国家自然科学基金（51374074）

TE257.1

A

1000-0747(2015)06-0794-07

10.11698/PED.2015.06.13

刘合（1961-），男，黑龙江哈尔滨人，博士，中国石油勘探开发研究院教授级高级工程师，主要从事低渗透油气藏增产改造、机采系统提高系统效率、分层注水和井筒工程控制技术等方面的研究工作。地址：北京市海淀区学院路20号，中国石油勘探开发研究院院办，邮政编码：100083。E-mail: liuhe@petrochina.com.cn

联系作者：王素玲（1975-），女，博士，东北石油大学机械科学与工程学院教授，主要从事油气田地面工程方面的教学和研究工作。地址：黑龙江省大庆市高新技术开发区发展路199号，东北石油大学机械科学与工程学院，邮政编码：163318。E-mail: wsl1028@163.com

2014-12-29

2015-05-19