变分不等式的近似解与向量优化问题的拟近似解的关系

岳瑞雪，李小燕，高 英

(重庆师范大学数学学院，重庆 401331)

在最优化理论中，凸性假设被广泛应用。为了更好地解决现实问题，一些学者对凸函数做了一系列推广。Mangasarian［1］给出了伪凸函数的概念。Ngai等［2］给出了近似凸函数的概念。Bhatia等［3］和Gupta 等［4］利用 Clarke 次微分对近似凸函数进行了推广。

Giannessi［5］给出了欧几里得空间中的向量值变分不等式问题。由于向量值变分不等式问题在许多领域都有重要的应用价值和理论价值，因此，一些学者对向量变分不等式问题作了很多推广，见文献［6－9］。变分不等式问题是解决向量优化问题的一个有效工具。近年来，一些学者在研究向量优化问题时发现多目标优化问题的最优性条件可以通过变分不等式进行刻画，见文献［5，10－14］。Yang和Zheng［15］研究了一个点是向量变分不等式问题近似解的充分和必要条件。Lee和Lee［16］研究了几种向量变分不等式问题和非光滑向最优问题之间的联系。在向量优化问题中，在非紧的情况下，有效解(弱有效解)往往不一定存在，近似解在很弱的情况下都可能存在 (Ekelend变分原理)。Loridan［17］介绍了一般多目标优化问题的ε－有效解的概念，并研究了ε－有效解的一些性质。Beldiman［18］等给出了多目标优化问题(on，¯ε)－拟近似 (弱，真) 有效解的概念。Mishra等［19］研究了向量变分不等式的解和向量优化问题局部拟有效解之间的关系。

本文在文献［19］的基础上研究了变分不等式问题的近似解与非光滑向量优化问题拟近似有效解之间的联系。

1 预备知识

设Rn是 n维欧几里得空间是 Rn的非负象限;〈·，·〉表示欧几里得内积，‖·‖ 表示欧几里得范数;X⊆Rn是非空闭凸集合。

本文给出以下符号:对任意的 x，y∈Rn，有

x=y ⇔ xi=yi，∀i=1，…，n

x ＞ y⇔ xi＞ yi，∀i=1，…，n

x≧ y ⇔ xi≧ yi，∀i=1，…，n

x≥ y ⇔ xiyi，∀i=1，…，n，且 x≠ y

定义1［20］函数 f:X→R被称为在 x∈X附近的Lipschitz函数。如果存在一个正常数K和一个 x的邻域 N，使得对于任意的 y，z∈N，有|f(y)－f(z)|≤K‖y－z‖。如果对于任意的 x∈X，f:X→R是在 x附近的 Lipschitz函数，则称函数f是在X上的局部Lipschitz函数。

定义2［20］设f:X→R是在 X上的局部Lipschitz函数。f在 x∈X处沿方向 v∈Rn的 Clarke广义方向导数记为 fo(x;v)，定义为 fo(x;v)=

定义3［20］设f:X→R是在X上的局部Lipschitz函数。f在 x∈X处的 Clarke广义次微分记为 ∂cf(x)，定义为∂cf(x)={ξ∈Rn:fo(x;v)≥〈ξ，v〉，∀v∈Rn}。

这些定义和性质可以推广到局部Lipschitz的向量值函数 f:X→Rp，fi(i=1，…，p)为 f的分量。f在 x∈X处的 Clarke广义次微分为 ∂cf(x)=∂cf1(x)×∂cf2(x)×… ×∂cfp(x)。

定义4［1］集合∅≠X⊆Rn为凸集，如果x+λ(y－x)∈X，x，y∈X，λ∈［0，1］。

定义5［19］设f:X→Rp是在X上的局部Lipschitz函数。f为在y∈X处的拟近似凸函数，若对于任意的 α∈int(Rp+)，存在 δ＞0，使得

称f为 X上的近似凸函数，若对于任意的 y∈X，f在y∈X处是近似凸函数。

定义6［19］设f:X→Rp是在X上的局部Lipschitz函数。f为在y∈X处的严格拟近似凸函数，若对于任意的 α∈int(Rp+)，存在 δ＞0，使得

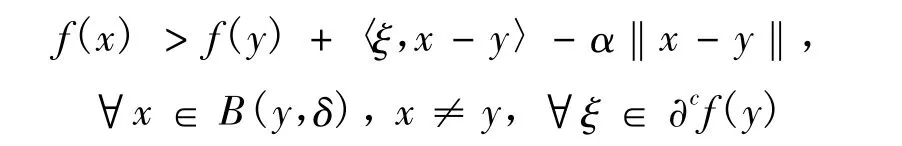
称f为X上的严格近似凸函数，若对于任意的y∈X，f在 y∈X处是严格近似凸函数。

定义7［19］设 f:X→Rp是在 X上的局部Lipschitz函数。f为在 y∈X处的拟近似伪凸函数，如果对于任意的 α∈int(Rp+)，存在 δ＞0，使得∀x∈B(y，δ)，

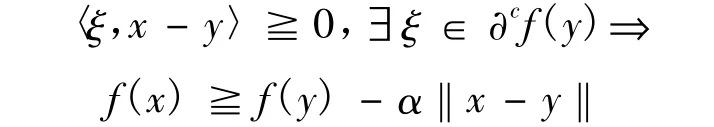
或者

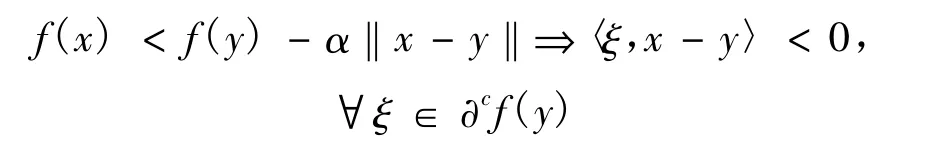
则称f为X上的拟近似伪凸函数，对于任意的y∈X，f在 y∈X处是拟近似伪凸函数。

为了研究向量优化问题的拟近似弱有效解与临界点之间的关系，给出了拟近似伪凸的定义。

定义8设f:X→Rp是在X上的局部Lipschitz函数。f称为在y∈X处的拟近似伪凸函数，若对于任意的 α，∈int(Rp+)，存在 δ＞0，使得∀x∈B(y，δ)

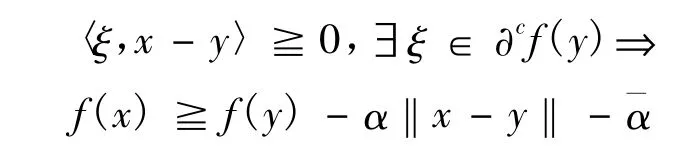
或者

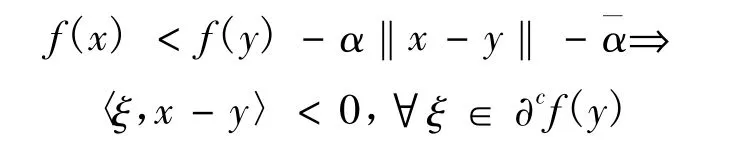
则称f为X上的拟近似伪凸函数，对于任意的y∈X，f在 y∈X处是拟近似伪凸函数。

考虑如下的非光滑向量优化问题:

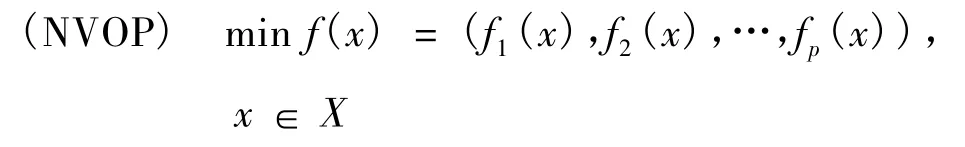
其中fi:X→R，i=1，2，…，p是 X 上的局部 Lipschitz函数。

定义 9［18］

1)称y∈X是(NVOP)的拟近似有效解，如果存在 α∈int(Rp+)∈int()，对于任意的 x∈X，下面不等式不成立:f(x)≤f(y)－α‖x－y‖－。

2)称y∈X是(NVOP)的拟近似弱有效解，如果存在 α∈int()¯∈int()，对于任意的 x∈X，下面不等式不成立:f(x) ＜f(y)－α‖x－y‖ －。

考虑如下的变分不等式问题［19］:

(VVIP)寻找 y∈X，使得对于任意的 x∈X有〈ξ，x－y〉≤0，∀ξ∈∂cf(y)。

(WVVIP)寻找y∈X，使得对于任意的 x∈X有〈ξ，x－y〉＜0，∀ξ∈∂cf(y)。

定义10

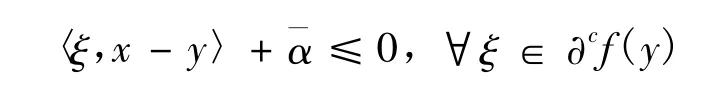
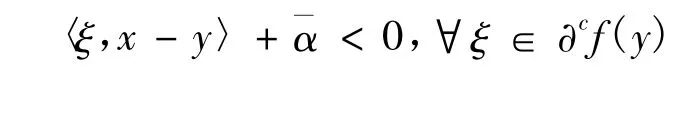
2 近似向量变分不等式问题与非光滑向量优化问题之间的联系

文献［19］研究了变分不等式问题的解与非光滑向量优化问题的局部拟 (弱)有效的关系。本节研究了向量变分不等式问题的近似解与非光滑向量优化问题的拟近似解的关系和向量优化问题的临界点与拟近似弱有效解的关系。

定理1设f:X→Rn在y∈X处是近似凸的。若y是(VVIP)的近似解，则y是 (NVOP)的拟近似有效解。

证明若y不是(NVOP)的拟近似有效解，则对于任意的 α，∈int(Rp+)，存在 x∈X，使得 f(x)≤f(y)－α‖x－y‖－。因为 f在 y∈X 处是近似凸的，即对于任意的 α∈int(Rn+)，存在 δ＞0，使得对于任意的 x∈B(y，δ)∩X 有

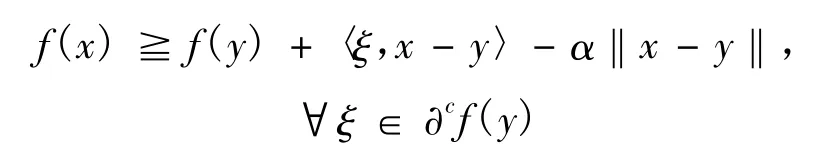
定理2

1)设y∈X是(NVOP)的拟近似弱有效解，则y是(WVVIP)的近似解。

2)设f:X→Rn在y∈X处是近似凸的。若 y是(WVVIP)的近似解，则y是 (NVOP)的拟近似弱有效解。

证明

1)因为y是(NVOP)的拟近似弱有效解，X是凸集，所以存在 α，∈int(Rp+)，使得对于任意的x∈X，下面不等式不成立:

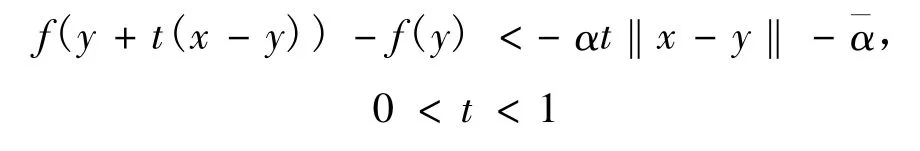
上式两边同时除以 t，然后让 t↓0取极限，得fo(y，x－y) ＜－，从而有

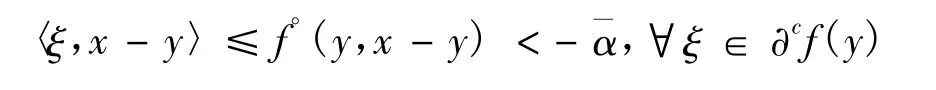
故y是(AWVVIP)的解。

2)与定理1的证明类似。

定理3设f:X→Rn在y∈X处是严格近似凸的。若y是(NVOP)的拟近似弱有效解，则y是(NVOP)的拟近似有效解。

证明:若y不是(NVOP)的拟近似有效解，则对于任意的 α，∈int()，存在 x∈X，使得f(x)≤f(y)－α‖x－y‖－。因为f在y∈X处是严格近似凸的，即对于任意的 α∈int()，存在 δ＞0，使得对于任意的 x∈B(y，δ)∩X有

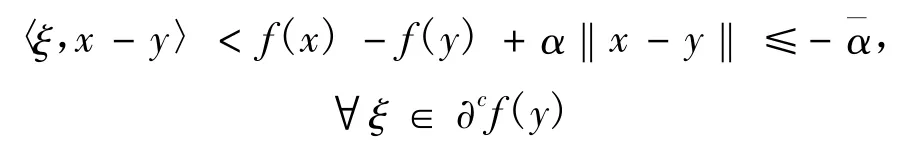
从而y不是(WVVIP)的近似解。又由定理2的1)可知，y∈X不是(NVOP)的拟近似弱有效解，这与条件矛盾，故y是(NVOP)的拟近似有效解。

定义11 称可行点y∈X是(NVOP)的临界点，如果存在 λ∈ Rp，λ≥0，使得 λTξ=0，∀ξ∈∂cf(y)。

定理4设 f:X→Rn在 y∈X处是近似伪凸的，若 y∈X是 (NVOP)的临界点，则y是(NVOP)的拟近似弱有效解。

证明 若y∈X是 (NVOP)的临界点，则存在 λ∈Rp，λ≥0，使得 λTξ=0，∀ξ∈∂cf(y)，从而对于任意的 x∈X，有〈λTξ，x－ y〉=0，∀ξ∈∂cf(y)，所以，对于任意的 x∈X，有〈ξ，x－ y〉≧0，∀ξ∈∂cf(y)。又因为f在y∈X处是近似伪凸的，所以对于任意的 α∈int(Rp+)，存在

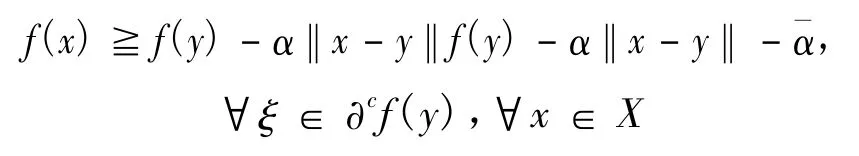
故y是(NVOP)的拟近似弱有效解。

定理5 若(NVOP)的临界点是(NVOP)的拟近似弱有效解，则f:X→Rn在 y∈X处是拟近似伪凸的。

证明设(NVOP)的临界点y是(NVOP)的拟近似弱有效解。若y∈X是(NVOP)的临界点，则存在 λ∈Rp，λ≥0，使得 λTξ=0，∀ξ∈∂cf(y)，

从而对于任意的 x∈X，有〈λTξ，x－y〉=0，∀ξ∈∂cf(y)，即对于任意的 x∈X，有〈ξ，x－y〉≧0，∀ξ∈∂cf(y)。又因为 y∈X是 (NVOP)的拟近似弱有效解，则存在 α∈int()∈int()，对于任意的x∈X，有f(x)≧f(y)－α‖x－y‖ －α¯，所以f在临界点y∈X处是拟近似伪凸的。

［1］Mangasarian O L.Nonlinear Programming［M］.New York:McGraw-Hill，1969.

［2］Ngai H V，Luc D T，Thera M.Approximate convex functions［J］.J.Nonlinear Convex Anal，2000，1:155-176.

［3］Bhatia D，Gupta A，Arora P.Optimality via generalized approximate convexity and quasiefficiency［J］.Optimization Letters，2013，7(1):127-135.

［4］Gupta A，Mehra A，Bhatia D.Approximate convexity in vector optimization［J］.Bull.Aust.Math.Soc，2006，74:207-218.

［5］Giannessi F.Theorems of alternative，quadratic programs and complementarity problems［J］.Variational inequalities and complementarity problems，1980，1:151-186.

［6］Dafermos S.Exchange price equilibrium and variational inequalities［J］.Math.Program，1990，46:391-402.

［7］Giannessi F.On Minty variational principle［M］//New Trends in Mathematical Programming.Dordrecht:Kluwer Academic Publishers，1997.

［8］Kinderlehrer D，Stampacchiya G.An Introduction to Variational Inequality and their Applications［M］.London:Academic Press，1980.

［9］Yang X Q，Goh C J.On vector variational inequalities:application to vector equilibria［J］.Journal of Optimization Theory and Applications.1997，95(2):431-443.

［10］Chen G Y，Craven B D.A vector variational inequality and optimization over an efficient set［J］.Z.Oper.Res，1990，34:1-12.

［11］Kinderlehrer D，Stampacchiya G.An Introduction to Variational Inequality and their Applications［M］.London:Academic Press，1980.

［12］Lee G M，Kim D S，Lee B S，et al.Vector variational inequality as a tool for studying vector optimization problems［J］.Nonlinear Anal，1998，34:745-765.

［13］Mishra S K，Wang S Y.Vector variational like inequalities and nonsmooth vector optimization problems［J］.Nonlinear Anal，2006，64:1939-1945.

［14］Yang X Q.Vector variational inequality and vector pseudolinear optimization［J］.J.Optim.TheoryAppl，1997，95:729-734.

［15］Yang X Q，Zheng X Y.Approximate solutions and optimality conditions of vector variational inequalities in Banach spaces［J］.J.Glob.Optim，2008，40:455-462.

［16］Lee G M，Lee K B.Vector variational inequalities for nondifferentiable convex vector optimization problems［J］.Journal of Global Optimization，2005，32(4):597-612.

［17］Sawaragi and Yoshikazu，Date.Theory of multiobjective optimzation［M］.Japan:Department of Applied Matheatics Konan Uinversity，1985.

［18］Beldiman M，Panaitescu E，Dogaru L.Approximate quasi efficient solutions in multiobjective opti-mization［J］.Bull.Math.Soc.Math.Roumanie Tome，2008，51(99):109-121.

［19］Mishra S K，Upadhyay B B.Some relations between vector variational inequality problems and nonsmooth vector optimization problems using quasi efficiency［J］.Positivity.2013，17:1071-1083.

［20］Clarke F H.Optimization and Nonsmooth Analysis［M］.New York:Wiley-Interscience，1983.