重力势能对注汽井热力计算的影响

舒华文，孙宪航

(1.中国石油大学(华东)储运与建筑工程学院，山东青岛 266580;2.中国石化胜利油田分公司滨南采油厂，山东滨州 256606)

注蒸汽开采是稠油开采的主要技术措施，在国内外稠油油田开发中得到了广泛应用。井底蒸汽干度是影响注汽采油效果的主要因素。而由于高温、高压、井深等条件限制，不可能每次注汽都完成井底蒸汽干度测试，因此，应用计算模型预测就成了一种可行的技术。利用能量守恒和动量守恒原理，结合流体力学和传热学理论，建立蒸汽压力、温度和干度沿程变化的模型，编制相应的计算程序计算蒸汽的某些参数，通过有限的现场测量数据修正某些系数，达到正确的预测目的［1］。目前，文献中的能量方程认为热焓远大于重力做功，忽略重力做功的影响，本文认为注蒸汽井热力计算过程中与重力做功相比较的不是蒸汽的比焓，而是平摊到单位质量蒸汽的热损失。这样，在一些情况下，不计重力做功会导致较大的误差。本文首先利用国内某油田五口注汽井4参数测试结果验证了程序模型，在此基础上，分析了不同级别的隔热油管忽略重力做功所导致的误差，从而验证了计入重力做功的必要性。

1 计算模型

1.1 能量方程

注汽井管柱传热包括隔热油管、套管、水泥环底层构成的内边界对流换热、外边界无限大的复合传热系统，其结构如图1所示。为了简化计算，假设从油管到水泥环外侧的传热为稳态径向传热，从水泥环外侧到地层无穷远处为非稳态径向导热，忽略沿深度方向的传热，蒸汽流动为稳定流，其参数在计算时刻仅随深度而变化。

分析图1所示微元体，坐标沿流动方向，根据能量守恒得［2］:

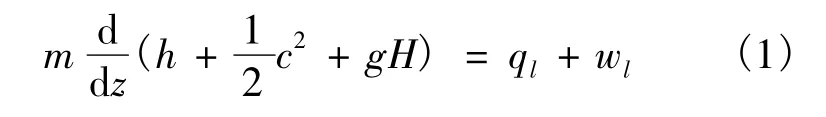
其中:m为蒸汽的流量(kg·s－1);h为蒸汽的比焓(J·kg－1);ql为单位长度的吸热速度(W·m－1);wl为单位长度上蒸汽对外做功(W·m－1);H为标高(m);注汽过程中蒸汽不对外做功，故wl=0，但会散热，故ql≠0。

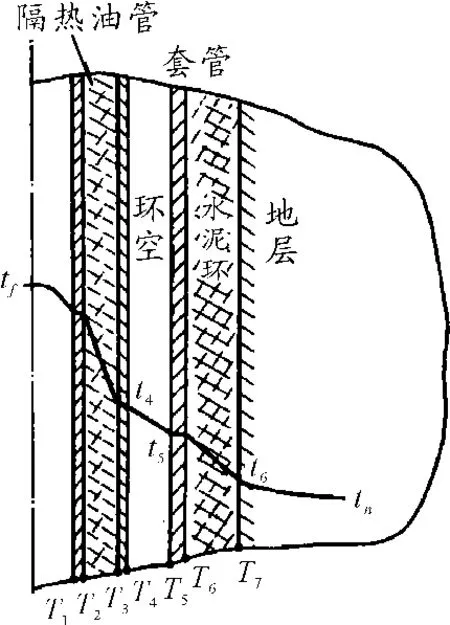
图1 注汽井结构示意图

现有文献中根据等号左边括号中3项数量级的大小进行简化，例如对蒸汽其比焓h≈2.0×106J·kg－1，动能 c2/2≈1/2 × 100=50 J·kg－1的量级，地面系统流体流动起点、终点标高不过几十米，故势能为100～1000 J·kg－1的量级，与比焓相比，似乎可以忽略。虽然文献中经常这样处理，但有一个原则错误，式(1)等号左边表达的是变量随坐标的变化率而不是变量本身，即

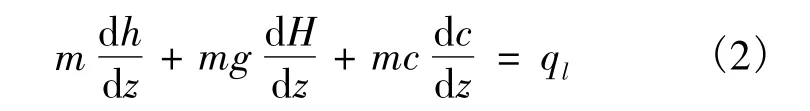
由此可见，没有理由能说明式(2)中等号左边哪项主要、哪项次要。对于动能项，因为流速变化很小，即dc/dz=0，故可忽略;对于重力势能项，dH/dz=－1，故重力势能变化率为－mg，其数值未必不与mdh/dz在同一量级上。

1.2 动量方程

蒸汽在井筒内流动属于管内气液两相流，其描述压力变化的方程［3］为:

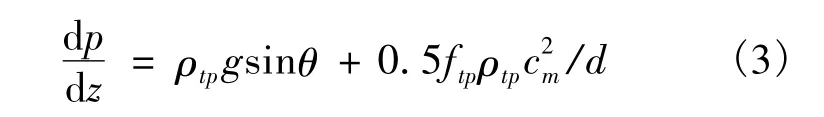
其中:ρtp为两相流当地密度(kg·m－3);ftp为两相流摩阻系数;cm为蒸汽平均流速(m·s－1);d为油管内径(m)。

两相流与单相流不同，当地密度和两相摩阻系数与流型有关。本文采用Hassan-Kabir给出的模型计算，详见文献［4］。

1.3 传热计算

式(2)中的单位长度的散热量 ql计算如下［5］:

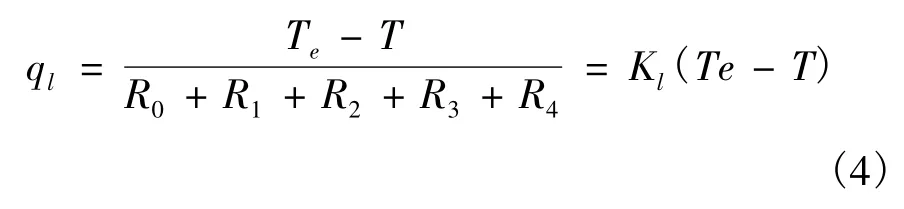
其中:R0，R1，R2，R3，R4分别为管内蒸汽对流换热热阻、隔热油管导热热阻、环空当量导热热阻、水泥环导热热阻和地层导热热阻(℃·m·W－1);Te为地层无穷远处的温度(℃);T为蒸汽温度(℃)。

其中:d4为套管外径;d5为水泥环外径;d1为隔热油管内径;d2为其外径;d3为套管内径;f(td)为地

需要说明的是:环空当量导热热阻包括环空内流体自然对流、导热和热辐射3种机制，其计算见参考文献［6］。因此，能量方程(1)可改写为

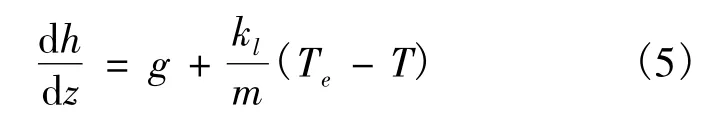
式(5)表明:传热系数kl小或注汽流量m大时，重力势能对蒸汽焓变的影响趋于增加。注汽井热力计算的定解条件为

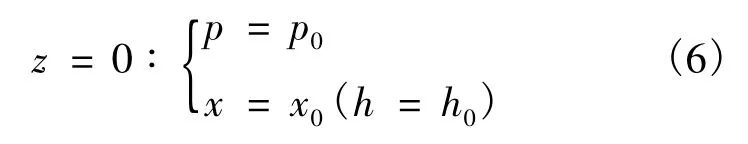
式(6)中x0为井口蒸汽干度。将式(3)～(5)和(6)结合，原则上可得蒸汽参数沿程分布。

1.4 干度和温度计算

求解式(3)和式(5)给出沿程比焓和压力分布，但式(5)中还出现蒸汽温度T，而T不是求解变量，故需要利用热力学关系获得T和干度x。这个问题相当于已知p，h求T和x。热力学原理表明:蒸汽状态参数只有2个自由度，即已知热力学参数中的2个，就可计算其他参数。根据定义h=xh″+(1－ x)h'h″=h″(p)，h'=h'(p)为饱和汽和饱和水的比焓，均为压力的函数。蒸汽温度等于其饱和温度，T=Ts(p)。h″(p)、h'(p)和Ts(p)已有精度很高的经验公式可用［7］。

1.5 计算方法

已知井口蒸汽干度、压力，求蒸汽参数沿程分布，就是求解关于h和P一个非线性的常微分方程组，采用数值计算求解。首先，将井筒从井口到井底分为N个节点。节间距为Δz，利用龙格－库塔法［8］逐点计算 pi，hi，再由 pi，hi得到 Ti，xi，最终得到 P，h，x，T 沿程分布。

2 计算示例

2.1 模型验证

某油田56－15－X井，该井热敏封隔器位于井深1120 m处，隔热油管视导热系数 λins=0.056 W·m－1·k－1;隔热油管内径为 62.5 mm，外径为114.3 mm，套管内径为161 mm，外径为177.8 mm，水泥环直径为245 mm，油管外表面和套管内表面黑度为0.85，地表年平均温度为17℃，地温梯度为0.035℃·m－1，地层导热系数为1.745 W·m－1·℃，地层导温系数 a=1.027 ×10－6m2·s－1，水泥环导热系数 λcem=1.0 W·m－1·℃，注汽流量m=7.8 t/h，井口蒸汽干度x0=0.64，压力p0=5.66 MPa。

图2给出了蒸汽压力分布曲线，可以看出趋势吻合得非常好。

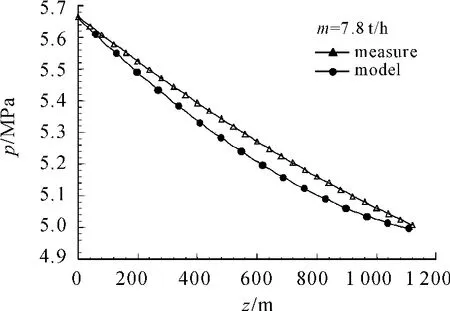
图2 模型计算压力与测试压力对比

在深度602 m处的压力误差最大，模型计算压力为 5.207 MPa，测量结果为 5.27 MPa，二者相差0.063 MPa，相对误差为1.195%，吻合得很好。

图3给出了蒸汽温度分布曲线，可以看出趋势吻合得非常好。

蒸汽的干度大于零，压力与温度一一对应，误差也是在600 m深处附近最大，测量值与计算值相差不到1℃，其相对误差更小。

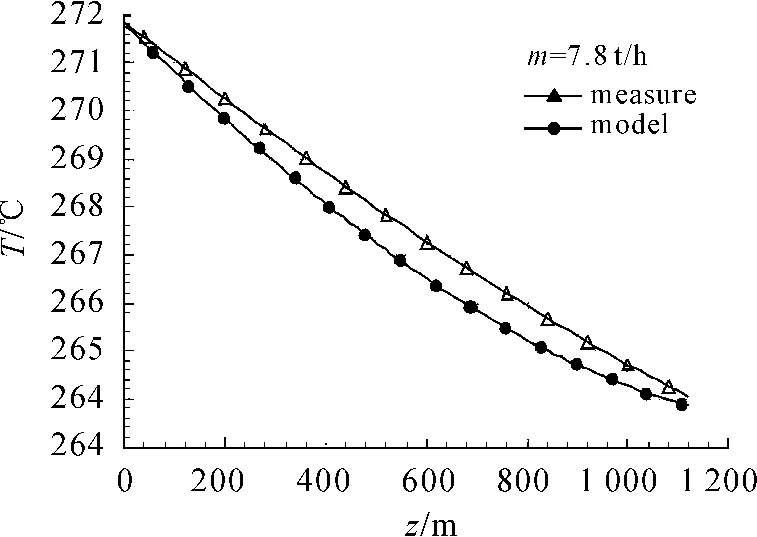
图3 温度分布模型结果与测量结果对比

图4给出了蒸汽干度分布曲线，可以看出趋势吻合得较好。

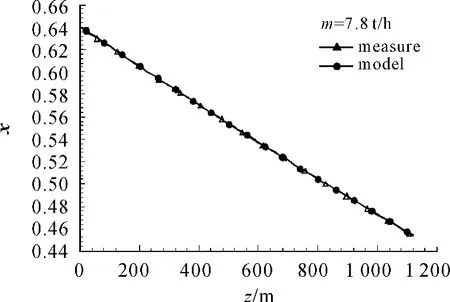
图4 蒸汽干度模型结果与测量结果对比

图4表明蒸汽干度与测量数值吻合较好。原因是隔热油管的导热系数是通过测量压力、温度和干度反推所得。实际注汽井不可能提供详细的隔热油管导热系数资料，该井测试数据为20 m一个测点，提供压力、温度和干度数值。因此，可获得蒸汽的比焓分布。由蒸汽的比焓分布可以得到井筒的总传热系数，再根据各环节的热阻计算方法获得平均的隔热油管视导热系数［9］。

2.2 重力做功的影响

为了分析能量守恒方程中忽略重力势能造成的影响，分析计算得注汽流量为23 t/h，假设该井分别用E级隔热油管和实际测试获得导热系数的隔热油管注汽，计算分析了蒸汽压力分布和干度分布的差别。图5给出了蒸汽压力分布的变化，可以看出:能量方程中是否考虑重力势能对计算的压力分布的影响不大。

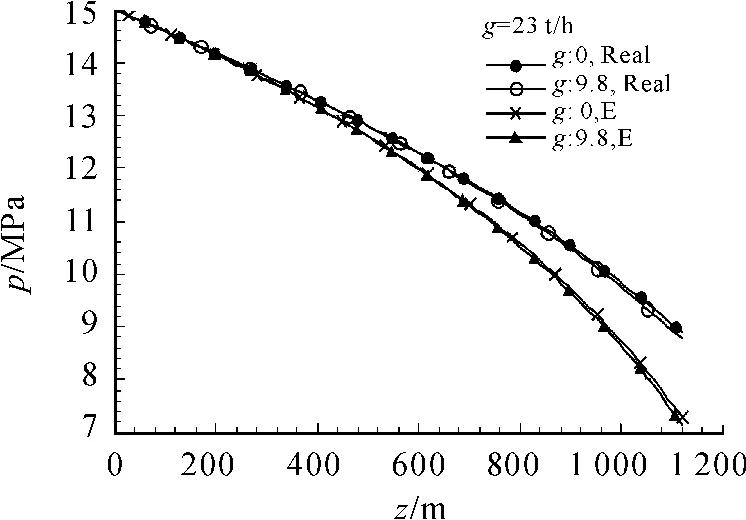
图5 重力势能对蒸汽压力分布的影响

需要说明的是:这里的重力势能是指能量方程中的项而不是压力控制方程中的重力势能项，因此在压力计算中必须考虑重力势能的影响［10］。图标中的E表示采用E级隔热油管注汽;g:0表示不考虑重力势能;g:9.8表示考虑重力势能的影响;Real表示采用根据4参数测试结果获得导热系数的隔热油管注汽。图6给出了E级隔热油管［11］注汽蒸汽干度分布的情况。

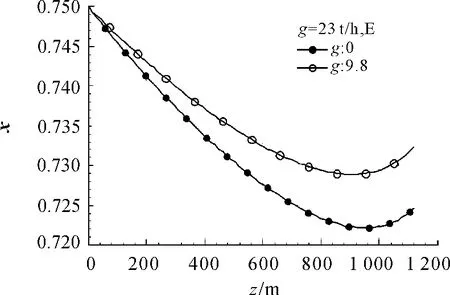
图6 采用E级隔热油管注汽蒸汽干度分布对比

图6表明:在能量方程中考虑与不考虑重力势能，E级隔热油管注汽后到达井底的蒸汽干度相差近1%，一个注汽周期后，进入到油层的热量会有较大的差别。

图7给出了隔热油管导热系数为0.056 W·m－1· K－1时的情况，相当于 B 级隔热油管［12］。

图7表明:采用B级隔热油管注汽，井底蒸汽干度相差较小，接近于0.8%的级别。能量方程表明:隔热油管导热系数越小，注汽流量越大，能量方程中考虑重力势能的影响越有必要，其他情况不再罗列。

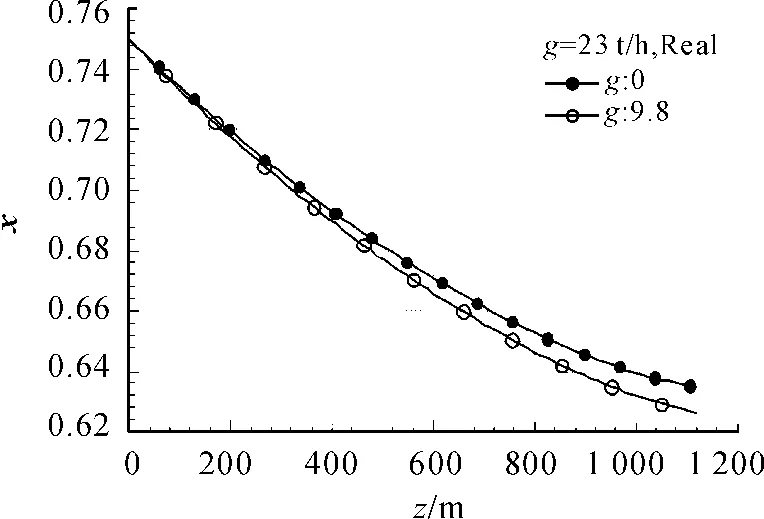
图7 采用B级隔热油管注汽蒸汽干度分布对比

3 结束语

注汽井井筒热力参数预测对于注汽分析是注汽效果分析主要的基础参数之一，在注汽计算模型的能量方程中考虑重力势能项是必要的，在高级别隔热油管注汽或者高注汽流量的情况下尤其必要。在注汽流量为23 t/h、井深为1120 m的情况下，无论是E级隔热油管还是B级隔热油管注汽，计与不计重力势能的影响，计算井底蒸汽干度相差1%左右。

［1］万仁溥，罗英俊.采油技术手册，第八分册，稠油热采工程技术［M］.北京:石油工业出版社，1996.

［2］王弥康.注汽井井筒热传递的定量计算［J］.石油大学学报，1994，18(4):77－82.

［3］Dukler A E，Wickes M III，Cleveland R G.Frictional Pressure Drop in Two-Phase Flow:B.An Approach Through Similarity Analysis［J］.AIChE J，1964，10(1):44.

［4］Hasan A R，Kabir C S，Sayarpour M.A basic approach to wellbore two-phase flow modeling［C］//SPE Annual Technical Conference and Exhibition.USA: ［s.n.］，2007.

［5］杨世铭，陶文铨.传热学［M］.3版.北京:高等教育出版社，1998.

［6］Beggs D H，Brill J P.A study of two-phase flow in inclined pipes［J］.Journal of Petroleum technology，1973，25(05):607－617.

［7］Hagedorn A R，Brown K E.Experimental study of pressure gradients occurring during continuous two-phase flow in small-diameter vertical conduits［J］.Journal of Petroleum Technology，1965，17(04):475－484.

［8］Ros N C J.Simultaneous flow of gas and liquid as encountered in well tubing［J］.Journal of Petroleum Technology，1961，13(10):1037－1049.

［9］Duns Jr H，Ros N C J.Vertical flow of gas and liquid mixtures in wells［C］//6th World Petroleum Congress.World Petroleum Congress.USA: ［s.n.］，1963:451－465.

［10］Taitel Y，Dukler A E.A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow［J］.AIChE Journal，1976，22(1):47－55.

［11］Lin P Y，Hanratty T J.Prediction of the initiation of slugs with linear stability theory［J］.International journal of multiphase flow，1986，12(1):79－98.

［12］Wu H L，Pots B F M，Hollenberg J F，et al.Flow pattern transitions in two-phase gas/condensate flow at high pressure in an 8－ inch horizontal pipe［C］//Proc.BHRA Conf.，The Hague.The Netherlands:［s.n.］.1987:13－21.