A survey on cross-discipline of control and game

Daizhan CHENG,Ting LIU

Key Laboratory of Systems and Control,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China

Received 13 August 2015;revised 14 Septembr 2015;accepted 15 Septembr 2015

A survey on cross-discipline of control and game

Daizhan CHENG†,Ting LIU

Key Laboratory of Systems and Control,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China

Received 13 August 2015;revised 14 Septembr 2015;accepted 15 Septembr 2015

In recentyears,the cross discipline ofgame theory and the controltheory has been emerging.This paperwill survey this newly growing direction.First,the development from optimization of control systems to games consisting of multi-purpose controls is introduced,which demonstrates the close relationship between control theory and game theory.Secondly,the control-oriented game is considered.Three kinds of problems are discussed in details:i)Learning strategy in game theory,which is basically the same as the adaptive control;ii)state space approach for controlsystemsis applied to evolutionary games;and iii)machine-human game is treated as the optimal control problem.Finally,after introducing some new results on potential games,the game-based control is studied.Three kind of control problems using potential games are investigated:i)The consensus of multi-agent systems is considered;ii)the maximization of the distributed coverage of multi-agents on a graph is discussed;and iii)the congestion control is investigated using congestion game technology.Some other game-based control problems are also briefly introduced.A prediction for the control systems in next generation is presented in conclusion.

Control-oriented game,game-based control,evolutionary game,potential game,logical-Newtonian control system

DOI 10.1007/s11768-015-5086-2

1 Introduction

The technique of automation has a long history.In ancient China,there were numerous inventions including countless automatic machines and equipments.Among them are the seismograph(78-139 BC)for detecting earthquakes;the south-pointing chariot(850-330 AD),which is able to automatically point to a fixed direction when moving;and air pump machine powered by hydro-energy formetallurgy(25-57 BC).There were also many automatic devices world wide in old days.The most famous one could be the Watt speed regulator for steam engine,which was invented by J.Watt in 1768.However,it is commonly recognized that the Wiener’s famous book[1]is the symbol of the birth of control theory.

Similarly,games have also been exercised and investigated for long time.In China there is a famous storyabout the Tian Ji horse racing.The property allocation law in old Judaism’s rule “Talmud”is an example of cooperative game.However,also the von Neumann and Morgenstern’s book[2]is widely considered as the beginning of game theory.

Both control theory and game theory were born right after the World War II,partly because of the demand of war for control certain objects in certain competitions.Control and game have many characteristics in common.However,they have been developed independently on their own tracks,and have formed two independent branches of applied mathematics.Roughly speaking,the major common point for controland game is:the player or controller want to “manipulate”the object to reach their purpose.The major difference is:for control the object is something like machine,which is not intelligent,while for game the object is intelligent,which may anti-control.Hence,for control the purpose is to reach an optimization while for game only a Nash equilibrium,as a compromised optimization,may be reached.

Recently,after many years’development,people found that these two disciplines have closed insight relationship:tools and results in one branch can be used to the other branch.Hence a cross-discipline between them is emerging.It could be either a game-based control or a control-oriented game theory.The purpose of the survey is to introduce this new growing direction for control guys.

It was pointed out in AFOSR(Air Force Office of Scientific Research)[3]that“Next-generation systems will combine logical operations(such as symbolic reasoning and decision making)with continuous quantities(such as voltages,positions,and concentrations).”.It seems that next-generation of control systems consist of a control component and a decision making component.Recently developed cyber-physical systems could be of this type of systems[4].The game theory could be the foundation of reasoning and decision making.That is the motivation and the attempt of this paper.

The rest of this paper is organized as follows:Section 2 introduces the development from optimal control to game.The application of results in control theory to games is discussed in Section 3.Conversely,the application ofgame approach to controlproblems is introduced in Section 4.Section 5 is a brief concluding remark.

2 Optimal control vs.game theory

2.1 Game theory

Since the readers of this paper are assumed to be control guys,we give a brief introduction to game theory.We refer to[5,6]as an introduction to game theory.

Classical game theory consists of two parts:i)noncooperative game and ii)cooperative game.

Def i nition 1A normal non-cooperative game is a tripleG=(N,S,c),where

i)N={1,2,...,n}is the set of players.That is,in this game there arenplayers named as 1,2,...,n.

iii)cj(s):S→R is called the payoff function of playerj,which means how much playerjcan get from the game,j=1,...,n.Putting them together,we havec={c1,...,cn}.

For non-cooperative games,the Nash equilibrium is the most important concept,which is considered as the“solution”to non-cooperative games.It is defined as follows.

Def i nition 2In a normal gameG,a profiles=(x＊1,...,x＊n)∈S is called a Nash equilibrium if

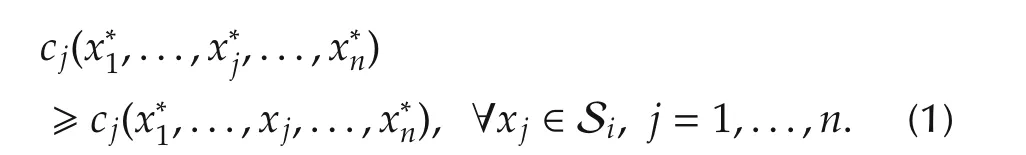
Example 1Consider a gameGwith two players:P1andP2:

▪Strategies ofP1:D2={1,2};

▪Strategies ofP2:D3={1,2,3}.

The payoffs are shown in Table 1,which is called the payoff bi-matrix,where the first(second)number at(i,j)shows the payoff ofP1(P2)whenP1andP2take strategiesiandj,respectively.

Table 1 Payoff bi-matrix.

It is easy to verify that the only Nash equilibrium is(1,2).

Next,we briefly introduce the cooperative game.

Def i nition 3A (transferable utility)cooperative gameG=(N,v)consists of

i)nplayersN:={1,...,n};

ii)v:2N→R is called the characteristic function;S∈2Nis called a coalition;v(S)is the value ofS,(which means the profit(cost:c:2N→R)of coalitionS)and

Example 2Consider a gameGwithN={1,2,...,n}:

LetS∈2N.A singe glove is worthy$0.01,a pair of gloves is worthy$1.Then,

The most important issue for cooperative games is:how to distribute the bonus achieved by the cooperation?It is defined as imputation.

Def i nition 4Given a cooperative gameG=(N,v),x∈Rnis called an imputation,if

2.2 Multi-objective control and game

We start from a simple control system as follows:

The problem is to find a control,which minimizesJ:

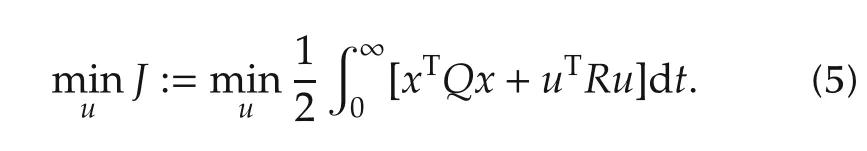
It is well known that the optimal control is

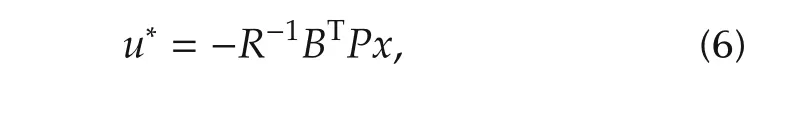
whereP≥0 satisfying algebraic Riccati equation:

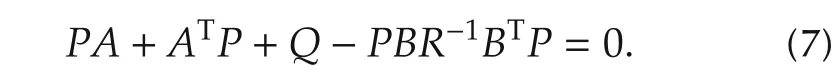
Next,we consider another linear system

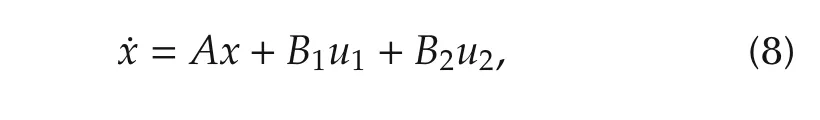
whereuiis to minimizeJi,i=1,2.That is,

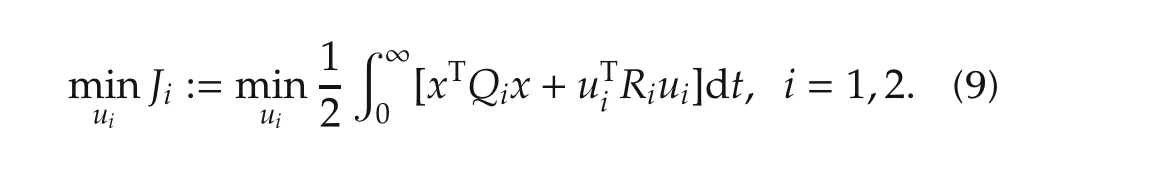
Then we get“optimal controls”,which satisfy the following equations:

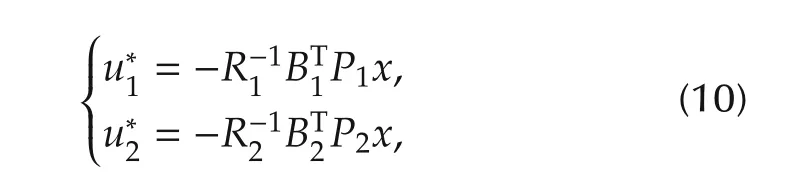
wherePi＞0,i=1,2,satisfying coupled algebraic Riccati equations:

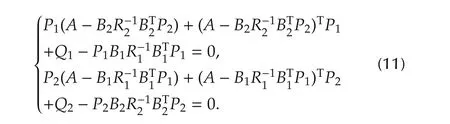
In fact,the “optimal controls”form a Nash equilibrium[7].

Consider an affine nonlinear control system

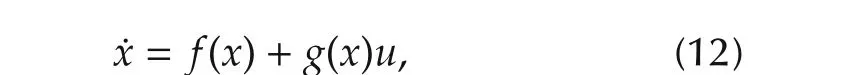
wherex(t)∈Rn,u(t)∈Rm,and assume the performance index is

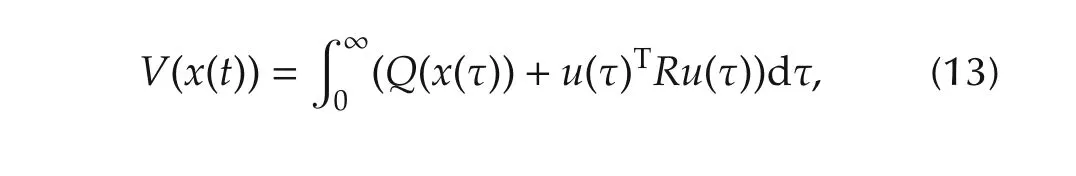
withQ(x)＞0,R＞0.Then the optimal control is

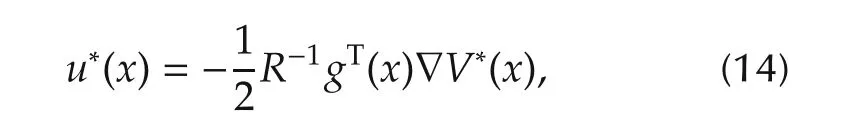
whereV＊(x)satisfies the following Hamilton-Jacobi-Bellman(HJB)equation:

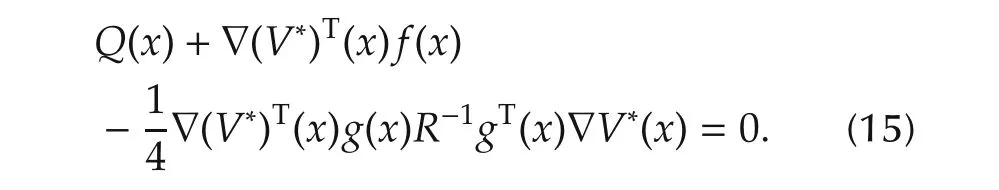
We refer to[8,9]for detailed discussion.

Similarto linearcase,when we considera multi-group input nonlinear system

wherex(t)∈Rn,uj∈Rmj,j=1,...,s.Moreover,the purpose ofujis to minimizeJj,that is

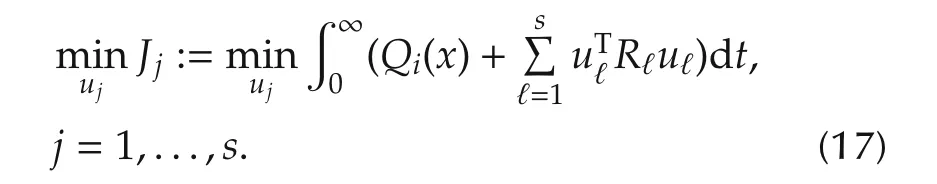
Then the “optimal solution”,which is again a Nash equilibrium,is[10]

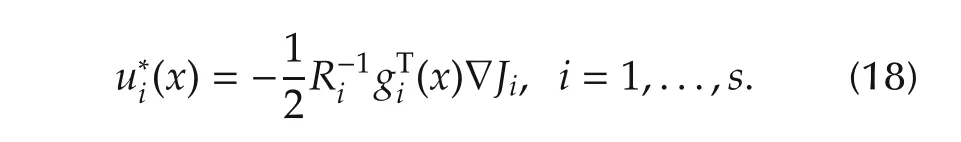
whereJi,i=1,...,ssatisfies the coupled HJB equation:

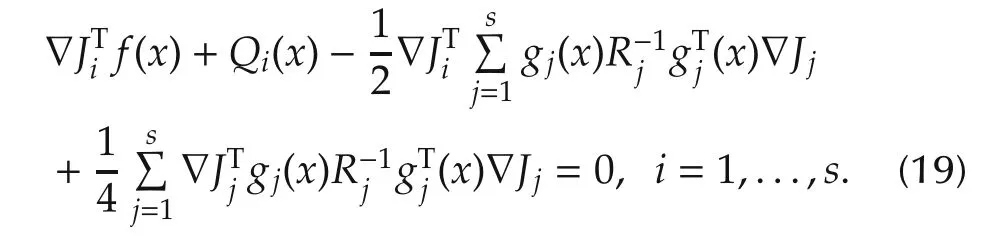
From the above discussion one sees easily that the control problems and the game problems are so closely related.Hence,the technique developed in one field can easily be used to the other.

This approach may be useful for practical multiobjective control problems,which have no natural corresponding relation between the set of controls and the set of objects.An artificial correspondence may need to be designed.

3 Control-oriented games

In this section,we consider some typical applications of tools in control theory to games.

3.1 Learning strategies

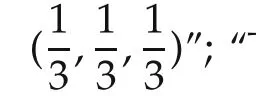
As demonstrated in[13],as well as in[12],learning strategy is a way to win in a competitive game.We refer to[14]for more about learning in games.In principle,updating the strategy through learning is the same as the adaptive control.We use an example to depict it.

Example 3Consider the R-P-S game.We describe the(simplest)learning strategy as follows:Assume thatP1uses the learning strategy.He sets an initial frequency for his opponent asF(0)=(fr(0),fp(0),fs(0))＞0,say,F(0)=(fr(0),fp(0),fs(0))=(1,1,1).

Then at stepthe updates his opponent’s frequency by

wherexi(t)is the strategy of playeriat stept.Then he uses

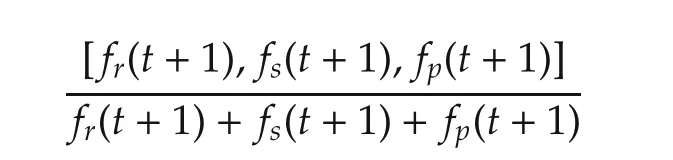
as the estimated mixed strategy,x2(t+1),ofP2att+1 and finds the best response to this strategy.That is

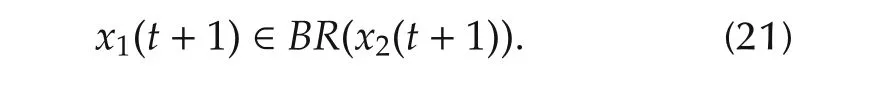
Itwasproved thatundercertain condition the learning strategy will converge to a Nash equilibrium[15].

3.2 State space frame for networked evolutionary games

State space representation is one of the most important tools in control theory.In this section,the algebraic state space representation is introduced and applied to networked evolutionary games.

Def i nition 5[16] A networked evolutionary game,denoted by((N,E),G,Π),consists of

i)a network(graph)(N,E);

ii)an FNG(fundamental network game),G,such that if(i,j)∈E,theniandjplay FNG with strategiesxi(t)andxj(t),respectively;

iii)a local information based strategy updating rule(SUR),Π.

There are two formulas to calculate the overall payoff for each player.

Def i nition 6[16] Letcijbe the payoff of the playeriin the FNG betweeniandj,then the overall payoff of playeriis

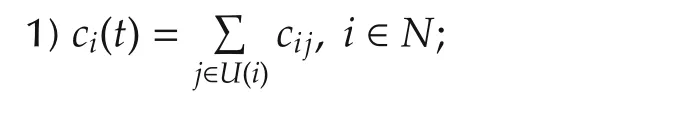
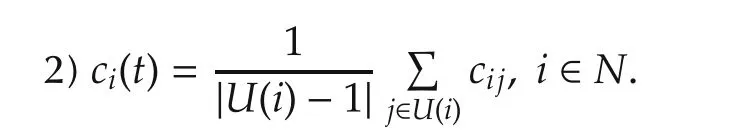
Assume that playeriuses his neighbors’information at timet,that is,their strategiesxj(t)and their payoffscj(t),j∈U(i)to update his strategy.That is

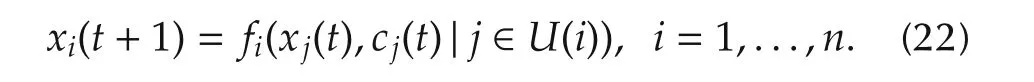
Sincecj(t)depends onxℓ(t),ℓ∈U(j),then we have

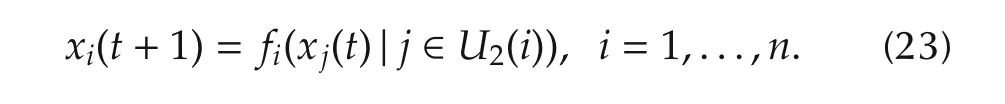
Note thatU2(i)is the set of neighborhood plus neighborhoods’neighborhood.

For finite games,(23)is a standardk-valued logical dynamic system.Therefore,the algebraic state space representation of logical systems is applicable[17].We use an example to depict this.

Example 4Consider a NEG,where the network isR3as Fig.1,the FNG is the R-S-P game and the payoff bi-matrix is show in Table 2.

Fig.1 R3.

Assume thatthe strategy updating rule isΠ-I(unconditional imitation with fixed priority),which is described as follows:

Table 2 Payoff bi-matrix of R-S-P.

In non-unique case:

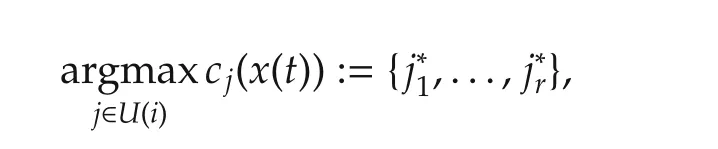
set priority:

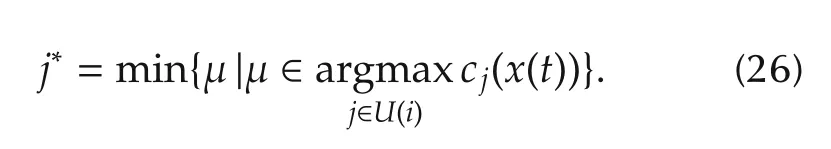
Then we have the dynamics described in Table 3.

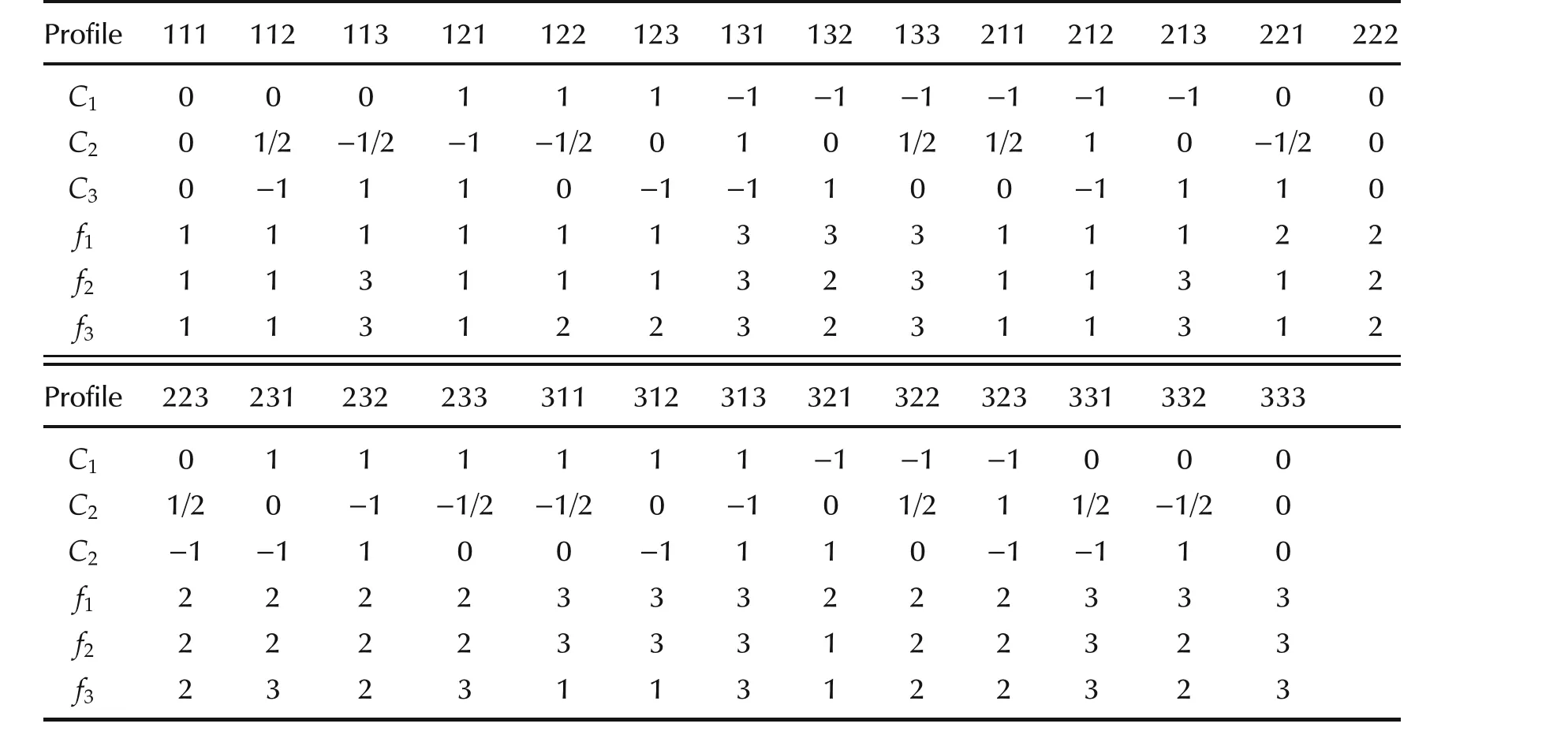
Table 3 Payoffs→Dynamics.

Identifying 1∼ δ13,2∼ δ23,3∼ δ33,we have the vector form of eachfias

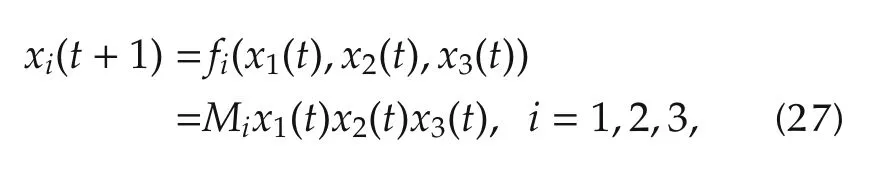
3.3 Man-machine games

Man-machine game is basically a controlproblem.Assume that there arenmachines andmhuman players.Their strategies are denoted bymi,i=1,...,nandhj,j=1,...,m,respectively.Then the dynamic model we concerned is described as follows:

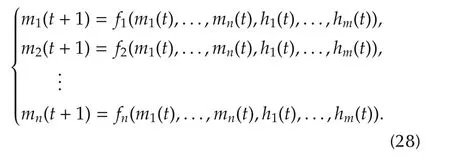
Assume that the human purpose is to maximize their payoff:

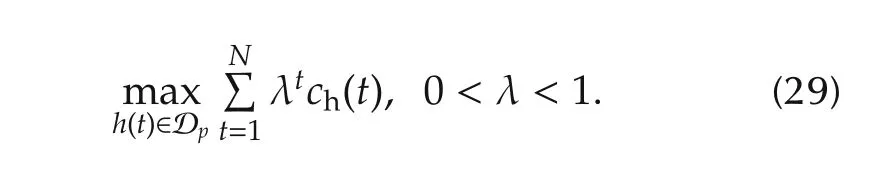
HereNcan be either finite or infinite.

Case 1Assume that both human’s and machine’s strategies are of pure strategy.Then we know the optimalsolution can appears on a cycle[18].Moreover,[19]shows that the optimal controls can be expressed as a state feedback form.The problem coincides with the optimization of logical control systems[20].

Case 2Assume that the mixed strategies are used.Then(28)becomes a probabilistic logical dynamic system and(29)is replaced by its expected values as

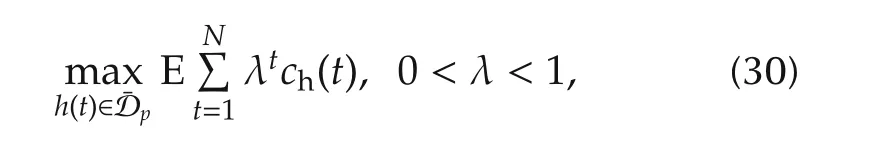
It is clear that the cycle searching technique is not applicable to it.Recently,[21]proposes a method to solve this problem.The approach consists of two steps.

Step 1Assume thatN＜∞.The dynamic programming is used to find the optimal control.

Step 2N= ∞:Choosing a proper filter length ℓ to get optimal control forN=ℓ.Then use the receding horizon method to get the optimal control for infinite case.

4 Game-based control

Since most of the game-based controls are related to potential games,we give a brief introduction to potential game first.

4.1 Potential games

Def i nition 7Consider a finite gameG=(N,S,c).Gis a potential game if there exists a functionP:S→R,called the potential function,such that for everyi∈Nand for everys-i∈S-iand∀x,y∈Si,

Potential games have some nice properties,which makes them helpful in control design.We listed some as follows.

Theorem 1[22] IfGis a potential game,then the potential functionPis unique up to a constant number.Precisely ifP1andP2are two potential functions ofG,thenP1-P2=c0∈R.

Theorem 2[22] Every finite potential game possesses a pure Nash equilibrium.The SUR:Sequential or cascading myopic best response adjustment(MBRA)leads to a Nash equilibrium.

Verifying whether a game is potential is a long standing problem[23,24].It was pointed in[24]that“It is not easy,however,to verify whether a given game is a potential game.”Recently,[25]presents an easy way to verify this.We briefly introduce this method.

Consider a normal game(N,S,c),where|N|=n,|Si|=k,i=1,...,n,and the payoff function of playeriis denoted as

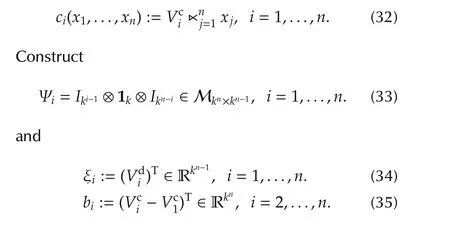
Finally,we construct a linear system as

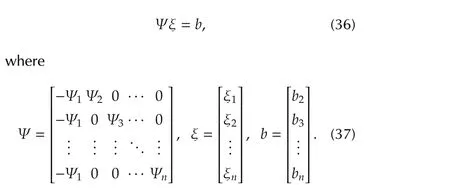
(36)is called the potential equation and Ψ is called the potential matrix.Then we have the following result:

Theorem 3[25] A finite gameGis potential if and only if the potential equation has solution.Moreover,the potentialPcan be calculated by

4.2 Consensus of MAS

Consider a multi-agent system[26].Assume that the network graph is(N,E(t)),whereN={1,2,...,n}are agents and they have a time-varying topology:E(t).The dynamic model is

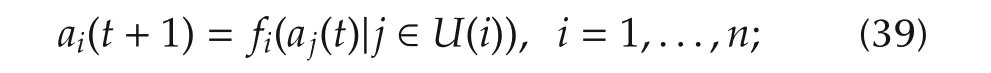
and the set of strategies are

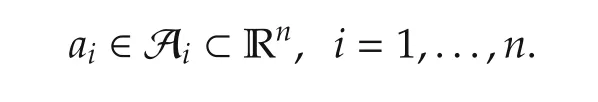
Define a potential function as

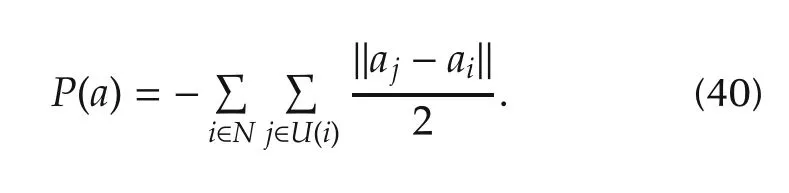
Correspondingly,the payoff functions are designed as

Then it is clear that asP(a)reaches its maximum the MAS also reaches a consensus.An algorithm called binary log-linear learning(BLLL)is introduced in[26].Two assumptions are given as

A1)Reversibility:Fora1i,a2i∈Ai,

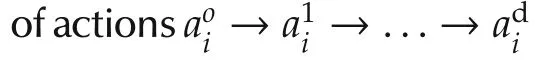
Then we have the following result:

Theorem 4[26]Consider system(39).Assume A1)and A2),then BLLL leads to a consensus.

Consensus via strategy reinforced learning has also been discussed in[27].

4.3 Distributed coverage of graphs

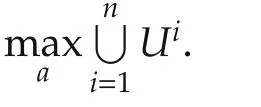
The problem can also be formulated as a potential game.we define the potential function as

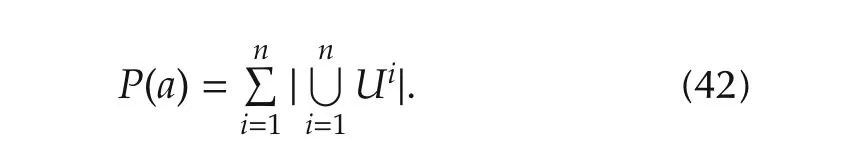
The corresponding payoff functions are designed as

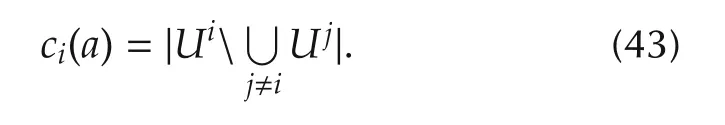
Denote the restricted action set asRi(ai(t-1))⊂V.

Give the region condition as

▪Covering radiusdj(If ξ ∈Udj(j),then ξ is covered byj).

For the computation ofci(a′i,a-i(t))wherea′i∈Ai(ai(t)),the following condition just satisfied:

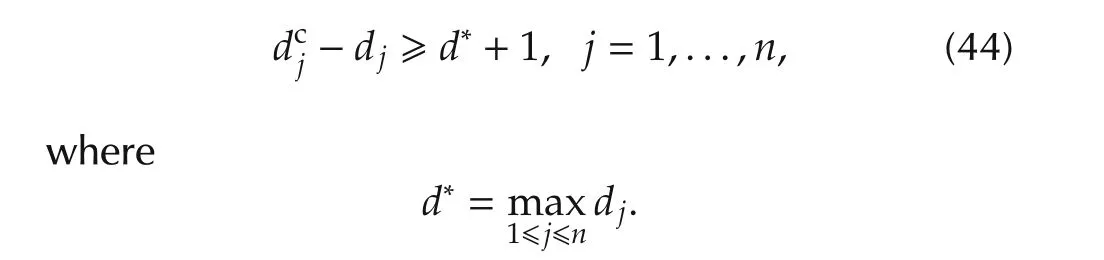
Then we have the following theorem.

Theorem5[28]Assuming A1),A2),and(44)and using the BLLL algorithm(with large enough β),the number of covered nodes is asymptotically maximized(in probability).

4.4 Congestion games

Congestion game is also called the congestion control in control theory.We use an example to depict it.

Example 5[22]Consider the road map as Fig.2.Assume that there are two players:Player 1 wants to go fromAtoC,player 2 wants to go fromBtoD:

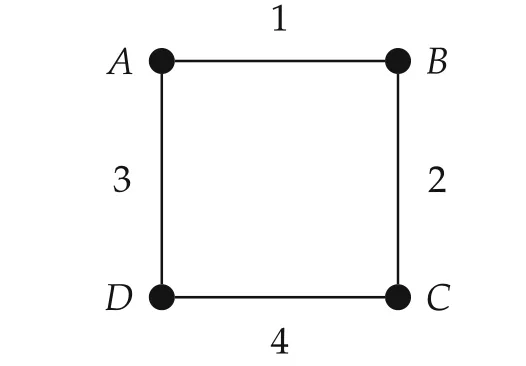
Fig.2 A road map.

Then player 1 has the set of strategies as

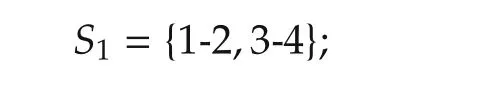
and player 2 has the set of strategies as

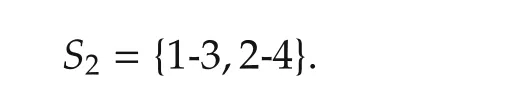
Assume that the cost for roadjto be used byscars is denoted bycj(s).Then the payoff bi-matrix is obtained as in Table 3.

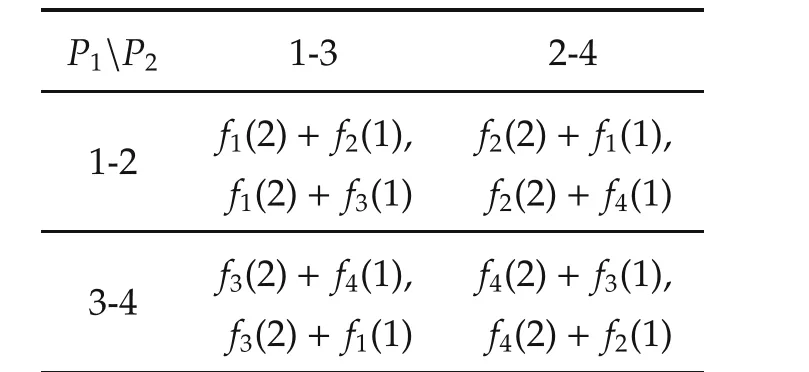
Table 3 Payoff bi-matrix of roads.

It is easy to verify that this is a potential game with

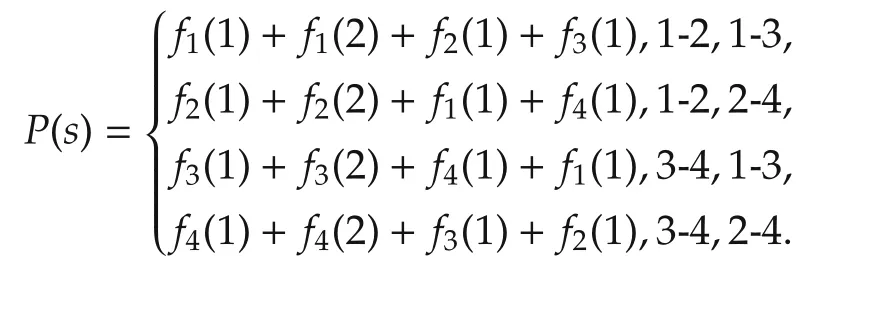
In general,a congestion model can be described as follows:

Def i nition 8A congestion model is defined as follows:

where

▪Players:N={1,2,...,n};

▪Facilities:M={1,2,...,m};

▪Set of strategies:Si:= Σi⊂ 2M;

▪Facility cost:fj:N→R(depends on number of users).

LetAi∈ Σibe a strategy.

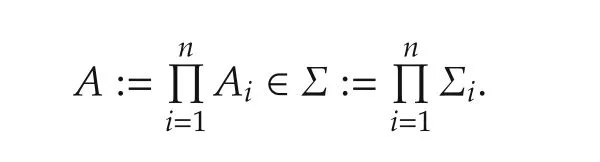
For eachj∈M,set

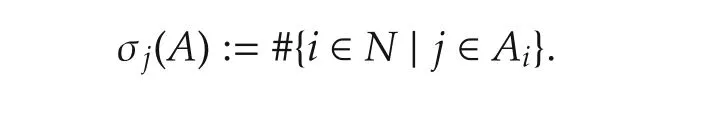
Then we define

▪Payoff functions:

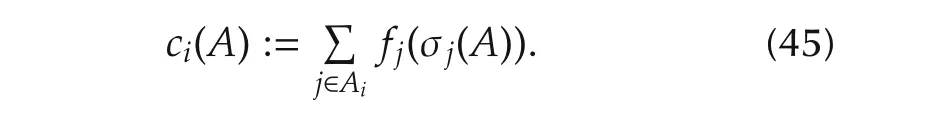
▪Potential function:

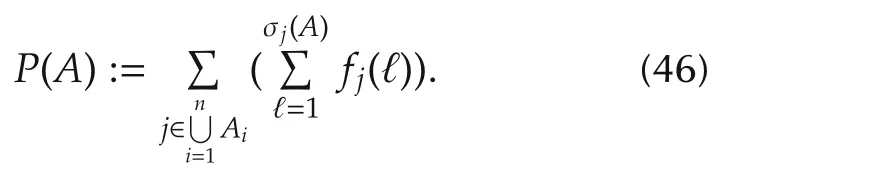
The following theorems show that the congestion game is essentially equivalent to a potential game:

Theorem 6[22]Every congestion game is a potential game.

Theorem 7[22] Every finite potential game is isomorphic to a congestion game.

Congestion game technique hasbeen used to the road control[26,30].It seems also useful for some other control problems.

4.5 Some other applications

What we discussed above are some potential game based applications.There are many other applications of game theory to control problems.They involve various topics in game theory.Some examples are:

▪the scheduling-allocation of power systems[31,32];and

▪the application ofcooperative game theory to control problems[33].

There are also many new results about game-based controls in recent TAC,for instance,[34],[35]and[36],just to name few.

5 Conclusions

Game theory and control theory are deeply interconnected.Their cross-discipline is a very attractive new growing direction of control theory.In this survey paper we first discussed the development from optimal control to the games led from multi-purpose controls.Then we discussed the two directions of interactions.

1)Control theory→Game theory:

▪state space approach to evolutionary games;

▪man-machine games;and

▪learning(or adaptive)control in games.

2)Game theory→Control theory(potential):

▪control of MASs via designed potentials;

▪distributed graph covering;

▪congestion control;and

▪control of power systems,etc.

It was mentioned in[3]that“Among the challenges currently facing the field,a few examples provide insight into the difficulties ahead:Control of systems with both symbolic and continuous dynamics:Next-generation systems will combine logical operations(such as symbolic reasoning and decision making)with continuous quantities(such as voltages,positions,and concentrations).The current theory is not well tuned for dealing with such systems,especially as we scale to very large systems.”.It seems very likely that the control system of next generation should consist of two parts:Logical part and mechanical part,which may be called a logical-Newtonian control system(LNCS).In an LNCS the mechanical part is the traditional control system and the logical part is the decision-making part,and the game theory willplay a key role forthis.Briefly,we may expect that the control system of next generation is a combination of dynamic game with mechanical control system.

[1]N.Wiener.Cybernetics:Or Control and Communication in the Animal and the Machine.Paris:Hermann&Cie,Cambridge,MA:MIT Press,1948.

[2]J.von Neumann,O.Morgenstern.Theory ofGames and Economic Behavior.Princeton,NJ:Princeton University Press,1944.

[3]R.M.Murray,K.M.Astrom,S.P.Boyd,et al.Future directions in control in an information rich world-A summary of the report of the panel,on future directions in control,dynamics,and systems.IEEE Control Systems Magazine,2003,23(2):20-33.

[4]R.Baheti,H.Gill.Cyber-physical systems.The Impact of Control Technology,Washington D.C.:IEEE,2011:161-166.

[5]R.Gibbons.A Primer in Game Theory.Harlow:Printice Hall,1992.

[6]Z.Xie.An Introduction to Game Theory.Beijing:Science Press,2010(in Chinese).

[7]J.C.Engwerda.Computational aspects of the open-loop Nash equilibrium in linear quadratic games.Journal of Economic Dynamics and Control,1998,22(8/9):1487-1506.

[8]A.Friedman.Differential Games.Rhode Island:American Mathematical Society,1974.

[9]N.Yu.Lukoyanov.A Hamilton-Jacobi type equation in control problems with hereditary information.Journal of Applied Mathematics and Mechanics,2000,64(2):243-253.

[10]F.L.Lewis,D.L.Vrabie,V.L.Syrmos.Optimal Control.3rd ed.Hoboken,NJ:John Wiley&Sons,2012.

[11]O.Candogan,I.Menache,A.Ozdaglar,et al.Flows and decompositions of games:harmonic and potential game.Mathematics of Operations Research,2011,36(3):474-503.

[12]Z.Wang,B.Xu,H.Zhou.Socialcycling and conditional responses in the Rock-Paper-Scissors game.Scientific Reports,2014:DOI 10.1038/srep05830.

[13]V.Mnih,K.Kavukcuoglu,D.Silver,et al.Human-level control through deep reinforcement learning.Nature,2015,518(7540):529-533.

[14]D.Fudenberg,D.K.Levine.The Theory of Learning in Games.Cambridge:The MIT Press,1998.

[15]D.Monderer,L.S.Shapley.Fictitious play property for games with identical interests.Journal of Economic Theory,1996,68:258-265.

[16]D.Cheng,F.He,H.Qi,et al.Modeling,analysis and control of networked evolutionary games.IEEE Transactions on Automatic Control,2015,60(9):2402-2415.

[17]D.Cheng,H.Qi,Z.Li.Analysis and Control of Boolean Networks:A Semi-tensor Product Approach.London:Springer,2011.

[18]Y.Mu,L.Guo.Optimization and identification in nonequilibrium dynamical games.Proceedings of the 48th IEEE Conference on Decision and Control,Shanghai:IEEE,2009:5750-5755.

[19]Y.Zhao,Z.Li,D.Cheng.Optimal control of logical control notworks.IEEE Transactions on Automatic Control,2011,56(8):1766-1776.

[20]E.Fornasini,M.E.Valcher.Optimal control of Boolean control systems.IEEE Transactions on Automatic Control,2014,59(5):1258-1270.

[21]D.Cheng,Y.Zhao,T.Xu.Receding horizon based feedback optimization for mix-valued logical networks.IEEE Transactions on Automatic Control,2015:DOI 10.1109/TAC.2015.2419874.

[22]D.Monderer,L.S.Shapley.Potential games.Games and Economic Behavior,1996,14(1):124-143.

[23]J.Hofbauer,G.Sorger.A differential game approach to evolutionary equilibrium selection.International Game Theory Review,2002,4(1):17-31.

[24]Y.Hino.An improved algorithm for detecting potential games.International Journal of Game Theory,2011,40(1):199-205.

[25]D.Cheng.On finite potential games.Automatica,2014,50(7):1793-1801.

[26]J.R.Marden,G.Arslan,J.S.Shamma.Cooperative control and potential games.IEEE Transactions on Systems Man and Cybernetics-Part B:Cybernetics,2009,39(6):1393-1407.

[27]M.I.Abouheaf,F.L.Lewis,M.S.Mahmoud,et al.Discrete-time dynamic graphical games:model-free reinforcement learning solution.Control Theory and Technology,2015,13(1):55-69.

[28]A.Y.Yazicioglu,M.Egerstedt,J.S.Shamma.A game theoretic approach to distributed coverage of graphs by heterogeneous mobile agents.Estimation and Control of Networked Systems,2013,4:309-315.

[29]M.Zhu,S.Martinez.Distributed coverage games for energyaware mobile sensor networks.SIAM Journal on Control and Optimization,2013,51(1):1-27.

[30]X.Wang,N.Xiao,T.Wongpiromsarn,et al.Distributed consensus in noncooperative congestion games:an application to road pricing.IEEE International Conference on Control and Automation,Hangzhou:IEEE,2013:1668-1673.

[31]T.Heikkinen.A potential game approach to distributed power control and scheduling.Computer Networks,2006,50(13):2295-2311.

[32]R.Bhakar,V.S.Sriram,N.P.Padhy,et al.Probabilistic game approaches for network cost allocation.IEEE Transactions on Power Systems,2010,25(1):51-58.

[33]A.Nedic,D.Bauso.Dynamic coalitional TU gemes:distributed bargaining among players’neighbors.IEEE Transactions on Automatic Control,2013,58(6):1363-1376.

[34]G.Arslan,M.F.Demirkol,S.Yuksel.On games with coupled constraineds.IEEE Transactions on Automatic Control,2015,60(2):358-372.

[35]A.Cortes,S.Martinez.Self-triggered best-response dynamics for continuous games.IEEETransactionson AutomaticControl,2015,60(4):1115-1120.

[36]T.Mylvaganam,M.Sassano,A.Astolfi.Constructive e-Nash equilibria for nonzero-sum differatial games.IEEE Transactionson Automatic Control,2015,60(4):950-965.

the Ph.D.degree from Washington University,St.Louis,in 1985.Since 1990,he is a professor with Institute of Systems Science,Chinese Academy of Sciences.His research interests include nonlinear system control,numerical method in system analysis and control,and game theory.E-mail:dcheng@iss.ac.cn.

TingLIUreceived the B.S.degree from Xi’an University of Science and Technology in 2011.Currently,he was a Ph.D.candidate at Academy of Mathematics and Systems Science,Chinese Academy of Sciences.His research interests include game theory and complex system.E-mail:tliu@amss.ac.cn.———-

†Corresponding author.

E-mail:dcheng@iss.ac.cn.Tel.+86-10-8254 1232;fax:+86-10-6258 7343.

This work was supported by the National Natural Science Foundation of China(Nos.61074114,61273013).

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg