Stochastic sub-gradient algorithm for distributed optimization with random sleep scheme

Peng YI,Yiguang HONG

Key Lab of Systems and Control,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China

Received 10 October 2015;revised 27 October 2015;accepted 27 October 2015

Stochastic sub-gradient algorithm for distributed optimization with random sleep scheme

Peng YI,Yiguang HONG†

Key Lab of Systems and Control,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China

Received 10 October 2015;revised 27 October 2015;accepted 27 October 2015

In thispaper,we considera distributed convex optimization problem ofa multi-agentsystem with the globalobjective function as the sum of agents’individual objective functions.To solve such an optimization problem,we propose a distributed stochastic sub-gradient algorithm with random sleep scheme.In the random sleep scheme,each agent independently and randomly decides whether to inquire the sub-gradient information of its local objective function at each iteration.The algorithm not only generalizes distributed algorithms with variable working nodes and multi-step consensus-based algorithms,but also extends some existing randomized convex set intersection results.We investigate the algorithm convergence properties under two types of stepsizes:the randomized diminishing stepsize that is heterogeneous and calculated by individual agent,and the fixed stepsize that is homogeneous.Then we prove that the estimates of the agents reach consensus almost surely and in mean,and the consensus point is the optimal solution with probability 1,both under randomized stepsize.Moreover,we analyze the algorithm error bound under fixed homogeneous stepsize,and also show how the errors depend on the fixed stepsize and update rates.

Distributed optimization,sub-gradient algorithm,random sleep,multi-agent systems,randomized algorithm

DOI 10.1007/s11768-015-5100-8

1 Introduction

Recent years have witnessed growing research attention in distributed optimization and control,due to a broad range of applications such as distributed parameter estimation in sensor networks,resource allocation in communication systems,and optimal power flow in smart grids in[1-7].Many complicated practical problems can be formulated as distributed optimization problems with a global objective function as the sum of agents’individual objective functions,where the individual function of each agent cannot be known or manipulated by other agents.Various significant distributed optimization algorithms have been proposed and analyzed,including primal domain(sub)gradient algorithms[1,2,6,8-11],dual domain algorithms[12],and primal-dual domain algorithms[5,7,13-15].

Distributed optimization problems arise in network decision problems with information distributed through the agents over the network.Hence,each agent can only obtain the(sub)gradient of its local objective function at any given testing point by manipulating its own private data.However,the calculation of(sub)gradient may involve computation with big data[16],or solving certain subproblem[17],or calculating multiple function values[18],which is still a big computation burden for each agent.Moreover,in application cases,like[19]and[20],each agent needs to perform measurements or observations for gradient information,which results in additional energy burden.Therefore,it might be undesirable to inquire local gradient information at each iteration.In fact,for the convex set intersection problem,which is a specific case of distributed optimization with the localobjective function as the distance to a local convex set,[21]and[22]have introduced random sleep scheme into projection-based consensus algorithms and shown its convergence and efficiency.

On the otherhand,itmightbe inefficientto inquire the local gradient information at each iteration.Due to data distributiveness,the agents’estimates of the optimal solution cannot keep consensus all the time.To eliminate the disagreements between the agents’estimates,which indeed constitute the main obstacle in the optimal solution seeking,consensus-type algorithms are usually incorporated into the distributed optimization algorithms,like[1-15].Recently,[23]proposed a distributed algorithm to preform multiple consensus steps before updating with gradients,in order to remarkably improve the algorithm convergence speed,but each agent is required to perform the same number of consensus steps before updating with gradients.

In this paper,we propose a distributed stochastic subgradient algorithm with random sleep scheme to solve a nonsmooth constrained convex optimization problem.In such algorithms,each agent first performs a consensus step by a convex combination of its own estimate and its neighbor agents’estimates in a uniformly jointly strongly connected communication network.Then each agent independently makes a Bernoulli experiment to decide whether it performs update step with its own objective function.It is called the waking agent if the agent performs update,or called the sleeping agent otherwise.The waking agents can calculate noisy subgradients at given testing point with local objective functions,and then update the estimates by moving along the noisy sub-gradient directions and projecting onto their feasible sets.Meanwhile,the sleeping agents only update their estimates with the consensus step information.

Different from existing algorithms[1-15],the agents in our design need not calculate sub-gradient information and perform projection at each iteration.Thus,the random sleep scheme works similarly with the ones in[21]and[22],and is introduced to reduce the computation and energy burden forthe problems with costly calculation of sub-gradient and projection.This scheme is also similar with the variable working nodes design in[24],whose numerical experience shows remarkable communication and computation burden reduction.Besides that,the random sleep scheme can be seen as the randomized generalization of the multi-step consensus based algorithm in[23]by allowing heterogeneous and randomized consensus steps.Furthermore,the random sleep scheme can model the random failure or scheduling of agents in uncertain environments[25,26].

The algorithm convergence analysis is given with two types of stepsizes.The randomized diminishing stepsize is taken as the inverse of gradient update times,which can be calculated by each agent in a distributed manner.With the randomized diminishing stepsize,we prove that all the agents reach consensus and the consensual point belongs to the optimal solution set with probability one.Then we investigate the algorithm error bounds when adopting the fixed stepsize α.In this case,the agents cannot find the precise optimal solution as proved in[11].Here,the distance between agents’estimates and the optimal solution is analyzed when the local objective functions are smooth strongly convex functions,and the optimal function value gap is given when the local objective functions are nonsmooth convex functions,both depending on stepsize α and update rates of the agents.

The contributions of this paper can be found in the following aspects:

▪Random sleep scheme is firstly proposed for distributed optimization.It generalizes the works of[21]and[22],which are special cases of the nonsmooth convex objective functions that we handle here,and moreover,it provides a randomized version of the multi-step consensus based algorithm in[23].

▪The algorithm convergence propertiesare fully investigated with both the randomized diminishing stepsize and fixed stepsize,which provide further understanding and insight of random sleep scheme in addition to[24].

The paper is organized as follows.The distributed optimization problem is first formulated,and then the distributed algorithm with random sleep scheme is proposed in Section 2.In Section 3,the algorithm convergence analysis is given under randomized diminishing stepsize.We first show that all the agents reach consensus in mean and almost surely,and then prove that all the agents converge to the same optimal solution with probability 1.The error bound is analyzed for the fixed stepsize case in Section 4.Numericalexamples are given to illustrate the algorithm performance in Section 5.Finally,the concluding remarks are presented in Section 6.

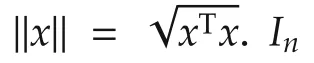
2 Problem formulation and distributed optimization algorithm

In this section,we first give the formulation of a distributed nonsmooth convex optimization problem with set constraint,and then propose a distributed optimization algorithm with random sleep scheme.

2.1 Problem formulation

Consider a group of agents with agent index set N={1,...,n}to cooperatively optimize the sum of their local objective functionsfi(x),that is,

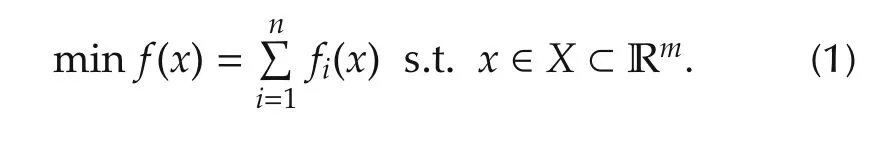
HereXis a nonempty convex set,which is also assumed to be closed and bounded.Eachfi(x)is a convex function over an open set containing the setX.Notice thatfi(x)is privately known by agenti,and cannot be shared or known by other agents.

We first give an assumption about problem(1).

Assumption 1The optimal solution set

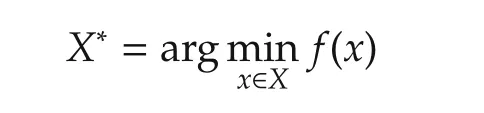
is nonempty.Moreover,the sub-gradient set of local objective functionsfi(x)is uniformly bounded over the compact setX,i.e.,

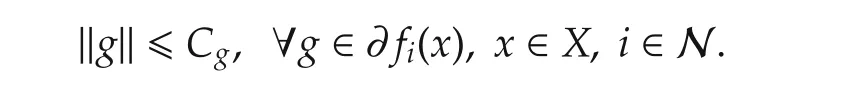
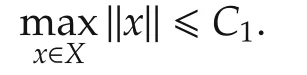
We call anyx＊∈X＊to be the optimal solution andf(x＊)to be the optimal value.It follows from[27]that,for any vectorg∈∂f(x),

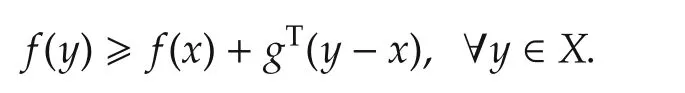
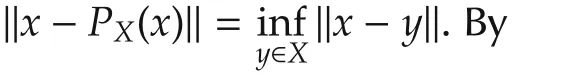
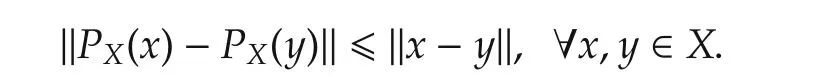
Without global information,the agents have to solve problem(1)by local computation and information sharing.The information sharing networks among the agents are usually represented by graphs,which may be timevarying due to link failures,packet dropouts,or energy saving schedule.Here the time-varying information sharing network is described by the graph sequence{G(k)=(N,ℇ(k)),k=1,2,...}with N representing the agent set and ℇ(k)containing all the information interconnections at timek.If agentican get information from agentjat timek,then(j,i)∈ ℇ(k)and agentjis said to be in agenti’s neighbor set Ni(k)={j|(j,i) ∈ ℇ(k)}.A path of graph G is a sequence of distinct agents in N such that any consecutive agents in the sequence corresponding to an edge of graph G.Agentjis said to be connected to agentiif there is a path fromjtoi.The graph G is said to be strongly connected if any two agents are connected.The following assumption about the sequence{G(k)=(N,ℇ(k)),k=1,2,...}can guarantee that any agent’s information can reach any other agents quite often in the long run.

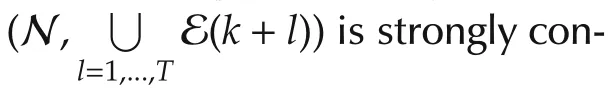
Define matricesA(k)=[aij(k)]according to graph G(k)withaij(k)＞0 ifj∈Ni(k)andaij(k)=0 otherwise.All matricesA(k)are double stochastic,namely,1TnA(k)=1TnandA(k)1n=1n.We also assume that there exists a constant τ∈(0,1)such that for any timek,aij(k)≥ τ whenj∈ Ni(k)andaii(k)≥ τ,∀i.Define Φ(k,s)=A(k)A(k-1)...A(s+1)for allk,swithk＞s≥ 0 and Φ(k,k)=In.Then the following lemma holds according to reference[1].

Lemma 1With Assumption 2 andA(k),Φ(k,s)defined as before,we obtain

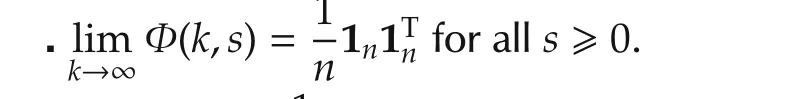
where

2.2 Distributed optimization algorithm with random sleep scheme

The agentihas an estimate ofx＊denoted asxi(k)with the randomly selected initial valuexi(0)∈X.Let χi,k,k≥ 0 be independent identically distributed(i.i.d.)Bernoulli random variables with P(χi,k=1)= γiand P(χi,k=0)=1- γi,0 ＜ γi＜ 1.Random variables χi,k,k≥ 0 are also assumed to be independent across the agents.The distributed optimization algorithm with random sleep scheme is given as follows:

Consensus:

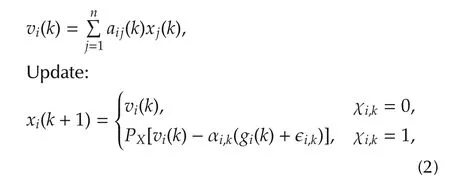
wheregi(k)+ϵi,kis one noisy sub-gradient offi(x)at pointvi(k)andgi(k)∈∂fi(vi(k)).In other words,the algorithm(2)solves the problem(1)with the following two steps at each iterationk.

▪Consensus step:The agentifirst gets its neighbors’estimates{xj(k),j∈Ni(k)}through the network G(k).Then agentimakes a convex combination ofxi(k)and{xj(k),j∈Ni(k)}with weightsaij(k),j=1,...,nto reachvi(k).

▪Update step:Agentidoes a Bernoulli experiment with random variable χi,k.When χi,k=1,agentiinquires its local objective functionfi(x)and gets the noisy sub-gradient directiongi(k)+ϵi,k,which is not separable.Then agentiupdates its estimate by moving alonggi(k)+ϵi,kwith stepsize αi,k,and then projects the result onto the constraint setX.With probability 1-γi,χi,k=0 and agentionly updates its estimate tovi(k).That is,γidecides the update rate of agenti.

Agenticannotgetthe exactsub-gradientdirection but only a noisy onegi(k)+ϵi,k,where ϵi,kis the sub-gradient observation noise at iterationk.Noisy subgradients may come from the gradient evaluation process or stochastic optimization problems(see[8-10]and[18]).

We introduce a random sleep scheme into the distributed optimization for the following three reasons:

i)The random sleep scheme wasintroduced to reduce the projection calculation in the convex set intersection problem in[22].Here it is introduced to reduce the calculation of sub-gradient and projection,especially when the objective functions have big data sets or involve subproblems.

ii)[23]proposed to perform multiple consensus steps before updating with gradients,and achieved fast convergence speed.In fact,the disagreement of the agents’estimates results in gradient evaluation errors,and therefore,it is preferred to reduce the disagreement by multiple consensus steps before gradient evaluations.Hence,the random sleep scheme can be regarded as the randomized version of the multi-step consensus based algorithm by allowing heterogeneous update rates.

iii)The random sleep scheme can model the random failure of multi-agent networks,especially in sensor networks(referring to[25]and[26]).

DenoteJkas the set of agents performing the update step at timek:Jk={i:χi,k=1}.LetFkbe the σ-algebra generated by the entire history of the algorithm up to timek,i.e.,fork≥1,

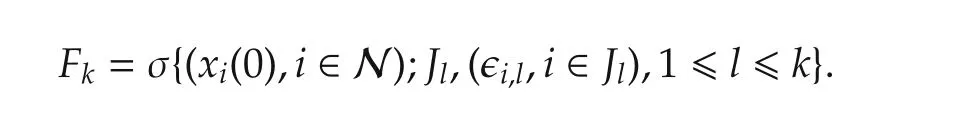
The following assumption imposed on the stochastic noise ϵi,khas been widely adopted[8,9].

Assumption 3There exists a deterministic constant ν＞0 such that

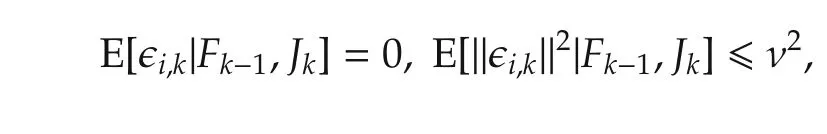
∀i∈N,k≥ 1 with probability 1.

The following two lemmas are very useful in the convergence analysis to achieve the optimization,which can be found in[28]and[27],respectively.

Lemma 2Suppose

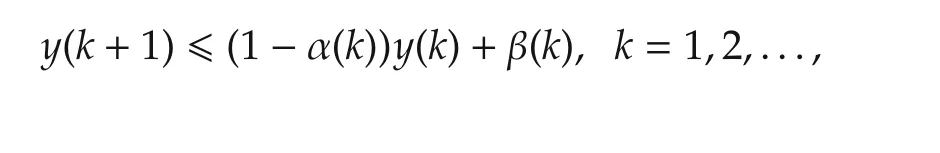
with 0＜ α(k)≤ 1,β(k)≥ 0,k=1,2,...Then

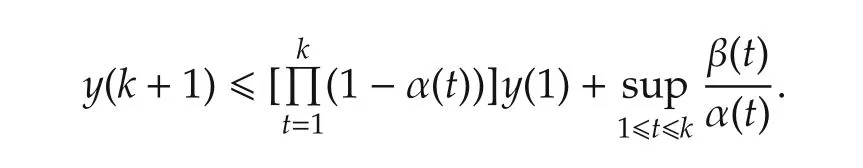
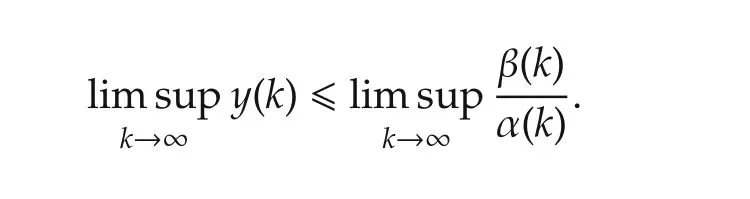
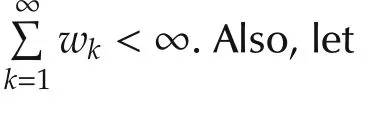
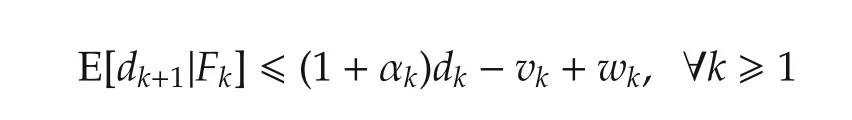
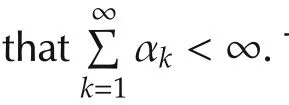
The stepsize αi,kin(2)determines how the agents update with the gradient information when the agents are waking,and hence,plays a key role in the algorithm performance.We will give the convergence analysis under randomized diminishing stepsize and the error bound analysis under fixed stepsize in Sections 3 and 4,respectively.

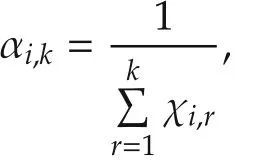
3 Convergence analysis with randomized diminishing stepsize

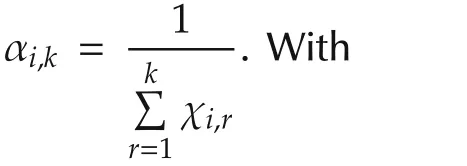
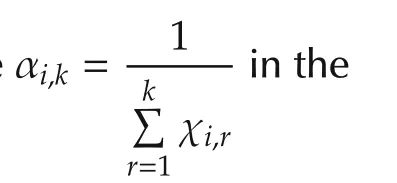
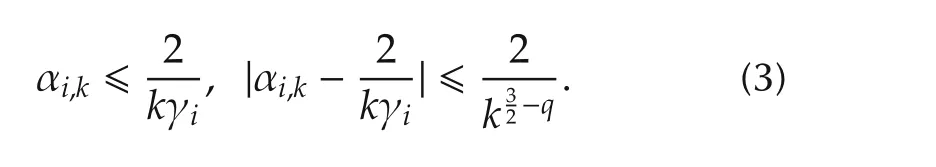
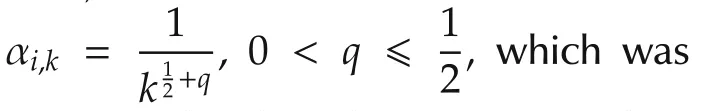
3.1 Consensus result

In this subsection,we first show that all the agents reach consensus in mean,and then show that all the agents also reach consensus with probability 1.Without loss of generality,we assume the dimensionmto be 1.

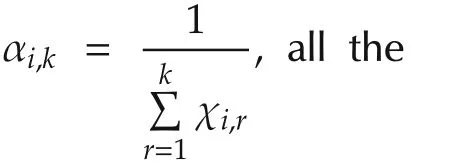
agents reach consensus in mean with algorithm(2),that is

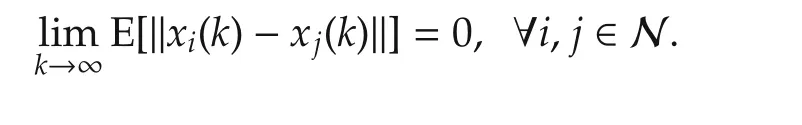
ProofDefineζi(k)=PX[vi(k)-αi,k(gi(k)+ϵi,k)]-vi(k)for agenti∈Jk,and ζi(k)=0 for agenti∉Jk.We rewrite

the dynamics of agentias follows:

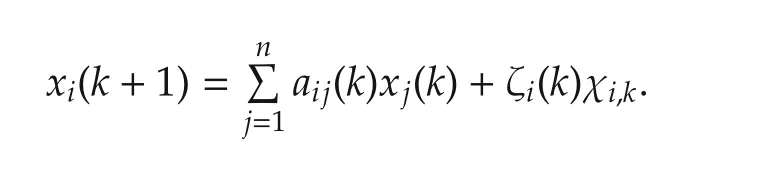
where the second step follows from Assumption 1,Lemma 1,equations(4)-(6)and E[E[x|F1]|F2]=E[x|F2]forF2⊂F1.

Hence,still with E[E[x|F1]|F2]=E[x|F2]forF2⊂F1and(6),fork＞s＞˜k,with probability 1,we have

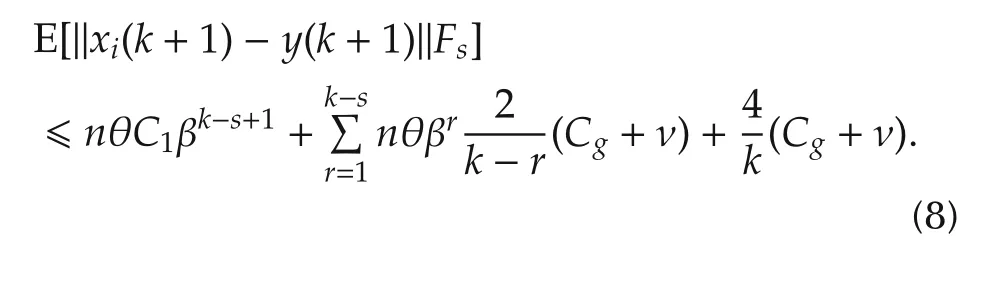
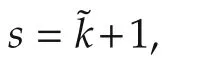
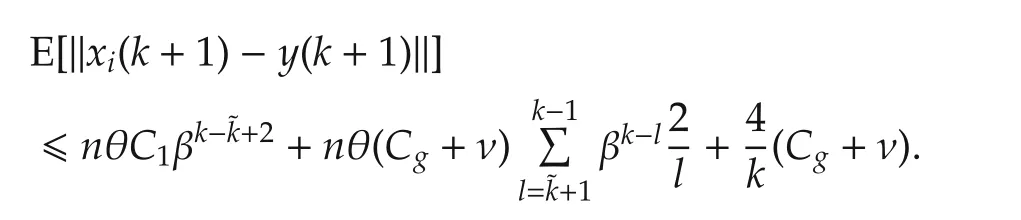
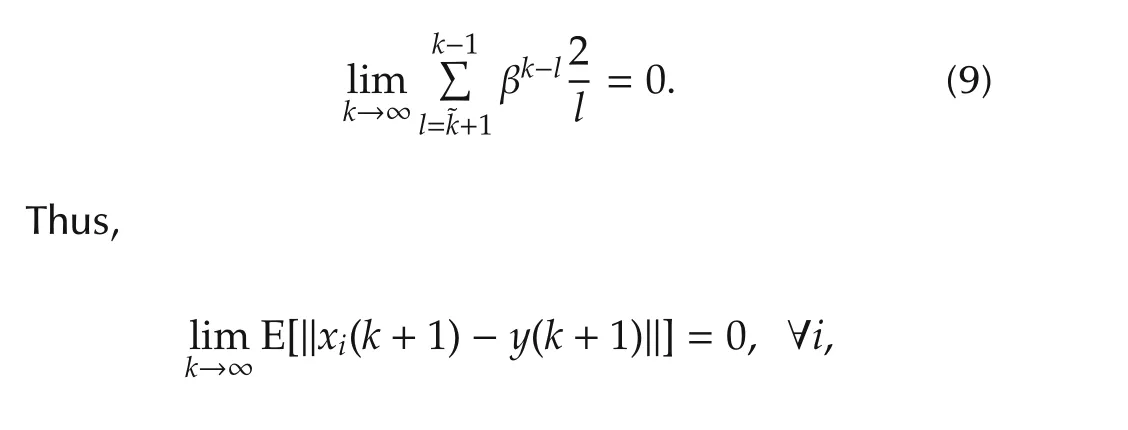
which implies that the agents reach consensus in mean. □

Next result describes the consensus rate and will be used in the following analysis.

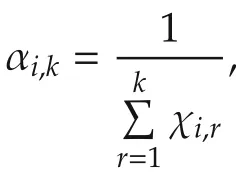
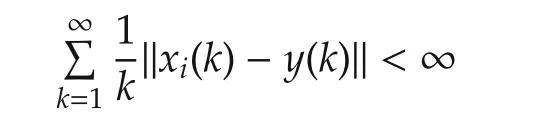
with probability 1 by algorithm(2).

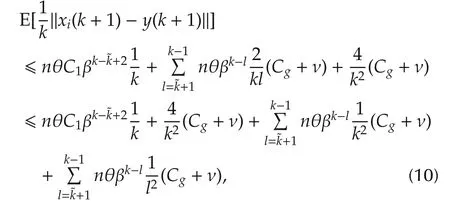
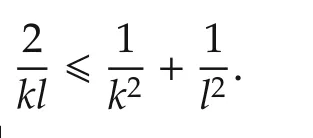
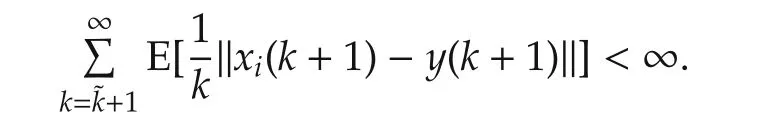
From the monotone convergence theorem(referring to[29]),

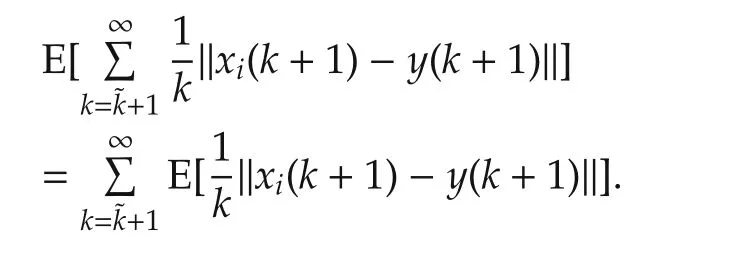
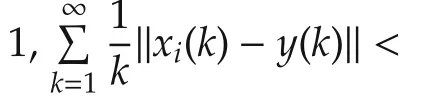
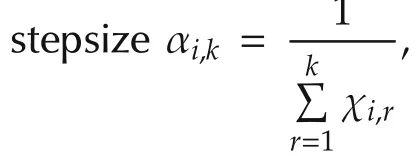
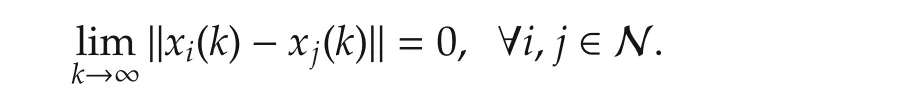
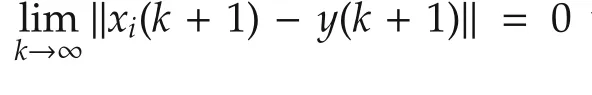
By Theorem 1,‖xi(k+1)-y(k+1)‖converges in mean.According to Fatou’s Lemma([29]),

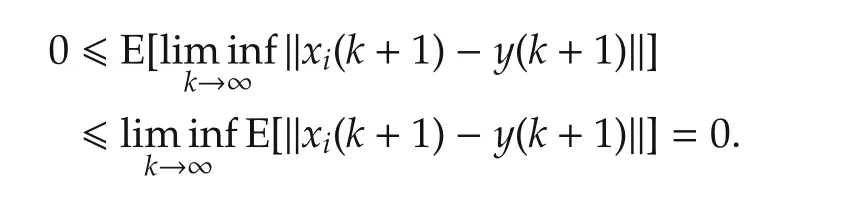
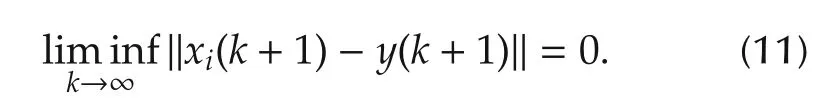
Then we only need to show that‖xi(k+1)-y(k+1)‖converges with probability 1.

For agenti∈Jk,we define

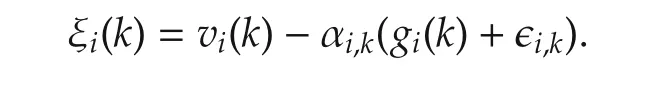
Sincexi(k+1)=PX[ξi(k)]for agenti∈Jk,by the nonexpansive property of projection we have

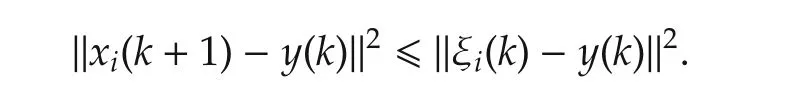
For agenti∈Jk,

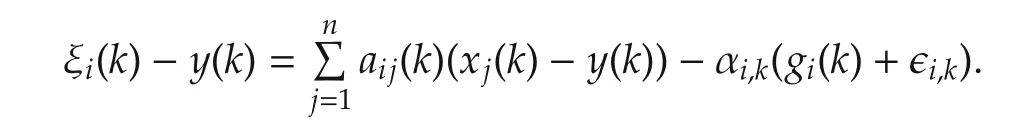
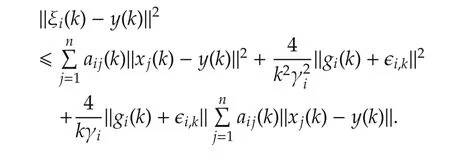
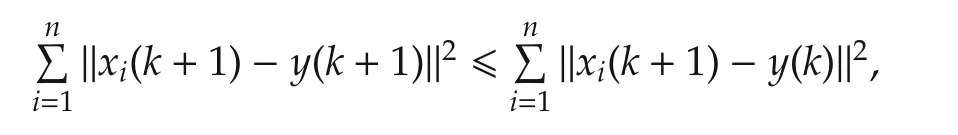
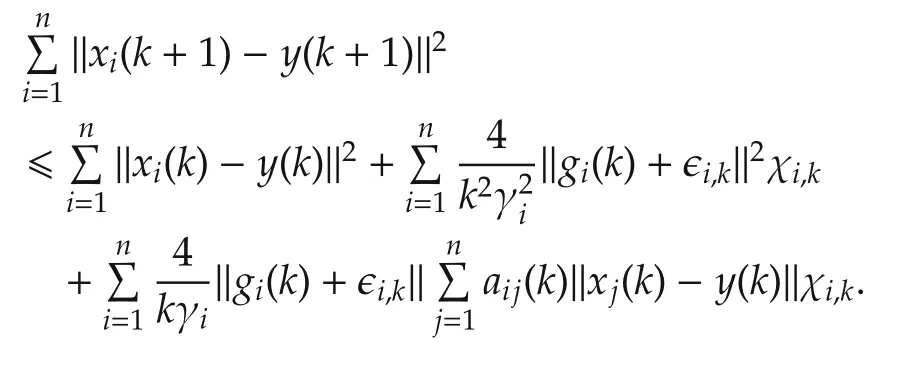
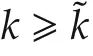
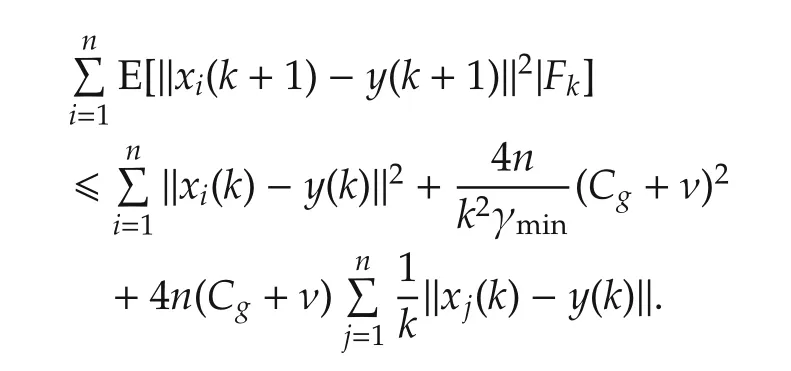
Thus,combined with(11),all the agents reach consensus with probability 1. □

3.2 Convergence result

Next result shows that all the agents reach the same optimal solution of(1)almost surely.

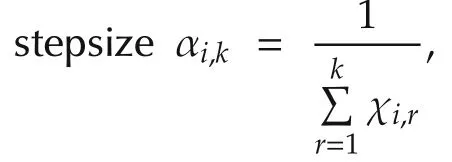
ProofLet x＊be any point in the optimal solution set X＊.Then for i∈ Jk,

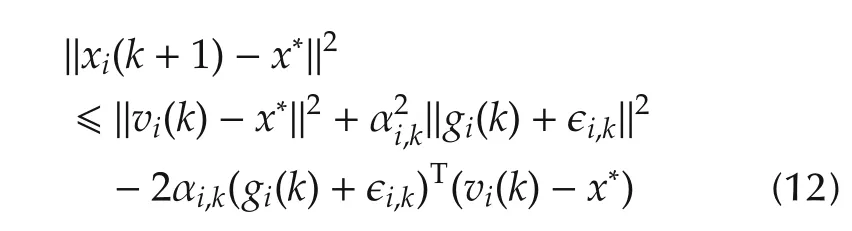
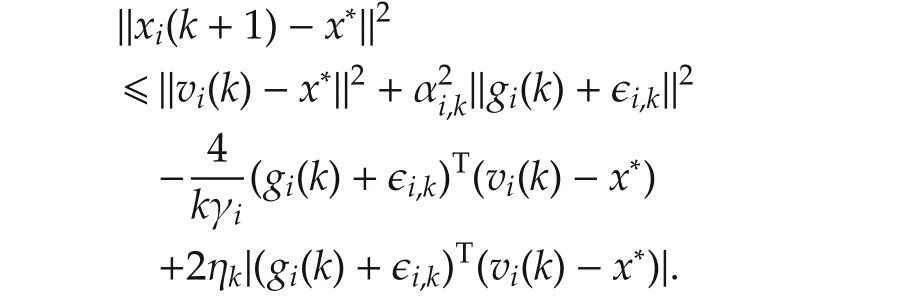
For 2ab ≤ a2+b2,we have 2ηk|(gi(k)+ϵi,k)T(vi(k)-x＊)|≤ηk‖vi(k)-x＊‖2+ ηk‖gi(k)+ ϵi,k‖2.Therefore,

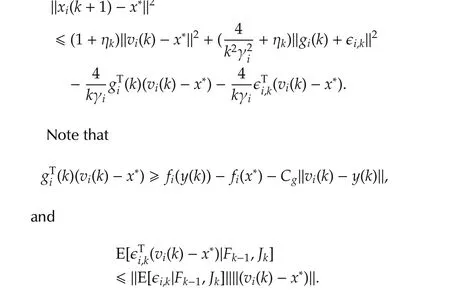
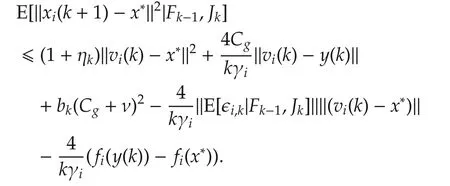
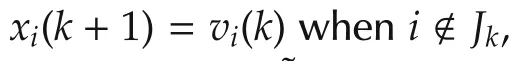
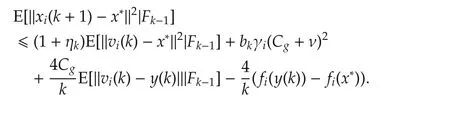
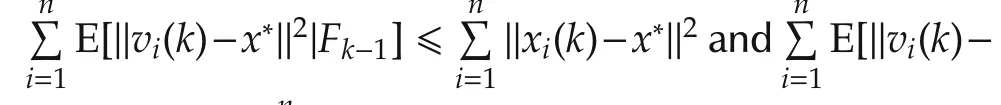
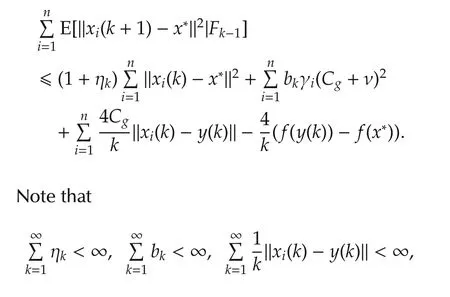
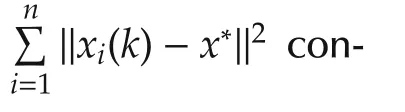
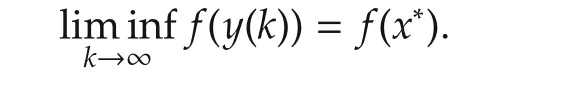
4 Errorbound analysis underf i xed stepsize

In some cases,a fixed stepsize policy may be adopted to facilitate the update of agents(referring to[1,2,9]).In fact,with the fixed stepsize,each agent can adapt with the changing environments while diminishing stepsize cannot.Because the agents cannotconverge to the exact optimal solution under fixed stepsize,which was proved in[11],we analyze the error bound in this section.

Suppose that all the agents use the same fixed stepsize αi,k= α in the distributed algorithm(2).Denote γmin=min{γ1,...,γn}and γmax={γ1,...,γn},which represent the minimal and the maximal update rate in the network.The following result gives the consensus error bounds analysis.

Lemma 6With Assumptions 1-3 and fixed stepsize αi,k= α,by the random sleep algorithm(2),we have

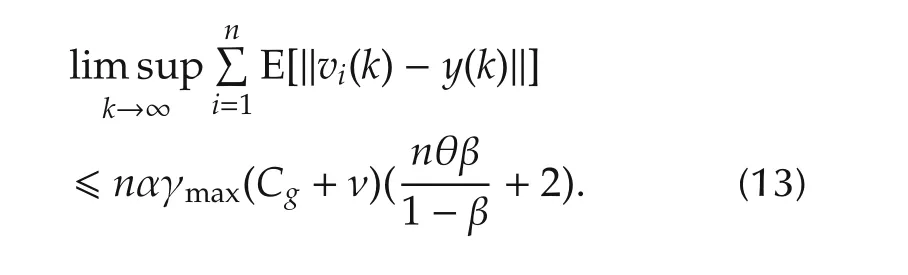
ProofIt is not hard to obtain

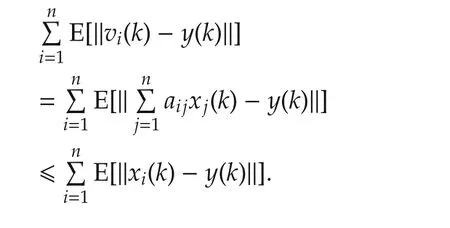
Using ζi(k)given in Theorem 1,and with fix stepsize,from equation(4),we have

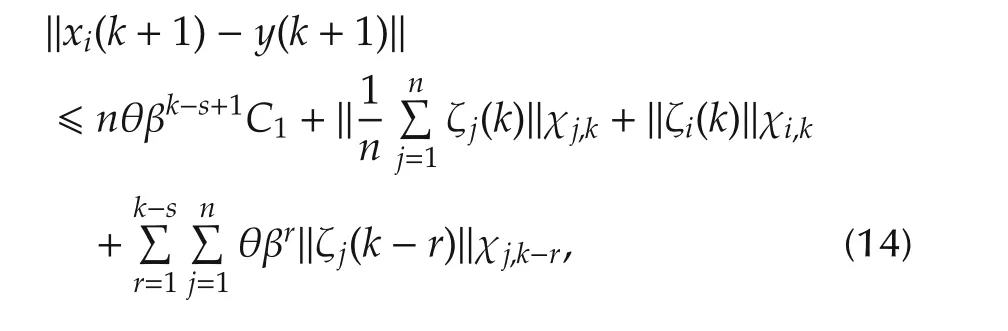
where the last step follows from Lemma 1 and Assumption 1.

With fixed stepsize αi,k= α,

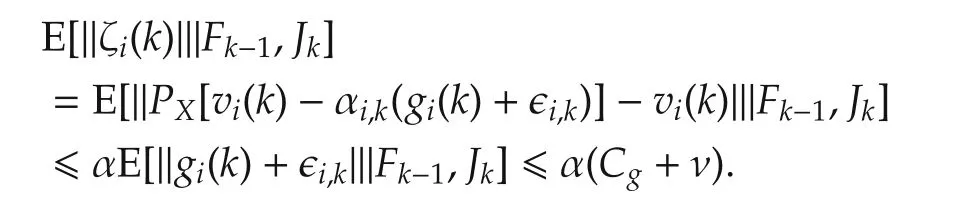
Therefore,taking the conditional expectation of(14)with respect toFs-1,we have

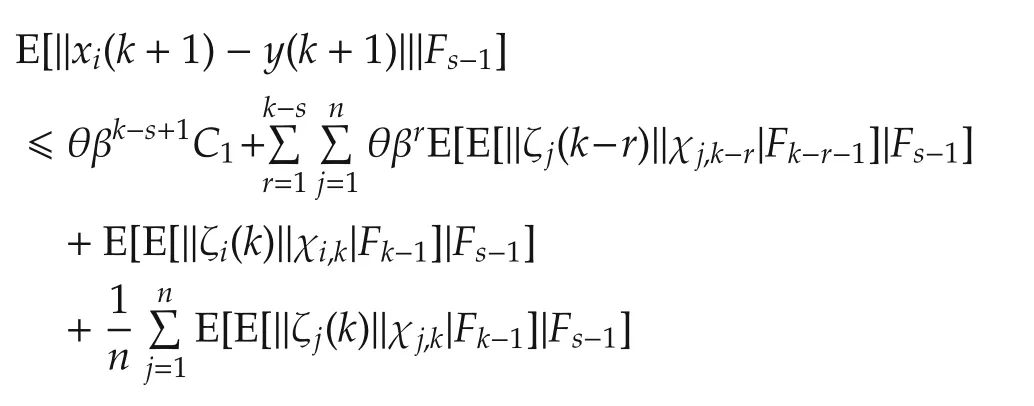
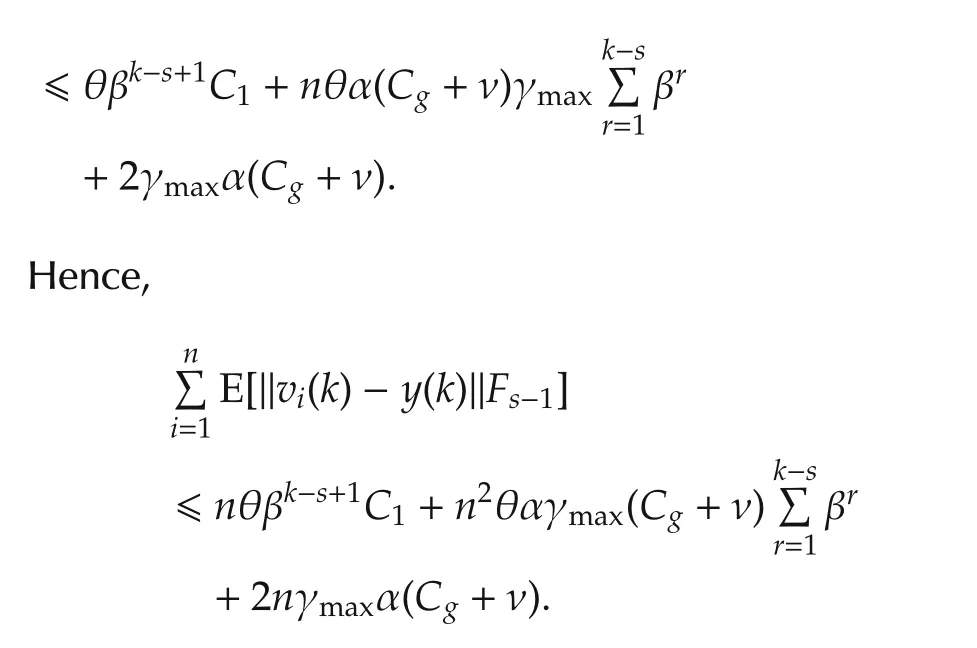
Taking full expectation and the limits yields(13). □

Remark 2Lemma 6 shows that smaller update rate γileads to smaller consensus error,which is consistent with the result in[23].

4.1 Strongly convex objective function

Here we analyze the distance between the agents’estimates and the optimal solution when the local objective functions are differentiable and σ-strongly convex,that is,

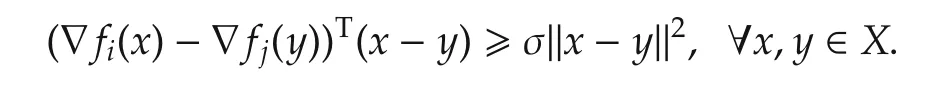
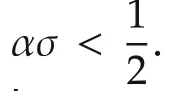
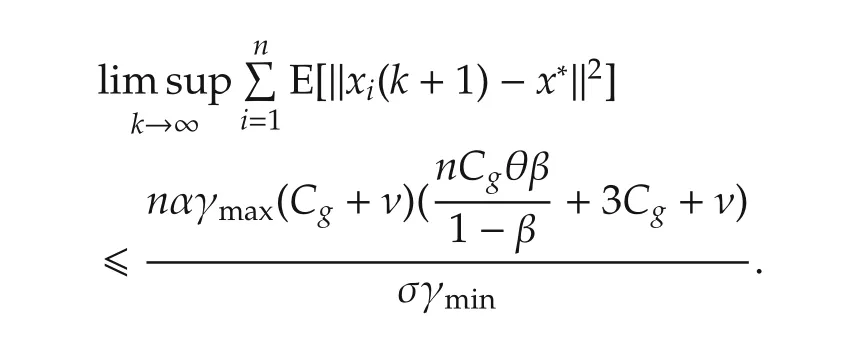
ProofWithout loss of generality,we still use the sub-gradient notation,though ∂f(x)={∇f(x)}here.With(2),for agenti∈Jk,

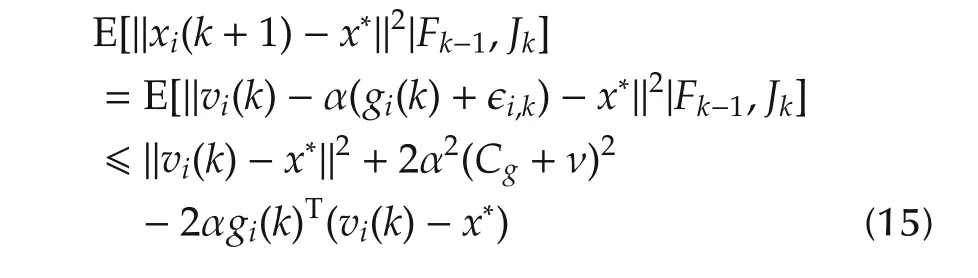
because (vi(k)-x＊)is measurable to {Fk-1,Jk},E[ϵi,k|Fk-1,Jk]=0,

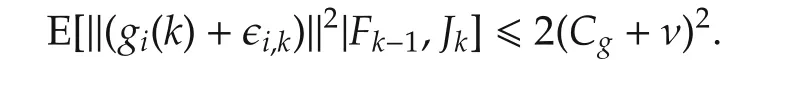
Moreover,because the local objective functions are σ-strongly convex,

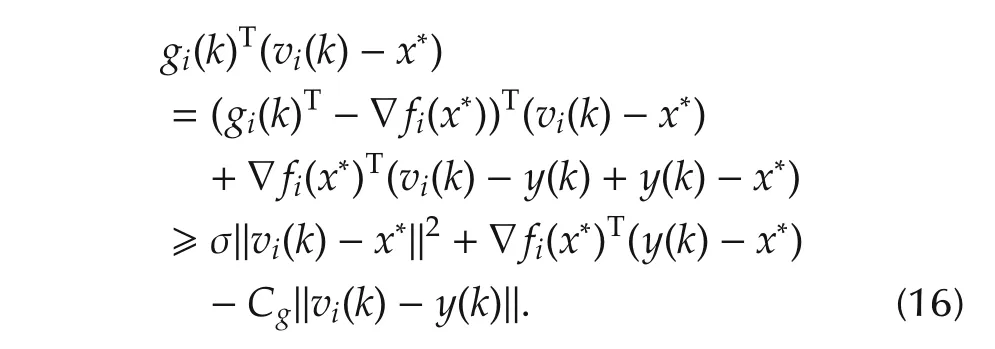
Hence,fori∈Jk,

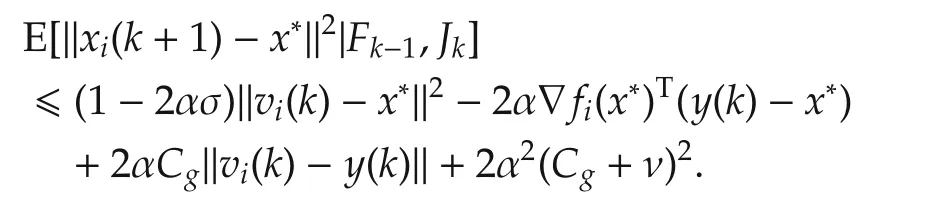
Hence,for all agents,

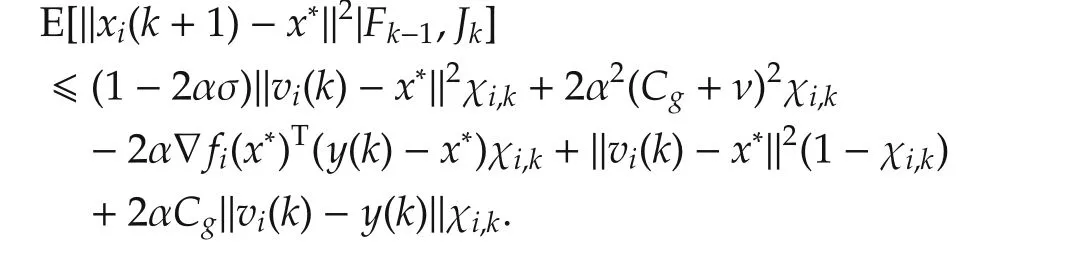
Take the expectation with respect toFk-1,

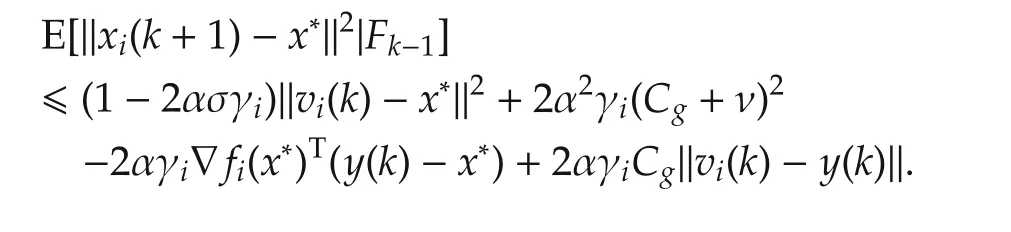
Summing up above equation fromi=1 tongives

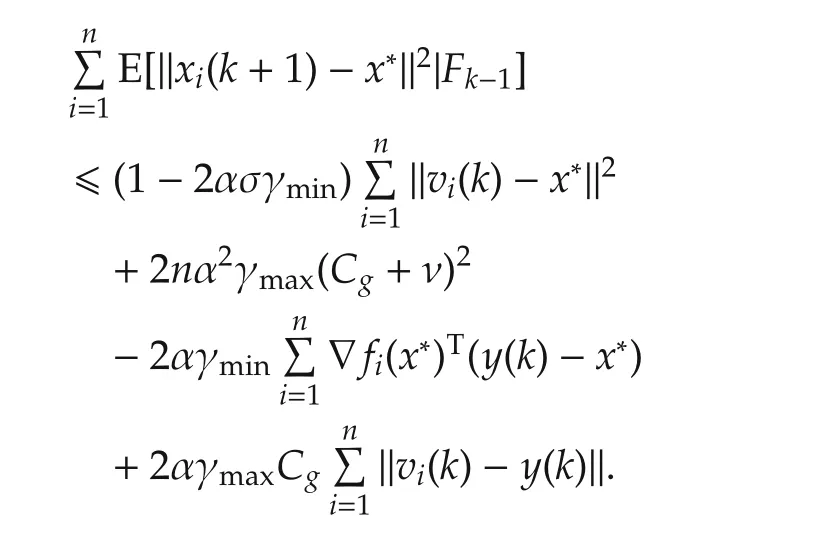
Therefore,

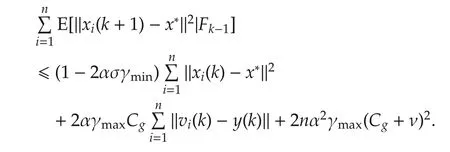
By Lemmas 2 and 6,we obtain

4.2 Nonsmooth convex objective functions

In this part,we apply the time averaging technique in[27]to study the gap between the function value at the estimate and the optimal value when the local objective functions are nonsmooth convex functions.

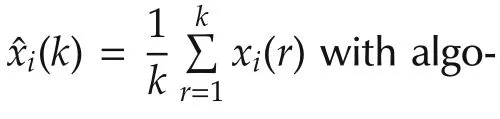
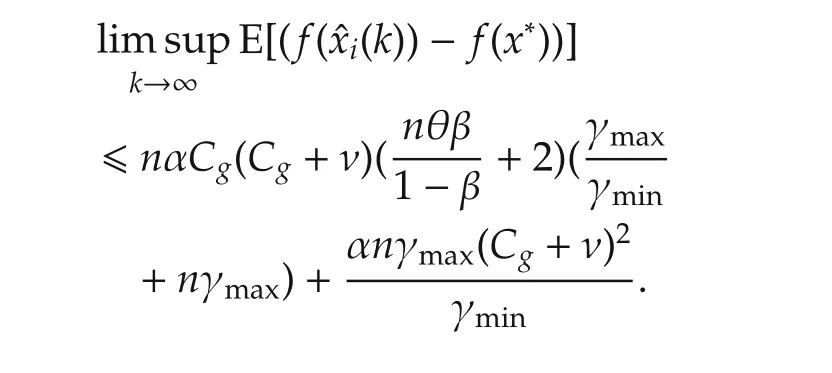
ProofFor agenti∈Jk,by the non-expansive of projection operation,(15)still holds.

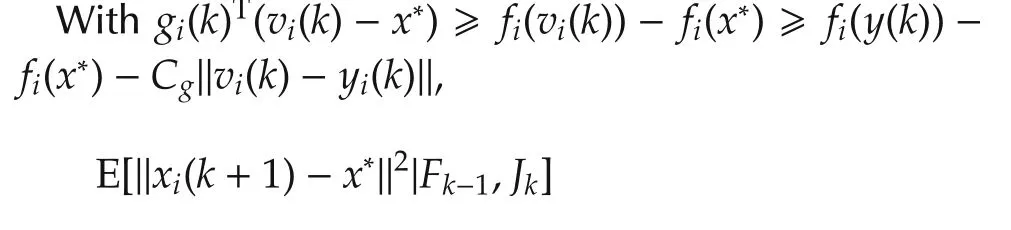
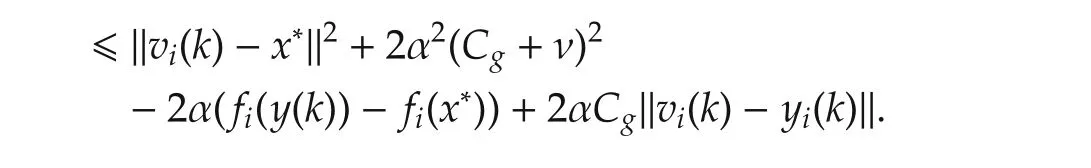
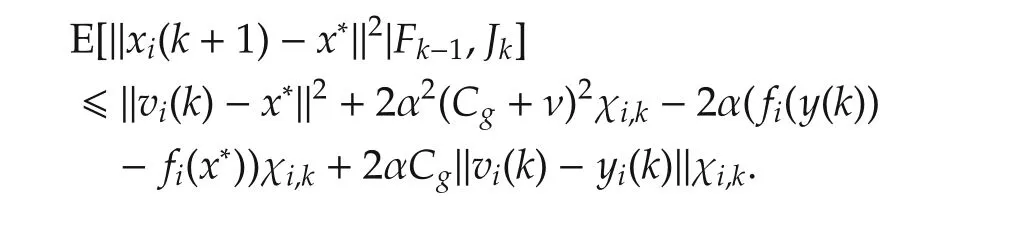
Hence,take an expectation with respect toFk-1,

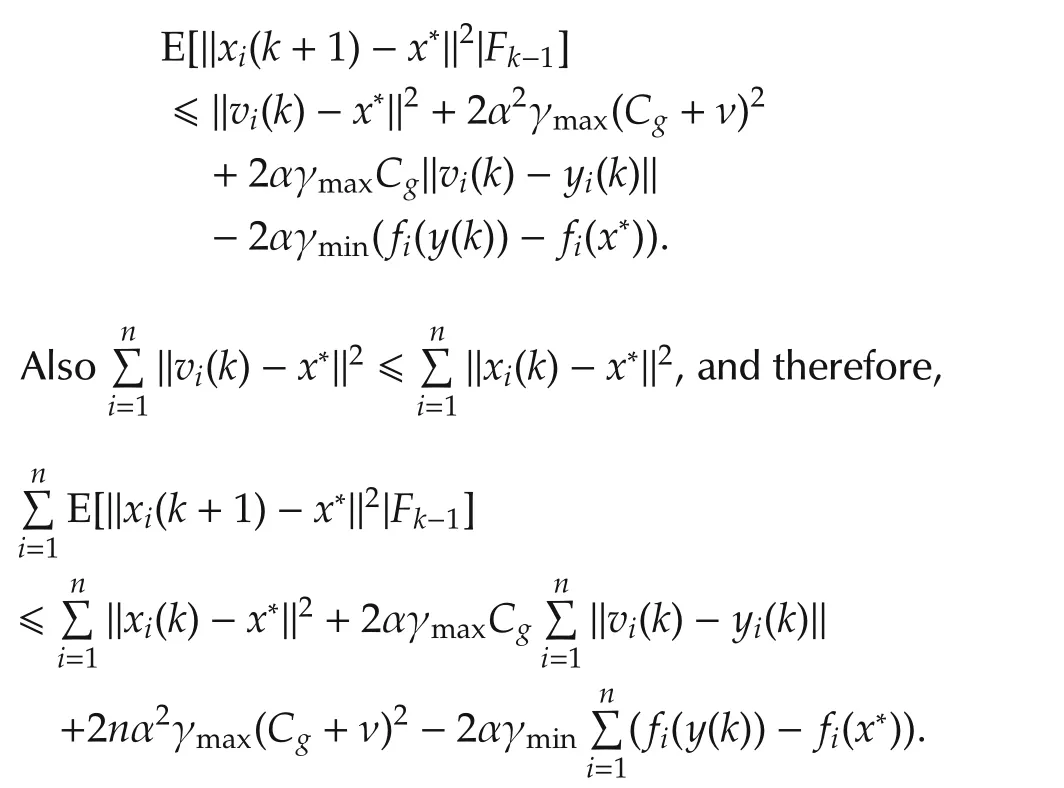
Denoting κ =2nγmax(Cg+ ν)2and taking full expectation,we have

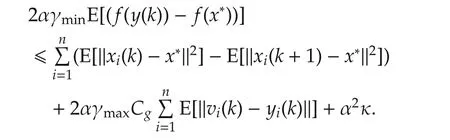
Summing up fromr=1 tor=kgives

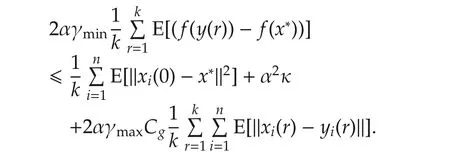
As a result,

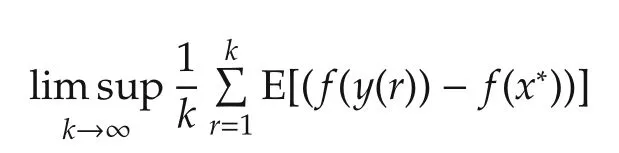
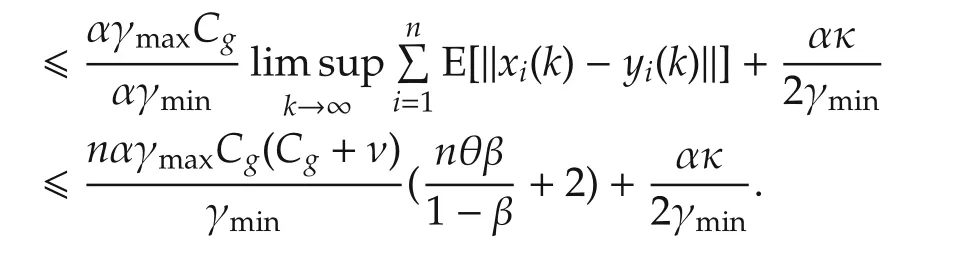
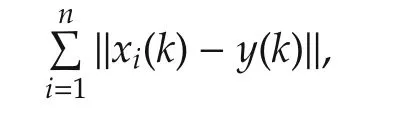
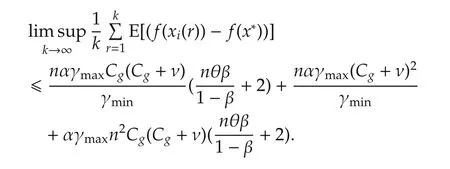
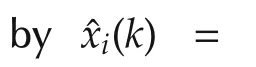
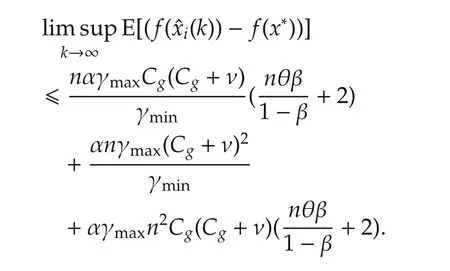
Then simple manipulations yield the conclusion. □

5 Numerical examples

In this section,two numerical examples are given to illustrate the algorithm performance.Example 1 shows the algorithm convergence with the randomized diminishing stepsize when the local objective functions are nonsmooth,while Example 2 illustratesthe performance for distributed quadratic optimization with the fixed stepsize.

Example 1Consider five agents solving the optimization problem(1)with x=(θ1,θ2)T∈ R2where

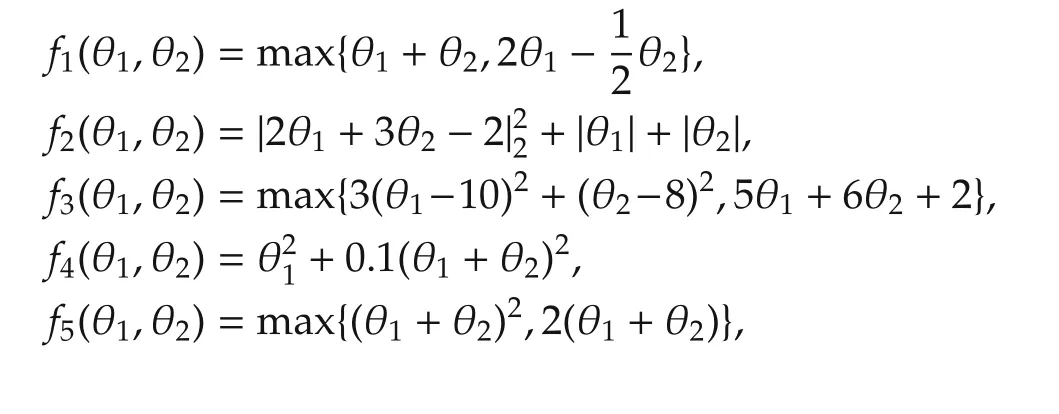
and the constraint set X ⊂ R2is X={x=(θ1,θ2)T∈R2:(θ1-1)2+θ22-1 ≤ 0,θ21+θ22-1 ≤ 0,θ2≥ 0}.The optimal solution is(0.978,0.206).

The five agents share information with the topologies G1,G2,G3,G4,switched periodically as shown in Fig.1.

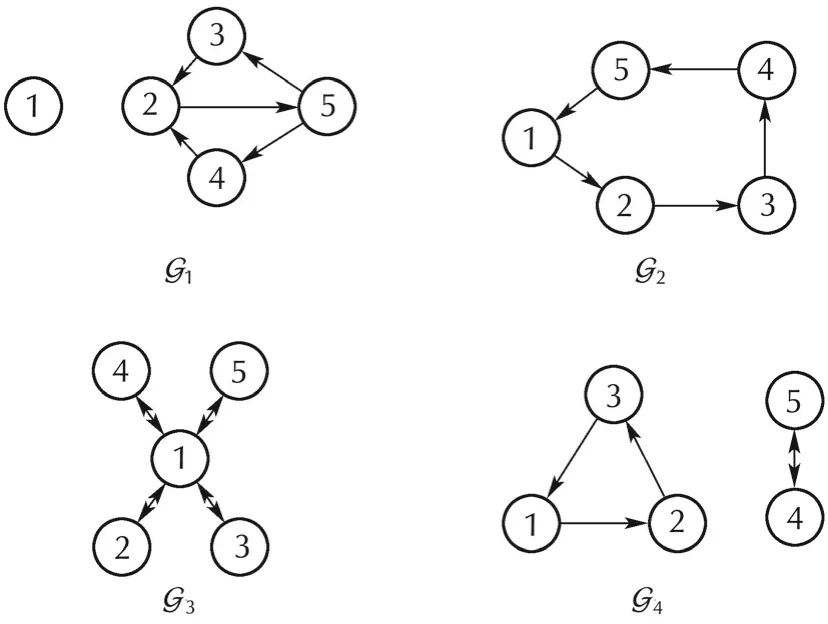
Fig.1 The communication graphs.

The corresponding mixing matrices Aiare given as

The agents are assumed with the same update rate γi= γ.The sub-gradient can be calculated corrupted with gaussian noise N(0,1)with zero mean and variance 1.

Let γ =0.5,then,the trajectories of estimates for θ1and θ2of the random sleep algorithm versus the standard algorithm(γ=1)are shown in Fig.2.

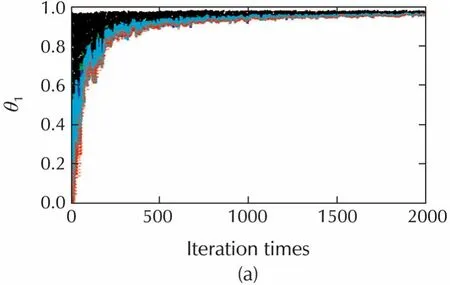
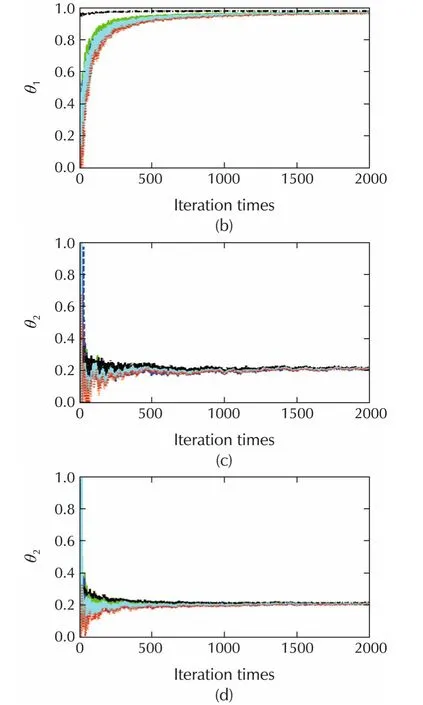
Fig.2 Trajectories of estimates for γ =0.5 and γ =1.The trajectories behave almost the same,but the random sleep algorithm(γ=0.5)has only half subgradients calculation times of the standard algorithm(γ=1)without sleeping.(a)The estimates of θ1,γ =0.5.(b)The estimates of θ1,γ =1.(c)The estimates of θ2,γ =0.5.(d)The estimates of θ2,γ =1.

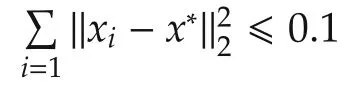
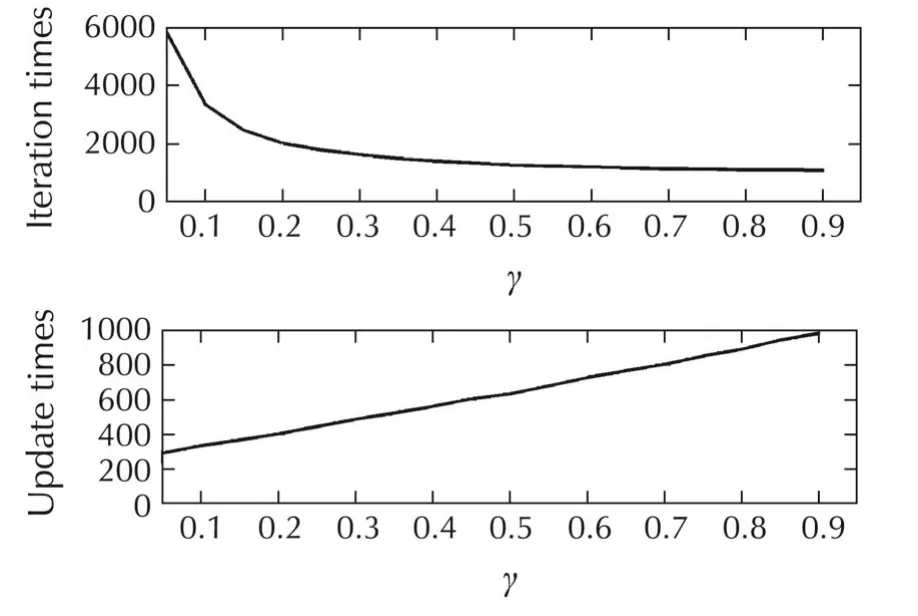
Fig.3 Iteration times and update times versus update rates γ:It shows that raising the update rate deceases the iteration times,meanwhile,increases the update times,to reach the same stopping criterion.Hence,the selection of update rate should be a trade off between iteration time requirement and computation burden.

Example 2 is given to illustrate the performance for differentiable strongly convex objective functions with fixed stepsize.

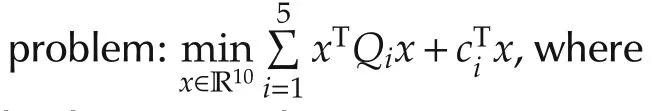
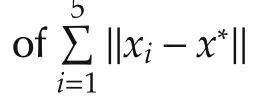
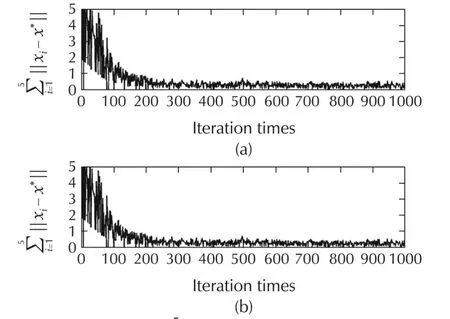
Fig.4 TrajectoriesThe trajectories behave almost the same,but(a)the random sleep algorithm(γ=0.5)has only half update times of(b)the standard algorithm(γ=1)without sleeping.

6 Conclusions

In this paper,we proposed a distributed sub-gradient algorithm with random sleep scheme for convex constrained optimization problems.Because stochastic(sub-)gradient noise was also taken into consideration,the algorithm generalized some existing results.We gave convergence analysis under both randomized diminishing stepsizes and fixed stepsizes,and also numerical simulations.

Acknowledgements

The authors would like to thank Dr.Youcheng Lou very much for his fruitful discussions.

[1]A.Nedic,A.Ozdaglar.Distributed subgradient methods for multi-agentoptimization.IEEE Transactions on Automatic Control,2009,54(1):48-61.

[2]A.H.Sayed,S.Tu,J.Chen,et al.Diffusion strategies for adaptation and learning over networks.IEEE Signal Processing Magazine,2013,30(3):155-171.

[3]G.Shi,K.H.Johansson,Y.Hong.Reaching an optimalconsensus:dynamical systems that compute intersections of convex sets.IEEE Transactions on Automatic Control,2013,58(3):610-622.[4]Y.Lou,G.Shi,K.H.Johansson,et al.An approximate projected consensus algorithm for computing intersection of convex sets.IEEE Transactions on Automatic Control,2014,59(7):1722-1736.

[5]P.Yi,Y.Zhang,Y.Hong.Potential game design for a class of distributed optimization problems.Journal of Control and Decision,2014,1(2):166-179.

[6]P.Yi,Y.Hong.Quantized subgradient algorithm and data-rate analysis fordistributed optimization.IEEE Transactions on Control of Network Systems,2014,1(4):380-392.

[7]P.Yi,Y.Hong,F.Liu.Distributed gradient algorithm for constrained optimization with application to load sharing in power systems.Systems&Control Letters,2015,83:45-52.

[8]S.Ram,A.Nedic,V.V.Venugopal.Distributed stochastic subgradient projection algorithms for convex optimization.Journal of Optimization Theory and Applications,2010,147(3):516-545.

[9]A.Nedic.Asynchronous broadcast-based convex optimization over a network.IEEE Transactions on Automatic Control,2011,56(6):1337-1351.

[10]I.Lobel,A.Ozdaglar.Distributed subgradient methods for convex optimization over random networks.IEEE Transactions on Automatic Control,2011,56(6):1291-1306.

[11]K.Yuan,Q.Ling,W.Yin.On the convergence of decentralized gradient descent.arXiv,2013:http://arxiv.org/abs/1310.7063.

[12]J.C.Duchi,A.Agarwal,M.J.Wainwright.Dual averaging for distributed optimization:convergence analysis and network scaling.IEEE Transactions on Automatic Control,2012,57(3):592-606.

[13]D.Yuan,S.Xu,H.Zhao.Distributed primal-dual subgradient method for multiagent optimization via consensus algorithms.IEEE Transactions on Systems Man and Cybernetics:Part BCybernetics,2011,41(6):1715-1724.

[14]W.Shi,Q.Ling,G.Wu,et al.EXTRA:An exact first-order algorithm fordecentralized consensus optimization.SIAM Journal on Optimization,2015,25(2):944-966.

[15]J.Wang,Q.Liu.A second-order multi-agent network for bound-constrained distributed optimization.IEEE Transactions on Automatic Control,2015:DOI 10.1109/TAC.2015.241692.

[16]V.Cevher,S.Becker,M.Schmidt.Convex optimization for big data:Scalable,randomized,and parallel algorithms for big data analytics.IEEE Signal Processing Magazine,2014,31(5):32-43.

[17]H.Lakshmanan,D.P.Farias.Decentralized resource allocation in dynamic networks of agents.SIAM Journal on Optimization,2008,19(2):911-940.

[18]D.Yuan,D.W.C.Ho.Randomized gradient-free method for multiagent optimization over time-varying networks.IEEE Transactions on Neural Networks and Learning Systems,2015,26(6):1342-1347.

[19]K.Kvaternik,L.Pavel.Analysis of Decentralized Extremum-Seeking Schemes.Toronto:Systems Control Group,University of Toronto,2012.

[20]N.Atanasov,J.L.Ny,G.J.Pappas.Distributed algorithms for stochastic source seeking with mobile robot networks.ASME Journal on Dynamic Systems,Measurement,and Control,2015,137(3):DOI 10.1115/1.4027892.

[21]G.Shi,K.H.Johansson.Randomized optimal consensus of multiagent systems.Automatica,2012,48(12):3018-3030.

[22]Y.Lou,G.Shi,K.H.Johansson,et al.Convergence of random sleep algorithms for optimal consensus.Systems&Control Letters,2013,62(12):1196-1202.

[23]D.Jakovetic,J.Xavier,J.M.F.Moura.Fast distributed gradient methods.IEEE Transactions on Automatic Control,2014,59(5):1131-1146.

[24]D.Jakovetic,D.Bajovic,N.Krejic,et al.Distributed gradient methods with variable number of working nodes.arXiv,2015:http://arxiv.org/abs/1504.04049.

[25]J.Liu,X.Jiang,S.Horiguchi,et al.Analysis of random sleep scheme for wireless sensor networks.International Journal of Sensor Networks,2010,7(1):71-84.

[26]H.Fan,M.Liu.Network coverage using low duty-cycled sensors:random&coordinated sleep algorithms.Proceedings of the 3rd International Symposium on Information Processing in Sensor Networks,New York:ACM,2004:433-442.

[27]B.T.Polyak.Introduction to Optimization.New York:Optimization Software Inc.,1987.

[28]T.Li,L.Xie.Distributed consensus over digital networks with limited bandwidth and time-varying topologies.Automatica,2011,47(9):2006-2015.

[29]R.B.Ash.Real Analysis and Probability.New York:Academic Press,1972.

Peng YIis a Ph.D.candidate at the Academy of Mathematics and Systems Science,Chinese Academy of Sciences.He received his B.Sc.degree of Automation from University of Science and Technology of China in 2011.His research interest covers multi-agents system,distributed optimization,hybrid system and smart grid.E-mail:yipeng@amss.ac.cn.

†Corresponding author.

E-mail:yghong@iss.ac.cn.

This work was supported by the Beijing Natural Science Foundation(No.4152057),the National Natural Science Foundation of China(No.61333001)and the Program 973(No.2014CB845301/2/3).

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg

the B.Sc.and M.Sc.degrees from Peking University,Beijing,China,and the Ph.D.degree from the Chinese Academy of Sciences(CAS),Beijing.He is currently a professor in Academy of Mathematics and Systems Science,CAS,and serves as the Director of Key Lab of Systems and Control,CAS and the Director of the Information Technology Division,National Center for Mathematics and Interdisciplinary Sciences,CAS.His research interests include nonlinear dynamics and control,multi-agent systems,distributed optimization,social networks,and software reliability.E-mail:yghong@iss.ac.cn.