Linear quadratic regulation for discrete-time systems with state delays and multiplicative noise

Lin LI,Huanshui ZHANG

School of Control Science and Engineering,Shandong University,Jinan Shandong 250061,China Received 21 March 2015;revised 25 September 2015;accepted 25 September 2015

Linear quadratic regulation for discrete-time systems with state delays and multiplicative noise

Lin LI,Huanshui ZHANG†

School of Control Science and Engineering,Shandong University,Jinan Shandong 250061,China Received 21 March 2015;revised 25 September 2015;accepted 25 September 2015

In this paper,the linear quadratic regulation problem for discrete-time systems with state delays and multiplicative noise is considered.The necessary and sufficient condition for the problem admitting a unique solution is given.Under this condition,the optimal feedback control and the optimal cost are presented via a set of coupled difference equations.Our approach is based on the maximum principle.The key technique is to establish relations between the costate and the state.

Optimal control,time-delay system,multiplicative noise

DOI 10.1007/s11768-015-5036-z

1 Introduction

Delay exists widely in areas of economics,physics,biology,chemistry and mechanics[1].This makes the study oftime-delay systems,which can modelprocesses with delay,greatly significantin both theory and application.The research in this field includes stability and stabilization[2-4],optimal control[5,6],H∞control[7,8],etc.As an important part of the optimal control theory,the linear quadratic regulation(LQR)problem for timedelay systems has been extensively studied.For example,[9]focuses on continuous-time linear systems with state delay.A sufficient condition for a feedback control to be optimal is established via a set of differential equations.For other literature on this subject,see[10-12]and references therein.

Stochastic uncertainty is another important subject in the control theory.In practical situation,there exist various kinds of noises and disturbances.As a result,stochastic systems can characterize the real process more accurately.Stochastic systems can be naturally classified as continuous-time ones and discretetime ones.Continuous-time stochastic systems are usu-ally described by Itˆo-type differential equations governed by Brownian motion.Systems which correspond to the discretization of Itˆo-type differential equations are those with multiplicative noises.For works concerning stochastic control,readers are referred to[13,14]in continuous time and[15,16]in discrete time.

Many control problems have been studied for systems with both time delay and stochastic uncertainty in the literature.These problems include stability and stabilization[17,18],estimation[19],and optimal control[20-22].Reference[20]considers discrete-time stochastic systems with a single inputdelay.By using the stochastic maximum principle,it presents a complete solution to the finite-horizon LQR problem.It establishes a necessary and sufficient condition for the existence of a unique optimal controller and gives an explicit optimal controller via a Riccati-ZXL difference equation.Reference[21]is concerned with the finite-horizon LQR problem for continuous-time stochastic systems with state and inputdelays.The optimalfeedback controlleris given by a new type of Riccati equations whose solvability is not easy to obtain.To the best of our knowledge,previous works on the LQR problem for state-delay systems in both deterministic setting and stochastic setting usually assume that the weighting matrix of the control in the quadratic cost function is strictly positive definite and only give sufficient conditions for the existence of an optimal control;see[9],[12]and[21].Motivated by this,we are devoted to using the method in[20]to solve the LQR problem for stochastic systems with multiple state delays and aim to derive a necessary and sufficient condition for the existence of an explicit optimal control under the condition that the weighting matrix of the control is positive semi-definite.Readers may think that a possible way to settle this problem is to change it into a delay-free one by incorporating the history state into an augmented state.However,the resultant solution is a high-dimensional Riccati equation,which causes computational burden as pointed out by[7].

The contributions of the paper lie in that a necessary and sufficient condition for the LQR problem admitting a unique solution is given and under this condition,the optimal feedback control and the optimal cost are presented in terms of coupled difference equations.The main technique is to solve the maximum principle,which can be viewed as delayed forward(the state equation)and delayed backward(the costate equation)stochastic difference equations.The optimal costate is expressed as a linear function of a finite length of state and the corresponding coefficient matrices satisfy the above-mentioned coupled difference equations.

The rest of the paper is organized as follows.In Section 2,the stochastic LQR problem for state-delay systems is formulated.Section 3 presents the solution to the problem.Section 4 provides the proof of the main results.Section 5 uses numerical examples to illustrate the results.Section 6 makes a conclusion.Some details of proof are given in Appendix.

NotationRnstands for the usual n-dimensional Euclidean space;Rn×mis the space of real matrices with order n×m;The superscript′means the matrix transpose;I denotes the unit matrix;A symmetric matrix M＞0(reps.≥0)means that it is strictly positive definite(reps.positive semi-definite);For a random variable ξ and a σ-algebra F,E(ξ)and E(ξ|F)represents the mathematical expectation of ξ and the conditional expectation of ξ with regards to F,respectively; δi,jis the usual Kronecker function,i.e.,δi,i=1 and δi,j=0 if i≠j.

2 Problem statement

Consider the following discrete-time system with state delays and multiplicative noise:

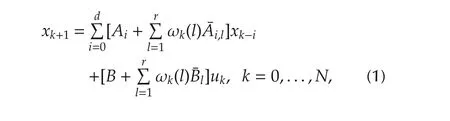
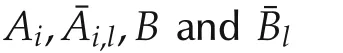
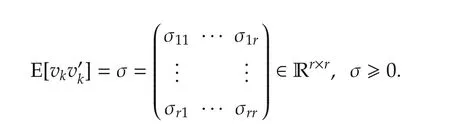
Let Fkbe the natural filtration generated by vk,i.e.,Fkis the σ-algebra generated by{v0,...,vk}.

Consider the cost function

whereQ≥0,R≥0 andW≥0.Define the admissible control set as

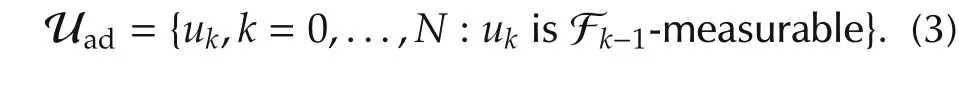
The problem to be addressed is stated as follows.

Problem1Finduk∈Uadto minimize the costfunction(2)subject to system(1).

Remark 1(1)is a discrete-time system which admits two features:one is the time delay and another is the white noisevk.Its possible application can be found in networked control systems(NCSs)with transmission delay as pointed out by[17].Moreover,a special case of system(1)whenvkis an independent Bernoulli process is often used to describe packet dropout in NCSs;see[23]and[24].

3 Main results

3.1 A special case:scalar noise

In this section,we will focus on a special case of system(1)withr=1:

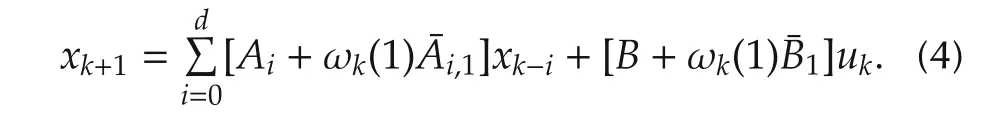
Problem2Finduk∈Uadto minimize the costfunction(2)subject to system(4).

Motivated by the approach proposed in[25],the maximum principle for Problem 2 is derived as

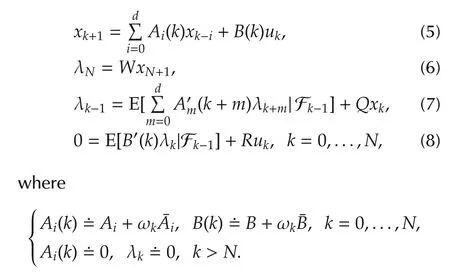
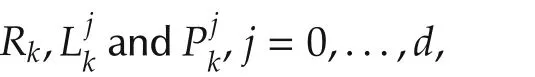
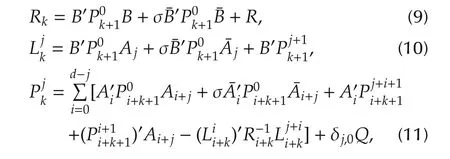
where the terminal value is given by

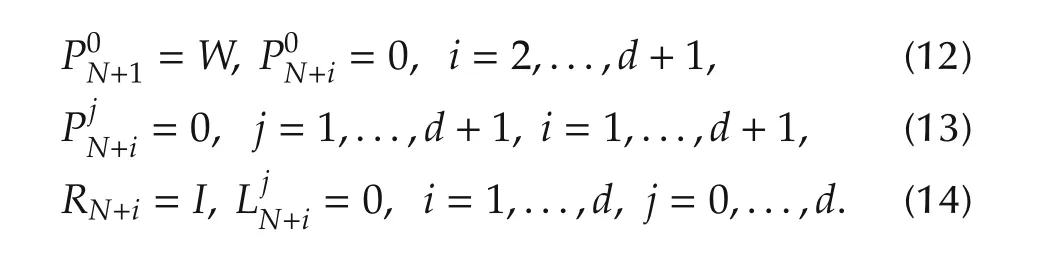
Theorem 1Problem 2 has a unique solution if and only if

fork=N,...,0.In this case,the unique optimal controlukand the optimal value of(2)are respectively

In addition,the following relation between the optimal costate and the state holds:

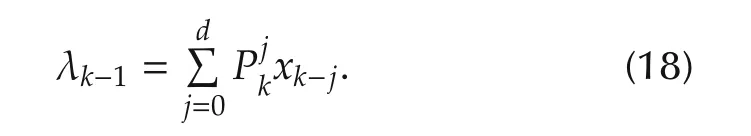
The proof of Theorem 1 will be provided in the next section.

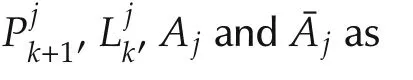
for the convenience of simplicity.

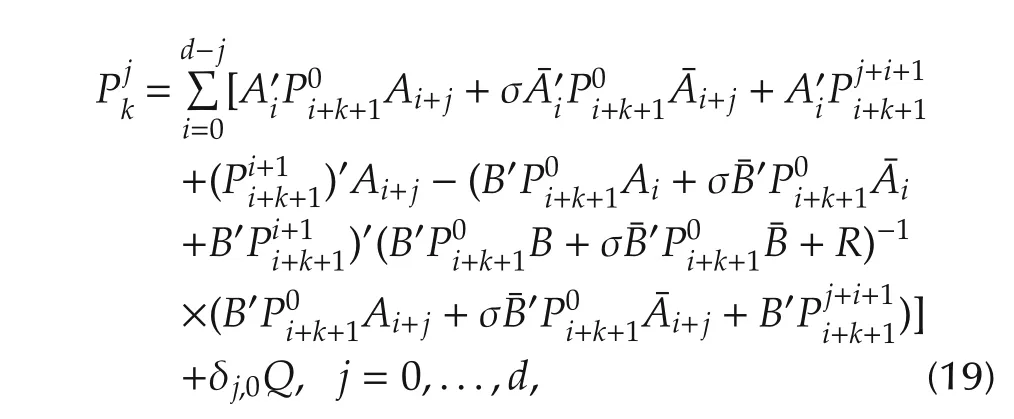
with terminal value(12)and(13).The role of equation(19)in our problem is the same as that of the generalized difference Riccati equation in the standard stochastic LQR problem[15].

Remark 4This remark is to make clear the differences of this paper from our previous one[20].

▪First,problems considered in these two papers are completely different.Reference[20]studies the LQR problem for the following system with a single input delay:

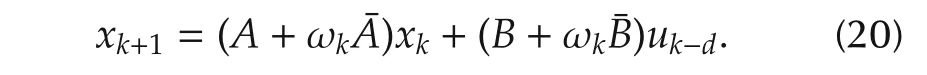
While this paper focuses on system(1)which is with multiple state delays.Obviously,(20)and(1)are essentially different.

▪Second,the maximum principle in[20]is given by

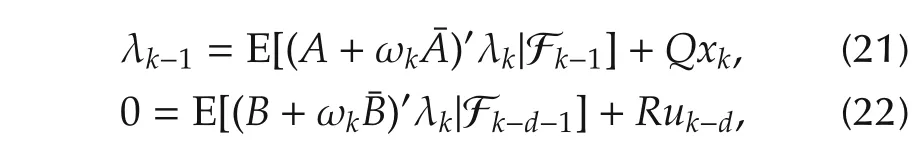
where the equilibrium equation is with a single inputdelay.In this paper,the adjoint equation(7)is a backward difference equation with multiple delays.Equations(4)-(8)are more difficult to solve than(20)-(22)(see Section 4).

▪Third,the results are different.In[20],the optimal controller is shown to be a predictor form as

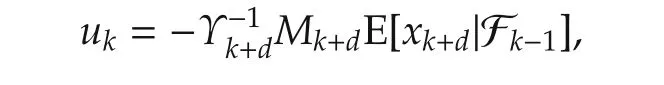
where E[xk+d|Fk-1]is the conditional expectation ofxk+dwith respect to Fk-1and can be expressed as

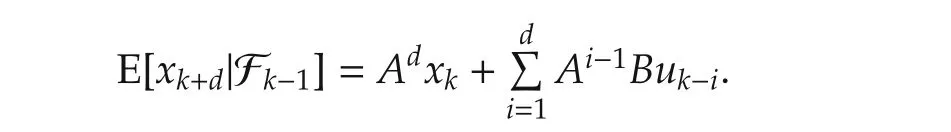
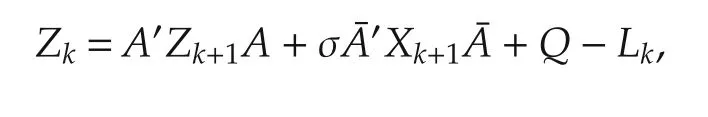
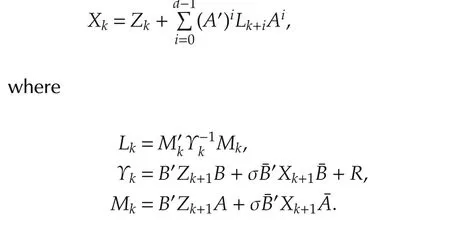
While in this paper,the optimal controller has the form as(16)which involves a finite length of history states.In addition,the gains are determined by the coupled difference equations(19).

Remark 5This paper concentrates on the finitehorizon LQR problem.By showing the convergence of the solution to equations(19)whenNtends to+∞,we can derive the corresponding results in infinite-horizon case.On the other hand,combination of this paper with[22],which is concerned with the LQR problem for systems with multiple input delays,will yield results for systems with both multiple state delays and multiple input delays.

3.2 Solution to Problem 1

Next,we shall extend the results in the previous section to system(1).The increase of the dimension of the white noise does not cause any essential changes.A counterpart of Theorem 1 will be presented without proof.

Theorem 2Problem 1 admits a unique optimal control iff

fork=N,...,0,whereRkis given by the following coupled difference equations:

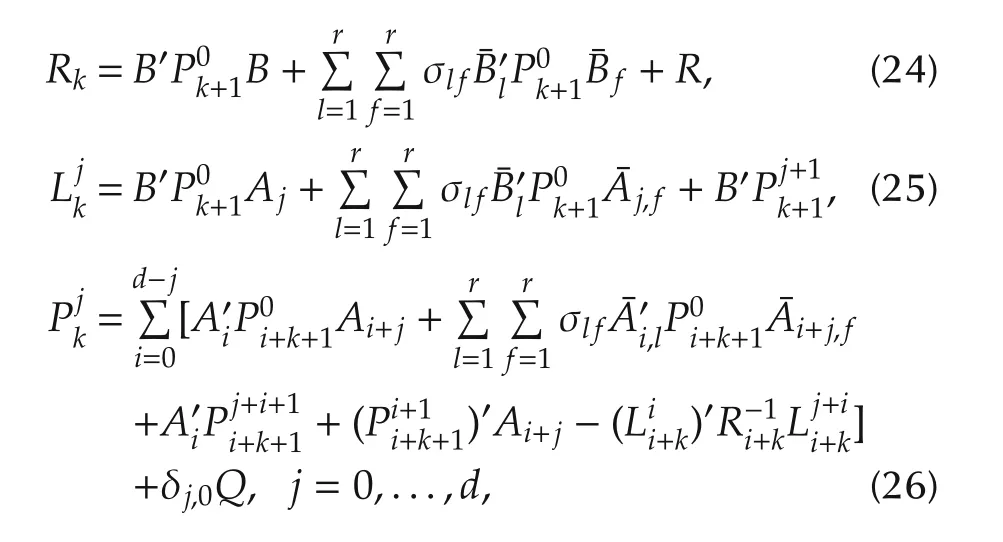
with terminal value as(12)-(14).Under this condition,the unique optimal control and the optimal cost are as

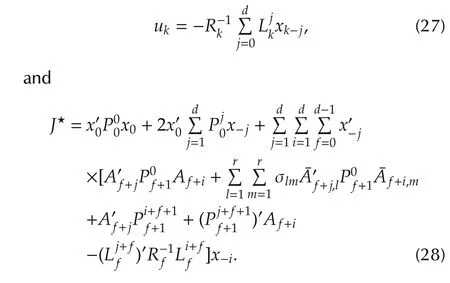
4 Derivation of the main results

4.1 Necessity of Theorem 1

Suppose that Problem 2 admits a unique solution.We will show that the matrixRkdefined by(9)-(14)is positive definite,the unique optimal control is as(16),and the optimal costate λk-1can be expressed like(18).

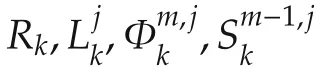
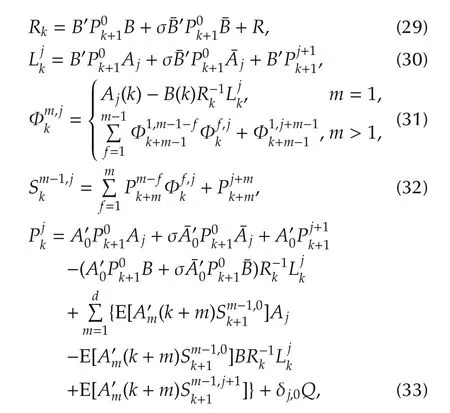
with terminal value given by

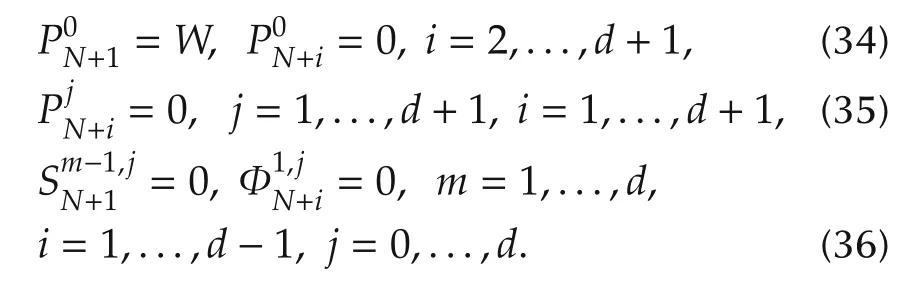
Suppose that Problem 2 has a unique optimal control,thenRk,which has been defined above,satisfies

fork=N,...,0.The optimal control possesses the form of

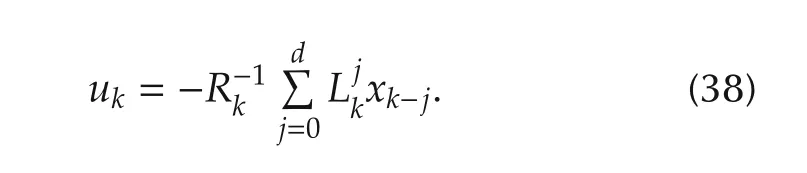
When the control is optimal,the following relations hold

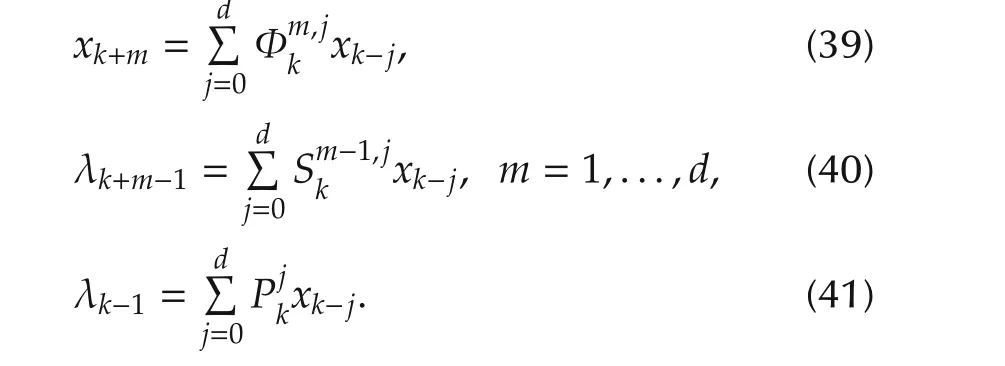
ProofSee Appendix.

Lemma 2Fork=0,...,N,there holds

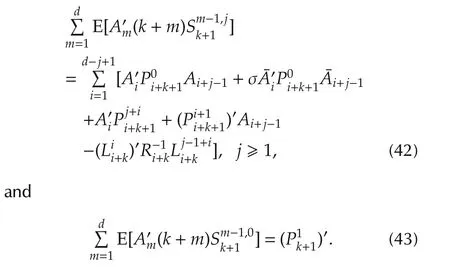
ProofSee Appendix.

Finally,it can be shown that(33)can be rewritten as(11)with the help of(42)and(43).This process is completely similar to the derivation of(a16),so details are not provided here.

4.2 Suff i ciency of Theorem 1

ProofSupposeRk＞0 fork=N,...,0 whereRkis determined by(9)-(14),then it will be proven that the unique solution to Problem 2 is(16)and the optimal value of(2)is(17).To this end,define

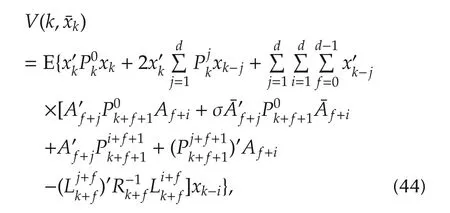
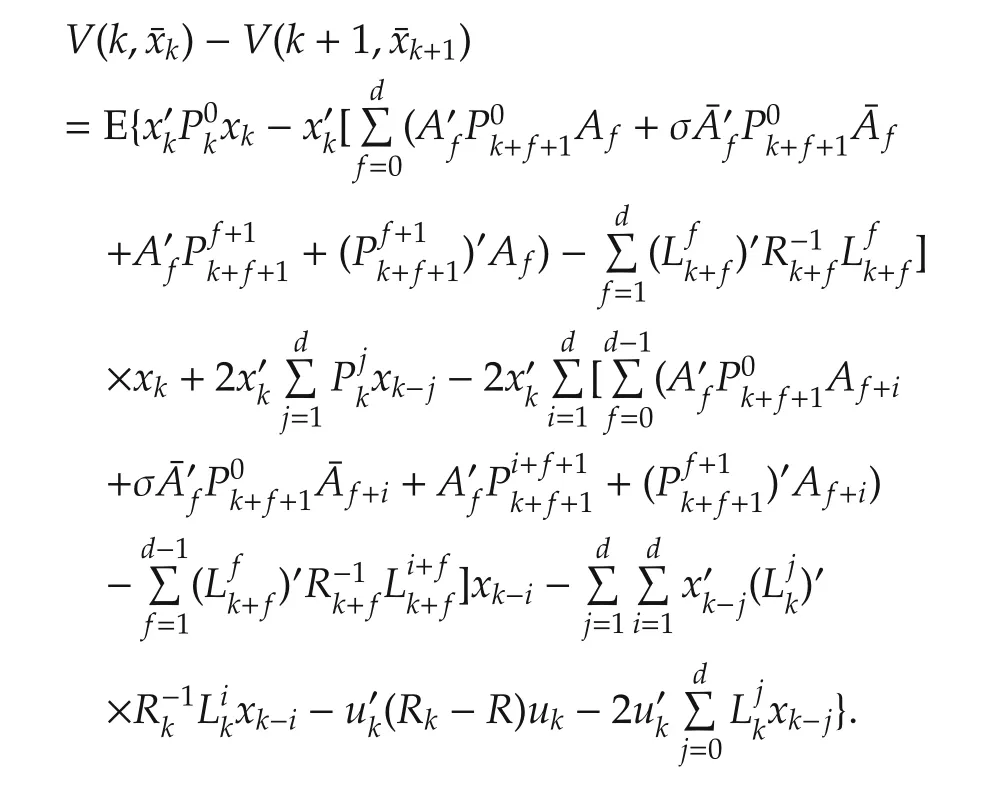
In view of the invertibility of Rk,we can complete the square in the above equation as

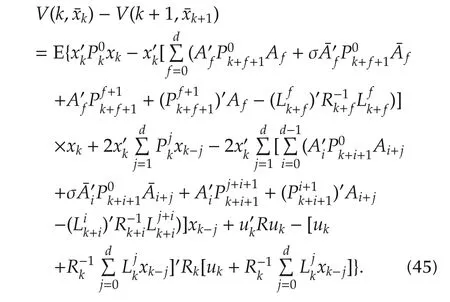
By making use of(11),(45)is further rewritten as

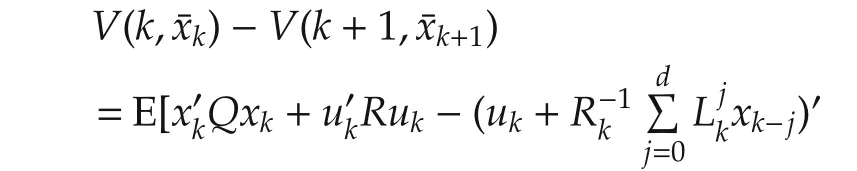
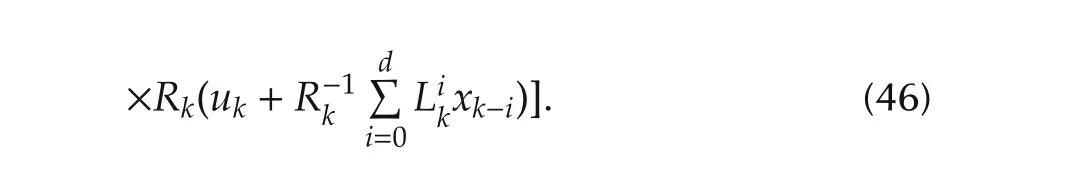
On both sides of(46),take sums from k=0 to k=N.It leads to

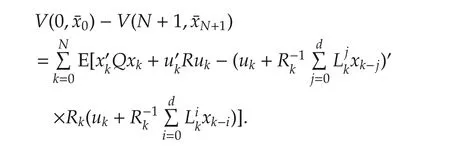
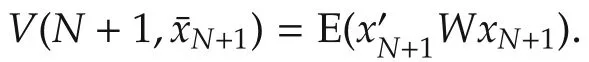
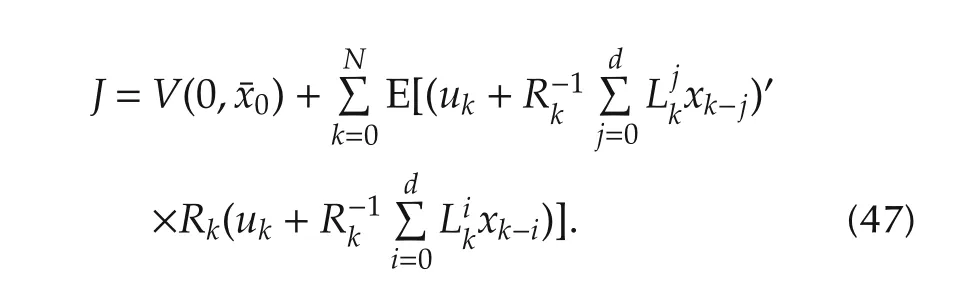
5 Numerical examples

Example 1Consider system(4)where both xkand ukare scalar and

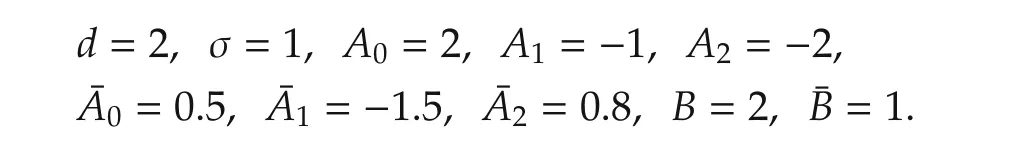
In the cost function(2),we set

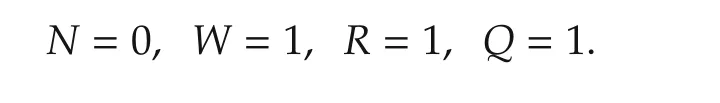
By direct computation,we can obtain the solution to the backwards recursion(9)-(14)as

Note that R0＞0.Thus from Theorem 1,it follows that the unique optimal control of Problem 2 is given by

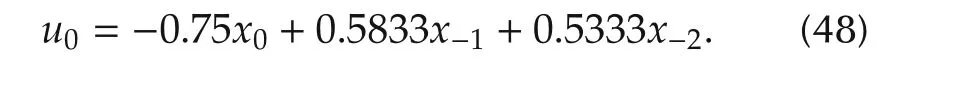
To show the effectiveness of our results,we will compare the values of(2)under the controller(48)and the following one

Denote the value of(2)with(48)by J★and that with(49)by J.Five cases with different initial values are considered below.

1)x0=2,x-1=0,x-2=0,J★=7.5000,J=16.3807,

2)x0=2.2,x-1=-3,x-2=1,J★=25.6533,J=25.7420,

3)x0=1,x-1=-2.8,x-2=1,J★=18.5550,J=20.0056,

4)x0=0,x-1=-5,x-2=2,J★=63.2750,J=83.8100,

5)x0=3,x-1=1,x-2=-4,J★=156.4333,J=311.6145.

In all cases,controller(48)generates a smaller value for(2)than(49).This coincides with Theorem 1.

Example 2Consider system(4)where xk∈R2,uk∈ R2,d=1,σ =1,and

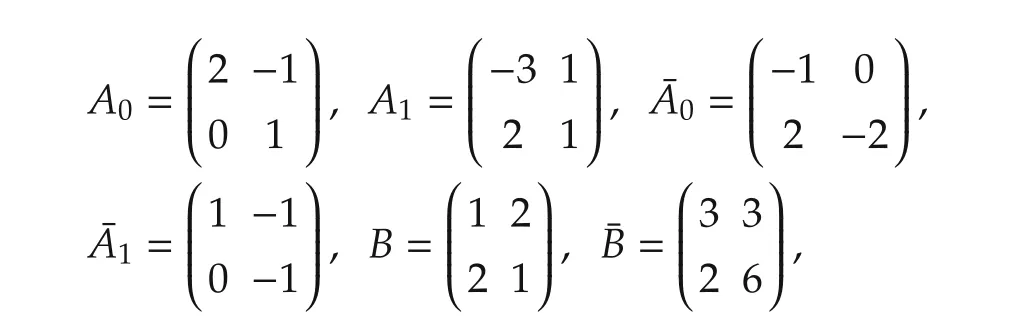
and the cost function(2)where

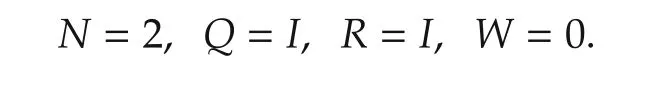
The solution to(9)-(14)is derived as

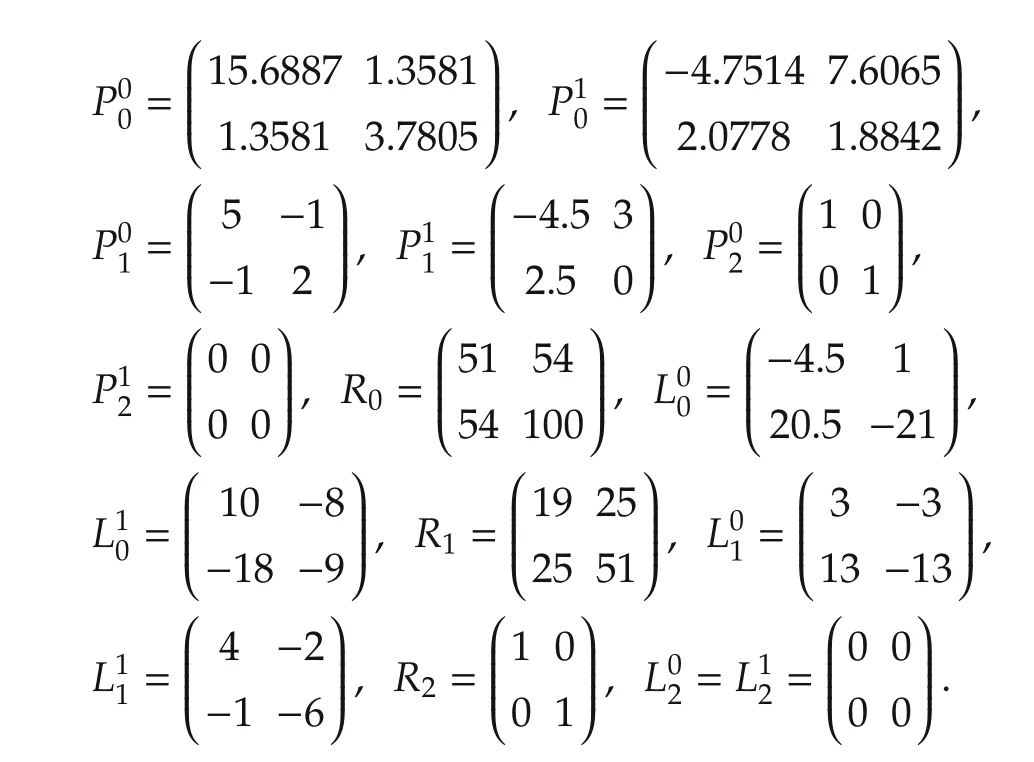
It can be easily verified that R0,R1and R3are all positive definite.Hence,according to Theorem 1,the unique optimal controller is

When the initial value is chosen to be

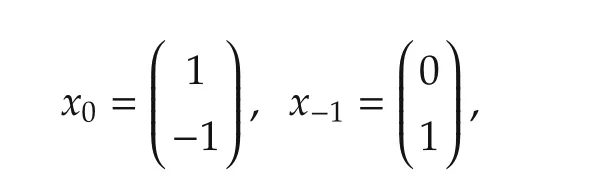
the optimal cost is

If the controller is changed into

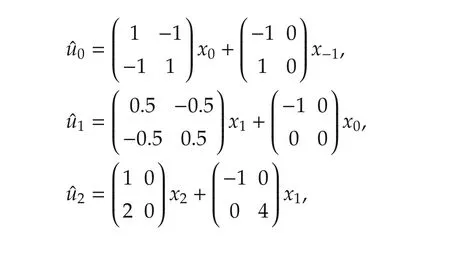
the associated value of the cost function is

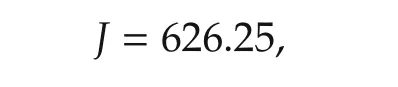
which is larger than(50).

6 Conclusions

This paper solves the LQR problem for stochastic systems with state delays in discrete-time case.The coupled difference equations developed here play the same role in our problem as the generalized difference Riccati equation does in the standard stochastic LQR problem.The stabilization problem for this class of systems is worth considering in the future.

[1]V.B.Kolmanovskii,A.Myshkis.Introduction to the Theory and Applications of Functional Differential Equations.Dordrecht:Kluwer Academy,1999.

[2]A.W.Olbrot.A sufficiently large time delay in feedback loop must destroy exponential stability of any decay rate.IEEE Transactions on Automatic Control,1984,AC-29(4):367-368.

[3]K. Gu. Discretization schemes for Lyapunov-Krasovskii functionals in time delay systems.Kybernetica,2001,37(4):479-504.

[4]G.Meng,K.Ma.Global output feedback stabilization of uppertriangularnonlineartime-delay systems.JournalofControlTheory and Applications,2012,10(4):533-538.

[5]M.Maleki,I.Hashim.Adaptive pseudospectral methods for solving constrained linear and nonlinear time-delay optimal control problems.Journal of the Franklin Institute,2014,351(2):811-839.

[6]N.Haddadi,Y.Ordokhani,M.Razzaghi.Optimal control of delay systems by using a hybrid functions approximation.Journal of Optimization Theory and Applications,2012,153(2):338-356.

[7]G.Tadmor,L.Mirkin.H∞control and estimation with preview-Part II:fixed-size ARE solutions in discrete time.IEEE Transactions on Automatic Control,2005,50(1):29-40.

[8]H.H.Choi,M.J.Chung.Memoryless H∞controller design for linear systems with delayed state and control.Automatica,1995,31(6):917-919.

[9]D.H.Eller,J.K.Aggarwal,H.T.Banks.Optimal control of linear time-delay systems.IEEE Transactions on Automatic Control,1969,AC-16(6):678-687.

[10]M.C.Delfour.The linear-quadratic optimal control problem with delaysin state and controlvariables:a state space approach.SIAM Journal on Control and Optimization,1986,24(5):835-883.

[11]R.B.Vinter,R.H.Kwong.The infinite time quadratic control problem for linear systems with state and control delays:an evolution equation approach.SIAM Journal on Control and Optimization,1981,19(1):139-153.

[12]W.B.Arthur.Control of linear processes with distributed lags using dynamic programming from first principles.Journal of Optimization Theory and Applications,1977,23(3):429-443.

[13]S.Peng.A general stochastic maximum principle for optimal control problems.SIAM Journal on Control and Optimization,1990,28(4):966-979.

[14]J.Yong,X.Zhou.Stochastic Controls:Hamiltonian Systems and HJB Equations.New York:Springer,1999.

[15]M.A.Rami,X.Chen,X.Zhou.Discrete-time indefinite LQ controlwith state and controldependentnoises.JournalofGlobal Optimization,2002,23(3/4):245-265.

[16]E.Gershon,U.Shaked,I.Yaesh.H∞control and filtering of discrete-time stochastic systems with multiplicative noise.Automatica,2001,37(3):409-417.

[17]H.Gao,J.Lam,Z.Wang.Discrete bilinear stochastic systems with time-varying delay:stability analysis and control synthesis.Chaos,Solitons&Fractals,2007,34(2):394-404.

[18]L.Liu,Z.Han,X.Cai,et al.Robust stabilization of stochastic differential inclusion systems with time delay.Journal of Control Theory and Applications,2012,10(1):77-81.

[19]H.Bao,J.Cao.Delay-distribution-dependent state estimation for discrete-time stochastic neural networks with random delay.Neural Networks,2011,24(1):19-28.

[20]H.Zhang,L.Li,J.Xu,et al.Linear quadratic regulation and stabilization of discrete-time systems with delay and multiplicative noise.IEEE Transactions on Automatic Control,2015,60(10):2599-2613.

[21]L.Chen,Z.Wu,Z.Yu.Delayed stochastic linear-quadratic control problem and related applications.Journal of Applied Mathematics,2012:DOI 10.1155/2012/835319.

[22]L.Li,H.Zhang.Stochastic linear quadratic regulation for discretetime systems with single input and multiple delays.Proceedings of the 32nd Chinese Control Conference,Xi’an:IEEE,2013:2299-2304.

[23]O.C.Imer,S.Y¨uksel,T.Ba¸sar.Optimal control of LTI systems over unreliable communication links.Automatica,2006,42(9):1429-1439.

[24]L.Schenato,B.Sinopoli,M.Franceschetti,et al.Foundations of control and estimation over lossy networks.Procedings of the IEEE,2007,95(1):163-187.

[25]H.Zhang,H.Wang,L.Li.Adapted and casual maximum principle and analytical solution to optimal control for stochastic multiplicative-noise systems with multiple inputdelays.Proceddings of the 51st IEEE Conference on Decision and Control,Hawaii:IEEE,2012:2122-2127.

Appendix

Proof of Lemma 1Suppose that Problem 2 has a unique solution.(37)-(41)will be shown inductively on k=N,...,0.For simplicity,denote the cost function starting from time k,k=0,...,N,by

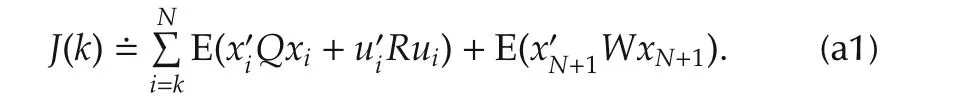
The verification of the case of k=N is simple and similar to the discussion given below.Thus it will be omitted.Inductively,suppose(37)-(41)hold for k≥n+1.We shall show that they are true for k=n.First,Rn＞0 is to be verified.To this end,set n to be the initial time and let the initial value be

Take unto be any Fn-1-measurable random variable and un+1,...,uNto be optimal.Now the optimal value of J(n+1)will be calculated.For k=n+1,...,N+1,denote

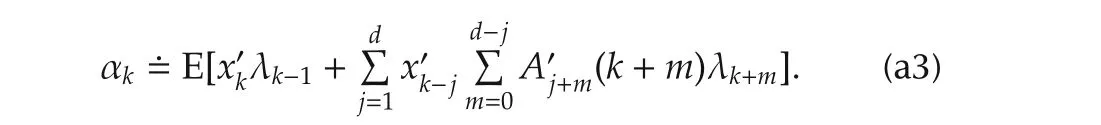
By(7),(5)and(8),it can be derived

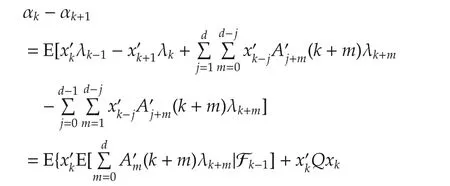
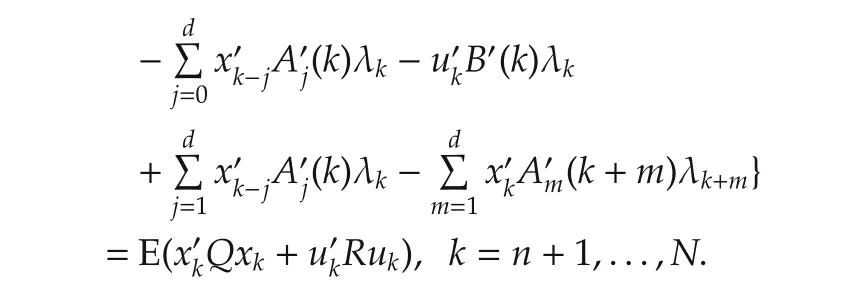
Summing from k=n+1 to k=N on the two sides of the above equation yields

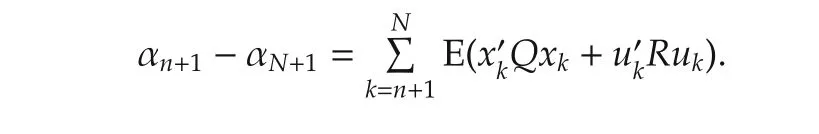
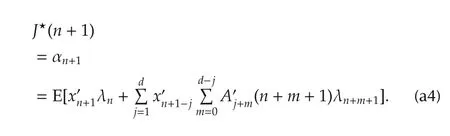
(41)is assumed to be true for k=n+1,i.e.,λnis as

By applying(a4),(a5),(a2)and(5),it leads to

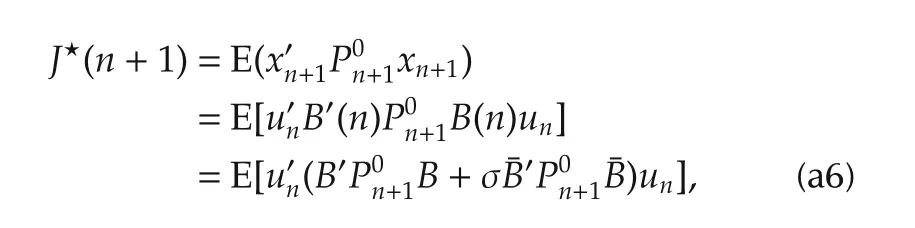
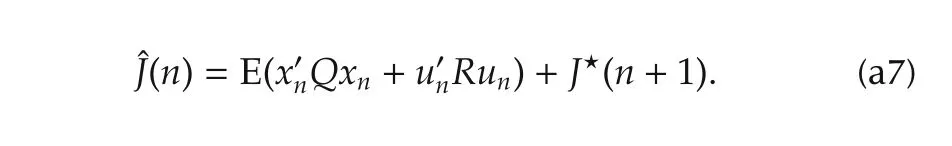
Furthermore,the weighting matrix of uninˆJ(n)must be positive definite.By substituting(a6)into(a7),it can be easily obtained that the weighting matrix is just Rn.Hence,Rn＞0 has been shown.

Second,the optimal unis to be solved.Substitution of(a5)and(5)into(8)produces

Combined with Rn＞0,it is readily seen that the optimal unis given by

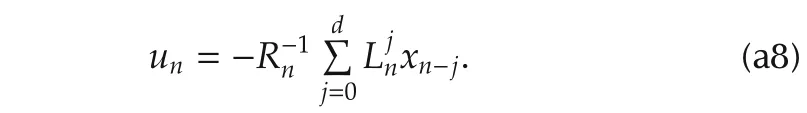
Third,let us verify(39)for k=n,i.e.,the following relation

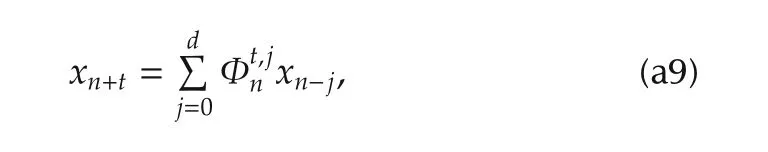
holds for t=1,...,d.The analysis will be made inductively on t.By substituting(a8)into(5),xn+1becomes

which is the case of t=1.Inductively,suppose(a9)is true for t=1,...,s.By applying(39)with k=n+s and m=1,one gets

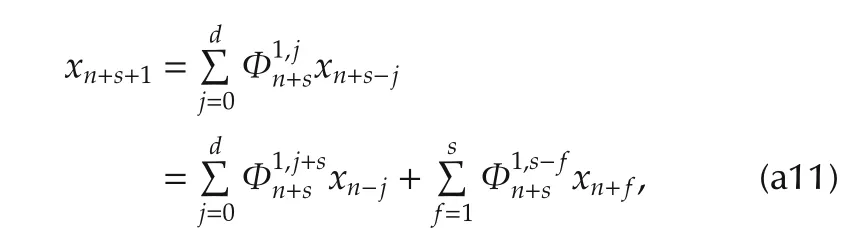
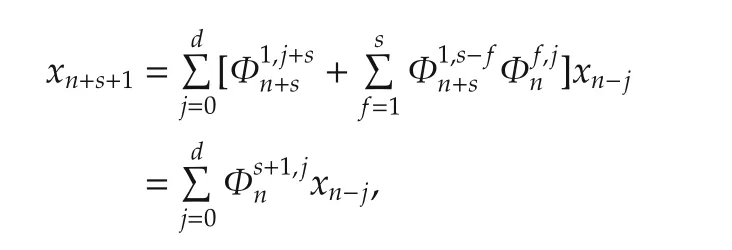
which is(a9)for t=s+1.Hence,(a9)has been shown inductively.

Next,(40)is to be proven for k=n and m=1,...,d.According to the inductive hypothesis,(41)is true for k=n+m,i.e.,

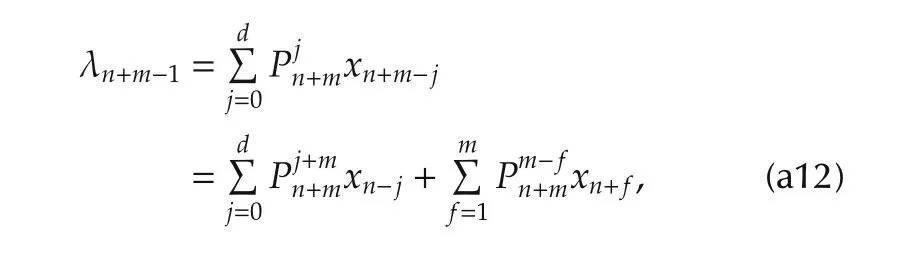
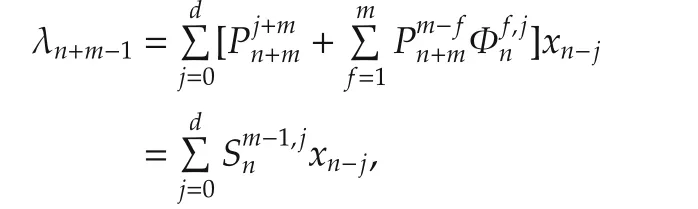
which is indeed(40)with k=n.

Finally,let us show(41)fork=n.In(40)and(41),settingk=n+1 produces

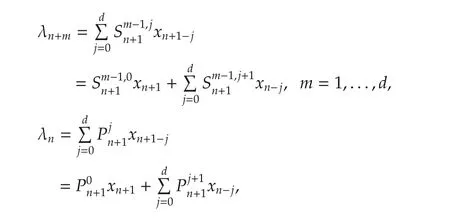
Substitution of(a13)and(a14)into(7)leads to

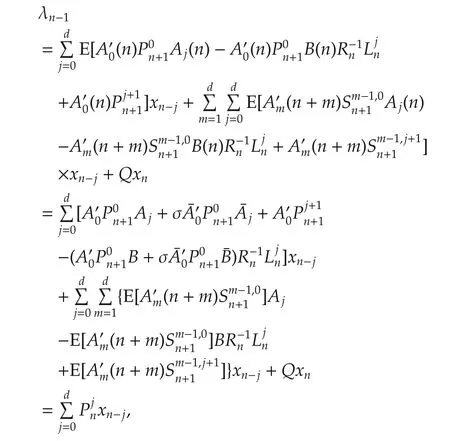
which is(41)fork=n.Until now,the proof of this Lemma is completed. □

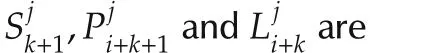
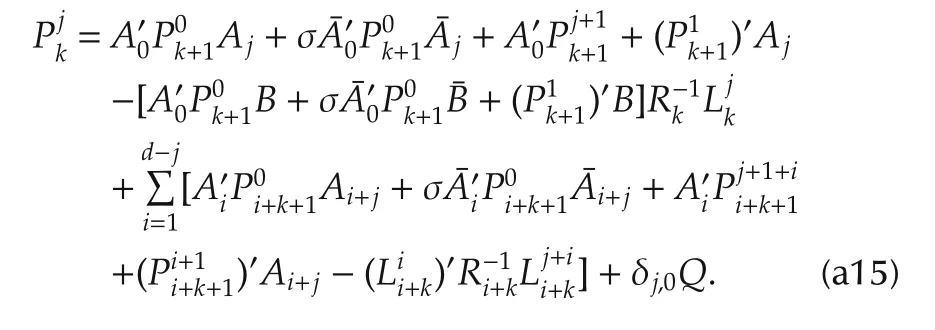
From(30),it follows

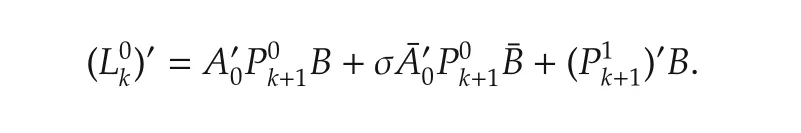
Employ the above equation in(a15).It leads to

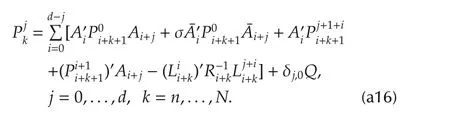
Now we show(42)and(43)fork=n-1.The following relation will be verified inductively ont=d,...,1:

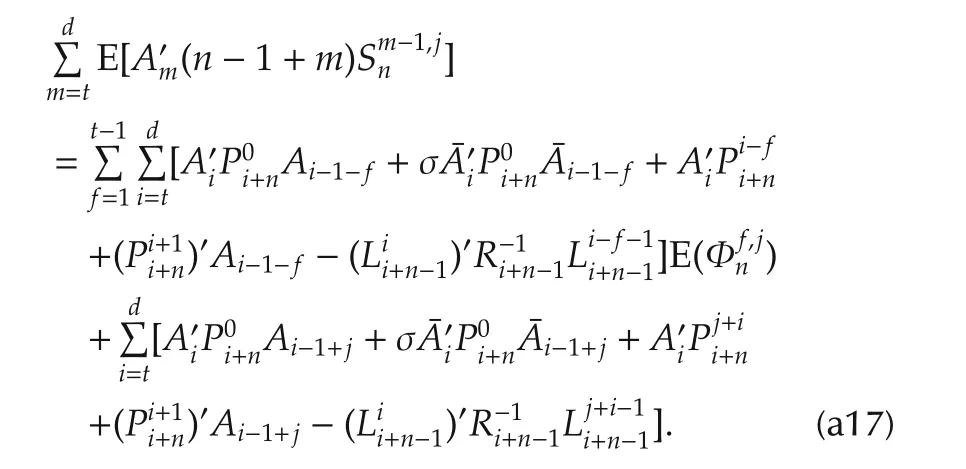
First,consider the case oft=d.In(32)and(31),settingk=nandm=dproduces

Substitution of(a18)into(a19)generates

which means

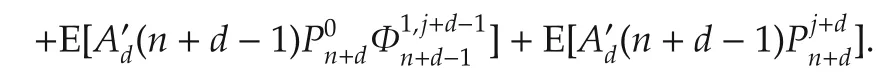
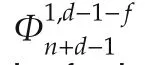
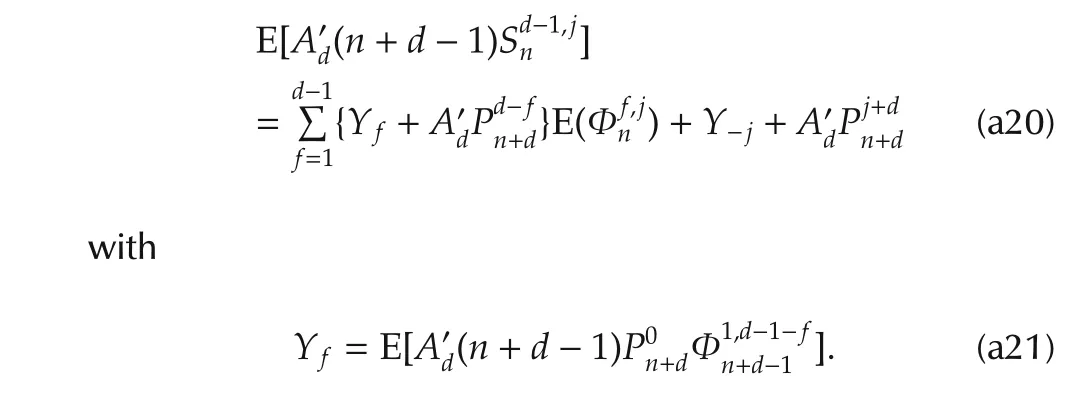
By applying(31)with k=n+d-1 and j=d-1-f in(a21),it results in

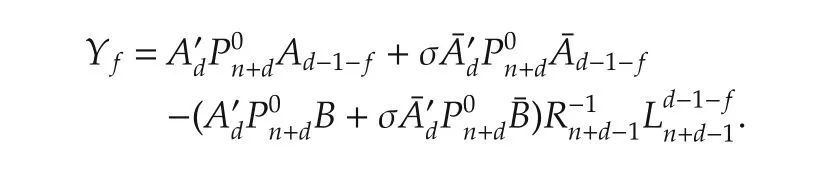
In view of(30),there holds

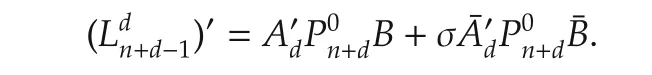
Therefore,Yfbecomes

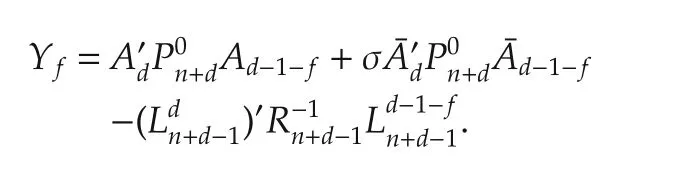
Y-jcan be obtained by replacing f with-j in the above equation.Employ Yfand Y-jin(a20).It yields

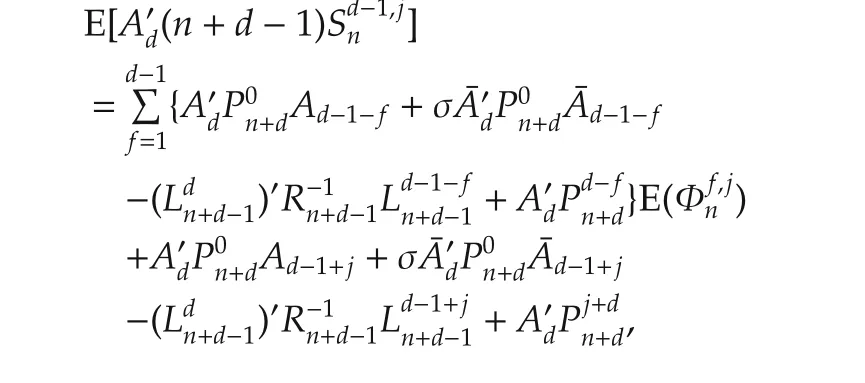
which is indeed(a17)for t=d.So far,the case of t=d has been clarified.

Suppose that(a17)holds for t=h+1 with 1≤h≤d-1,i.e.,

Now we show it is true for t=h.Note that

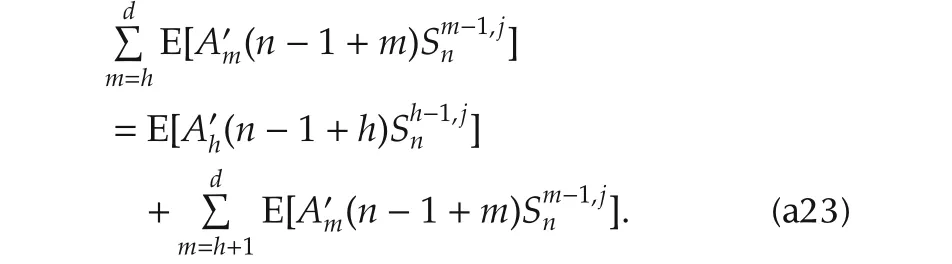
According to(32)and(31),Sh-1,jnand Φh,jnare respectively as

which yields

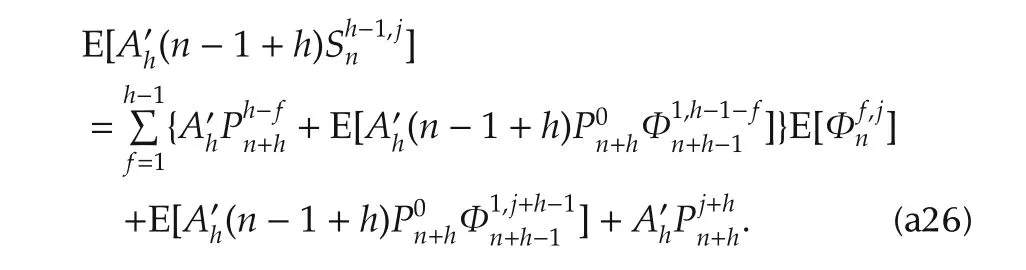
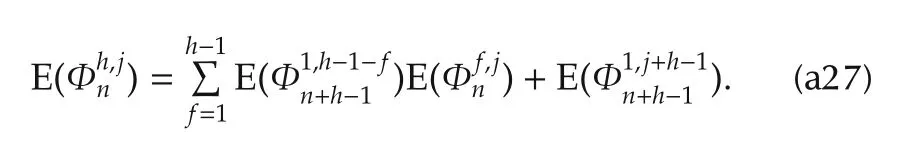
Combine(a22),(a23),(a26)and(a27).It results in

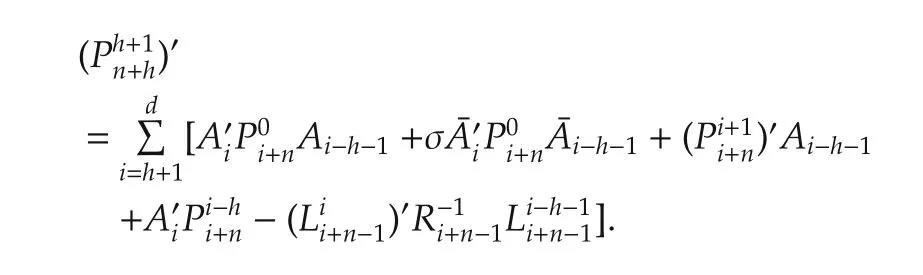
Apply the above equation in(a29).ThusYfbecomes

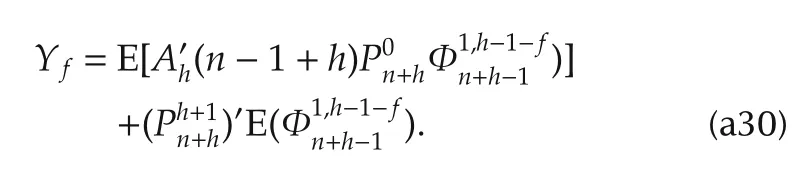
Furthermore,employ(31)and(30)in(a30).We get

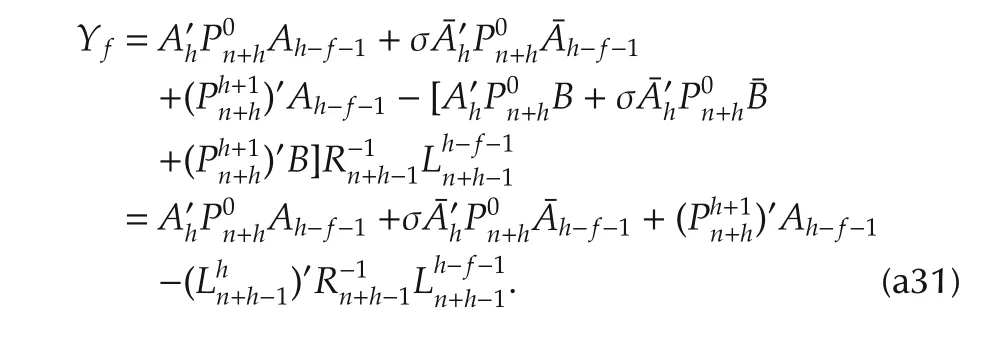
Replacingfwith-jin(a31)yieldsY-j.SubstituteYfandY-jinto(a28).Then(a17)fort=hcan be directly obtained.So far,it has been shown that(a17)is true fort=1,...,din an inductive way.In particular,settingt=1 in(a17)generates

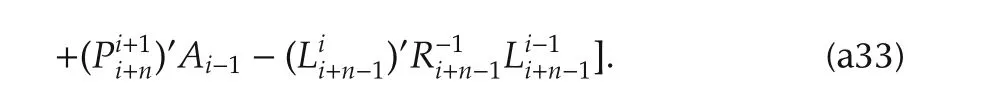
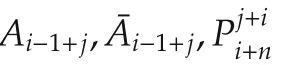
Huanshui ZHANGgraduated in Mathematics from the Qufu Normal University in 1986,and received his M.Sc.and Ph.D.degrees in Control Theory from Heilongjiang University,China,and Northeastern University,China,in 1991 and 1997,respectively.He worked as a postdoctoral fellow at Nanyang Technological University from 1998 to 2001 and Research Fellow at Hong Kong Polytechnic University from 2001 to 2003.He is currently a Changjiang Professorship at Shandong University,China.He held Professor in Harbin Institute of Technology from 2003 to 2006.He also held visiting appointments as Research Scientist and Fellow with Nanyang Technological University,Curtin University of Technology and Hong Kong City University from 2003 to 2006.His research interests include optimal estimation and control,time-delay systems,stochastic systems,signal processing and wireless sensor networked systems.E-mail:hszhang@sdu.edu.cn.

†Corresponding author.

E-mail:hszhang@sdu.edu.cn.

This work was supported by the Taishan Scholar Construction Engineering by Shandong Government and the National Natural Science Foundation of China(Nos.61120106011,61203029).

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg

the B.Sc.and M.Sc.degrees in Pure Mathematics from Shandong University,Jinan,Shandong,China,in 2008 and 2011,respectively.She is currently pursuing the Ph.D.degree in Control Theory and Engineering at Shandong University.Her research interests include optimalcontrol,stabilization,stochastic systems and time-delay systems.E-mail:linli_1987@163.com.