Topological structure and optimal control of singular mix-valued logical networks

2015-12-06YanWANGJunFENGMinMENG

Control Theory and Technology 2015年4期

Yan WANG,Jun-e FENG,Min MENG

School of Mathematics,Shandong University,Jinan Shandong 250100,China

Received 9 January 2015;revised 6 July 2015;accepted 23 July 2015

Topological structure and optimal control of singular mix-valued logical networks

Yan WANG,Jun-e FENG,Min MENG†

School of Mathematics,Shandong University,Jinan Shandong 250100,China

Received 9 January 2015;revised 6 July 2015;accepted 23 July 2015

This paper introduces singular mix-valued logical networks and singular mix-valued logical control networks.Via semi-tensor product,a singularmix-valued logicalnetwork can be converted to an algebraic form.On this basis,the normalization problem and solvability are discussed.Then,fixed points and cycles of singular mix-valued logical networks are also studied.Furthermore,the optimal control problem of singular mix-valued logical control networks is presented and a necessary condition for the existence of the optimal control is supplied,based on which,an algorithm is provided.Illustrative examples are given to show the feasibility of the results.

Singular mix-valued logical network,normalization problem,semi-tensor product,optimal control

DOI 10.1007/s11768-015-5007-4

1 Introduction

It is generally known that singular systems are widely used in many science and engineer systems and they are more effective than standard ones to describe practical systems,such as neural networks[6]and power network models.A singular Boolean network(SBN)is also called a dynamic-algebraic Boolean network.It has n-s certain algebraic equations and s dynamic models,which is same to many practical models,such as social networks.For SBNs,the fundamental problems,including normalization problems,solvability problems,limit sets,have been investigated in[7].However,forsingular mix-valued logical networks(SMLNs),these problems are still open.

On the otherhand,Shmulevich and Akutsu have studied the optimal control problem of Boolean networks and mix-valued networks in[8]and[9],respectively.However,recently,Cheng has presented a new matrix product,called semi-tensor product(STP)in[10],which is the basic tool in this article.By this approach,researchers have studied Boolean networks and obtained many useful results,such as model-input-state matrix,controllability and observability problem,stability analysis and stabilization,topological structure and the disturbance decoupling problem and optimal control for Boolean networks[11-17].For singular Boolean control networks,the optimal control problem has been well discussed via an analogous needle variation in[18].Using STP,the networked evolutionary games can be converted into Boolean networks and all of payoffs are in form of vectors[19].The problem of networked evolutionary games is to obtain the maximal payoff.It is noted that STP can also be applied to the mix-valued network[20]and via STP an SMLN or a singular mixvalued logical control networks(SMLCNs)can be converted into an algebraic form.In this paper,we further study the optimal control problem of SMLCNs by STP and give a necessary condition for the existence of optimal control.

We organize the rest of this paper as follows.Section 2 introduces some notations and several necessary results about STP.In Section 3,some preliminaries on dynamic-algebraic mix-valued logical networks are provided first.Then the normalization problem and solvability are studied.The SMLCNs and optimal control problem are discussed in Section 4.Also,in this section,we give an algorithm to calculate an optimal control and an illustrative example.Finally,Section 5 concludes this paper.

2 Notations and preliminaries

2.1 Notations

In this section,we introduce some notations first which will be used in the rest of this paper.All these notations can be found in[7]and[21].

▪Rm×n:the set of m × n real matrices.

▪x∈Dkexpresses that the logical variable x takes value from Dk.

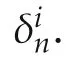
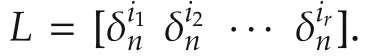
▪A logical matrix L= δn[i1i2···ir]is called a constant mapping matrix,if all the columns are the same,that is,i1=i2=...=ir.

▪Let A=(aij) ∈ Rm×n,B ∈ Rp×q.The Kronecker product of matrices A and B is defined as

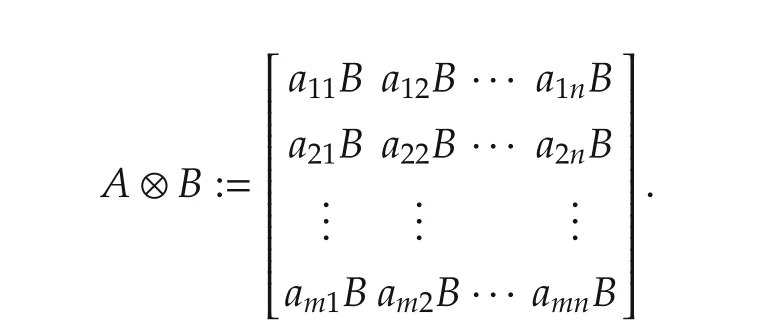
2.2 Preliminaries on STP

In this section,we will list some preliminaries on STP,which will be very useful in this article.

Def i nition 1[15] Let A ∈ Rm×nand B ∈ Mp×q.The STP of matrices A and B,denoted by A■B,is defined as

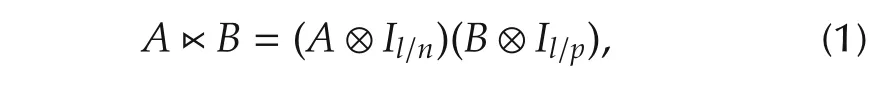
where l=LCM{n,p}is the least common multiple of n and p.

Remark 1If n=p,then the STP of matrices becomes the conventional matrix product.Thus,we can see that the STP is a generalization of the conventional product.

Def i nition 2[22] A swap matrix W[m,n]is an mn×mn matrix,defined as follows:label its columns by(11,12,...,1n,...,m1,m2,...,mn),label its rows by(11,21,...,m1,...,1n,2n,...,mn),and then the element at the position[(I,J),(i,j)]is

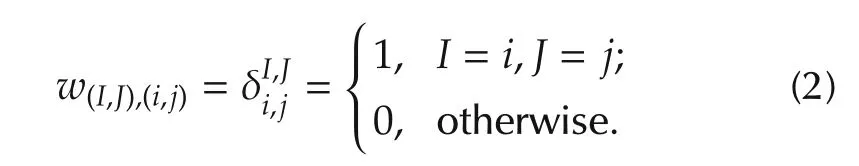
Lemma 1[4,22]1)Let X∈Rmand Y∈Rnbe two column vectors.Then

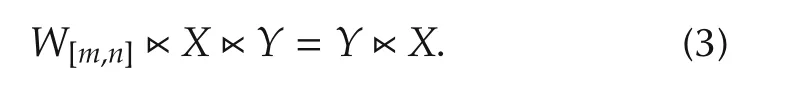
2)Given A ∈Rm×n,let Z ∈Rtbe a column vector.Then

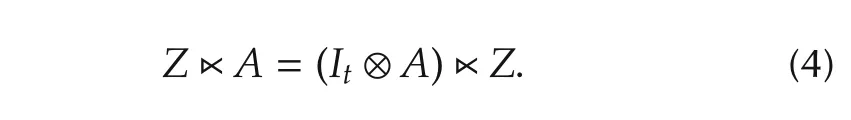
3)Let X∈Rn,Y∈Rqbe two column vectors and A ∈ Rm×n,B ∈ Rp×qbe two given matrices.Then

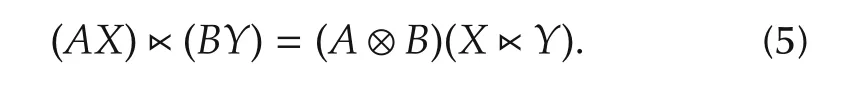
Furthermore,if X=Y∈Rn,n=q,then(5)becomes

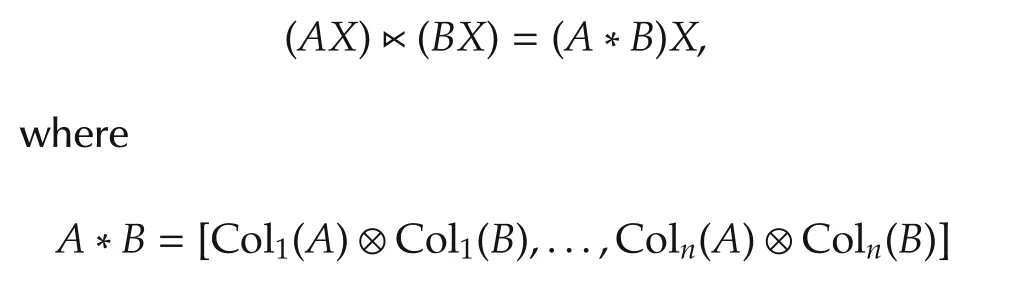
is the Khatri-Rao product of A and B.Readers can refer to[23]for the details of Khatri-Rao product.

4)Let xi∈Dki,i=1,...,n,be ki-valued logical variables.Then

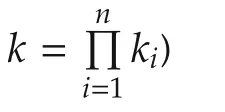
Here Lfis called the structure matrix of f.

5)Define an m order power reducing matrix Mr,mas

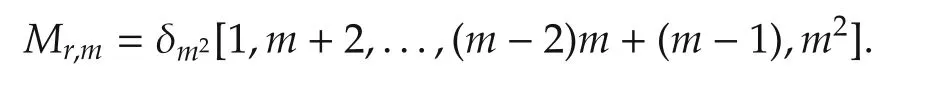
Then if X∈Δm,we can obtain X■X=Mr,mX.

3 Singular mix-valued logical networks

3.1 Description of singular mix-valued logical networks

First,we consider an SMLN with n nodes,which can be described as the following form([5]):

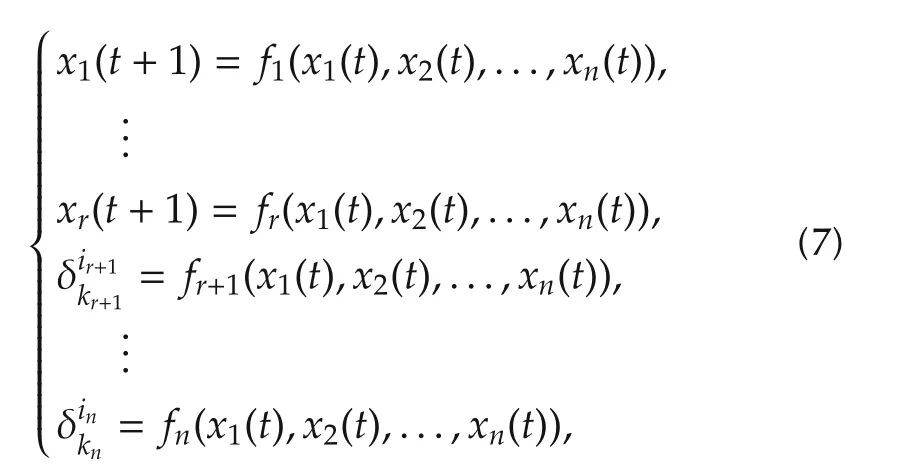
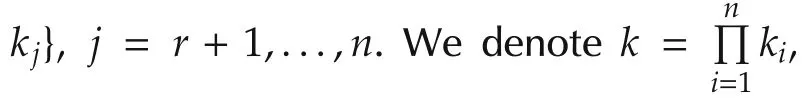
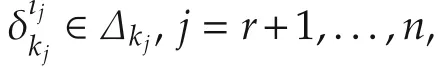
From 4)in Lemma 1,we can suppose that Fi∈ Lki×kis the structure matrix of fiin(8),i=1,...,n.

Then the equivalent form of(8)is

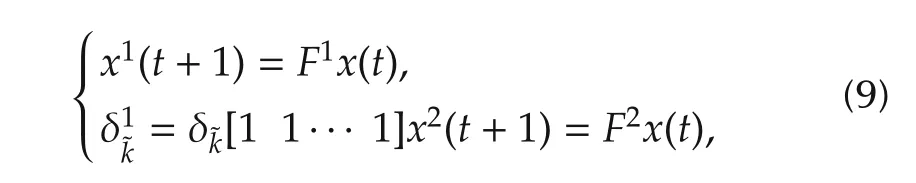
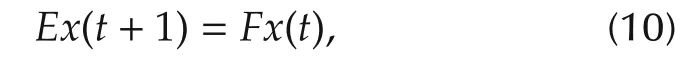
whereE=Iˆk⊗δ˜k[1 1···1]∈Lk×k,F=F1＊F2∈Lk×k.

Remark 2In equation(10),Eis a singular matrix.That is why we call(7)is an SMLN.

3.2 Normalization of singular mix-valued logical networks

3.2.1Problem statement

Consider a general SMLN with form of(10).Thus,we have

Def i nition 3Consider SMLN(11).The normalization problem is solvable,if we can find a coordinate transformationz=Txsuch that underzcoordinate frame,SMLN(11)is equivalent to the following mixvalued logical network:

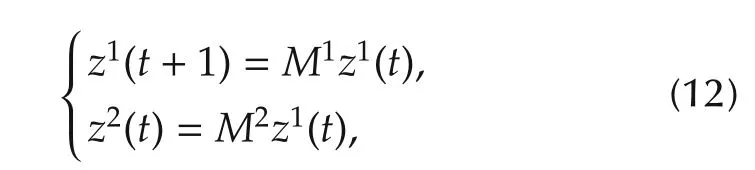
Thus,we can obtain the properties of(11)via studying those of(12).By this definition,we can solve the normalization problem in two steps:

1)Convert(11)into the following equivalent form:

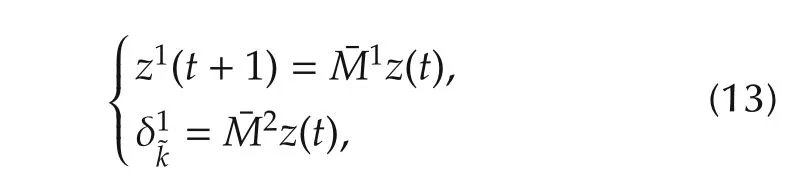
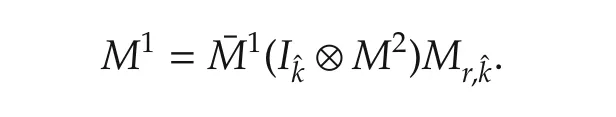
3.2.2Solvability of the normalization problem

Convert(11)into(13).

First we denote

Then we have the following result.

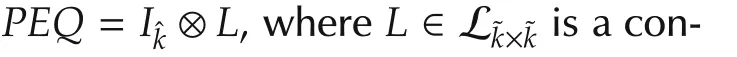
Thus,there are nonsingular matricesP,Q∈ Lk×ksuch that

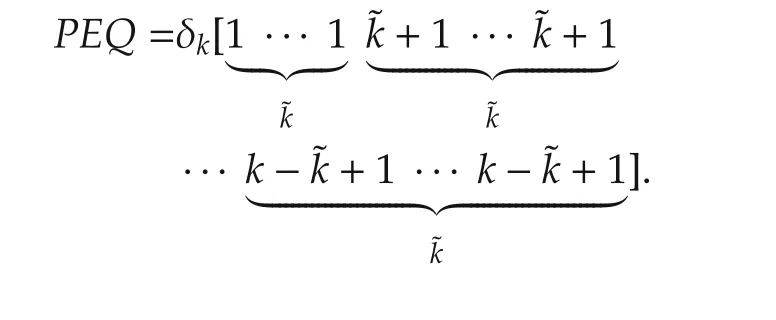
(Necessity)As we all know,fromEtoPEQ,what we have done is row permuting and column permutingE.Therefore,the number of 0 and 1 in any row ofEhas not been changed.We denote that

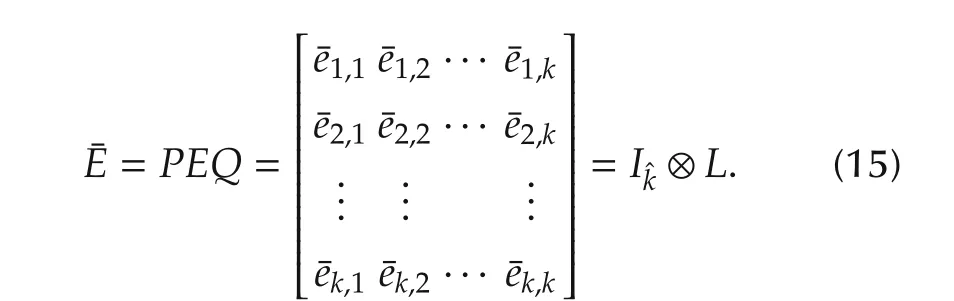
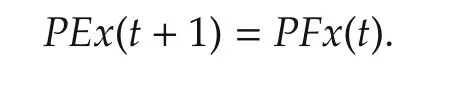
Take coordinate transformationz=QTxand we have

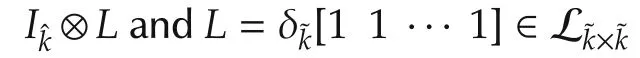
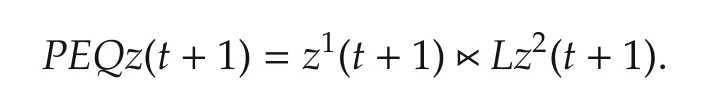
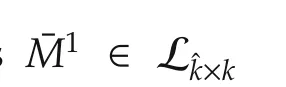
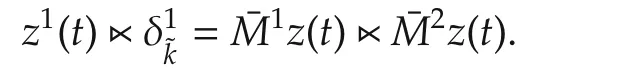
Therefore,(16)is equivalent to(13).From the discussions above,we have the following result.

This theorem gives the equivalent condition on that(11)converted into(13).Moreover,based on this,if we can give the condition on(13)into(12),then the solvability problem of SMLNs can be solved.

Convert(13)into(12).

First,we define a matrix set.

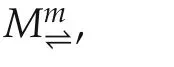
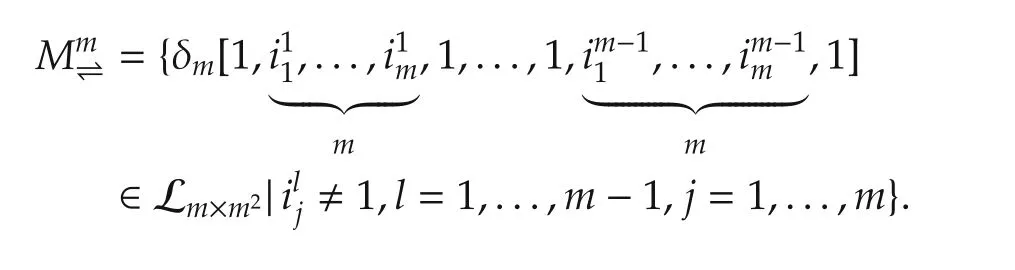
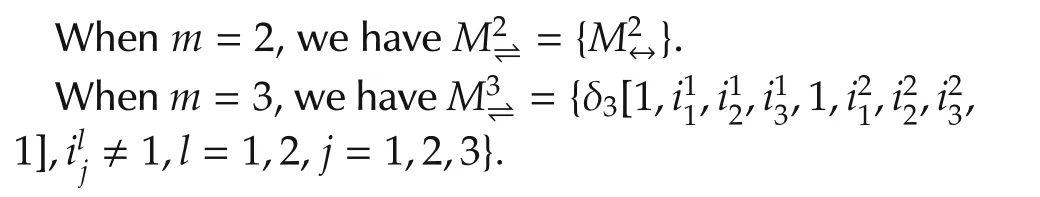
Then we give the following result.

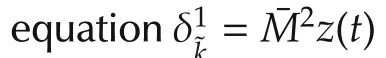
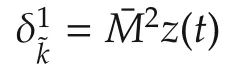
Example 1Consider an SMLN(11)with the following coefficients:

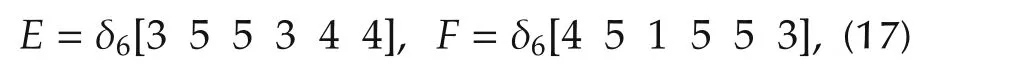
wherex(t)=x1(t)■x2(t),x1(t)∈ Δ3andx2(t)∈ Δ4.As we can see,Esatisfies the condition in Theorem 1.Setting

then we can obtain that

Then,under the coordinate transformationz=QTx,SMLN is converted into the following equivalent form:

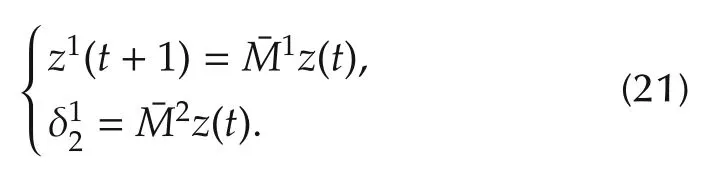
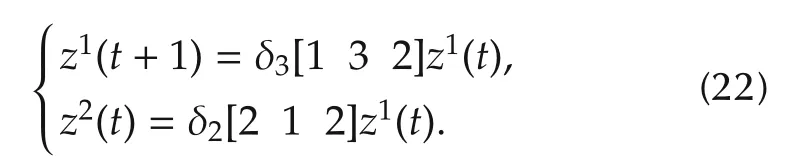
With simple calculation,we have

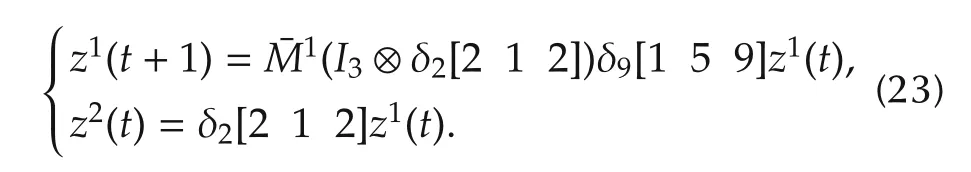
We solve the normalization problem of SMLN(11).

3.3 Solvability of singular mix-valued logical networks

In this section,we consider the solvability problem of SMLN(11).It is easy to get that SMLN(11)has a solution for any initial valuex(0),if and only if rank[E F]=rank[E].

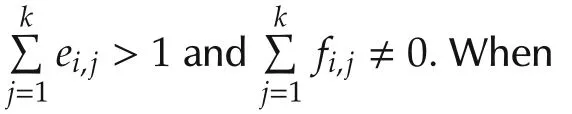
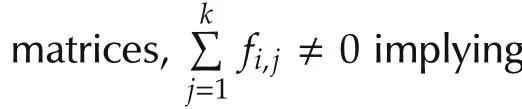
Fordiscussing the solution to SMLNwith form of(11),we introduce the admissible initial value.

IfSMLN(11)satisfies the condition ofTheorems 1 and 3,then(11)can be equivalently converted into(12).The set of admissible initial values of(12)can be defined as{z(0)=z1(0)z2(0):z2(0)=M2z1(0)},which is not empty.It is easy to know that(12)has a unique solution for any admissible initial value.Therefore,we obtain the following result.

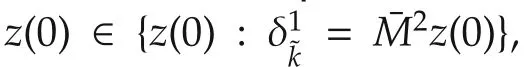
With this corollary and recalling Theorem 3,we obtain the following result.

Theorem 5For any admissible initial value,SMLN(13)has a unique solution,if and only if SMLN(13)can be equivalently converted into form(12).

3.4 Fixed points and cycles

In this section,we will discuss the fixed points and cycles of SMLN(11).First,we give the definition of fixed points and cycles for SMLN(11).

Def i nition 51)A statex0is called a fixed point of SMLN(11)ifEx0=Fx0.2){x0,x1,...,xp}is called a cycle of SMLN(11)with lengthpifxp=x0and the elements in the set{x0,x1,...,xp}are pairwise distinct.

In the sequence,we will provide a theorem to show how many fixed points an SMLN has.

Theorem 6For SMLN(11),δikis a fixed point,if and only if Coli(E)=Coli(F).That is,the number of fixed points of SMLN(11),which is denoted byNe,is equal to the number ofifor which Coli(E)=Coli(F),wherei=1,2,...,k.

ProofSuppose that δikis a fixed point of SMLN(11).Noting thatEδik=Coli(E)andFδik=Coli(F),we can easily obtain that δikis a fixed point if and only if Coli(E)=Coli(F). □

Remark 3For a general mix-valued logical networkx(t+1)=Lx(t),L=(li,j) ∈ Lk×k,we can also use the theorem above to determine a fixed point.δikis a fixed point if and only if Coli(Ik)=Coli(L),that is,li,i=1.Hence,the number of fixed points of this mix-valued logical network,denoted byNe,equals to the number ofifor whichli,i=1.That is,

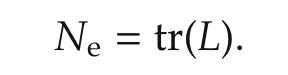
Remark 4If SMLN(11)can be normalized into(12),then the fixed points of(11)can be converted to those of(12)by transformation of coordinates.

According to the discussion above,we can derive the following result.

Corollary 2Suppose SMLN(11)can be normalized into(12),then the number ofifor which Coli(E)=Coli(F)is equal to tr(M1),whereM1=¯M1(Iˆk⊗M2)Mr,ˆk.Furthermore,if δikis a fixed point of SMLN(12),thenQδikis a fixed point of(11).

Similarly,if SMLN(11)can be normalized into(12),we can discuss cycles indirectly.Using the method presented in[15],we can first obtain all cycles of(12)and then those of(11).If{z0,z1,...,zp}is a cycle of SMLN(12),then{Qz0,Qz1,...,Qzp}is a cycle of(11).

Next,we will discuss cycles of a special class of SMLN without normalization.

Suppose that row(F)⊆row(E)for SMLN(11).Thus,there is a nonsingular matrixP∈ Lk×ksuch thatF=PE.DenoteEx(t)=y(t).Then equation(11)is equivalent toy(t+1)=Py(t).Using the method in[15],we can get cycles of this equivalent equation.For a cycle{y0,y1,...,yp}ofy(t+1)=Py(t),ifyi∈Col(E),i=0,1,...,p,then we can get a cycle{x0,x1,...,xp}of(11)corresponding to{y0,y1,...,yp}.Thus,if there is someyithat does not belong to Col(E),then there is no cycle of(11)corresponding to{y0,y1,...,yp}.Finally,for cycles of length 2 of SMLN,we have the following result.

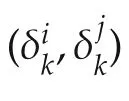
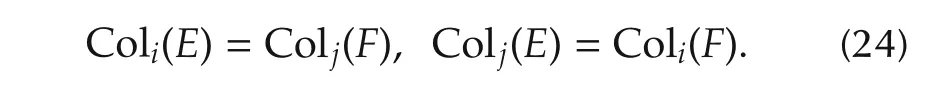
From this theorem,the numberofcycleswith length 2 of SMLN(11),denoted byN2,is equal to the number of pair(i,j)for which Coli(E)=Colj(F),Colj(E)=Coli(F).

It is easy to see that Theorem 7 can be extended to theslength case.

Example 2Recall Example 1.

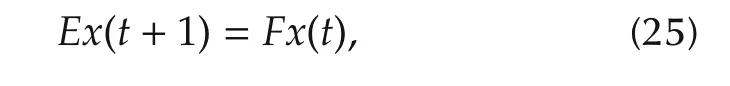
whereE= δ6[3 5 5 3 4 4]andF= δ6[4 5 1 5 5 3].We have already known that SMLN(25)can be normalized into the following form:

DenoteM1= δ3[1 3 2]andM2= δ2[2 1 2].Using the method presented in[15],we can obtain the fixed points and cycles of the first equation in(26).We can easily obtainNe=tr(M1)=1.Additionally,we have tr(M21)=3 and tr(M31)=1.With further calculation,we can see that this SMLN has one fixed point and one cycle with length 2.Noting that Col1(M1)= δ13,that is,δ13is the fixed point of the first equation in(26).Substitute it into the second equation of(26),we can obtain the fixed point of(26)isz0=δ26.Sincex=Qz,the fixed point of(25)isx0=δ26.Similarly,we can obtain the cycle of(26)is(δ36,δ66).Thus,under transformation,the cycle of(25)is(δ16,δ66).

4 Singular mix-valued logical control networks and optimal control problem

In this section,we will discuss SMLCNs and the optimal control.

4.1 Singular mix-valued logical control networks

Similar to SMLNs,we can consider an SMLCN withnnodes as the following form:

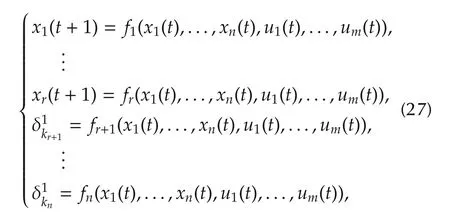
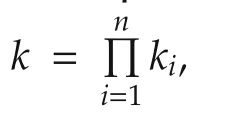
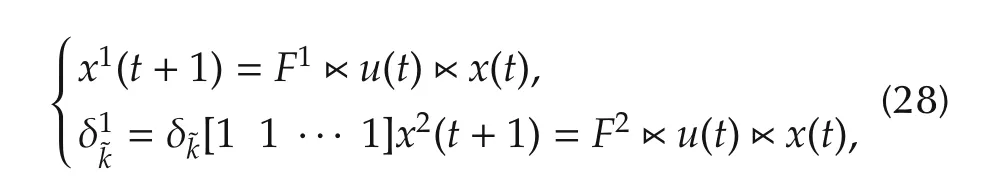
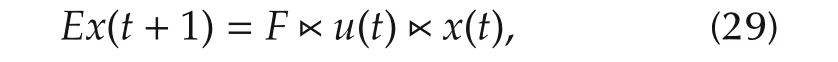
whereE=Iˆk⊗δ˜k[1 1···1]∈Lk×k,F=F1＊F2∈Lk×kq.

By Theorem 5,we have the following result.

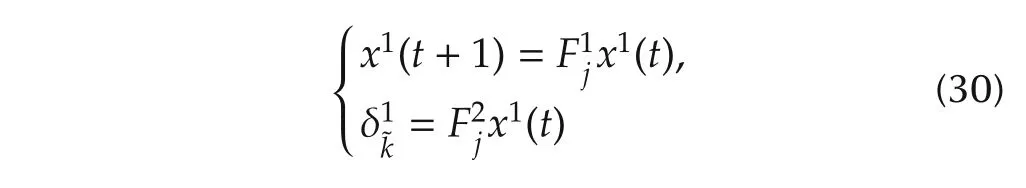
is equivalent to

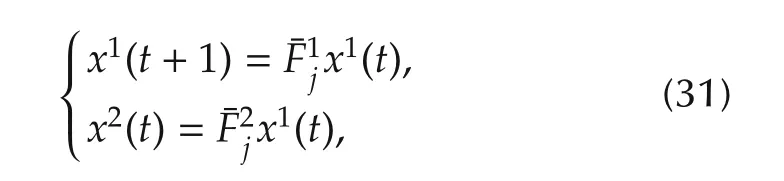
wherej=1,2,...,q.

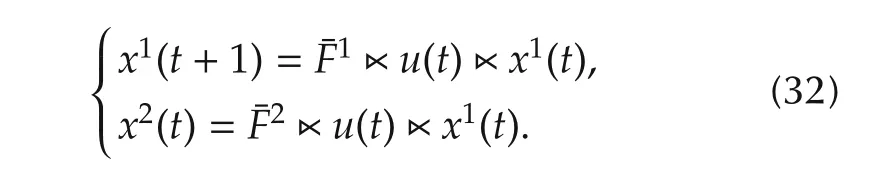
4.2 Optimal control problem

Consider an SMLCN in the form of(28).The optimal controlproblem isto determine a controlthatmaximizes(or minimizes)the given cost-functional.

Assume thatN＞0 is a terminal time.Denote U={{u(0),u(1),...,u(N)}:u(t)∈ Δq,t=0,1,...,N}.For a controlu(t),x(t;u)means the solution to(28)at timetwith the initial valuex(0)=x0.Define the costfunctional as

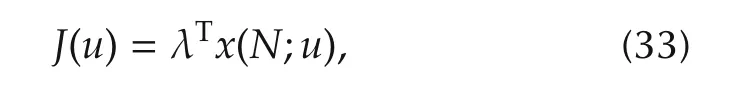
where λ∈Rkis a given column vector.The problem we need to solve is to choose a controlu＊∈ U that maximizesJandu＊is the optimal control here.

To solve the optimal control problem of(28),we should ensure that with any controlu,(28)has a unique solution for any admissible initial value.Therefore the optimal control problem of(28)is equivalent to that of(32).Noting the first equation of(32),for anyp≤t,we have

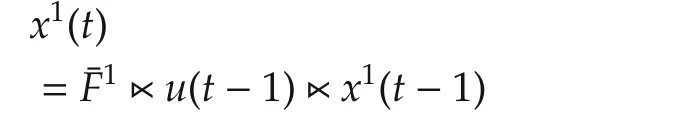
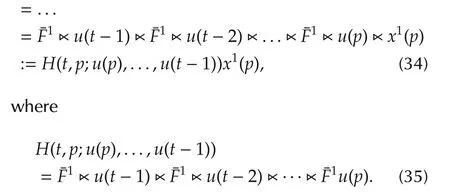
Ifp=t,we haveH(t,p;u(p),...,u(t-1))=Iˆk.

From(35),for anyp≤l≤t,we can obtain that

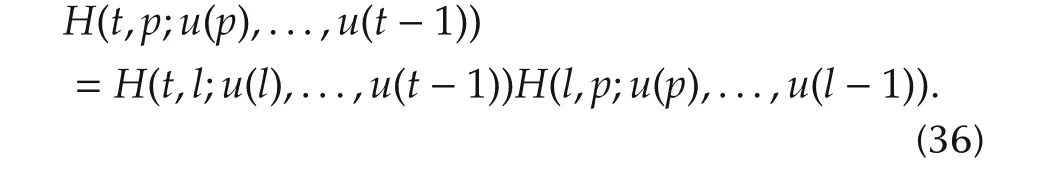
Then we have the following result,which is important in this section.

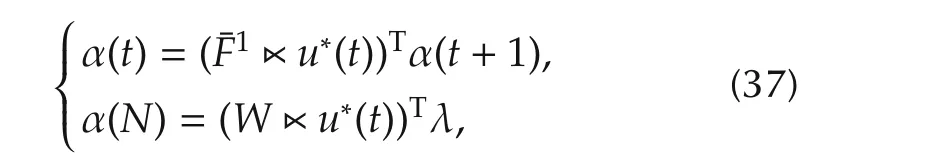
and functions βi:{0,1,...,N}→ R as

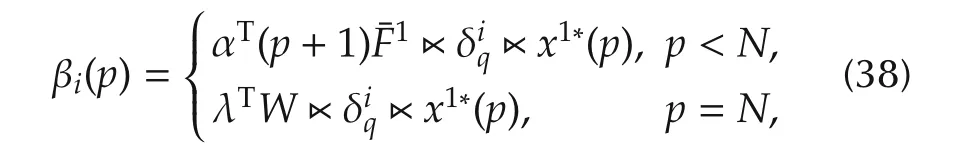
wherei=1,2,...,N,and

With any integerp∈{0,1,...,N},if fori,there exists βi(p)＞ βj(p)for anyj≠i,thenu＊(p)= δiq.

ProofFirst of all,we denote a new controlu∈U as

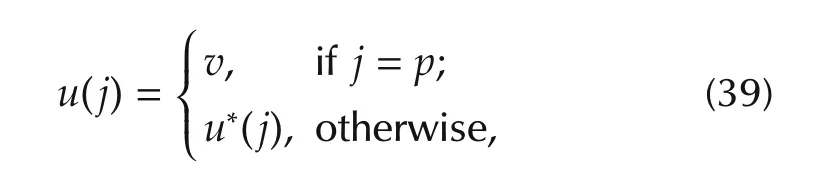
wherep∈{0,1,...,N}is a given arbitrary integer andv∈Δqis an arbitrary vector.From the definition above we can see thatuis always equivalent tou＊except at the timep.Denote the solution with respect to controlu＊asx＊(t),that isx＊(t)=x(t;u＊).Next,we first determine the optimal control at timeN:u＊(N),and then at other times:u＊(j),j=0,1,...,N-1.

1)Ifp=N,

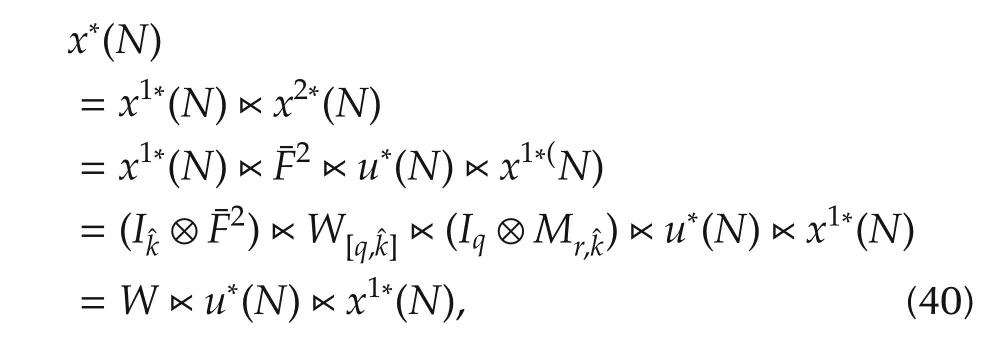
and then similarly,

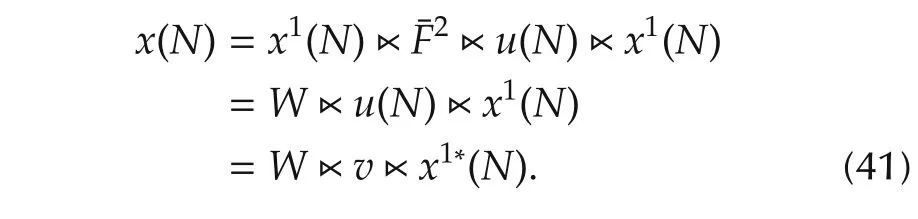
Thus,we have

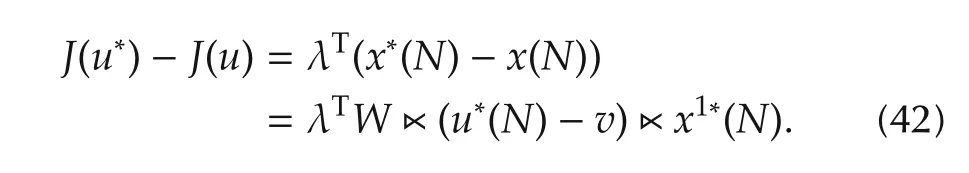
Assuming that for allj=1,2,...,q,there exists an integeri∈ {0,1,...,q},i≠j,such that βi(N)＞ βj(N).Next we need to proveu＊(N)= δiq.Otherwise,ifu＊(N)≠ δiq,we can suppose thatu＊(N)= δjqifj≠i.Letv= δiq.Then we have

which contradicts the fact thatu＊is an optimal control.Therefore,we complete the proof thatu＊(N)= δiq.

2)Ifp＜N,

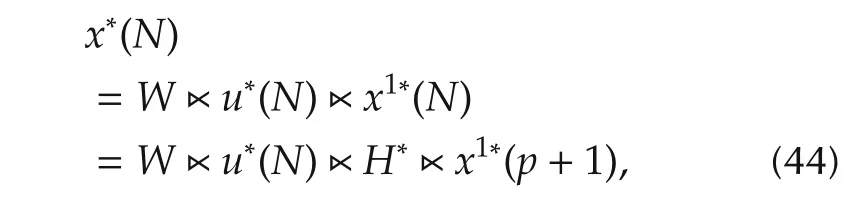
whereH＊=H(N,p+1;u＊(p+1),...,u＊(N-1)),and we similarly have

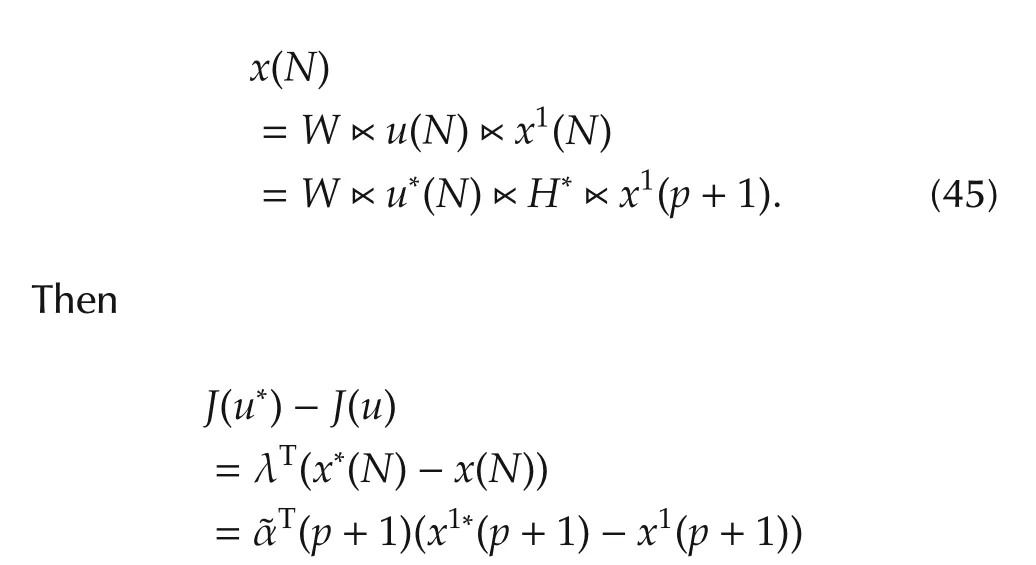
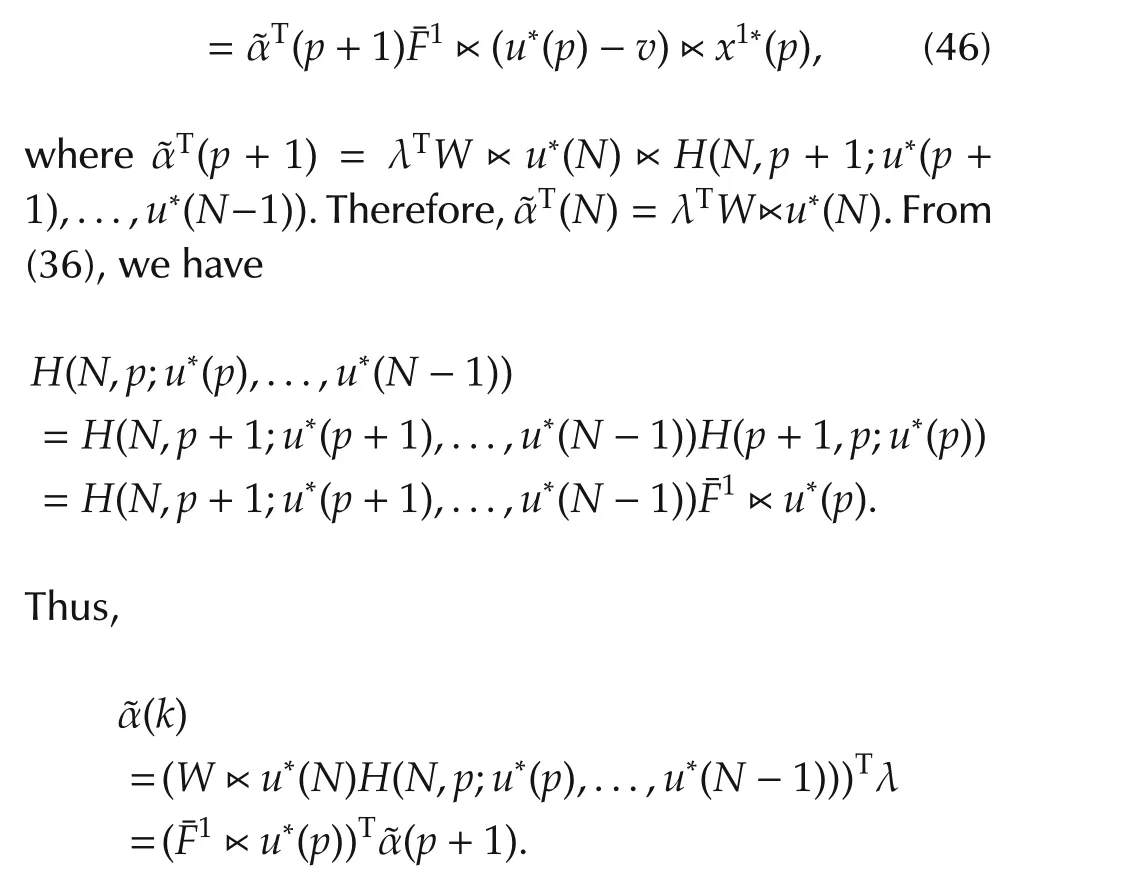
Considering equation(37),we take˜α(p)=α(p),p=0,1,...,N.Thus,

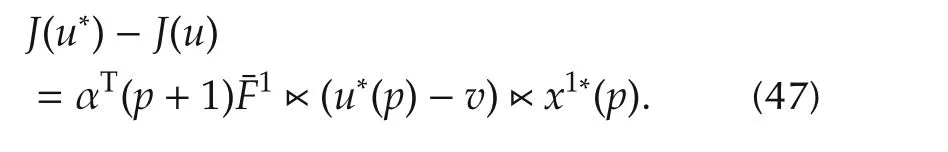
Now,suppose that for allj=1,2,...,qandj≠ithere exists an integeri∈ {0,1,...,q}such that βi(N)＞ βj(N).Therefore,similar to 1),we can prove thatu＊(p)= δiq.We complete the proof. □

Next,we present two special cases.

Remark 51)Ifki=qj=2,i=1,2,...,n,j=1,2,...,m,SMLCN(28)becomes a singular Boolean control network.When it satisfies the conditions in Theorem 8,the optimal control isu＊= δi2m.The result is same to Theorem 1 in[18].

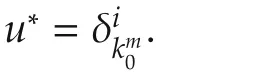
Remark 6If there is no integerisatisfying the condition that βi(p) ＞ βj(p)for allj≠i,Theorem 8 will lose its feasibility.While in fact,we can always find a set{i1,i2,...,is}⊂ {1,2,...,q}such that βi1(k)= βi2(k)=...= βis(k)＞ βj(k)forallj∉S.DenoteS={i1,i2,...,is}.On this basis,denote

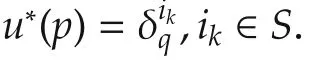
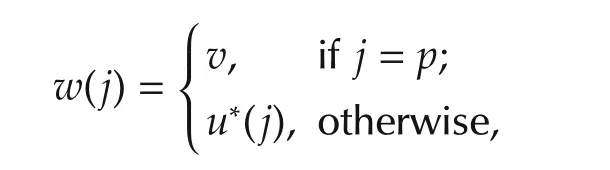
From the proof of Theorem 8 and Remark 6,we can provide an algorithm to determine an optimal control.

Algorithm 1Assume thatNis the final time andJ(u)=λTx(N;u)is the given cost-functional.Then,we can present the following steps to calculate the optimal controlu＊={u＊(0),u＊(1),...,u＊(N)}.

1)Calculate the matrixWpresented in Theorem 8.

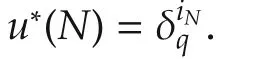
3)Calculate α(N)in(37).Setp=N-1.

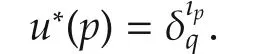
5)Ifp=0,stop.Otherwise,setp:=p-1 and return to Step 4).

Finally,the optimal control

can be determined.

4.3 An illustrative example

In this section,we will provide an illustrative example to show the feasibility of Theorem 8.

Example 3Consider the following SMLCN with three nodes:

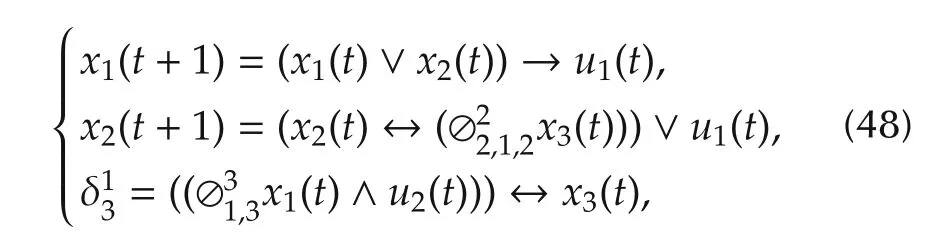
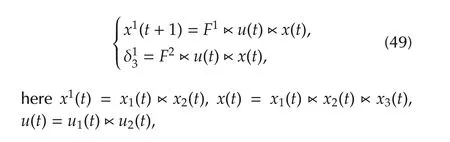
From equation(48),we know that the third equation is equivalent tox3(t)=⊘31,3x1(t)∧u2(t).Therefore,the algebraic form of(48)can also be written as

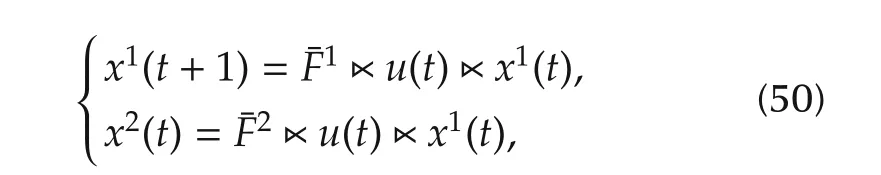
where,x2(t)=x3(t),

With simple calculation and from Theorem 8,we can obtain that

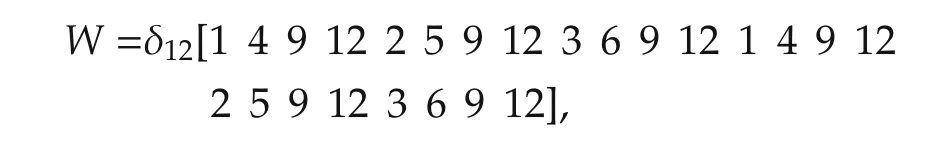
and the functions that we have defined

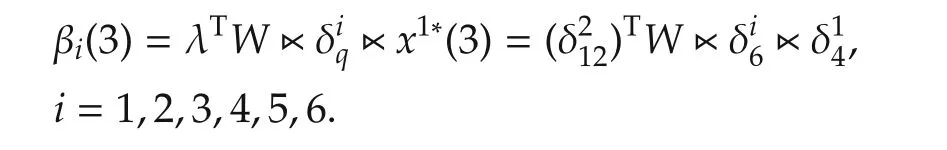
We can easily derive that

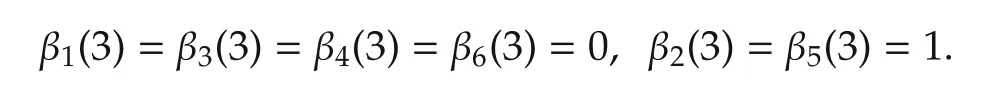
Thus,we have u＊(3)= δ26or δ56.Take u＊(3)= δ26,then we have

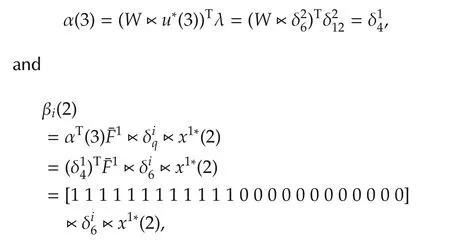
where i=1,2,3,4,5,6.It is easy to obtain that

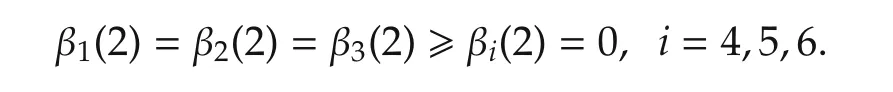
Thus,u＊(2)= δ16or δ26or δ36.Take u＊(2)= δ16.In this case,

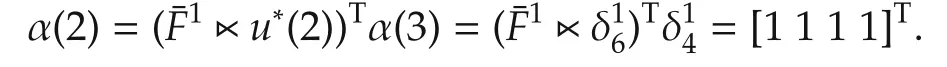
And then

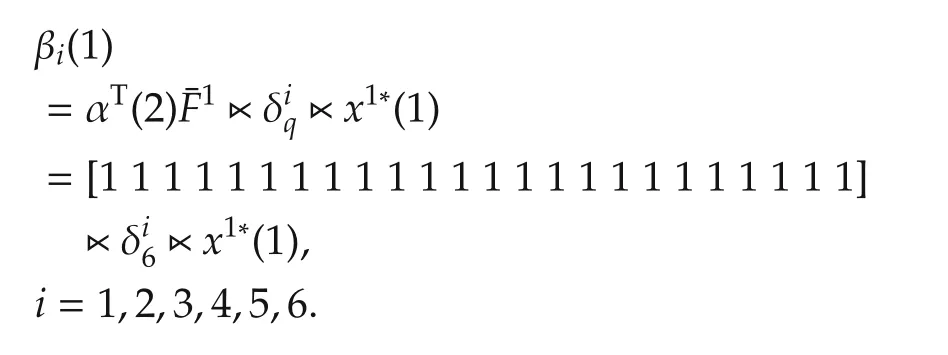
With simple calculation,we have

Therefore,u＊(1)∈ {δ16,δ26,δ36,δ46,δ56,δ66}.Take u＊(1)= δ16,and

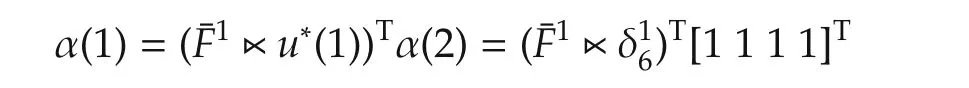
We can similarly obtain that u＊(0)∈ {δ16,δ26,δ36,δ46,δ56,δ66}.Take u＊(0)= δ16.Finally,we find an optimal control as

As a matter of fact,the optimal control is not unique.For instance,if v ∈ {δ16,δ26,δ36,δ46,δ56,δ66},{v,δ16,δ16,δ26}is an optimal control too.

On the other hand,with the admissible initial value x1(0)=x2(0)=x3(0)=0 and the optimal control

the solutions of the SMLCN(48)are

At this very moment,J(u)= λTx(3;u＊)=1.Thus,u＊is optimal.

5 Conclusions

SMLNs have been introduced and the optimal control problem of SMLCNs has been investigated.Via STP and the algebraic form,we have discussed the normalization problem.Moreover,the existing and unique property of solutions of SMLNs and SMLCNs has been investigated.We also have considered fixed points and cycles of SMLNs.Then,we have provided a necessary condition for the existence of optimal control of SMLCNs,which also holds for singular Boolean and k-valued logical control networks.Besides,we have given an algorithm to calculate the optimal control.This paper is the first research to propose SMLNs and SMLCNs.The results that we obtain are more generalthan thatofsingular Boolean control networks and singular multi-valued logical networks.When ki=qj=2,the results degenerate into that of Boolean networks and when ki=qj=k0＞2,the results degenerate into multi-valued case.

[1]S.Kauffman.Metabolic stability and epigenesis in randomly constructed genetic nets.Journal of Theoretical Biology,1969,22(3):437-467.

[2]D.N.Arnosti,A.Ay.Boolean modeling of gene regulatory networks:Driesch redux.Proceedings of the National Academy of Sciences of the United States of America,2012,109(45):18239-18240.

[3]K.E.Kurten.Correspondence between neuralthreshold networks and Kauffman Boolean cellular automata.Journal of Physics A:Mathematical and General,1988,21(11):615-619.

[4]D.Cheng,X.Xu.Bi-decomposition of multivalued logical functions and its applications.Automatica,2013,49(7):1979-1985.

[5]D.Cheng,Y.Zhao,X.Xu.Mix-valued logic and its applications.Journal of Shandong University(Nature Science),2011,46(10):32-44.

[6]V.B.Bajic.Lyapunov’s Direct Method in the Analysis of Singular SystemsandNetworks.RSA:Shades TechnicalPublications,1992.

[7]J.Feng,J.Yao,P.Cui.Singular Boolean networks:Semi-tensor product approach.Science China Information Sciences,2013,56(11):1-14.

[8]I.Shmulevich,E.R.Dougherty,W.Zhang.From Boolean to ptobabilistic Boolean networks as models of genetic regulatory networks.Proceedings of the IEEE,2002,90(11):1778-1792.

[9]T.Akutsu,M.Hayashida,W.Ching,et al.Control of Boolean networks:Hardness results and algorithms for tree structured networks.Journal of Theoretical Biology,2007,244(4):670-679.

[10]D.Cheng.Semi-tensorproductofmatrices and its applications-a survey.Proceedings of the 4th International Congress of Chinese Mathematicians,Beijing:Higher Education Press,2007:641-668.

[11]L.Zhang,J.Feng,M.Meng.MIS approach analyzing the controllability of switched Boolean networks with higher order.International Journal of Control,Automation and Systems,2014,12(2):450-457.

[12]L.Zhang,J.Feng,J.Yao.Controllability and observability of switched Boolean control networks.IET Control Theory&Applications,2012,6(16):2477-2484.

[13]D.Cheng,H.Qi,Z.Li,et al.Stability and stabilization of Boolean networks.International Journal of Robust and Nonlinear Control,2011,21(2):134-156.

[14]Y.Zhao,Z.Li,D.Cheng.Optimal control of logical control networks.IEEE Transactions on Automatic Control,2011,56(8):1766-1776.

[15]D.Cheng,H.Qi,Z.Li.Analysis and Control of Boolean Networks:A Semi-tensor Product Approach.London:Springer,2011.

[16]M.Meng,J.Feng.Topological structure and the disturbance decoupling problem of singular Boolean networks.IET Control Theory and Applications,2014,8(13):1247-1255.

[17]M.Meng,B.Li,J.Feng.Controllability and observability of singular Boolean control networks.Circuits,Systems and Signal Processing,2015,34(4):1233-1248.

[18]M.Meng,J.Feng.Optimal control problem of singular Boolean control networks.International Journal of Control,Automation,and Systems,2015,13(2):266-273.

[19]D.Cheng,H.Qi,F.He,et al.Semi-tensor product approach to networked evolutionary games.Control Theory and Technology,2014,12(2):198-214.

[20]D.Cheng,Y.Zhao.Normal form of general logic mappings.Proceedings of the 30th Chinese Control Conference.Yantai,China:IEEE,2011:6368-6373.

[21]Q.Si,J.Feng,J.Yao,et al.The normalization and solvability of singular multi-valued networks.Proceedings of the 33rd Chinese Control Conference.Nanjing,China:IEEE,2014:2799-2804.

[22]D.Cheng,H.Qi.Semi-tensor Product of Matrices-Theory and Applications.Beijing:Science Press,2007(in Chinese).

[23]L.Ljung,T.Soderstrom.Theory and Practice of Recursive Identification.Cambridge:MIT Press,1983.

Yan WANGis a postgraduate student and pursuing for the M.Sc.degree at Shandong University.Her research interests include Boolean networks,mix-valued networks and semi-tensor product.E-mail:wangyansdu@126.com.

the Ph.D.from Shandong University in 2003.She is currently a professor of School of Mathematics in Shandong University,Jinan,China.Her research interests include singular systems,fuzzy systems and logic control networks.E-mail:fengjune@sdu.edu.cn.

MinMENGreceived the B.Sc.degree and Ph.D.from Shandong University in 2010 and 2015,respectively.Her research interests include Boolean networks,positive linear systems and semi-tensor product.E-mail:mengminmath@gmail.com. — ——-— ——

†Corresponding author.

E-mail:mengminmath@gmail.com.

This work was partially supported by the National Natural Science Foundation of China(No.61374025)and the Excellent Youth Foundation of Shandong Province(No.JQ201219).