应用NLOS鉴别补偿的无线传感器网络TDOA定位算法

杨北亚，熊 辉，丁 宏，胡 婷，杨 锋

(1.国防科学技术大学电子科学与工程学院，长沙 410073;2.兰州交通大学电子与信息工程学院，兰州 730070)

随着社会各个行业对于无线定位需求的日益增多，国内外掀起了一股无线定位技术研究的热潮［1－6］。目前的无线传感器节点测距方法有基于到 达 信 号 强 度(RSSI)［7］、到达信号角度(AOA)［7］、信号到达时间(TOA)［8］、信号到达时间差(TDOA)［9］等方法。其中基于时间的 TDOA节点测距方法因测距精度较高、稳定性好、对设备的要求较低等优点，成为目前传感器定位的主流算法。

在无线传感器网络系统中，定位误差的来源主要有2个方面:① 信道环境不佳造成的测量误差;② 由于定位方程非线性造成的计算误差［10］。其中，非视距(NLOS)因素是测量误差中重要的组成部分。经典的定位算法如 Chan［11］、Taylor级数展开法［12］等都未考虑NLOS对于定位的影响，在锚节点存在非视距情况的环境中这2种方法性能不佳。因此，消除非视距因素造成的影响从而提高定位精度对理论研究和工程应用都具有重要意义。

目前国内外对于非视距误差的处理主要分为2种形式:一种是通过计算权重的方式抑制非视距误差的影响，例如，残差加权法［13］通过对节点测距的冗余结果进行加权从而抑制非视距误差的影响。该方法需要较多的锚节点参与定位，同时需要视距情况下的先验信息，因此在较为恶劣的环境中不易实现。另一种方法直接在测量TOA信息中减去非视距误差。Wylie等［14］提出的重构法利用视距(LOS)情况下的先验信息，对NLOS误差进行校正，消去NLOS误差对于测距的影响。该方法同样需要LOS情况下的先验信息，在较为恶劣的环境中难以实现。

考虑到传统方法依赖先验信息这一情况，本文提出了一种改进的方法。首先，在实际定位系统中，锚节点之间的通视很容易做到，因此假定锚节点之间通视，通过锚节点与锚节点之间的测量TOA信息所计算出的TDOA信息得到TDOA参考均方差;其次，利用多组锚节点与标签之间的测量TOA信息计算对应锚节点之间的TDOA信息，并统计均方差，将其与参考均方差进行比对，筛选出具有非视距的锚节点，并剔除该锚节点的TOA信息，从而消除非视距误差的影响。同时，当视距锚节点数不能满足较高的定位要求时，可利用非视距误差的分布特性估计并补偿TDOA信息，以此消除或降低非视距的影响，达到精确定位的目的。

本文的主要思路:①通过鉴别算法找出存在非视距误差的锚节点，并剔除该锚节点的TOA信息;②利用已判断的通视锚节点预估标签位置信息;③利用非视距时延量在特定信道环境下服从特定分布的特性及通视锚节点预估的标签位置信息计算出非视距时延，并对TDOA信息进行补偿，抑制非视距因素对定位性能的影响;④ 通过最大似然及牛顿迭代法完成最终的标签位置信息估计。

1 非视距误差的鉴别与估计

1.1 定位模型的建立

基于TDOA的定位技术是通过检测信号到达不同锚节点的时间差来确定标签位置信息的一种定位技术。当标签广播信号时，由于多个锚节点与标签之间的距离不等，因此不同的锚节点接收该信号时会产生一个时间差。使用标签与多个锚节点之间的测量TOA信息，相减得到TDOA信息。同时，由于电磁波在相同介质中的传输速率相同，故通过多组TDOA信息可得到锚节点与标签之间的距离信息，并通过各类定位算法计算出标签的位置信息，最终达到定位的目的。

如图1为无线传感器网络定位系统的实现结构，其中有N个位置已知的锚节点，锚节点4与标签之间出现了非视距的情况。

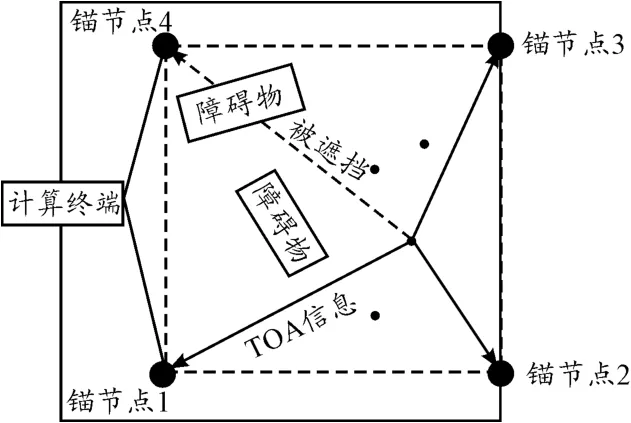
图1 无线传感器网络定位系统架构

1.2 非视距误差鉴别算法

为了辨别定位系统中是否存在非视距锚节点，需要利用特定算法进行鉴别。Wylie等［14］提出的重构法是鉴别算法的典型代表。但该算法需求出锚节点视距情况下的先验信息，而在实际使用中往往很难获得锚节点的先验信息，因此需要在没有先验信息的情况下鉴别出含有非视距误差的锚节点。

定位系统中，锚节点j与标签之间在ti时刻测量的TOA信息可以表示为

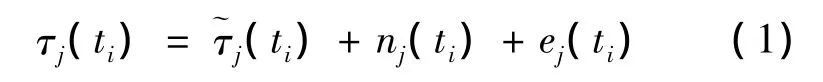
其中:τj(ti)表示系统测量的TOA信息;表示真实的TOA值;nj(ti)表示系统测量的误差，服从均值为0、方差为的高斯分布;ej(ti)表示锚节点j与标签之间由于非视距所造成的时延量，均值为μe，j，方差为。由于非视距时延与测量噪声在时间上不相关，故可以推断出:有非视距时延存在的测量TOA信息必然有一个大于无非视距误差的TOA信息的均方差。但在实际定位系统中，标签广播信号的时间间隔不可忽略。由于测量TOA信息中包含该时间间隔变量，因此无法直接使用统计的TOA测量信息进行对比。

本文提出了一种改进的思想:假定锚节点位置信息已知且互相通视(锚节点之间通视易于实现)，锚节点之间时钟同步。在系统定位过程中，利用锚节点之间通信的TOA信息计算锚节点之间的TDOA信息，统计TDOA信息均方差，得到一个参考值σa。同时，多次测量并记录各个锚节点与标签之间的TOA信息，计算相应的TDOA信息，统计对应TDOA信息的均方差［σ1，2σ1，3…σN，N－1］，其中:σ1，2表示锚节点1与锚节点2之间TDOA信息的均方差;N表示锚节点个数。依据非视距误差存在与否时TDOA信息均方差的变化特性，分别将［σ1，2σ1，3… σN，N－1］与参考值 σa进行对比，若 σN，N－1接近参考值或等于参考值，则这2个锚节点都无非视距情况;若σN，N－1远大于参考值，则这2个锚节点中至少有一个存在非视距情况。此时继续选择锚节点N－1进行对比，直到筛选出所有非视距锚节点，完成非视距锚节点的剔除。

若筛选完成后，能通视的锚节点数不足以满足较高的定位精度，则可使用以下非视距误差时延量估计的方法对非视距误差进行补偿，在消除部分非视距的影响后再进行定位。

1.3 非视距造成时延量的估计

当存在非视距误差时，可近似认为在不同信道环境下非视距误差服从指数分布、均匀分布与Delta分布［15］。近似认为其服从指数分布，其概率密度函数为:

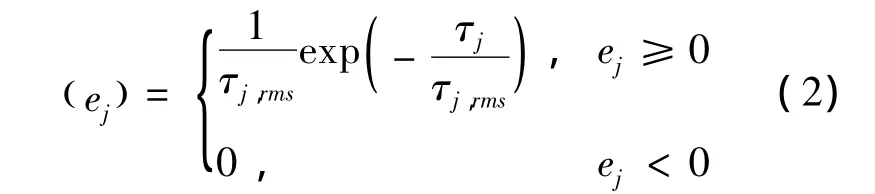
其中:τj，rms为由信道环境决定的均方根时延扩展，可表示为表示不同信道环境下在d=1 km处的延时扩展的中值;dj表示锚节点j与标签之间的距离;ε取0.5到1之间的常数;c表示服从均值为0、方差为σc=4 dB的对数正态分布的随机变量。本文考虑在都市环境中的情况，系数a取1 μs。因为c服从对数正态分布，且a与d都不是随机变量，故 τj，rms应服从对数正态分布计算出非视距误差ej的均值和方差为:

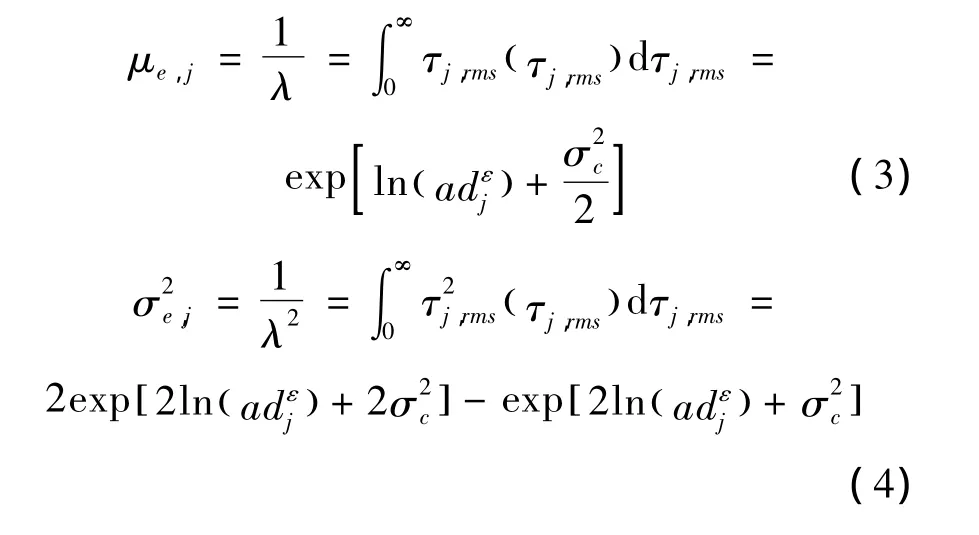
2 TDOA信息的补偿与计算

2.1 TDOA信息的补偿

如前所述，标签与锚节点之间测量的TOA值中可能包含非视距误差量，因此在使用该组TOA所得到的TDOA进行标签定位时，应将该部分误差减去，对TDOA进行补偿。

定义锚节点所在位置为:xi(i=0，1，2，…，N)，标签所在位置为x0(本文只考虑了单个标签的情况)。

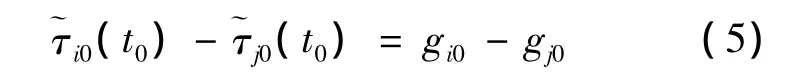
由式(1)与式(5)可推导化简得

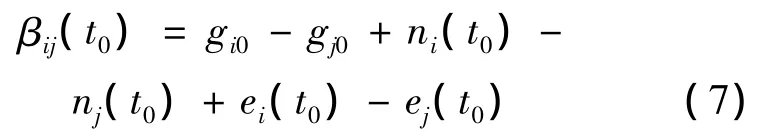
其中:ei(t0)表示锚节点i与标签之间的非视距误差;t0为当前时刻。由式(7)可以看出:影响TDOA信息准确性的主要因素是测量噪声和非视距误差。由式(3)与式(4)可以看出:可通过估计非视距误差信息需求标签与锚节点之间的距离信息来进行计算。因此，首先要使用已有的视距锚节点进行标签位置信息预估，得到的位置信息记为(xk，yk)。使用该预估信息，通过式(3)及式(4)计算对应锚节点的非视距误差信息，并利用该误差信息对存在非视距误差的TDOA信息进行补偿，增加可使用的TDOA信息数目以提升定位精度。补偿过程如下:

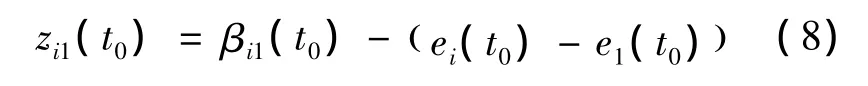
已知共有N个锚节点，则可得到N－1个TDOA方程，联立这N－1个方程组成矩阵型式可得

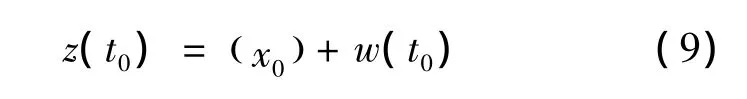
且有:

其中:

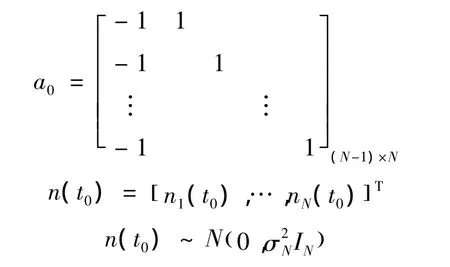
依据前文所提到的理论，系统测量误差与非视距误差是不相关的，因此w的协方差矩阵可以表示为

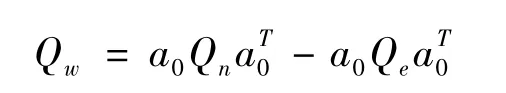
Qe表示多个锚节点的非视距时延均方差联合矩阵，可以表示为

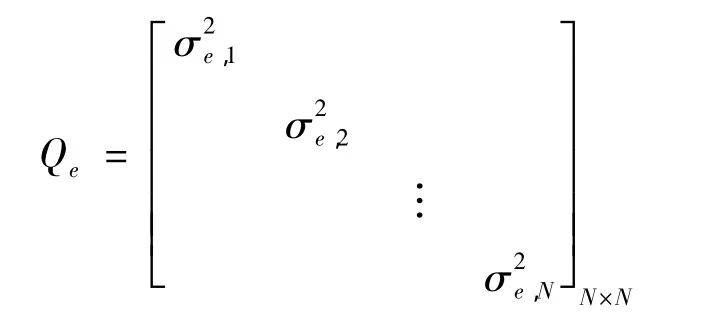
由此可得似然函数为

2.2 标签的定位

通过似然函数可得关于x0的最大似然估计值为

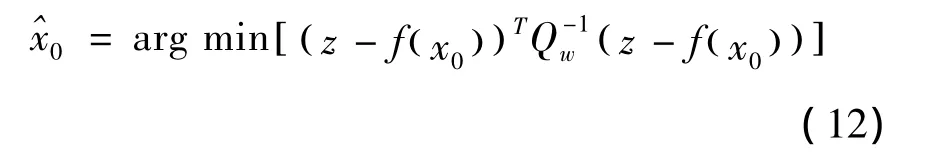
由于f(x0)不是线性函数，因此公式中的估计量不收敛，故需要通过数值极小化来进行求解。以下为一个线性化的过程:

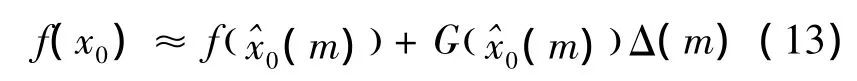
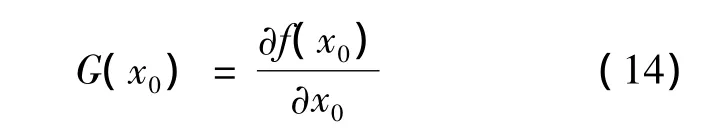
将式(13)代入式(12)以解决线性最小化问题。

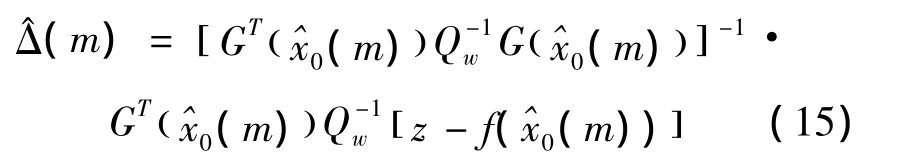
其中:

ri(x0)代表一个单位长度的矢量:

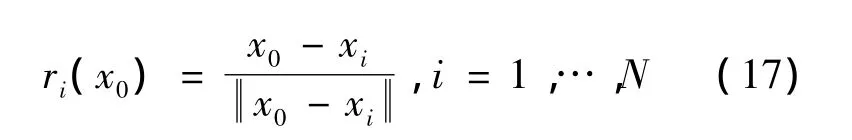
经过m+1次迭代的结果为

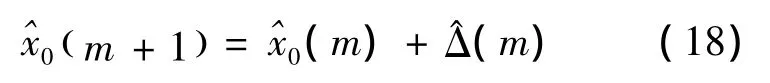
，不断进行迭代。如果迭代前后结果差距大于0.1 mm，则继续迭代过程直到差距小于0.1 mm，此时可确定当前迭代估计结果为所定位标签的位置。

3 仿真性能分析

仿真设定在一个100 m×100 m的二维空间中，存在8个锚节点和1个标签，其位置信息如图2所示。

图2 仿真锚节点位置信息示意图

3.1 TDOA均方差仿真对比

仿真分析了非视距误差均值分别为10－7及10－8时，存在非视距时延的锚节点所计算的TDOA信息均方差、无非视距时延的锚节点所计算的TDOA信息均方差与参考均方差的对比情况(见表1、2，表中数据均为10－9量级)。

表1 非视距误差均值为10－7时的对比情况

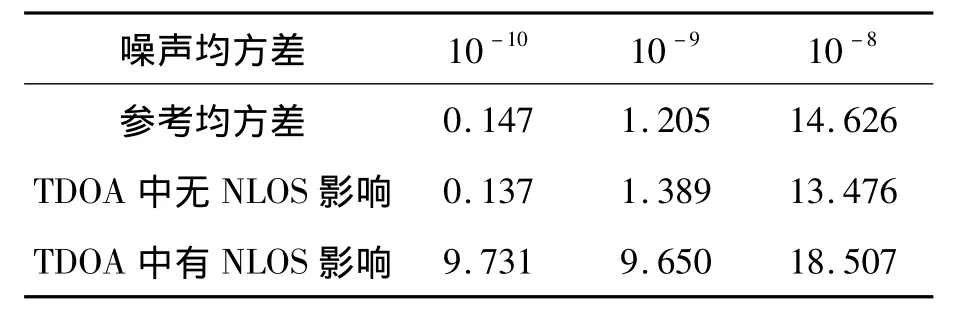
表2 非视距误差均值为10－8时的对比情况

通过仿真结果可以看出:由于非视距时延的存在，使得TDOA信息均方差相对无非视距时延的情况有着较大的改变。当非视距误差均值较大、测量噪声均方差较小时，TDOA均方差相对于参考均方差增大了数倍。即使噪声方差较大时，也能很容易地区分出存在非视距时延的锚节点。该数据表明了改进鉴别算法的有效性，证明了该鉴别算法是可行的。但在非视距误差较小、噪声方差较大时，由于测量噪声掩盖了非视距时延，使得通过均方差不易判断锚节点是否具有非视距。

3.2 不同非视距误差情况仿真分析

仿真分析在相同非视距节点数目、不同非视距误差均值的情况下，改进鉴别补偿算法对定位性能的影响。

图3、4为经过10 000次蒙特卡洛仿真得到的定位误差曲线。图中:“▽”表示无非视距影响情况下的定位误差曲线;“*”表示非视距误差均值为10－7的定位误差曲线;“○”表示非视距误差均值为10－8和10－9的定位误差曲线;纵轴表示定位误差;横轴表示测量噪声均方差;

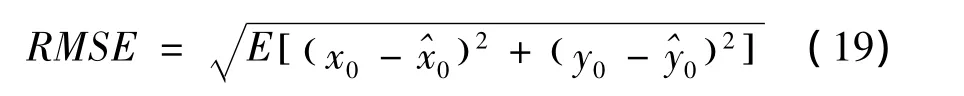
在非视距误差均值为10－7时，非视距误差对于最终定位结果的影响应在30 m左右。但从仿真结果可以看出:通过使用鉴别补偿算法，定位结果曲线与不存在非视距误差的定位结果曲线趋势基本相同，有效地抑制了非视距误差的影响。同时，当非视距误差均值为10－9时，非视距误差对最终定位结果的影响应在0.3 m左右。从仿真结果看出:使用该鉴别补偿算法，同样有效地抑制了非视距误差的影响。仿真结果还表明:当噪声均方差增大时，算法定位精度随之降低。

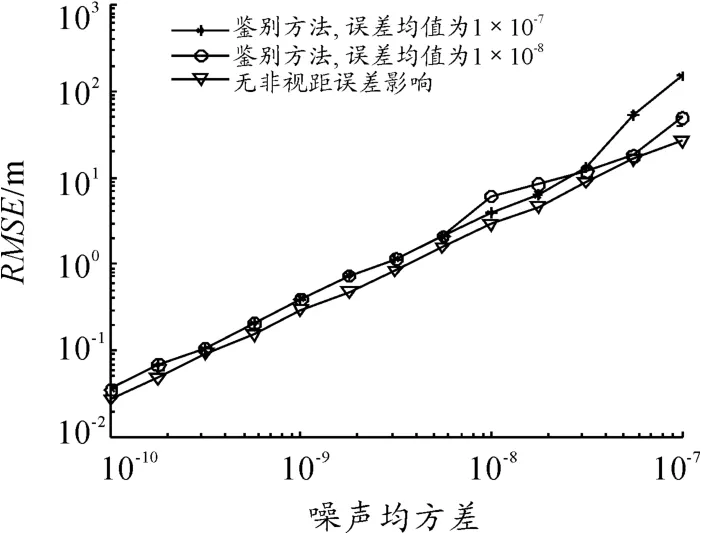
图3 不同非视距误差均值分析图1

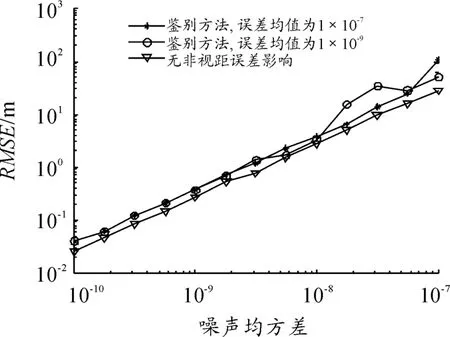
图4 不同非视距误差均值分析图2

3.3 不同非视距节点个数仿真分析

仿真分析不同非视距误差锚节点个数在不同非视距误差均值情况下的定位性能。分别分析了4个锚节点存在非视距误差、一个锚节点存在非视距误差、在非视距误差均值分别为10－7和10－9时的定位误差情况。

图5、6分别为4个锚节点非视距与1个锚节点存在非视距误差，误差均值分别为10－7和10－9时的定位性能对比。图中:“▽”表示无非视距影响情况下的定位误差曲线;“*”表示存在4个具有非视距误差的锚节点的定位误差曲线;“○”表示存在1个具有非视距误差的锚节点的定位误差曲线;纵轴表示定位误差;横轴表示测量噪声均方差。由仿真结果可以看出:改进的非视距误差鉴别补偿算法与无非视距误差的定位误差曲线对比，其趋势基本相同，有效地降低了非视距误差对定位的影响。当非视距节点的个数增多、噪声误差增大时，定位误差也随之增大。

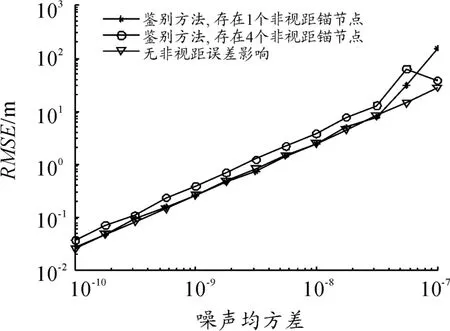
图5 非视距误差均值为10－7时的定位性能对比

图6 非视距误差均值为10－9时的定位性能对比

4 结束语

本文提出了一种非视距误差的鉴别补偿的算法。利用锚节点之间通视的先验条件，计算锚节点之间的TDOA信息均方差作为参考均方差，通过标签与锚节点之间的测量TOA信息计算相应的TDOA信息得到其均方差，将该均方差与参考均方差进行比对剔除非视距锚节点。同时，若定位结果不能满足需求定位精度，可以使用筛选出的视距锚节点预估标签位置，使用非视距时延估计算法估计非视距误差，补偿TDOA信息，从而达到增多可使用的TDOA信息的目的，并以此来提高系统的定位精度。仿真分析结果表明:本文提出的方法成功抑制了非视距误差对定位精度造成的影响，证明了该方法的有效性。

［1］Wu X，Tan S，He Y.Effective error control of iterative localization for wireless sensor networks［J］.International Journal of Electronics and Communications，2013，67(5):397－405.

［2］He Y，Liu Y，Shen X，et al.Noninteractive localization of wireless camera sensors with mobile beacon［J］.IEEE Transactions on Mobile Computing，2013，12(2):333－345.

［3］Huagang Yu，Gaoming Huang，Jun Gao.An Efficient Constrained Weighted Least Squares Algorithm for Moving Source Location Using TDOA and FDOA Measurements［J］.IEEE Transactionson WirelessCommunications，2012.

［4］Zheng Yang，Yunhao Liu.Understanding Node Localizability of Wireless Ad Hoc and Sensor Networks［J］.IEEE Transactions on Mobile Computing，2012.

［5］Yeredor，Arie，Angel，et al.Joint TDOA and FDOA estimation:A conditional bound and its use for optimally weighted localization［J］.IEEE Transactions on Signal Processing，2011.

［6］Lanxin Lin，So H C，Frankie K W，et al.A new constrained weighted least squares algorithm for TDOA-based localization［J］.Signal Processing，2013.

［7］Girod L，Bychovskiy V，Elson J，et al.Locating tiny sensors in time and space:A case study［C］//Werner B，ed.Proc.of the 2002 IEEE Int’1 Conf.on Computer Design:VLSI in Computers and Processors.Freiburg:IEEE Computer Society，2002:214－219.

［8］Patwari N，Ash J N，Kyperountas S，et al.Locating the nodes:cooperative localization in wireless sensor networks［J］.IEEE Signal Processing Magazine，2005，22(4):54－69.

［9］Gustafsson F，Gunnarsson F.Positioning using timedifference of arrival measurements［C］//In Proc.of International Conference on Acoustics，Speech，and Signal Processing(ICASSP).USA:［s.n.］，2003.

［10］李军，张会清.一种室内定位中NLOS误差抑制算法［J］.控制工程，2009，16(7):117－119.

［11］Chan Y T，Ho K C.TDOA-SDOA estimation with moving source and receivers［C］//Proceedings of IEEE International Conference on Acoustics and Signal Processing(ICASSP).USA:［s.n.］，2003.

［12］Torrieri D J.Statistical theory of passive location system［J］.IEEE Trans on Aerospace and Electronic Systems，1984，20(2):183－198.

［13］Chen P C.A non-line-of sight error mitigation algorithm in location estimation［C］//IEEE Wireless Communications and Networking Conference.New Orleans，USA:［s.n.］，1999.

［14］WYLIE M P，HOLTZMAN J.The Non-line of Sight Problem in Mobile Location Estimation［C］//5th IEEE International Conference on Universal Personal Communications.USA:IEEE，1996:827－831.

［15］GREENSTEIN L J.A New Path-gain/delay Spread Propagation Model for Digital Cellular Channel［J］.IEEE Trans.on VT，1997，46(2):177－484.