精密齿轮减速器扭转刚度的精确计算
2015-12-07王光建仝勇军
王光建,仝勇军
(重庆大学机械传动国家重点实验室,重庆 400044)
扭转刚度是精密减速器的一项重要性能指标。传统上扭转刚度的计算通常采用集中参数法[1],忽略了轮齿和轴承的变形,而主要考虑的是轴的变形。在伺服精度和响应要求越来越高的情况下,使用传统计算方法已经不能满足要求。
韩晓娟[2]分别计算了轴与齿轮的扭转刚度,并将两部分串联得出传动系统的刚度,但只是计算了一根轴与一个齿轮的串联刚度,且没有考虑轴承的变形。李建宜[3]计算了一对齿轮的扭转刚度,并进行了有限元仿真,但更多的是计算齿轮啮合刚度。张迎辉等[4]进一步考虑了轮齿廓曲率的影响,避免了单对齿啮合刚度为负的情况,使啮合刚度模型更加精细。Park[5]针对减速器的拓扑结构特点建立了整机扭转刚度半解析模型,但该计算方法较为复杂和繁琐。在啮合刚度计算方面,对齿轮在不同接触位置的啮合刚度,以及多齿接触下变形协调等复杂影响因素的研究也较为全面和深入[6-7]。
本文采用有限元法,综合考虑齿轮轴、轴承和齿轮啮合刚度来精确计算精密齿轮减速器的扭转刚度。
1 精密齿轮减速器系统扭转刚度的集中参数计算
1.1 扭转刚度的计算模型
本文以图1所示的减速器参数为例,齿轮参数如表1所示。根据实际情况电机额定功率P=10 kW,额定转速n=1700 r/min,额定输出转矩为56 N·m。据此对输入端施加转矩T=10 N·m进行计算。
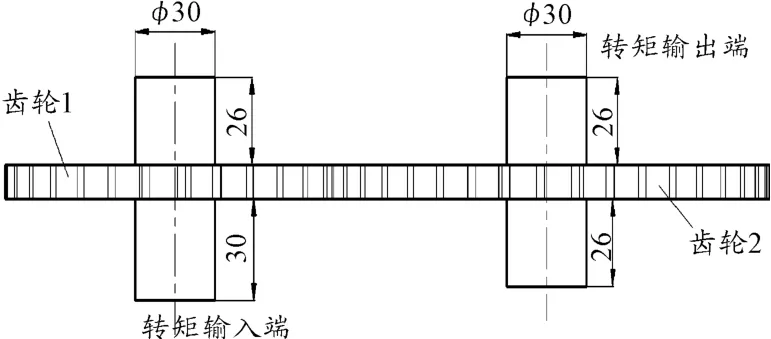
图1 减速器结构
图2中各轴的扭转刚度分别为K1和K4,一对啮合齿轮的扭转刚度分别为K2和K3(轮齿视为具有变截面的悬臂梁),电动机转子的惯量为Jm,负载惯量为JL。将各轴的刚度折算到电机轴上,图2(b)所示系统就进一步被简化为图2(c)所示的单支扭振系统,且轴承对整个系统的扭转刚度没有影响。

表1 齿轮参数
为便于分析计算,首先将图2(a)中的实际传动系统简化为图2(b)中“集中参数”系统。
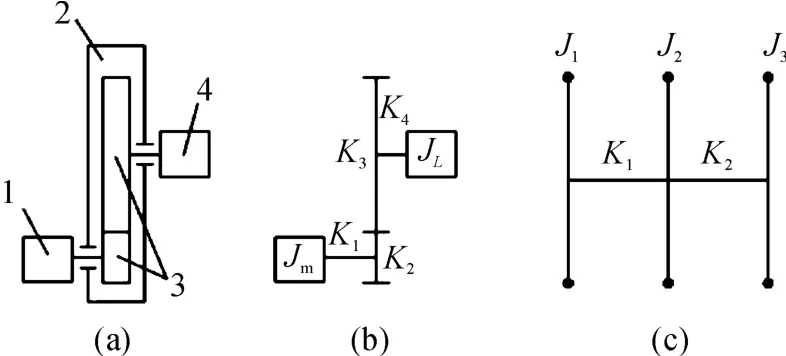
图2 计算模型的建立
1.2 刚度的移轴折算
在减速器扭转刚度的测量方法中,本文选取输出轴锁定,测量输入轴扭矩与产生的扭转角之比的方法。此时需要进行刚度折算。刚度折算是基于折算前后弹性势能不变这一点进行的。如图2所示,如果输出轴刚度为K4,折算到主动轴后的数值为 K4',则
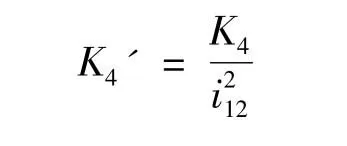
式中,i12为轴1到轴2的传动比。
综上所述,图2(a)所示系统折算之后的扭转总刚度K的计算公式为
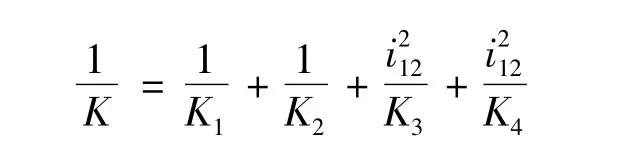
其中:K1为输入轴段刚度;K2为输入齿轮刚度;K3为输出齿轮刚度;K4为输出轴段的刚度。
齿轮传动轴的扭转刚度
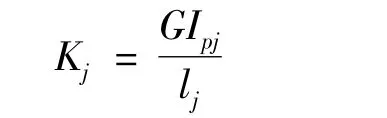
式中:l为轴受扭矩作用的轴长度(mm);GIpj为轴的截面抗扭刚度(MPa·mm4);对于输入、输出轴,j=1,2。
齿轮的刚度由齿轮结构决定。齿轮轮体的刚度远远高于轮齿的刚度,因而可将轮齿视为具有变截面的悬臂梁,一个齿轮的扭转刚度为
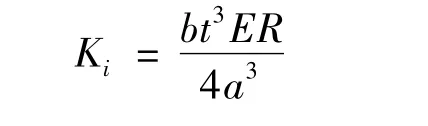
式中:b为齿宽;t为齿厚;E为齿轮材料的弹性模量;R为齿轮节圆半径;a为齿高。
1.3 不考虑齿轮啮合刚度的集中参数法计算
在不考虑齿轮变形的情况下,精密减速器的扭转刚度K的计算公式为
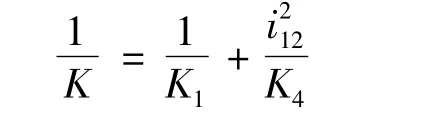
即K=6.12×104N·m/rad,输入轴转过的角度为1.64 ×10-4rad。
1.4 考虑齿轮啮合刚度的集中参数法计算
在考虑了齿轮变形情况下,精密减速器的扭转刚度K=5.84×104N·m/rad,输入轴转过的角度为1.71 ×10-4rad。
2 精密减速器扭转刚度有限元计算
2.1 不考虑轴承变形时的扭转刚度有限元计算
2.1.1 有限元模型的建立
对于一般的圆柱直齿轮传动,其在一个啮合周期中的单齿啮合区和双齿啮合区(直齿轮重合度小于2时只有这两种)扭转刚度不同,但是对于整个减速器的扭转刚度而言,这种变化影响不大的,所以本文齿轮均选取单齿。
根据以上参数在Pro/E中建立三维模型,然后导入到HyperMesh中,采用映射方式划分六面体单元,单元类型选择SOLID185单元,材料类型弹性模量 E=2.07 ×1011Pa,密度 ρ=7830 kg/m3,再导入到ANSYS进行计算。有限元模型如图3所示,共计357058个单元,372821个节点。

图3 不考虑轴承变形的有限元模型
2.1.2 边界条件设置及加载
由于没有考虑轴承的影响,对输出轴的转矩输出端面全约束,其余轴的端面约束径向和轴向位移以模拟轴承的作用。
选择输入轴的单元在柱坐标下的切向线位移,如图4所示。
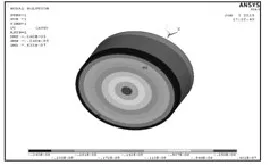
图4 输入轴的切向线位移
由图4可知:输入轴最大线位移为2.6×10-6m,输入端面转过的角度均为1.73 ×10-4rad,比本文采用集中参数法(1.3节)计算的值大5.5%,比本文1.4节计算的值大1.2%。
2.2 考虑轴承变形时的扭转刚度有限元计算
在考虑轴承(深沟球轴承6206)情况下整个模型划分的六面体网格如图5所示,共计613754个单元,620559个节点。轴承钢球与滚道之间建立接触,轴承内孔与轴之间建立接触。轴承外圈全约束,输出轴端全约束,输入轴端不约束,约束2个轴其余2个面的轴向位移,先施加扭矩T=10 N·m。
输入轴单元在柱坐标下的切向线位移如图6所示。由图6可知:输入端面的线位移大小是不同的,原因是输入轴在齿轮啮合力作用下会变形,从而导致输入端面的位移由两部分组成:一部分是在齿轮啮合力作用下产生的;一部分是由所施加扭矩产生的。输入端面在直角坐标下的X方向与Y方向的位移如图7所示。

图5 考虑轴承变形的有限元模型
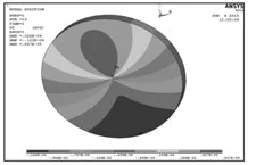
图6 输入端面的切向线位移
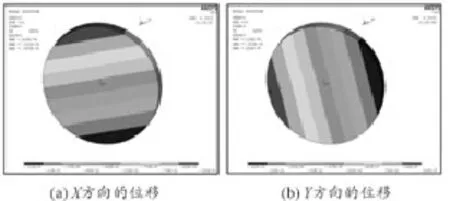
图7 输入端面在直角坐标下的位移
把输入轴端圆心和端面最外圈一周节点的X方向与Y方向位移数值导入到Matlab中进行处理,可得输入端所有节点转过角度是一样的,均为2.1 ×10-4rad。
再分别计算输入转矩 T=20,30,40,50 N·m的情况。有限元计算得到的扭转变形与集中参数法得到的结果的对比如图8所示。
从图8可知:采用集中参数法计算得到减速器扭转变形在不同输入扭矩作用下是线性的,但是当整个模型考虑轴承变形时,减速器刚度在不同输入扭矩作用下是非线性的,这也更接近实际情况。
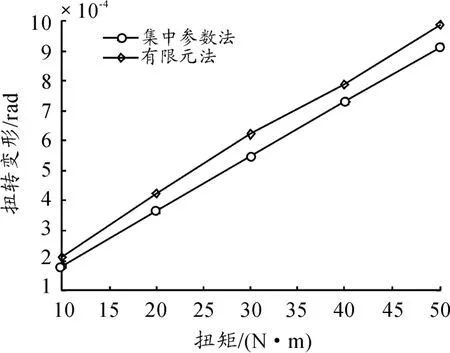
图8 齿轮减速器扭转变形对比曲线
综上可以得到采用不同方法计算的精密减速器固有频率对比如表2所示。

表2 不同计算方法结果的对比
由表2可知:传统的集中参数法不考虑齿轮变形得到的减速器扭转刚度比考虑轴承的有限元法大19.7%,而考虑齿轮变形得到的减速器扭转刚度比考虑轴承的有限元法大15%。因此,本文1.4节计算的减速器扭转刚度更准确,考虑轴承的有限元计算结果更接近实际情况。
3 在轴承等效情况下对精密减速器扭转刚度的有限元计算
由于上述模型的网格数量太多,计算时间太长,为减少计算时间,考虑用套筒来等效整个轴承。仍然加载转矩T=10 N·m。齿轮啮合的法向载荷 Fn=177.36 N,根据赫兹接触理论[8]计算得到6206深沟球轴承在Fn的作用下的最大位移为0.0044 mm,由此套筒的弹性模量为734.8 MPa,其他部分弹性模量仍为2.1×1011Pa。整个模型共划分为466947个单元,475638个节点,见图9。
输入轴端在直角坐标下的位移如图10所示。输出轴端圆心和端面最外圈一周的X方向与Y方向位移导入到Matlab中处理后得到外圈所有节点所转过的角度是一样的,均为 2.083×10-4rad。用此方法计算的精密减速器刚度为4.8×104N·m/rad。
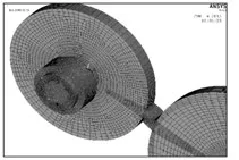
图9 套筒等效的有限元模型

图10 直角坐标下的位移
再分别计算输入转矩 T=20,30,40,50 N·m的情况。有限元计算得到的扭转变形曲线与集中参数法计算得到的结果的对比如图11所示。
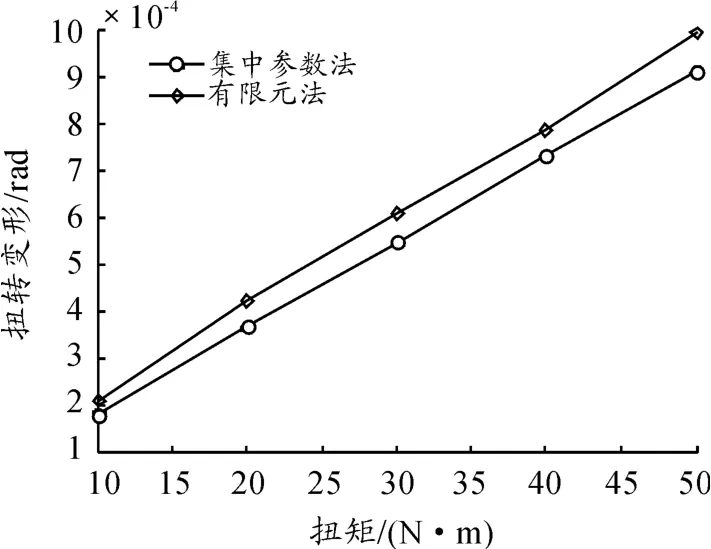
图11 套筒等效情况下的扭转变形曲线
由图11可知:套筒等效情况下计算得到的减速器刚度曲线也是非线性的,而且与直接用轴承计算的情况有较好的一致性。说明这种等效方法真实可信,为精密减速器的扭转刚度计算提供了一种快速有效的方法。
4 结论
考虑轴、轴承的变形和齿轮的啮合刚度,分别采用集中参数法和有限元法来计算精密齿轮减速器的扭转刚度,分析了不同计算方法的误差。
1)由于考虑了轮齿变形和轴承变形,因此有限元法计算的精密减速器扭转刚度偏低,固有频率偏低;与有限元方法(考虑轮齿和轴承变形)相比,集中参数法计算(不考虑轴承和轮齿变形)的扭转刚度增加了28%。
2)为了减小计算时间,提高计算效率,采用套筒等效刚度代替轴承刚度进行有限元计算,其结果与代替前的计算结果基本一致,比代替前增加了0.3%。
3)虽然轴承变形计算为非线性接触计算,但扭转变形结果与集中参数法计算结果基本一致。
[1]孙麟治,张鄂,赵明晶,等.小模数精密齿轮传动设计[M].北京:机械工业出版社,1985.
[2]韩晓娟.齿轮传动系统刚度的确定方法[J].力学与实践,1998,20(4):66-67.
[3]李建宜.齿轮扭转啮合刚度研究[D].太原:太原理工大学,2006.
[4]张迎辉,肖君君,何卫东.机器人用 RV减速器针摆传动啮合刚度计算[J].大连交通大学学报,2010,31(2):20-23.
[5]Park J S.Stiffness and error analysis of the cycloid drive[D].Korea:College of Engineering,Seoul National University,2006.
[6]LIU Jingya,MATSUMURA Shigeki,CHEN Bingkui,et al.Torsional Stiffness calculation of double-enveloping cycloid drive[J].Journal of Advanced Mechanical Design,2012,6(1):2-14.
[7]Zhang Xiuyan,Dai Xiaojun.Meshing stiffness analysis of four ring-plate-type pin-cycloid gear planetary drive[J].Applied Mechanics and Materials,2012,229-231:499-502.
[8]冈本纯三.球轴承的设计计算[M].黄志强,译.北京:机械工业出版社,2003.
