基于谱元法的加筋双层板声透射分析
2015-12-05李兰清
李兰清,郑 辉,2
(1.上海交通大学 上海市复杂薄板结构数字化制造重点实验室,上海 200240;2.上海交通大学 振动、冲击、噪声研究所,上海 200240)
基于谱元法的加筋双层板声透射分析
李兰清1,郑 辉1,2
(1.上海交通大学 上海市复杂薄板结构数字化制造重点实验室,上海 200240;2.上海交通大学 振动、冲击、噪声研究所,上海 200240)
首先应用谱元法(SEM)建立简支加筋双层板结构在简谐平面声波激励下的振动响应分析模型,将所得结果与有限元法(FEM)计算结果对比,表明谱元法(SEM)在求解该类问题时具有精度高和求解速度快的优点。然后应用Rayleigh积分求解加筋双层板结构路径传声的透射声功率。在筋板截面面积不变的约束条件下,研究筋板倾角与面板间距在声波正入射情况下对透射侧面板辐射声功率的影响。结果表明:筋板倾角越大,加筋双层板的透射声功率越小;在倾角小于22º的情况下,隔声性能随着面板间距的减小而提高。分析结果对加筋双层板的结构设计与隔声优化具有一定的指导意义。
声学;加筋双层板;声透射;谱元法;振动—声学响应;辐射声功率
加筋双层板具有质量轻、刚度大、良好的抗冲击性能等优点,在诸如汽车、航天、航空和航海等领域有着广泛应用。同时,由于结构的特殊性,在声学领域,也常被用作隔声材料,尤其对载运工具高速行驶时的空气动力噪声起到隔声作用。
声透射损失作为加筋双层板的振动-声学性能指标之一,和诸如比强度和比刚度等力学性能指标一样吸引了许多学者开展大量的理论和实验研究。辛锋先等人对这一领域已开展的研究工作进行了较为全面的综述[1]。在理论研究方面,大多数解析模型对筋板进行了简化,如简化成刚性体或平移/转动弹簧等[2]。近期分析夹层板声辐射问题相对完备的理论模型是Xin和Lu[3]的模型。他们的理论模型不仅考虑了筋板质量的惯性影响,并在振动控制方程中增加了筋板扭转力矩引起的惯性项。在实验研究方面,王巧燕和葛剑敏[4]用混响室—混响室法针对高速机车车体用波纹夹层板的隔声性能进行系统测量,分析了双层铝合金加筋板的面板厚度、面板间距等各项参数对其隔声性能的影响。除了理论与试验研究,数值仿真方法由于不受几何复杂性的限制也被用于求解结构的振动响应。如有限元法(FEM)和边界元法(BEM)或者它们的组合被广泛应用于求解夹层板结构的振声学响应。王义柏等人就曾用FEM研究单向加筋双层板的隔声性能[5]。但用FEM计算结构的振声学响应时,随着频率的增大,要不断细化网格尺寸,以保证求解精度。Alford等人曾提出网格尺寸最好小于1/10~1/20的最高频率所对应的波长[6]。根据Alford等人提出的网格划分准则,有限元法在求解高频问题时存在网格数量多、内存需求大、耗时长等缺点,尤其在求解二维、三维问题时更为突出。
相较于有限元法的刚度矩阵与频率无关,谱元法(SEM)采用基于波动解推导的插值函数,该插值函数与频率相关且波动解在频域内精确满足运动方程,因此SEM可以提供更加精确的频域解[7]。谱单元法理论是上世纪80年代由Patera提出,早期主要用于计算流体动力学[8]。后来Seriani等人[9,10]将谱元法用于声学问题和弹性波传播问题。他们提出的一维和二维矩形单元用于均匀介质中的声波和弹性波传播分析,显示了该方法的优点:即使在中频域也能得到满意的声波传播计算结果。Birgersson等人[11]基于SEM针对单层板结构建立了高频分布随机载荷激励下的振动响应模型。Ei-Raheb[12]用谱元法(SEM)研究了夹层梁的声透射问题。
本文首先应用SEM推导杆的纵向振动与欧拉-伯努利梁横向振动的谱元公式[13]。然后在不考虑加筋双层板与声腔介质耦合的前提下,基于谱元法(SEM)建立了加筋双层板结构传递路径(Structure borne transmission path)的振动响应模型。利用杆—梁谱单元的组合来求解加筋双层板结构在简谐平面波激励下的振动响应,所得结果与有限元计算结果比较,验证谱元法的可靠性与优越性。随后应用Rayleigh积分计算透射侧在激励频带内的平均声功率,在筋板截面面积不变的约束条件下,研究筋板倾角与面板间距等元素在声波正入射条件下对加筋双层板声透射的影响。
1 杆与梁的谱元公式
1.1 纵向振动杆的谱元公式
纵向振动的均质杆控制方程为
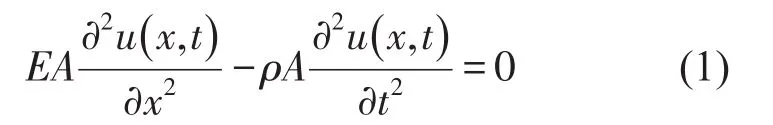
式中E、A、ρ、u(x、t)分别表示杆的弹性模量、横截面积、密度和纵向位移。轴向内力为
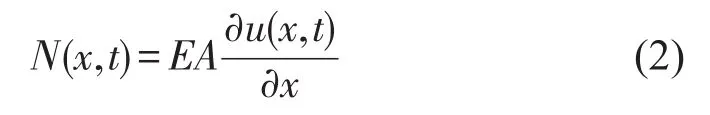
对位移u(x,t)进行Fourier分解,可得
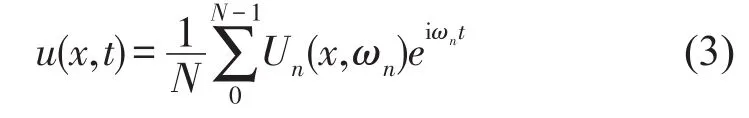
其中Un(x,ωn)是位移u(x,t)的谱分量,将式(3)代入式(1)并忽略下标n,可得到式(1)的通解
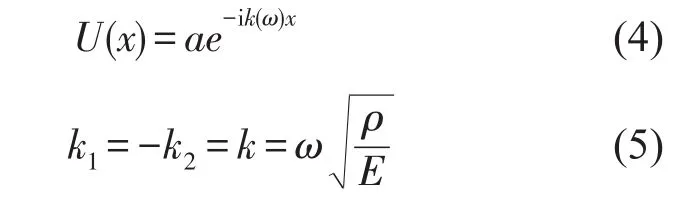
设长为L的轴向振动杆的结点位移向量为
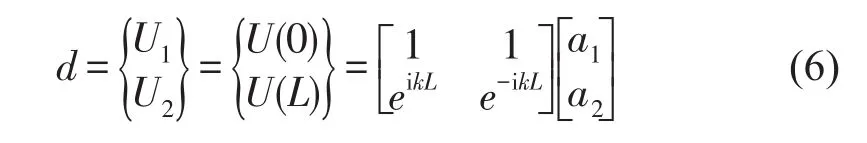
结点的轴向力为f=[N1N2]T,根据式(2)、式(5)与式(6)可以得到结点的位移—力的关系,其中S(ω)为与频率相关的刚度矩阵。
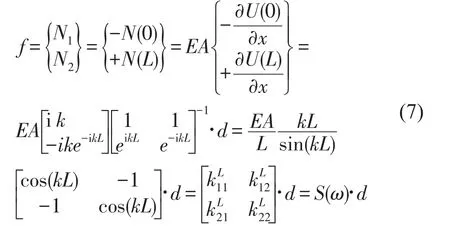
1.2 Euler-Bernoulli梁的谱元公式
Euler-Bernoulli梁横向振动的控制方程为
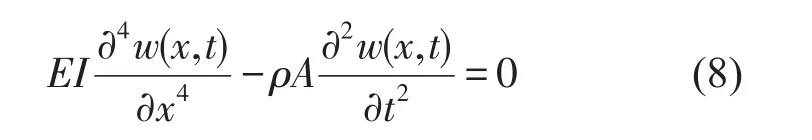
剪切内力Q(x,t)、弯矩M(x,t)与横向位移w(x,t)的关系如下
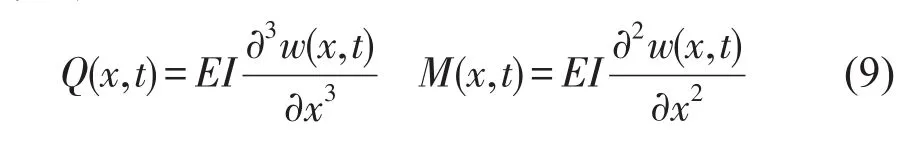
与杆的谱元公式类似,将梁的横向位移w(x,t)写成如下形式
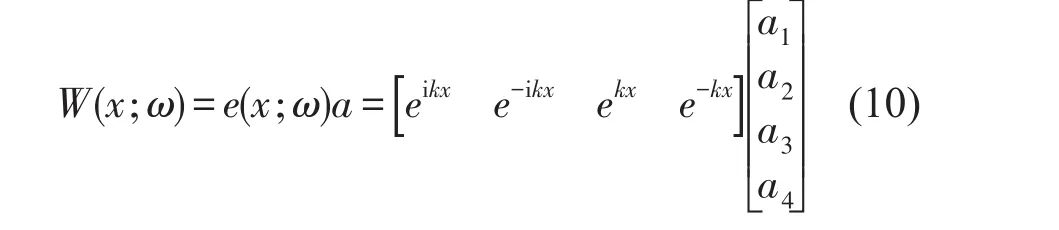

根据式(9)、式(10)与式(11),可得结点力与位移的关系为

1.3 杆—梁组合系统的谱元公式
为了满足相邻单元在边界上位移与力的连续性,将式(7)与式(12)加以整合,可以得到局部坐标系下谱单元结点力与结点位移的关系为
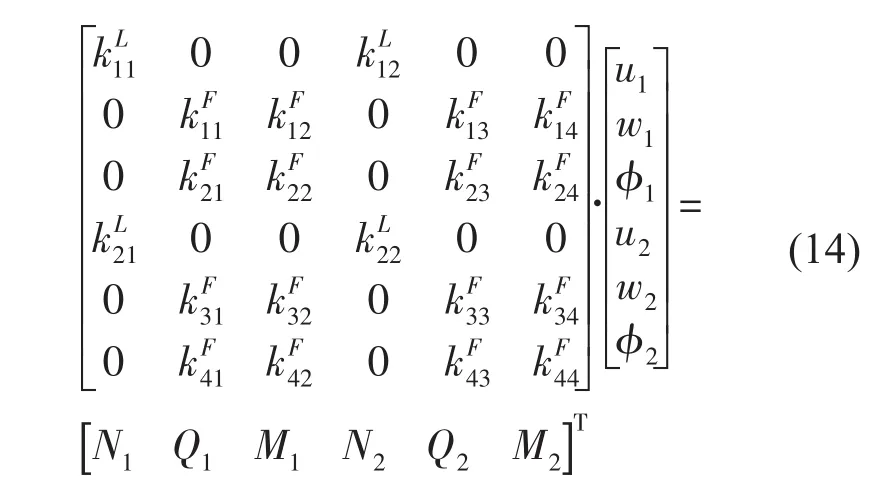
为了求解整体结构的动力学特性,需将局部坐标下的谱单元刚度矩阵与所受外力矩阵变成整体坐标。按照一定的关系组合,可以得到整个系统结点力与结点位移的关系为

式中S(ω)为整体坐标下的结构刚度矩阵,与频率有关。通过求解式(15),即可求出整个系统的振动响应。
2 谱元法求解加筋双层板在声波激励下的振动响应
本文将只考虑结构路径传声的加筋双层板看作是一个杆梁组合系统,应用谱元法来求解该杆梁系统在简谐平面波激励下的振动响应。加筋双层板的结构模型如图1所示。
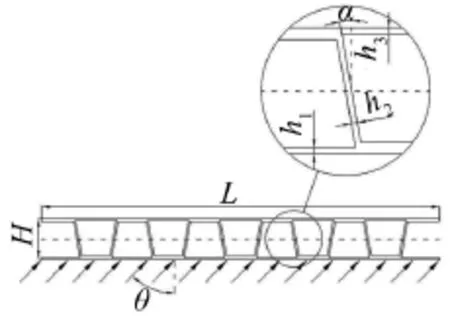
图1 梯形加筋双层板模型
该组合系统的梁可以分为三类:
①下梁:下层梁受到斜入射角度为θ的声激励作用,厚度为h1,长度为L;
②筋梁:中间筋板梁连接上下两层梁,厚度为h2,共有N根筋,筋板与竖直方向倾角为α,N根筋与两面板的中心平等线相交于垂直线的中点;
③上梁:上层梁对外辐射声压,厚度为h3,与下层梁的间距为H。
如图1所示,结构的几何参数为:L=1 m,H=0.1 m,h1=h2=h3=0.005 m,α=10º,筋的数量N=10。结构材料参数为:杨氏模量E=7.1×1010Pa,泊松比v=0.33,密度 ρ=2 700 kg/m3,阻尼系数η=0.1。声波压力 f(x)=,其中kx=ω/c0×sinθ,P0=1。
分别使用有限元法和谱元法计算该结构在简谐平面波斜入射角度θ=30º情况下的振动响应。为简单起见,对上面板的振动能量进行比较。振动能量的表达式为
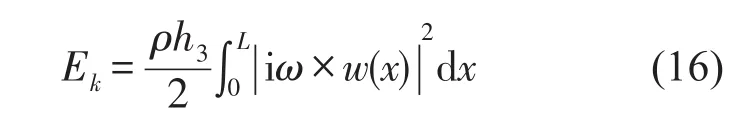
所得到的上面板横向振动能量随激励频率的变化关系如图2所示。
由图2对比可以看出,谱元法计算加筋双层板的振动响应与有限元法相比,振动能量和结构的共振频率都可以很好地吻合。由此证明了方法的正确性与有效性。值得指出的是,计算该结构在645个频率点的振动响应,有限元法共耗时5 074 s,而SEM方法求解耗时122 s,SEM的计算时间仅为有限元计算的3%。可见SEM用于求解双层加筋板这类结构振动响应问题的计算效率远远高于FEM。并且,对于参数分析,SEM可以快速地变化结构参数进行重新计算,而FEM模型需要重新建模或者更新网格才能计算,因而SEM应用于结构-声学优化具有极大的优势。
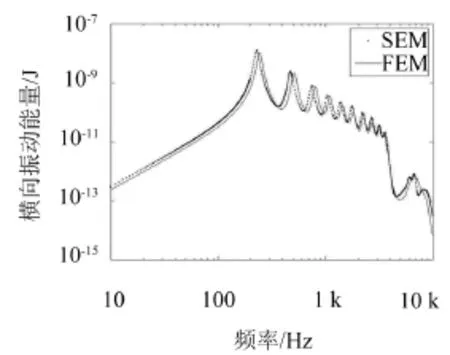
图2 梯形加筋板上面板的横向振动能量对比
3 筋板倾角与面板间距对梯形加筋板隔声性能的影响
加筋双层板的隔声性能可以由透射侧面板的辐射声功率看出,若透射声功率越小,说明从下面板传递到上面板的声能量越小,即结构的隔声性能越好。由式(15)可以求得加筋双层板上面板的横向振动响应,再由Rayleigh积分[14]求得上面板在极坐标中点(r,φ)处的辐射声压p(r,φ;f)为

上面板的辐射声功率可以表示为
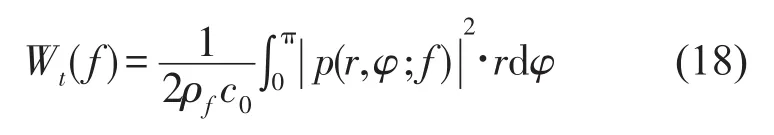
在筋板截面面积不变的约束条件下,通过改变筋板的结构参数,研究筋板倾角与面板间距等几何参数在声波正入射条件下对隔声性能的影响,为加筋板振声学特性分析和声学设计提供数据支持。
为了确保筋板的截面面积不变,首先要研究面板间距H与筋板倾角α对筋板厚度h2的影响。以筋板参数为H=0.1 m,h2=0.05 m,α=0º的筋板面积S作为参照,考察面板间距在50 mm~150 mm范围内(取值间隔为5 mm),筋板倾角在0~30º范围内(取值间隔为1º)共651个不同的梯形加筋双层板谱元模型在声波正入射条件下的平均声辐射功率。不同面板间距与筋板倾角情况下的筋板厚度由下式求出。
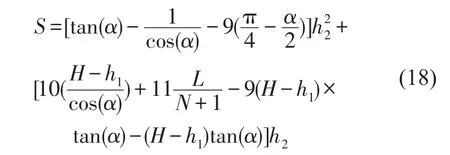
式中不变的几何参数为:L=1 m,N=10,h1=h3=0.05 m;材料参数与上文的相同。以10 Hz~1 000 Hz为考察频带,以上面板的平均透射声功率Wtm为考察对象。频率区间为f1~f2的平均辐射声功率Wtm的表达式为

计算得到的透射声功率的频带均值Wtm随面板间距和筋板倾角的变化规律如图3所示。

图3 透射声功率的频带均值Wtm随筋板倾角和面板间距的变化规律
由图3所示结果可以看出,筋板的倾角对结构的隔声性能影响与面板间距有关。总的趋势是,随着筋板倾角的逐渐增大,透射的声功率越小。即随着筋板倾角的增大,梯形加筋双层板结构的隔声性能越好。这是由于在筋板截面面积与面板间距不变的约束下,随着筋板倾角的增大,斜筋的长度越大,筋板的声桥作用减弱。这也说明相同质量面密度条件下,梯形加筋双层板的隔声性能优于矩形加筋双层板。
此外,在筋板斜筋倾角为0~22º范围内,面板间距越大,上面板的辐射声功率越大。即在此范围内,梯形加筋板的隔声性能随着面板间距的增大而减小。这是由于在固定筋板截面面积与倾角的情况下,面板间距越大,斜筋的长度在变长,筋板的厚度减小。此时筋板连接上下面板的声桥作用在增强,透射到上面板的声能量变大,隔声变差。在筋板倾角为22º~30º之间,加筋板的隔声性能随面板间距体现出无规则的变化规律。
4 结语
谱元法用于计算加筋双层板在声激励下的振动响应,在保证相同计算精度条件下,计算效率远远高于有限元法。此外,谱元法还可以快速地变化结构参数进行重新计算,而有限元法模型需要重新建模或者更新网格才能计算。因而谱元法应用于加筋双层板的结构—声学优化具有极大的优势。
加筋双层板的筋板倾角与面板间距对结构的隔声性能有显著影响。在筋板截面面积不变的约束下,筋板倾角大的加筋双层板的隔声性能越好;在倾角小于22°的情况下,隔声性能随着面板间距的减小而增大。这些结果可以为梯形加筋板振—声学特性研究和优化设计提供一定的数据支持。
[1]辛锋先,张钱城,卢天健.轻质夹层材料的制备和振动声学性能[J].力学进展.2010,40(4):375-399.
[2]J Wang,T J Lu,J Woodhouse,et al.Sound transmission through lightweight double-leaf partitions:Theoretical modeling[J].Journal of Sound and Vibration,2005, 286:817-847.
[3]F.X.Xin,T.J.Lu.Analytical modeling of wave propagation in orthogonally rib-stiffened sandwich structures:Sound radiation[J].Computers and Structure, 2011,89:507-516.
[4]王巧燕,葛健敏.双层铝合金加筋板隔声性能的实验研究[J].声学技术,2009,28(5):207-208.
[5]王义柏,魏智平,郑辉.单向加筋双层板隔声性能的有限元分析[J].噪声与振动控制,2014,34(4):96-100.
[6]F Fahy,J Walker.Advanced Applications in Acoustics[M]. Noise and Vibration,London,Spon Press,2004.
[7]R J Banerjee.Dynamic stiffness formulation for structural elements: a general approach[J]. Computers & Structures.1997,63(1):101-103.
[8]A T Patera.A spectral finite element method for fluid dynamics:Laminarflow in achannelexpansion[J]. Journal of Computational Physics,1984,54:468-488.
[9]E Priolo,G Seriani.A numericalinvestigation of Chebyshev spectral element method for acoustic wave propagation[C].Proceedings of 13thIMACS Conference(Edited by R.Vichnevetsky),Dublin,1991,551-556.
[10]E Priolo,G Seriani.Spectral element method with substructuring:an accurate and efficient high-order finite element approach to wave Modeling[C].Environmental Acoustics:International Conference on Theoretical and Computational Acoustics-Volume II(Edited by D.Lee& M.H.Schultz),Singapore,1994:509-527.
[11]F.Birgersson,S.Finnveden,C.M.Niosson.A spectral super element for modeling of plate vibration.Part Ι: general theory[J].Journal of Sound and Vibration. 2005,287:297-314.
[12]M Ruzzene.Vibration and sound radiation of sandwich beams with honeycomb truss core[J].Journal of Sound and Vibration,2004,277:741-763.
[13]Usik Lee.Spectral element methods in structural dynamics [M].Singapore,John Wiley&Sons(Asia)Pte Ltd,2009: 42-53.
[14]A Akay,L Michael.Sound radiation from an impactexcited clamped circular plate in an infinite baffle[J]. Journal of the Acoustic Society of America,1983,vol. 72:640-648.
(简讯)
PCB压电传感器技术(北京)有限公司

适合次声波测量的新型½"低频传声器,低于人类正常听力范围的低频范围。
PCB®最新研发的1/2"传声器及前置放大器系统378A07,针对低频测试,适用于研究风力发电机或者例如龙卷风等自然现象。
PCB®1/2"自由场预极化传声器和前置放大器系统378A07。
低频测量在风力发电机、音爆、柴油发动机和专业扬声器系统中广泛使用。378A07传声器可以探测出这些具有潜在危险的低频信号。这款自由场预极化传声器的频响范围为0.13 Hz~20 kHz(+/-2dB),符合IEC 61094-4测量测试传声器标准。这涵盖了低于人类正常听力范围的次声波。378A07传声器通过了A2LA和ILAC的认证,和PCB®公司的其他产品一样,它具有“100%客户满意”保证。
更多信息,请访问www.pcb.com/acoustics或联系声学产品经理胡爱军先生:jhu@pcb.com。
Sound TransmissionAnalysis of Sandwich Plates Based on Spectral Element Method
LI Lan-qing1,ZHENG Hui1,2
(1.Shanghai Key Lab for Digital Manufacture of Complex Thin-walled Structures, Shanghai Jiaotong University,Shanghai 200240,China; 2.Institute of Vibration,Shock&Noise,Shanghai Jiaotong University,Shanghai 200240,China)
A theoretical study on the vibration response of sandwich plates with typical corrugated cores under incident plane sound wave excitation was done by using spectral element method(SEM).Accuracy and efficiency of the SEM were validated by comparing the results with those of FEM.The transmission sound power through the sandwich plates under the normal incidence of the plane sound wave was calculated by applying Rayleigh integral.The effects of the distance between the two faceplates and the inclination angle of the stiffening core on the transmission acoustic power were studied under the condition of constant cross sectional area of the whole structure.It is shown that the transmission sound power of the reinforced sandwich plate decreases as the inclination angle of the corrugated core increases.When the inclination angle of the core is less than 22o,the transmission sound power reduces with the decrease of the distance between the two faceplates. These results are meaningful to the structural design and vibro-acoustic optimization of sandwich plates with corrugated cores.
acoustics;sandwich plates;sound transmission;spectral element method;vibro-acoustic performance; acoustic radiation power
TB532;TH113.1
A
10.3969/j.issn.1006-1335.2015.03.039
1006-1355(2015)03-0181-05
2014-09-29
国家自然科学基金面上项目(NSFC 51275285)
李兰清(1989-),女,硕士研究生,目前从事噪声、振动控制领域的研究。E-mail:lilanqing09@sjtu.edu.cn
郑辉,男,教授,博士生导师。E-mail:huizheng@sjtu.edu.cn
