硬岩掘进机的动力吸振方案优化研究
2015-12-05邹晓阳
李 献,邹晓阳,徐 海,郑 辉,
(1.上海交通大学 振动、冲击、噪声研究所,上海 200240;2.上海交通大学 上海市复杂薄板结构数字化制造重点实验室,上海 200240;3.中铁十八局集团有限公司,西安 710400)
硬岩掘进机的动力吸振方案优化研究
李 献1,邹晓阳2,徐 海3,郑 辉1,2
(1.上海交通大学 振动、冲击、噪声研究所,上海 200240;2.上海交通大学 上海市复杂薄板结构数字化制造重点实验室,上海 200240;3.中铁十八局集团有限公司,西安 710400)
针对某隧道掘进工程中硬岩掘进机(TBM)的振动进行了实地测量。通过现场测试的结果可以看出,TBM推进系统在整个工作过程中振动剧烈,且主梁振动加速度响应在15Hz附近处出现明显的峰值。为降低TBM推进系统的振动水平,提出利用动力吸振器对TBM系统的振动进行抑制的方案。传统动力吸振器必须要有足够的附加质量才能达到良好的吸振效果,然而,TBM系统质量巨大且安装空间有限,吸振器的附加质量很难做到足够大。为此提出应用杠杆机构来实现放大吸振器的附加质量的方案,并设计了适用于TBM推进系统的动力吸振器。通过TBM整机—动力吸振器动力学建模分析,得到系统的频率响应函数,进而利用定点理论求得吸振器的最优同调条件与最优阻尼条件,最后对比传统动力吸振器和质量放大吸振器对主系统的抑振效果。结果表明,优化后的质量放大吸振器在吸振效果上较传统动力吸振器具有明显的优势。
振动与波;硬岩掘进机;动力吸振器;杠杆原理;质量放大;定点理论
硬岩掘进装备(TBM)是铁路、公路、水利、市政建设等隧道施工的重大装备[1]。其破岩效率和推进速度备受关注。但TBM在掘进工作时振动剧烈,使得其内部关键部件由于动应力过大而损坏,由此造成零部件更换和停机事故,直接影响施工进度[2-4]。另一方面,振动幅度过大使得TBM导向误差增大和控制难度增加,影响施工精度。由主机架、主梁、推进缸、撑靴等在内的部件组成推进系统,是TBM主机的骨架。TBM实地掘进时,在滚刀处受到强激励,并通过刀盘、主轴承、主驱动和主梁等传递至撑靴,引起推进系统的整机振动;同时,复杂的整机振动又会对包括推进系统在内的液压设备带来严重的影响[5]。
本文对某隧道掘进工程中所使用的TBM的振动情况进行了现场测量。该隧道掘进工程的现场地质组成主要为Ⅲ、Ⅳ类围岩,岩石硬度偏中软。主隧洞主要利用敞开式TBM进行开挖。敞开式TBM通过撑靴支撑在洞壁形成顶推点,进而由推进油缸推动主梁和主机向前实现掘进,TBM推进系统所施加的推进力在滚刀破岩中起主导作用[6]。根据现场实地测量结果,TBM掘进系统在工作工程中在某一特定频率处具有明显的振动峰值。为此,本文采用对在某一窄带频率范围内的振动具有良好抑制效果的被动动力吸振器作为TBM系统的抑振措施。
传统被动吸振器的吸振效果与吸振器的附加质量关系密切,附加质量越大,则吸振效果越好。在实际工程中,往往受限于安装空间及对总质量的控制,使得吸振器的附加质量受到严格限制。杠杆装置可以有效的对系统的惯性力、弹性力及阻尼力起到放大效果。顾明等人通过利用杠杆装置对弹性力的放大作用,显著地减小悬置吸振器的静变形,降低了弹簧非线性对系统的影响[7],并将半主动型杠杆式吸振器应用于大跨度桥梁风致振动的抑制中[8]。Li[9]对杠杆式吸振器的性能评价做了系统的研究,并对弹性力和阻尼力的放大效果做了定性分析。背户一登等人将定点理论应用于单摆式制振装置,通过杠杆机构使惯性力和阻尼力得到放大,并将该装置应用于建筑抑振当中[10]。
根据TBM的质量大且安装空间有限的特点,本文利用杠杆原理,设计了一种新型的应用于TBM系统的具有质量放大效果的动力吸振器,并对其刚度与阻尼参数进行了优化,从而通过较小的附加质量来达到较为理想的抑振效果。
1 现场测试与结果分析
1.1 测试现场
振动测试系统的振动响应信号传感采用ICP集成压电式三向加速度传感器。传感器信号通过单芯屏蔽线传输至动态信号采集系统记录储存,所采用的动态信号采集系统为坚固型动态信号记录仪(16通道,可扩展),该记录仪的同步采用频率为100 kHz/通道,记录信号采集的各个状态和信号可同步回放。安装有控制分析软件的笔记本电脑用于动态信号记录仪记录信号的时域、幅值域和基于FFT的频域分析软件,实现各测点测得的振动加速度信号的幅值谱和功率谱密度的分析及二次后处理及输出分析结果。
振动测试中,主要的测点布置如图1所示。主梁下部、撑靴、推进缸两端体、支撑缸缸体上各有一个测点。

图1 TBM推进系统测量传感器布点
1.2 测试结果与分析
主梁下测点及其三向加速度传感器方向如图2所示,加速度传感器方向为X轴水平向左,Y轴水平向前,Z轴竖直向下。

图2 主梁测点及其三向加速度传感器方向
主梁下测点X向振动加速度的曲线如图3所示。80 s数据相应的功率谱曲线如图4所示。从图中看到,主梁下测点X向振动较为复杂,含有周期振动和冲击振动的成分。振动能量在低频段所占的比例较大,功率谱峰值曲线主要集中在50 Hz以下。最大峰值所在频率为15.88 Hz。
主梁下测点Y向振动加速度曲线图与相同行程中主梁下测点X向振动相似。振动主要能量分布在50 Hz以内,前10个频谱峰值主要分布在30 Hz以内的频段。
推进缸前端测点及其三向加速度传感器方向如图5所示,加速度传感器布置方向为Y轴沿缸体轴向向后,Z轴竖直向下,X轴方向由右手法则确定。
推进缸前端测点X向振动加速度的曲线如图6所示。80 s数据相应的功率谱曲线如图7所示。从图中看到,推进缸前端测点X向振动较为复杂,含有周期振动和冲击振动的成分。振动能量在低频段所占的比例较大,同时结合图7发现,频谱和功率谱峰值曲线主要集中在100 Hz以下,特别是在50 Hz以下分布密集。最大峰值所在频率为15.15 Hz。

图3 主梁测点的X向振动加速度曲线

图4 主梁下测点X向数据的功率谱

图5 推进缸前端测点及其三向加速度传感器方向

图6 推进缸前端测点X向振动加速度曲线

图7 推进缸前端测点X向的功率谱
推进缸前端测点在Y向、Z向振动加速度曲线图与相同行程中推进缸前端测点X向振动相似。
由上述结果可以看出,TBM推进系统在整个工作过程中,各测点上均在15 Hz附近处存在振动峰值,由于其峰值频率相对固定,为降低系统的振动水平,本文采用被动动力吸振器这种对于较窄频带内的振动具有良好抑制效果的装置来作为TBM推进系统的减振措施。
2 质量放大吸振器
2.1 力学模型
由于TBM推进系统质量巨大,为达到良好的抑振效果,吸振器必须要有足够大的附加质量,然而受限于安装空间等因素,TBM系统吸振器的质量须控制在很小范围。文献[7、8、9]中,分析了支点固定于主系统的杠杆式吸振器,其对缩小吸振器静变形及弹性力的放大有较好的效果,然而对惯性力的放大效果十分有限。为能获得更好的惯性力放大效果,对如图8所示的支点固定的杠杆式吸振器进行分析。
该简化模型中,杠杆支点位置固定不动,并假设杠杆为不可弯曲的刚性梁,且忽略其质量,A1、A2分别为杠杆较长和较短力臂的长度。令η=A1/A2,由几何关系得x2=ηx1,建立系统的动力学模型:
系统动能

系统势能
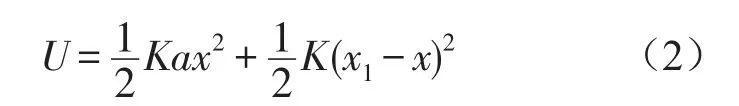
阻尼耗散能

将(1)(2)(3)式代入拉格朗日方程,可得系统的运动微分方程

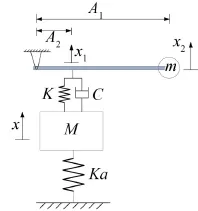
图8 质量放大吸振器系统等效力学模型
其阻尼矩阵和刚度矩阵均与没有利用杠杆原理的传统被动动力吸振器的阻尼矩阵与刚度矩阵相同。由系统动力学方程的惯性矩阵可以看出,由于利用了杠杆原理,吸振器的附加质量由m变为了η2m,即利用杠杆原理可使吸振器的等效附加质量放大η2倍,η为所利用杠杆的力臂之比。
2.2 机构实现与系统频响函数
为实现杠杆的支点位置固定不动,且考虑在TBM推进系统上的安装需求,设计如图9(a)所示的机构以实现杠杆效果。
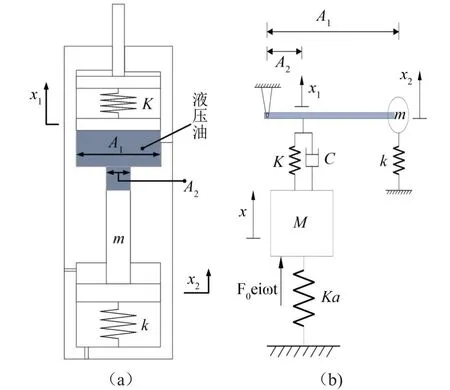
图9 质量放大吸振器机构原理及其简化力学模型
其中,A1为上腔室横截面面积,A2为中间孔道横截面面积。实际工作过程中,假设油液体积不可压缩,并由上下腔室中的活塞密封,通过液压油在腔室中流速的变化来起到杠杆效果。该结构与TBM推进系统的推进油缸并联安装,最上端活塞连接在振动的TBM主梁上,缸体则连接于撑靴之上。实际工作过程中,缸体在轴向可视为固定不动,即实现了杠杆支点位置的固定。惯性力主要由下腔室内的活塞提供,因此忽略上腔室内活塞以及液压油的质量。为保证下腔室内活塞杆的正常运动,下腔室为非封闭设计。
将该吸振器安装于质量为M,刚度为Ka的主系统上后,整个系统的简化力学模型如图9(b)所示,其中,c为吸振器工作时,液压油所产生的阻尼力。建立系统的动力学方程,如式(5)所示

求解该微分方程,即可得到式(6)所示的主系统的稳态振幅响应为
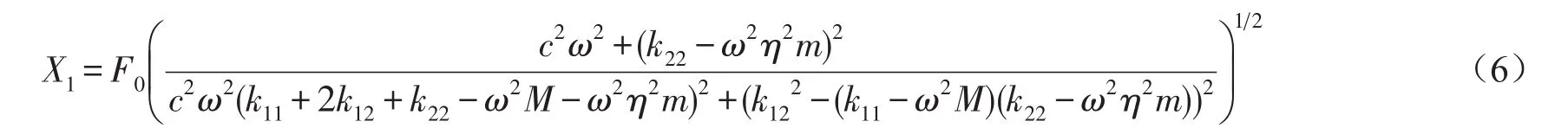
式中kij……i,j=1,2为系统刚度矩阵中相对应的元素。令
将其代入系统的频率响应函数,则可得主系统无量纲化的稳态振幅响应为

3 刚度与阻尼优化
3.1 最优同调条件
由定点理论[10,11]可知,频率响应函数在阻尼分别为零和无穷大时的曲线的交点为一定点,其不随系统阻尼值的变化而变化。
将ς=0代入系统的频率响应函数,可得

将ς=∞代入系统的频率响应函数,可得

设以上两函数的图像交于P、Q两点,则P、Q两点即为系统频率响应函数的定点。
联立(8)(9)两式,即可求出P、Q两点的横坐标值,并将其代入式(7)中,并令频率响应函数在P、Q两点处的纵坐标值相等,则可求出系统的最优同调条件,其结果为

3.2 最优阻尼条件
通过最优同调条件可使系统的频率响应函数的曲线在P、Q两点处等高,不难理解,当曲线在P、Q两点处的斜率为零时所对应的阻尼值即为系统的最优阻尼。将式(10)代入式(7)进行化简,并对g求导,使曲线的斜率分别在P、Q两点处为零,可分别求得在P、Q两点处的最优阻尼,式(11)所示。

设计时,可取二者的平均值,即

式(12)即为系统的最优阻尼条件。
4 TBM推进系统动力吸振实例计算
TBM推进系统上所允许的附加质量被限制在5‰内,故计算时取真实质量比为5‰,即m/M=0.005,η=4,τ=-0.5。TBM推进系统总重100 t,参照实验数据,设计吸振频率为15 Hz,则由式(10)可求得f=0.960 8, k=3.85×106N/m, K=6.17×107N/m由式(11)、式(12)求得最优阻尼比分别对比没有利用杠杆原理的吸振器、利用杠杆原理但无优化吸振器和利用杠杆原理且优化后的吸振器的抑振效果
从图10中的结果可以看出,在采用了质量放大吸振器后,主系统的振动峰值要明显低于采用无质量放大吸振器时的峰值;对于没有进行优化的质量放大吸振器,虽然其在局部频带内的抑振效果要优于经过优化的质量放大吸振器,但其会在其他频带内产生明显的较大的振动峰值。就整个频域范围内来看,经过优化的质量放大吸振器的抑振效果最佳。

图10 三种不同吸振器对系统响应的抑制效果对比
5 结语
通过对某隧道掘进工程中所使用的硬岩掘进设备(TBM)在施工现场的振动情况的测量,发现了TBM推进系统在15 Hz附近处存在着明显的振动峰值,并提出利用动力吸振器来实现对TBM掘进系统的振动抑制,从而提高其掘进效率。
针对TBM推进系统特有的机械结构,通过杠杆原理和定点理论,提出了新型的质量放大动力吸振器方案。该型吸振器可有效的对吸振器的附加质量进行放大,其质量放大系数即为杠杆力臂长度之比的平方。通过其简化的力学模型,推导出该型动力吸振器的最优同调条件和最优阻尼条件。最后,通过TBM推进系统具体的结构参数,得到动力吸振器最优的刚度和阻尼参数,并对比了传统无质量放大吸振器、无优化质量放大吸振器和经过最优设计的质量放大吸振器的抑振效果。结果表明利用杠杆原理的质量放大吸振器的抑振效果要明显优于无质量放大吸振器,而经过优化设计的质量放大吸振器的抑振效果亦要明显优于无优化质量放大吸振器。
[1]B Maidl,L Schmid,W Rits,et al.Hardrock tunnel boring machines[M].Ernst&Sohn,Berlin,2008.
[2]纪昌明,张照煌,叶定海.盘形滚刀刀间距对岩石跃进破碎参数的影响[J].应用基础与工程科学学报,2008,16(2):255-263.
[3]孙伟,凌静秀,霍军周,等.TBM水平支撑不同接触面积下的围岩稳定性分析[J].哈尔滨工程大学学报,2013,34(7):899-906.
[4]K R HONG,H J ZHAO,J D CHANG,et al.Study on dynamic performance of cutter head and cutter system of rocktunnelingsetup[J].AppliedMechanicsandMaterials, 2012,143-144:512-516.
[5]齐征宇,张怀亮,彭欢.TBM液压直管道的非线性动力学特性研究[J].噪声与振动控制,2014,34(3):61-66.
[6]刘泉声,时凯,朱元广,等.TBM盘形滚刀破岩力计算模型研究[J].煤炭学报,2013,38(7):1136-1142.
[7]顾明,陈甦人,项海帆.用于杨浦大桥抖振控制的MTMD研究[J].振动工程学报,1998,11(1):1-8.
[8]M GU,S R CHEN,C C CHANG.Control of windinduced vibrations of long-span bridges by semi-active lever-type TMD[J].Journal of Wind Engineering and IndustrialAerodynamics,2002,90:111-126.
[9]C X LI.Performance Assessment of lever-type tuned mass damper for long-span bridge[J].Journal of HUST,2005, 22(1):98-107.
[10]背户一登著.任明章译.动力吸振器及其应用[M].北京:机械工程出版社,2013.
[11]代林,上官文斌,张少飞.n级动力吸振器的建模及参数优化[J].噪声与振动控制,2012,32(3):45-48.
Optimization of DynamicAbsorbers of Tunnel Boring Machines
LI Xian1,ZOU Xiao-yang2,XU Hai3,ZHENG Hui1,2
(1.Institute of Vibration,Shock and Noise,Shanghai Jiaotong University,Shanghai 200240; 2.Shanghai Key Laboratory of Digital Manufacture for Thin-walled Structures, Shanghai Jiaotong University,Shanghai 200240; 3.China Railway 18 Bureau Group Co.Ltd.,Xi’an 710400,China)
Vibration response of a Tunnel Boring Machine(TBM)in a tunneling engineering was measured.The results showed that there was an intensive vibration response of the TBM during the tunnel boring process and a distinct peak value of the vibration acceleration response of the principal girder near 15 Hz frequency.In order to suppress the vibration of the TBM,a measure using dynamic vibration absorbers(DVA)was proposed.To ensure the vibration reduction effectiveness of the DVA,a sufficiently large additive mass was necessary for the traditional DVA design.Unfortunately,this was impossible due to the tremendous mass of the TBM and very limited available space for DVA installation.In this work, a new DVA design was proposed where the additive mass was amplified by a leverage mechanism.The dynamic equations for the TBM with the new DVA were developed,and the frequency response function was obtained.Furthermore,the stiffness and damping parameters of the proposed DVA were optimized using fixed-point design theory.Finally,the performances of the new DVA and the traditional DVA were compared mutually.It is shown that the new DVA performs much better than the traditional ones in vibration reduction of the TBM system.
vibration and wave;tunnel boring machines(TBM);dynamic vibration absorber;leverage principle; mass amplification effect;fixed-point design theory
TB535
A
10.3969/j.issn.1006-1335.2015.03.041
1006-1355(2015)03-0189-06
2014-10-24
国家重点基础研究发展计划(973计划:2013CB035403)
李献(1989-),男,河北石家庄人,硕士生,主要研究方向:结构动力学分析与减振设计方法。
郑辉,男,博士生导师。E-mail:huizheng@sjtu.edu.cn
