基于Hoek-Brown准则的岩体力学参数确定方法

朱玺玺，陈从新，夏开宗

(中国科学院 a.武汉岩土力学研究所;b.岩土力学与工程国家重点实验室，武汉 430071)

1 研究背景

为了保证岩体工程的开挖既安全稳定又经济合理，需对工程建设的可行性和适宜性进行评价。准确地对各工况的边坡进行稳定分析，以便能够及时对工程加固设计和施工的质量做出反馈。而要准确地获取各工况下边坡稳定系数，不管是运用通常的极限平衡法还是有限元等其它的数值算法，都须获取边坡岩体相关的强度参数。因此，强度参数的获取对边坡岩体工程的变形预测和稳定性评价就显得至关重要。怎样获得可靠的岩体力学参数，一直是岩土工程学者研究的重要课题［1］。在获取岩体力学参数的诸多方法中，最直接、最准确的方法是进行大型现场原位试验，但这种试验需要的周期长、费用高，且还存在着一些尚待解决的技术问题，因此，岩体力学参数的获取仍比较困难，其发展受到一定的限制。

寻求能为众多工程普遍接受的方法，已成为近年来人们关注的另一个目标和趋势。实践证明，以室内岩石力学试验为基准，综合考虑岩体中节理裂隙、地下水和尺寸效应的影响，将岩石力学参数进行修正后换算成岩体力学参数，可以满足工程需要。这类方法中，Hoek-Brown准则由于较全面地反映了岩体的结构特征对岩体强度的影响，是发展最完善的方法［2－3］。为此，本文以湖北宜巴高速公路上的彭家湾软硬岩互层边坡为依托背景，全面地阐述了采用Hoek-Brown准则确定岩体力学参数的方法，所得成果能为其他类似工程求取岩体力学参数提供指导。

2 Hoek-Brown准则的参数评估

2.1 Hoek-Brown强度准则原理

Hoek和Brown在分析Griffith强度理论和修正的Griffith强度理论的基础上，通过对大量的岩块三轴试验资料和岩石现场试验成果的统计分析，并综合考虑了岩体结构、岩块强度、应力状态等多方面的影响，凭借自己在岩石力学方面深厚的理论功底和丰富的实践经验，于1980年第一次提出了最初的Hoek-Brown非线性经验破坏强度准则，即［4］

式中:σ1为岩体破坏时的最大主应力;σ3为岩体破坏时的最小主应力;σc为组成完整岩块试件的单轴抗压强度;mb和s为岩体的材料参数，与其岩性与结构面情况有关，均可表示为地质强度指标GSI(Geological Strength Index)的函数，其估算公式分别为［5］

式中:D为节理岩体遭受破坏和应力松弛受扰动程度的参数，岩体受扰动程度参数D需要根据岩体工程所受扰动程度来确定，取值为=0～1，对于未受扰动的岩体，D=0;对于严重受扰动的岩体，D=1。mi为完整岩块的Hoek-Brown常数，反映岩石的软硬程度，可以通过试验资料或查表获得。GSI为地质强度指标，用来估计不同地质条件下的岩体强度。

从上面的分析可知，在确定岩体力学参数时，关键是确定地质强度指标GSI和岩体扰动程度的参数D，在求取这2种参数过程中，Hoek只是根据定性的描述，然后给出一定的取值，这样所得结果存在着很大的主观性。由于岩体波速有着测试方便、快速和控制范围大等特点，其随岩体介质的变化规律与地质强度指标GSI和岩体扰动参数D在估值上考虑的因素基本一致。所以，国内外学者在运用岩体波速来定量地描述地质强度指标GSI和岩体受扰动程度的参数D的过程中，做了大量的研究［6－8］。本文采用文献［6］的研究成果来确定岩体受扰动程度的参数 D，按式(3)来取值［6］，即

式中Kv为岩体完整性指数，其值为岩体弹性纵波速度与岩块弹性纵波速度比值的平方。

而地质强度指标GSI则按式(4)来取值［2］，即

从上所述，由于地质强度指标GSI及以及岩体受扰动程度的参数D与超声波速之间存在一定的关系，可以在Hoek-Brown准则中引入岩体波速Vp，将式(3)和式(4)代入式(2)便得到由岩体波速确定的mb，s参数关系式为

2.2 岩体单轴抗压和抗拉强度

在获得岩体变形模量参数Em后，令σ3=0代入式(1)可求得岩体的单轴抗压强度为

对于完整岩石，s=1，则 σcm=σc，即为岩块单轴抗压强度;对于完全破碎的岩石，s=0，则σcm=0。

将σ1=0代入方式(1)中，将所得的二次方程中对σ3求解，可解得岩体的单轴抗拉强度为

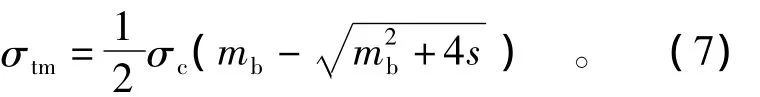
2.3 岩体变形模量

岩体变形模量Em是数值模拟计算中的一个重要指标。1988年，Hoek和Brown在考虑地质强度指标GSI和完整岩块单轴抗压强度σc(≤100 MPa)基础上，提出了最初的变形模量估算Em(单位为GPa)关系式为

2002年，经过 Hoek，Carranza-Torres和 Corkum的修正，引入了岩体受扰动程度的参数D，综合考虑了爆破破坏和应力松弛对岩体的影响。修正后的变形模量Em可用式(9)，进行估算，即

将式(2)和式(3)代入式(9)便得到由岩体波速确定岩体变形模量关系式为

2.4 岩体抗剪强度参数

2.4.1 岩体单轴抗压和抗拉强度法

Mohr-Coulomb准则推导了用岩体的黏聚力Cm和内摩擦角φm表示岩体单轴抗压强度σcm和岩体单轴抗拉强度 σtm为［9］

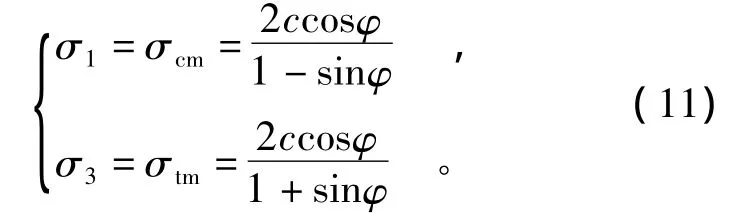
根据上式可以推出内摩擦角φm和黏聚力cm的表达式为

2.4.2 非线性关系算法

从Mohr-coulomb准则出发，式(13)为利用大、小主应力σ1和σ3来表示滑动面上的正应力σ和剪应力τ的关系，进而导出式(14)。

通过对式(1)及式(14)求导推出莫尔强度包络线方程［10］，即滑动面上的正应力σ和剪应力τ为

式中 τm=(σ1－σ3)/2。

将相应的三轴试验数据σ1和σ3代入式(15)和式(16)，就能在τ－σ平面上得到莫尔强度包络线上τ和σ的关系点坐标。Hoek和Brown提出利用σ3值在(0，0.25σc)范围内取8个以上等间距数值来获取岩体的内摩擦角φm和黏聚力cm值，由于岩体的抗剪强度，尤其是扰动岩体的抗剪强度参数多为非线性关系，故Hoek建议的抗剪强度非线性关系为［11］

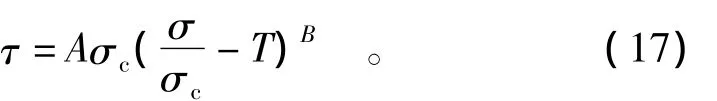
式中:τ为岩体的剪切强度;σ为岩体法向应力;A，B均为待定常数，可通过回归确定或者由岩体质量与经验常数之间的关系表求得。改写上述方程，则变换为

式中:y=Int/σc，x=In(σ/σc－T)，a=B，b=In A，T=，常数A和B可由最小二乘法线性回归确定，即

拟合决定系数为

在任一σ时非线性莫尔强度包络线的内摩擦角φm和黏聚力cm可由式(17)求导得，即

2.4.3 回归分析法

Hoek 和 Brown 等［5，11］研究表明:σm＜σ3＜σ3max(最小主应力的最大值)时，Mohr-Coulomb强度准则曲线与 Hoek-Brown准则曲线非常吻合，可以将式(1)采用回归分析法近似的拟合为Mohr-Coulomb屈服准则相似的公式，即

根据Mohr-Coulomb强度准则的应力圆和曲线之间的关系，可得由最大主应力σ1和最小主应力σ3来表示Mohr-Coulomb强度破坏准则的另一有用公式，即

亦即

将式(22)和式(23)对比可得

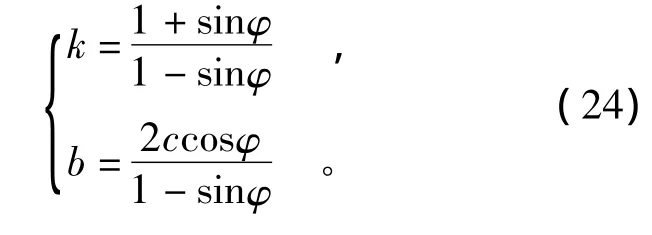
式中:

上述3种经验法计算都是以Hoek-Brown强度准则为基础的，由于几种方法适用性、考虑因素、计算参数等条件的不同，所得计算结果应综合起来考虑，认为是最合理的。

3 工程应用

彭家湾上覆堆积体及其下伏软硬岩互层这种缓倾复合介质边坡是沪蓉国道主干线湖北宜昌至巴东高速公路上软硬岩交互型崩滑体中最为典型的一处，严重地影响了公路的安全［12－13］，表1为岩块单轴抗压强度、岩体完整性系数和岩体波速。对场区岩块力学参数进行工程弱化处理时，首先根据现场岩体的岩性情况，由文献［14］查得的mi值、表1所列出的岩块强度参数、岩体完整性指数和波速，计算出相应的Hoek-Brown计算参数，见表2。在获得Hoek-Brown计算参数之后，运用式(6)至式(10)计算得到岩体的单轴抗压、抗拉强度及变形模量等力学参数，见表3。在获得岩体的单轴抗压和单轴抗拉强度之后，借助式(12)给出了运用岩体单轴抗压和抗压强度法确定的岩体抗剪强度力学参数，见表4。

表1 岩块单轴抗压强度、完整性系数和岩体波速Table 1 Uniaxial compressive strength of rock，integrity factor and wave velocity of rock mass

表2 Hoek-Brown计算参数Table 2 Hoek-Brown calculation parameters

表3 岩体单轴抗压、抗拉强度及变形模量Table 3 Uniaxial compressive strength，tensile strength and deformation modulus of rock mass

计算中的有关说明:

(1)非线性关系算法。选取σ3的范围0＜σ3＜0.25σc，在 σ3的取值区间内从 0逐渐增大到{［0.25σc］－1}取 8 组等间距分布的 σ3，用式(1)求取一系列的相应的σ1，借助式(17)求取不同法向应力σ下对应的剪应力τ，通过线性回归的方法确定一定应力范围内线性化后c值和φ作为岩体破坏时总体或平均c值和φ值，其计算结果见表4。

(2)回归分析法。在 σ3取值区间(0，0.25σc)内从0逐渐增大到0.25σc取8组等间距分布的σ3。用式(1)计算出相应的σ1值，再运用式(22)至式(25)进行回归计算分析，其计算结果见表4。

表4 岩体抗剪强度力学参数计算结果及其推荐值Table 4 Calculated shear strength parameters of rock mass and recommended values

4 计算结果分析

图1为用Hoek-Brown法绘制的场区岩体莫尔强度包络线，图中下标①代表中风化粉砂质泥岩，②代表中风化石英砂岩，③代表微风化粉砂质泥岩，④代表微风化石英砂岩，下同。图2为正应力σ与瞬时黏聚力c、瞬时内摩擦角φ的关系曲线。图3为岩体单轴抗压和抗拉强度法、非线性关系算法和线性拟合回归分析法得出的岩体黏聚力c值和内摩擦角φ值比较。

(1)从图1中可以看出，用Hoek-Brown法绘制的莫尔强度包络线上某点的切线坐标τ上的截距和切线斜率，即为正应力σ对应的瞬时黏聚力c和瞬时内摩擦角φ，与横坐标σ的负方向的交点，即为岩体单轴抗拉强度σtm，非线性莫尔强度包络线的截距随着正应力σ的增大而增大，即瞬时黏聚力c逐渐增大(见图2(a))，而斜率随着正应力σ的增大而减小，即瞬时内摩擦角 φ则逐渐减小(见图2(b))。

图1 用Hoek-Brown法绘制的莫尔强度包络线Fig.1 Mohr strength envelopes by Hoek-Brown criterion

图2 正应力σ与瞬时黏聚力c、瞬时内摩擦角φ的关系曲线Fig.2 Curves of normal stress σ vs.instantaneous cohesive force c and instantaneous internal friction angleφ

所以，采用Hoek-Brown准则确定岩体力学参数时，正应力σ的确定是关键:应在实际应用范围内确定正应力σ，这样所得的岩体力学参数才与实际情况比较接近。

(2)通过c值的计算结果对比分析可知(图3(a))，改进的非线性关系算法与线性拟合回归分析法相比，平均相对误差为16.14%，差别较小，说明两者在c值上基本等效;与岩体单轴抗拉和抗压强度法得出的结果相比，两者在c值上的平均相对误差为88.7%，差别比较大。通过φ值的计算结果对比分析可知(图3(b))，非线性关系算法与线性拟合回归分析法相比，平均相对误差为8.61%，相差较小，说明两者在φ值上基本等效;与岩体单轴抗拉和抗压强度法得出的结果相比，两者在φ值上的平均相对误差为138.50%，差别非常大，说明两者在φ值上基完全不一致;究其原因是:岩体单轴抗拉和抗压强度法是从Mohr-Coulomb准则出发推导的，在拉应力区莫尔强度包络线是曲率较大的曲线，而式(12)是按直线包络线算得的，所得到的岩体单轴抗拉强度σtm的理论值远大于实测值，因而Mohr-Coulomb准则在本质上不能描述岩体在拉应力区和低应力区的真实强度特征。

图3 3种方法确定的岩体黏聚力、内摩擦角比较Fig.3 Cohesive force and internal friction angle of rock mass obtained from three methods

从以上分析和论述可知，非线性关系算法和线性拟合回归分析法所得的结果是可行的，而岩体单轴抗拉和抗压强度法所得的结果是不可行的，故取非线性莫尔强度包络线法和线性拟合回归分析法两者的平均值，作为场区岩体的抗剪强度参数的推荐值，其结果一并列入表4。

5 数值模拟计算结果

限于篇幅，本文只列出了采用FLAC3D模拟场区在施工开挖降雨饱和和河流切割+降雨饱水2种工况下塑性区分布，如图4所示。

图4 2种不同工况下场区的塑性区分布Fig.4 Distributions of plastic zone in two operation conditions

从图4(a)可以看出，施工开挖+降雨饱和后坡面及堆积体四周存在明显的塑性区:在堆积体的前缘及左右发展了零星分布的剪切塑性区，在堆积体的后缘存在着拉伸破坏区;而从图4(b)可以看出，河谷下切的情况下，在坡表堆积体的后缘形成拉伸破坏带，在巨厚层泥岩中形成不连续的剪切破坏带，剪切破坏带基本已贯通。所以，在河流下切+降水饱和情况下，边坡最有可能的破坏模式为沿着巨厚泥岩层的顺层滑动。而从现场了解到，在降雨的情况下，在堆积体的四周有局部崩滑的可能性，如在堆积体后缘西侧在1982年雨季发生了一小处土层坍滑，平面上呈圈椅状，面积7 150 m2;另外，通过室内物理模型试验表明，在河流切割作用下，不断地注水软化巨厚泥岩层，边坡的变形破坏模式为沿着为巨厚软岩层滑动［15］。

从上分析可知，数值模拟计算结果与现场边坡的实际变形破坏特征，以及室内物理模型试验得出的结果基本是一致的，所以可以认为根据本文计算所推荐的岩体力学参数进行工程数值模拟，其结果是合理的。

6 结论

(1)非线性关系算法和线性拟合回归分析法所得的结果是可行的，而岩体单轴抗拉和抗压强度法所得的结果是不可行的，究其原因是:Mohr-Coulomb准则不能描述岩体在拉应力区和低应力区的真实强度特征。

(2)应用Hoek-Brown强度准则对场区岩块力学参数工程弱化处理结果，表明:由于岩体中弱节理面、断裂构造等因素的影响，使得岩体的强度及变形模量较相应的岩块来说要低得多。

(3)采用根据本文计算所推荐的岩体力学参数进行工程数值模拟，其结果与现场调查观测和室内模型试验情况基本一致。所以，倘若未开展大型现场原位试验，直接运用Hoek-Brown准则来估算岩体力学参数基本上可以满足工程实践所需的精度要求。

［1］苏永华，封立志，李志勇，等.Hoek-Brown准则中确定地质强度指标因素的量化［J］.岩石力学与工程学报，2009，28(4):679－ 686.(SU Yong-hua，FENG Li-zhi，LI Zhi-yong，et al.Quantification of Elements for Geological Strength Index in Hoek-Brown Criterion［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28(4):679－686.(in Chinese))

［2］夏开宗，陈从新，周意超，等.基于E.Hoek建议的非线性关系求取岩体抗剪强度的算法及工程应用［J］.岩土力学，2014，35(6):1743－1750.(XIA Kai-zong，CHEN Cong-xin，ZHOU Yi-chao，et al.The New Algorithm of Obtaining Shear Strength of Rock Mass Based on Nonlinear Equation Proposed by E.Hoek and Its Application to Engineering［J］.Rock and Soil Mechanics，2014，35(6):1743－1750.(in Chinese))

［3］夏开宗，陈从新，刘秀敏，等.基于岩体波速的Hoek-Brown准则预测岩体力学参数的方法及工程应用［J］.岩石力学与工程学报，2013，32(7):1458－1466.(XIA Kai-zong，CHEN Cong-xin，LIU Xiu-min，et al.Estimation of Rock Mass Mechanical Parameters Based on Ultrasonic Velocity of Rock Mass and Hoek-Brown Criterion and Its Application to Engineering［J］.Chinese Journal of Rock Mechanics and Engineering，2013，32(7):1458－1466.(in Chinese))

［4］HOEK E，BROWN E T.Underground Excavation in Rock［M］.London:Institute of Mining and Metallurgy，1980.

［5］HOEK E，CARRANZA-TORRES C T，CORKUM B.Hoek-Brown Failure Criterion:2002Edition［C］//Proceedings of the 5th North American Rock Mechanics Symposium.Toronto，Canada，July 7－10，2002:267－273.

［6］闫长斌，徐国元.对Hoek-Brown公式的改进及其工程应用［J］.岩石力学与工程学报，2005，24(22):4030－4035.(YAN Chang-bin，XU Guo-yuan.Modification of Hoek-Brown Expressions and Its Application to Engineering［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24(22):4030－4035.(in Chinese))

［7］巫德斌，徐卫亚.基于Hoek-Brown准则的边坡开挖岩体力学参数研究［J］.河海大学学报:自然科学版，2005，33(1):89－ 93.(WU De-bin，XU Wei-ya.Mechanical Parameters of Rock Slope Excavation Based on Hoek-Brown Criterion［J］.Journal of Hohai University(Natural Sciences)，2005，33(1):89－ 93.(in Chinese))

［8］彭国城.Hoek-Brown强度准则中扰动系数研究［D］.昆明:昆明理工大学，2011.(PENG Guo-cheng.Disturbance Factor in Hoek-Brown Strength Criterion［D］.Kunming:Kunming University of Science，2011.(in Chinese))

［9］徐志英.岩石力学［M］.北京:中国水利水电出版社，1991:37－ 45.(XU Zhi-ying.Rock Mechanics［M］.Beijing.China Water Power Press，1991:37－45.(in Chinese))

［10］宋建波，张倬元，于远忠，等.岩体经验强度准则及其在地质工程中的应用［M］.北京:地质出版社，2002:12－ 22.(SONG Jian-bo，ZHANG Zhuo-yuan，YU Yuan-zhong，et al.Empirical Rock Strength Criterion and Its Application to Geological Engineering［M］.Beijing:Geology Press，2002:12－22.(in Chinese))

［11］胡盛明，胡修文.基于量化的GSI系统和Hoek-Brown准则的岩体力学参数的估计［J］.岩土力学，2011，32(3):861－865.(HU Sheng-ming，HU Xiu-wen.Estimation of Rock Mass Parameters Based on Quantitative GSI System and Hoek-Brown Criterion［J］.Rock and Soil Mechanics，2011，32(3):861－865.(in Chinese))

［12］夏开宗，陈从新，鲁祖德，等.考虑水力作用的顺层岩质边坡稳定性图解分析［J］.岩土力学，2014，35(10):2985－2993.(XIA Kai-zong，CHEN Cong-xin，LU Zu-de，et al.Analysis of Stability Diagram of Rock Bedded Slope under Hydraulic Pressure［J］.Rock Mechanics and Soil Mechanics，2014，35(10):2985－2993.(in Chinese))

［13］夏开宗，陈从新，刘秀敏，等.水力作用下缓倾顺层复合介质边坡滑移破坏机制分析［J］.岩石力学与工程学报，2014，33(增 2):3766－ 3775.(XIA Kai-zong，CHEN Cong-xin，LIU Xiu-min，et al.Analysis of Sliding Failure Mechanism of Gently Inclined Bedding Compound Rock Mass Slope under Hydraulic Pressure［J］.Chinese Journal of Rock Mechanics and Engineering，2014，33(Sup.2):3766－3775.(in Chinese))

［14］MARINOS P，HOEK E.GSI:A Geologically Friendly Tool for Rock Mass Strength Estimation［C］//Proceedings of the 2000 International Conference on Geotechnical and Geological Engineering.Melbourne，Australian，November 19－24，2000:1422－1442.

［15］宋娅芬，陈从新，郑 允，等.缓倾软硬岩互层边坡变形破坏机制模型试验研究［J］.岩土力学，2015，36(2):487－ 494.(SONG Ya-fen，CHEN Cong-xin，ZHENG Yun，et al.Model Experimental Study of Deformation and Failure Mechanism of Low-angled Slopes with Interbeddings of Soft and Hard Rocks［J］.Rock and Soil Mechanics，2015，36(2):487－494.(in Chinese))