砂土液化等级预测的主成分-Logistic回归模型

王军龙

(西安铁路职业技术学院 土木工程系，西安 710600)

1 研究进展

砂土液化是在循环往复荷载作用下，饱和砂土层孔隙水位升高，有效应力降低，造成地基承载力部分或者全部丧失，形成的一种破坏性严重的区域性地质灾害。20世纪60年代以来，几次大的地震，如日本新泻地震(1964)、美国阿拉斯加地震(1964)、中国唐山大地震(1978)以及神户大地震(1995)、汶川特大地震(2008)等均因砂土液化导致堤防或建筑物大规模的破坏，给人类造成了巨大的经济损失，砂土液化问题引起了工程界的广泛关注［1－2］。考虑单因素判定砂土液化具有一定的片面性，多因素综合评判就成为砂土液化判别分析的一种可行方法。据此，国内外的学者提出了多种综合预测模型和方法，如神经网络模型、支持向量机模型、模糊综合评价法、距离判别法、投影寻踪模型、分形-插值模型［3－9］等。

总结上述模型和方法，可以将其分为2种类型:①以砂土液化分类标准为基础采用一定的数学方法建立模型，这类模型和方法主要包括模糊综合评价法、投影寻踪模型和分形-插值模型，其中投影寻踪模型和分形-插值模型将砂土分类标准直接转化为数学表达式，易于使用，这类模型的有效性依赖于分类标准的准确性;②以一定的砂土液化样本数据为基础，对已有的模型和方法进行训练，从而建立砂土液化预测模型，模型的有效性依赖于训练样本的数量，这类模型和方法主要有神经网络模型、支持向量机模型和距离判别法等。

从模型的通用性和实用性考虑，具有一定数学表达式的模型更易于被理解和应用，其只需将实际数据输入数学表达式中即可计算出预测结果。为了建立简单实用的砂土液化预测模型，本文结合主成分分析和Logistic回归模型来描述砂土液化等级与影响因素之间的映射关系，建立了砂土液化预测的数学表达式。根据数据样本的不同，该模型可以实现上述2种类型，即砂土液化分类标准的数学表达，以及砂土液化实例数据的经验表达。最后，工程实例分析结果显示，本文建立的砂土液化预测模型简单实用，预测效果良好，可以在工程中推广应用。

2 基本方法

对于砂土液化预测问题，砂土液化等级为类别变量［9］(不液化(Ⅰ)、轻微液化(Ⅱ)、中等液化(Ⅲ)、严重液化(Ⅳ)4个等级)，砂土液化指标为连续变量，对于这种连续变量到类别变量之间的函数关系，可以采用Logistic回归分析进行描述。由于砂土液化指标之间具有高度的相关性，直接建立Logistic模型，可能导致模型不稳定、解释上的冲突等［10］。为此，本文在建立Logistic回归模型之前，采用主成分分析降低指标之间的相关性，将多个指标综合为少数几个彼此独立的主成分，从而避免多重共线性的影响。

2.1 主成分分析

主成分分析是一种将多维数据进行降维处理，简化为少数几个不相关的综合指标(主成分)的多元统计分析方法。其建模过程具体如下:

(1)数据预处理。假设有m个样本(i=1，2，…，m)，n 个指标(j=1，2，…，n)，对原始数据 X=进行均值化处理，可保留数据内的变异信息［11］:

(2)计算均值化数据的协方差矩阵S=(sij)n×n。

(3)计算协方差矩阵的特征值和特征向量。S的n个特征值记为:λ1≥λ2≥…≥λn，标准化特征向量为ajj=(aj1，aj2，…，ajn)，则第 i个样本的第 j个主成分为

2.2 Logistic回归模型

Logistic回归分析的目的是建立经验公式，以便由自变量预测因变量概率分布。令y=1，2，3，4表示砂土液化的4个等级。令q1=p(y≤1)，q2=p(y≤2)，…，q3=p(y≤3)，常用的 Logistic回归模型是［12］:

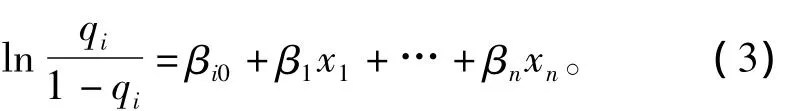
式中:βi0为截距，i=1，2，…，4;β1，…，βn为斜率系数;x1，…，xn为自变量。

由已有观测值能估计出 βi0，β1，…，βn，从而砂土液化各等级的概率表达式:

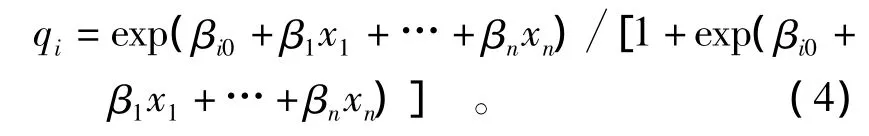
这时对于给定的自变量x1，…，xn的值，由回归方程可以预测 q1，q2，q3，再由 p(y=1)=q1，p(y=2)=q2－q1，…，p(y=3)=q3－ q2，p(y=4)=1－q3可以预测各砂土液化等级概率。根据各类别的概率，由可以确定响应变量属于类别y=l。

3 砂土液化等级预测的主成分-Logistic回归模型

3.1 类型Ⅰ:砂土液化等级的数学表达

首先本文建立第1种类型的主成分-Logistic回归模型，即模型的建立以砂土液化等级分类标准为基础，应用效果完全依赖于砂土液化等级分类标准的准确性。

3.1.1 评价指标与分类标准

影响砂土液化的因素很多，但大体上可分为3大类:第1类是砂土特性，如土的种类、颗粒组成和密实度;第2类是土层埋藏条件;第3类是地震因素或称地震条件。参考以往研究，选择震级M，地面加速度最大值gmax，标贯击数 N63.5，比贯入阻力 Ps，相对密度Dr，平均粒径D50，地下水位dw7个因素作为评价指标。各指标的分类标准详见文献［9］。

3.1.2 生成样本数据

由于本文模型的建立和参数的确定是由数据驱动，因此需要利用砂土液化分类标准来生成数据作为建模基础。由于正态分布是自然界中最常见的分布形式之一，按照各指标的分类标准，每个指标在每个等级范围内按照正态分布随机产生20个样本，其中分布参数均值和标准差(3σ原理)按照下式确定:

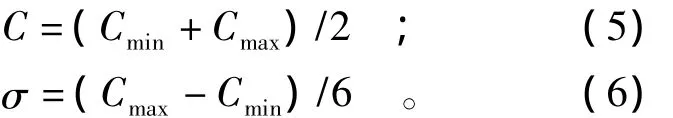
式中:Cmax和Cmin分别为等级最大值和最小值为均值，σ为标准差。

采用Matlab软件normrnd()函数即可实现，对于每个指标采用同一组随机数值，共形成80个评价样本，将不液化(Ⅰ)、轻微液化(Ⅱ)、中等液化(Ⅲ)、严重液化(Ⅳ)分别赋予响应值 4，3，2，1，具体如表1所示。

3.1.3 建立预测模型

首先按照本文介绍的主成分分析步骤，计算得到协方差矩阵的特征值为0.002，0.006，0.010，0.018，0.019，0.061，2.267，特征值 2.267 累计方差贡献率为95.1%＞85%，因此取其对应的特征向量a=(－0.166，－0.366，0.497，0.388，0.425，0.338，0.382)。根据式(1)和式(2)得到主成分计算公式为

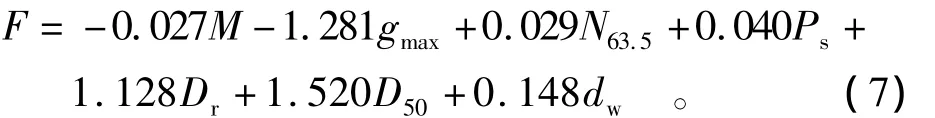
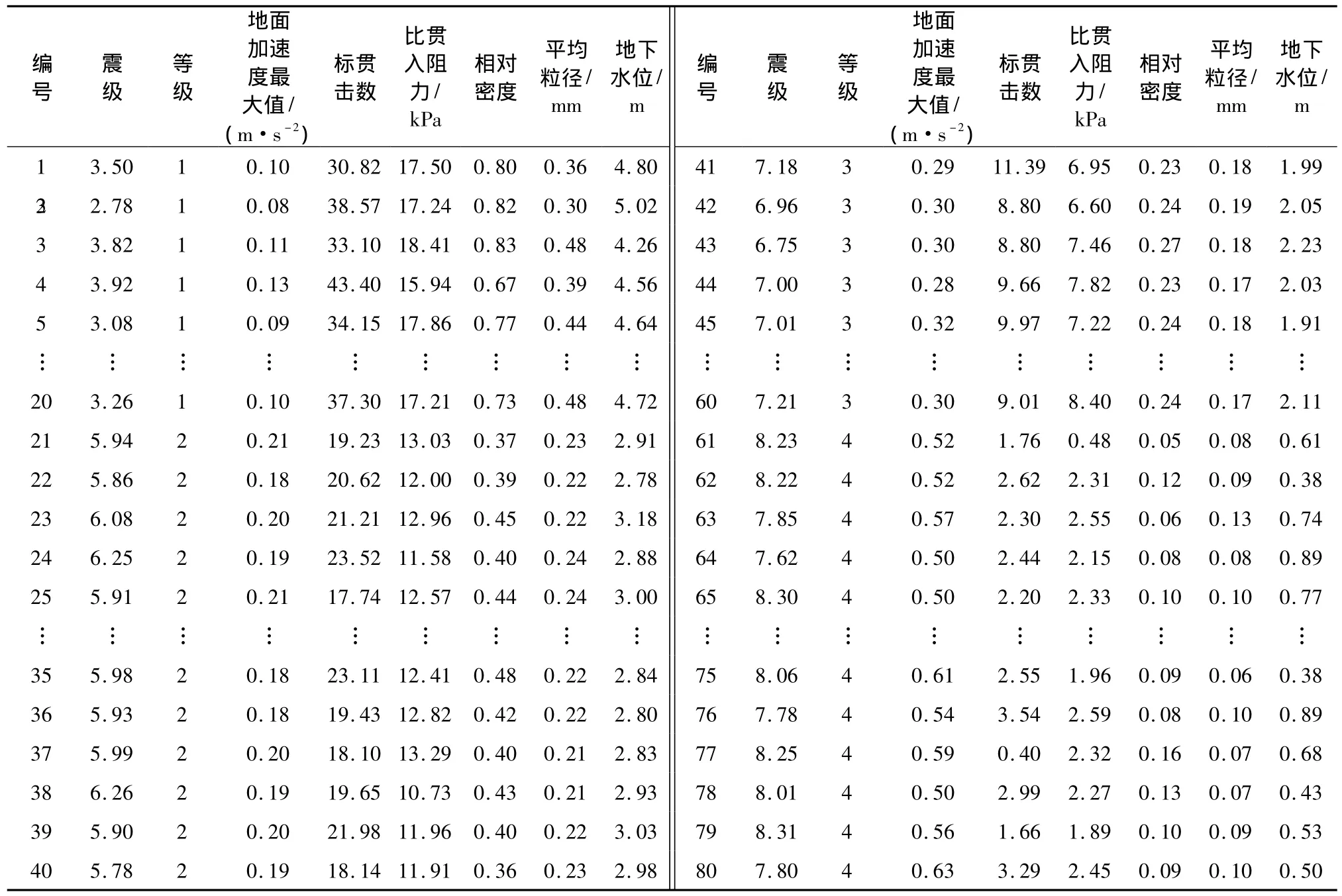
表1 样本数据Table 1 Sample data

根据式(7)可计算各样本对应的主成分值，并用于建立Logistic回归模型。获得样本的主成分值以后，采用Logistic模型建立各样本对应的主成分与经验等级(响应值)之间的函数关系。以SPSS软件实现Logistic模型参数的求解，具体可以参阅相关软件的介绍资料，本文不再复述软件求解过程，得到模型表达式如下:

将各指标实测值代入式(8)至式(11)中即可计算砂土液化属于各等级的概率，从而确定砂土液化等级。Logistic回归模型对上述样本的拟合结果与实际结果完全一致，说明其可以很好地表达砂土液化等级分类标准。

3.2 类型Ⅱ:砂土液化实例的经验表达

上述第1种类型的主成分-Logistic回归模型实现了砂土液化等级分类标准的数学表达，但是很容易发现砂土液化等级分类标准随机产生的样本完全满足所有指标的分级标准，而实际工程中，许多指标数据并不可能同时属于某个等级，并且分类标准的划分具有主观性。下面以砂土液化实例作为样本数据来建立主成分-Logistic回归模型，从理论上讲这类模型应该更符合实际，但是由于样本数量的限制，也不易达到理想的预测效果。

3.2.1 评价指标和样本数据

同样采用上述7个因素作为评价指标，采用文献［13］中提供的25组数作为分析样本，具体数据详见文献［13］。其中前20组数据作为建模样本数据，后5组数据则作为检验样本，以检验模型的预测效果。

3.2.2 建立模型

以20组建模样本数据，按照本文介绍的主成分分析步骤，计算得到协方差矩阵的特征值为0.016，0.036，0.044，0.114，0.185，0.355，0.734，最大的前3个特征值累计方差贡献率为85.8%＞85%，因此取其对应的特征向量计算前3个主成分。根据式(1)和

式(2)得到主成分计算公式为

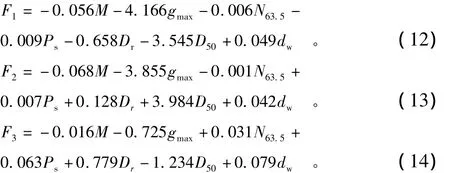
根据以上各式可计算各样本对应的主成分值，并用于建立Logistic回归模型。获得了样本的主成分值以后，采用Logistic模型建立各样本对应的主成分与经验等级(响应值)之间的函数关系。以SPSS软件实现Logistic模型参数的求解，得到模型表达式如下:

将各指标实测值代入式(15)至式(18)中即可计算砂土液化属于各等级的概率，从而确定砂土液化等级。Logistic回归模型对前20个样本的拟合结果与实际结果完全一致，说明其可以很好地表达砂土液化等级与砂土液化指标之间的经验关系。

4 工程应用

下面以实例数据验证和比较上述2种类型的主成分-Logistic回归模型对砂土液化等级的预测效果。由于第1种类型的主成分-Logistic回归模型采用的是分类标准生成的数据，首先以其对文献［13］中提供的25组数据进行预测，检验预测效果，并与分形-插值模型［9］和可拓物元模型［13］进行对比分析。本文仅列出了3种预测结果与实际结果存在差异的样本，见表2。

从表2的预测结果可以看出，本文所建立的主成分-Logistic回归模型与可拓物元模型具有相同的预测效果，都仅出现了2处与实际不一致的地方，预测准确率92%，而分形－插值模型出现了3处与实际不一致的地方，预测准确率88%，稍低于主成分-Logistic回归模型。上述结果说明了本文所建立的第一种类型的主成分-Logistic回归模型预测效果良好，可以使用。

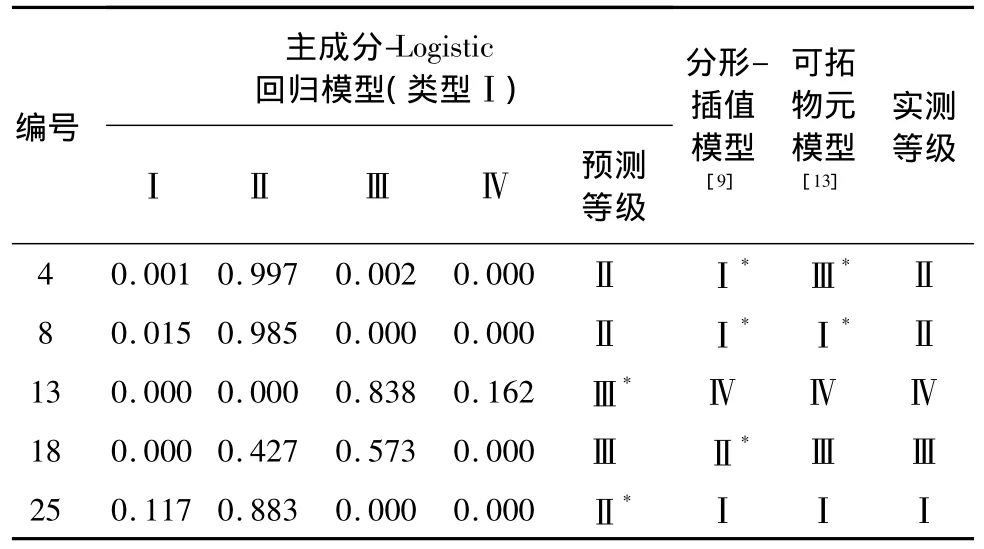
表2 样本实测值和不同模型的预测结果Table 2 Measured values of samples and model-predicted results

其次，以5组检验样本数据对第2种类型的主成分-Logistic回归模型进行检验，并与第1种类型的主成分-Logistic回归模型进行对比分析，结果见表3。

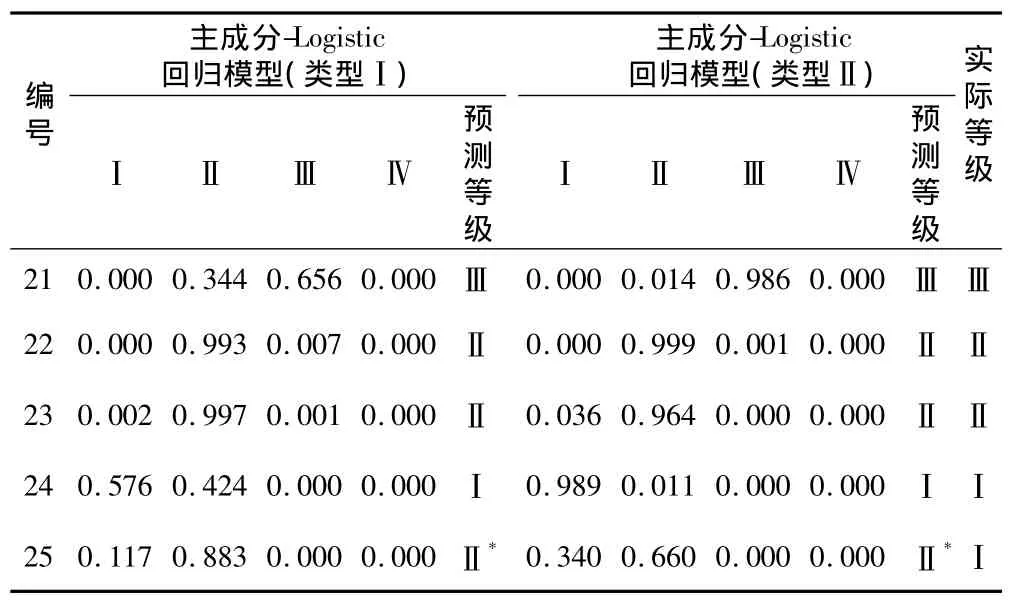
表3 2种类型的主成分-Logistic回归模型预测结果Table 3 Predicted results of two types of PCA-Logistic models

从表3的结果可以看出，2种类型的主成分-Logistic回归模型对样本的预测等级完全一致，仅最后一个样本与实际结果存在差异，从对各等级的概率结果来看，第2种类型的主成分-Logistic回归模型计算样本25属于等级Ⅰ的概率更大(0.340＞0.117)，说明样本25更偏向于等级Ⅰ，从这个角度来看，第2种类型的主成分-Logistic回归模型预测结果确实更符合实际。如果能利用更多的实例数据，相信可以得到更好的预测效果。

5 结论

(1)现有砂土液化等级的多指标预测模型可以分为2种类型:第1类以砂土液化等级分类标准为基础，预测效果依赖于分类标准的准确性;第2类以实例数据为基础，预测效果依赖于样本的数量。

(2)根据砂土液化分类标准生成样本数据，以主成分分析对数据进行降维处理，以Logistic模型描述砂土液化等级与影响因素之间的映射关系(分类标准)，建立了第1种类型的主成分-Logistic回归模型，工程实例分析结果显示该模型预测效果良好，可以在实际中应用。

(3)以工程实例数据作为训练样本建立第2种类型的主成分-Logistic回归模型，用于描述砂土液化等级与影响因素之间的经验关系，与第1种类型的主成分-Logistic回归模型的对比结果显示，第2种类型的主成分-Logistic回归模型预测结果更符合实际情况，在具有较多实例数据时，其更具有应用价值。

［1］任红梅，吕西林，李培振.饱和砂土液化研究进展［J］.地震工程与工程振动，2007，27(6):166－174.(REN Hong-mei，LV Xi-lin，LI Pei-zhen.Advances in Liquefaction Research on Saturated Soils［J］.Journal of Earthquake Engineering and Engineering Vibration，2007，27(6):166－174.(in Chinese))

［2］勾丽杰，刘家顺.RBF神经网络模型在砂土液化判别中的应用研究［J］.长江科学院院报，2013，30(4):76－81.(GOU Li-jie，LIU Jia-shun.Application of RBF Neural Network Model to Evaluating Sand Liquefaction［J］.Journal of Yangtze River Scientific Research Institute，2013，30(4):76－81.(in Chinese))

［3］刘年平，王宏图，袁志刚，等.砂土液化预测的Fisher判别模型及应用［J］.岩土力学，2012，33(2):554－557.(LIU Nian-ping，WANG Hong-tu，YUAN Zhigang，et al.Fisher Discriminant Analysis Model of Sand Liquefaction and Its Application［J］.Rock and Soil Mechanics，2012，33(2):554－557.(in Chinese))

［4］陈国兴，李方明.基于径向基函数神经网络模型的砂土液化概率判别方法［J］.岩土工程学报，2006，28(3):301－ 305.(CHEN Guo-xing，LI Fang-ming.Probabilistic Estimation of Sand Liquefaction Based on Neural Network Model of Radial Basis Function［J］.Chinese Journal of Geotechnical Engineering，2006，28(3):301－305.(in Chinese))

［5］陈荣淋，林建华，黄群贤.支持向量机在砂土液化预测中的应用研究［J］.中国地质灾害与防治学报，2005，16(2):15－18.(CHEN Rong-lin，LIN Jianhua，HUANG Qun-xian.Application of the Support Vector Machine in Prediction of Sand Liquefaction［J］.The Chinese Journal of Geological Hazard and Control，2005，16(2):15－18.(in Chinese))

［6］薛新华，张我华，刘红军.砂土地震液化的模糊综合评判法［J］.重庆建筑大学学报，2006，28(1):55－58.(XUE Xin-hua，ZHANG Wo-hua，LIU Hong-jun.Comprehensive Fuzzy Evaluation Method for Sand Liquefaction［J］.Journal of Chongqing Jianzhu University，2006，28(1):55－58.(in Chinese))

［7］金志仁.基于距离判别分析方法的砂土液化预测模型及应用［J］.岩土工程学报，2008，30(5):776－780.(JIN Zhi-ren.Prediction of Sand Liquefaction Based on Distance Discriminant Analysis and Its Application［J］.Chinese Journal of Geotechnical Engineering， 2008，30(5):776－780.(in Chinese))

［8］汪明武，金菊良，李 丽.基于实码加速遗传算法的投影寻踪方法在砂土液化势评价中的应用［J］.岩石力学与工程学报，2004，23(4):631－634.(WANG Ming-wu，JIN Ju-liang，LI Li.Application of PPMethod Based on RAGA to Assessment of Sand Liquefaction Potential［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(4):631－634.(in Chinese))

［9］王 威，苏经宇，马东辉，等.饱和砂土地震液化判别的分形插值模型［J］.世界地震工程，2012，28(1):118－ 124.(WANG Wei，SU Jing-yu，MA Dong-hui，et al.Fractal Interpolation Model of Seismic Liquefaction Discrimination of Saturated Sandy Soil［J］.World Earthquake Engineering，2012，28(1):118－124.(in Chinese))

［10］袭炯良，郏剑宁，张 扬.主成分改进的logistic回归模型方法在流行病学分析中的应用［J］.中国热带医学，2005，5(2):207－209.(QIU Jiong-liang，ZHENG Jian-ning，ZHANG Yang.Application of Modified Logistic Regression Model in the Analysis of Epidemiology［J］.China Tropical Medicine，2005，5(2):207－209.(in Chinese))

［11］叶双峰.关于主成分分析做综合评价的改进［J］.数理统计与管理，2001，20(2):52－61.(YE Shuangfeng.The Application and Consideration about Principal Component Analysis［J］.Application of Statistics and Management，2001，20(2):52－61.(in Chinese))

［12］吴令云，吴家祺，吴诚鸥，等.MINITAB软件入门:最易学实用的统计分析教程［M］.北京:高等教育出版社，2012.(WU Ling-yun，WU Jia-qi，WU Cheng-ou，et al.MINITAB Software Starter Guide:The Easiest and Most Practical Course for Statistical Analysis［M］.Beijing:Higher Education Press，2012.(in Chinese))

［13］陈荣淋.基于可拓学和支持向量机理论的砂土液化势综合评价研究［D］.厦门:华侨大学，2004.(CHEN Ronglin.Research on Assessment of Sand Liquefaction Potential Based on Extenics and Support Vector Machine［D］.Xiamen:Huaqiao University，2004.(in Chinese))