基于时移小波-灰色理论的边坡位移预测模型研究

郭海庆，张 敏，黄 涛，艾纯斌

(1.河海大学a.岩土工程科学研究所;b.岩土力学与堤坝工程教育部重点实验室，南京 210098;2.中国市政工程东北设计研究总院有限公司海南洋浦分公司，海南洋浦 570125)

1 研究背景

边坡变形稳定性问题一直是岩土工程领域备受关注的问题之一，了解边坡在不同时期的变形问题直接关系到整个工程的成败，因此，预测边坡变形问题得到了广大学者的关注。目前国内外常用的预测模型［1］有基于神经网络的预测模型如 BP网络预测，聚类模型和基于时间序列的预测模型，如ARMA模型、ARCH模型。每种模型各有优缺点，也有其适用的范围。灰色系统理论是我国邓聚龙教授［2］于1982年提出来的，是通过生成变换弱化原始序列的随机性，将无规序列生成有规序列，能有效地对生成序列进行预测。而小波分析具有多分辨率的特性，在时频两域都具有表征信号局部特征的能力，是一种很有生命力的信号处理技术，它的一个重要应用即数据去噪，数据去噪能对监测数据进行去噪处理的同时保留真实信号的突变点。

本文将灰色理论和小波理论结合起来对监测边坡位移数据的偶然误差和系统误差进行去噪处理，采用小波－MGM(1，n)［3］预测模型，通过 MatLab 软件对测得的深度位移信号进行分解和重构来模拟真实信号［4］，预测边坡的位移变形，该模型较传统的MGM(1，n)模型预测精度高，可为边坡的治理和防护提供一定的参考依据。

2 时移小波-灰色理论在边坡监测中的应用

2.1 时移小波相关性去噪基本方法

由测斜仪监测的原始位移曲线由于受到自然因素、人为因素等的影响常呈齿状突变分布，需对数据进行去噪预处理来提高MGM(1，n)预测模型的精度。目前常用的经典小波去噪方法有模极大值去噪［5］方法、相关性去噪方法、小波阈值去噪方法。本文采用小波相关性去噪方法，时移小波系数相关性去噪源于空域相关性去噪方法［6］的研究。空域相关性去噪方法针对的是信号序列分解后不同尺度小波系数序列的相关性，而时移小波系数相关性去噪法针对的是不同时间信号序列分解同一层小波系数的相关性。时移小波系数相关去噪先将各时间的信号序列进行小波分解，分解成近似系数和不同尺度小波系数，再算出各尺度小波系数序列的临时同尺度相关系数，利用上述相关性，区别出相关系数很小的噪音所在的尺度，经处理重构后得出近似真实信号。去噪步骤如下:

(1)选定一种小波，对几组相关信号进行小波(小波包)分解，在MatLab中的分解命令为

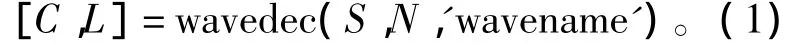
(2)求这几组信号的每个尺度的小波系数两两相关的相关系数。

(3)求各层小波系数邻时的两两相关系数的层相关均值及所有均值的总相关均值。

(4)将层相关均值大于或等于总相关均值的该层小波系数全保持不变。

(5)将层相关均值小于总相关均值的该层小波系数用时间轴上的自相关系数来筛选，将自相关性明显突出的小波系数保留，其他的去除。

(6)将选择置零处理后的小波系数C在MatLab中小波重构，得到去噪后的真实信号，重构命令为

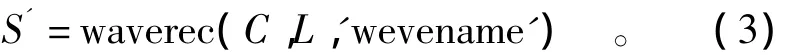
2.2 边坡监测值的小波－MGM(1，n)预测的实现方法

预测模型MGM(1，n)需要的是等间隔的数据序列，而我们所监测的数据一般不是等时间间隔的，因此在利用小波－MGM(1，n)模型时先采用分段线性插值对数据进行预处理，模型预测的实现方法如下［7］:

(1)选择用来信号分解的基本小波类型，运用MatLab中已有的小波分解的命令对深度－位移曲线进行小波分解。

(2)建立MGM(1，n)模型，模型采用生成数列建模，设(t)(i=1，2，3，…，n)为n 个灰时间序列(t)(i=1，2，3，…，n)为相应的一次累加生成序列，即

MGM(1，n)模型的n元一阶常微分方程为

则式(5)可写成矩阵形式，即

则式(6)的连续时间响应式为

为求辨识参数A(v)和B(v)，将式(5)进行离散化得到:

由最小二乘法得到A(v)，B(v)(A(v)，B(v)的最小二乘估计)

式中:L=

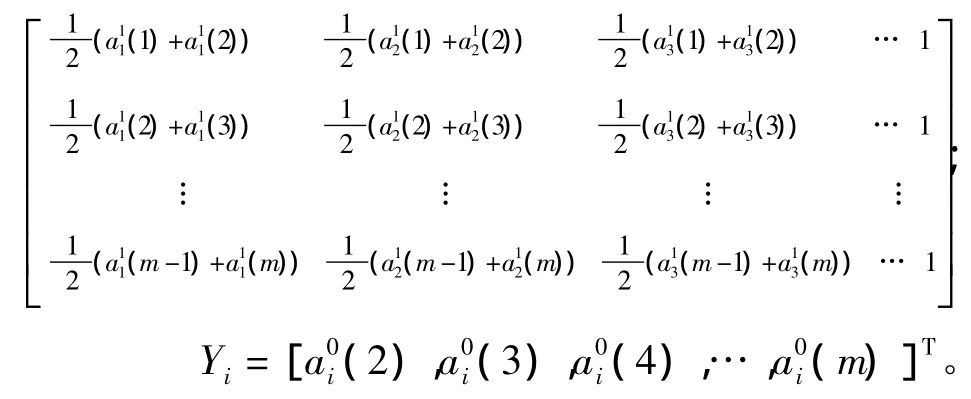
模型MGM( 1，n) 的计算值为

(3)将得到的预测值在MatLab重构，得到生成和预测的深度－位移曲线。

(4)计算预测曲线和实测曲线的残差和自相关系数来校核模型的精度。

3 工程实例

3.1 工程概况

边坡位于锦屏一级水电站坝址区右岸，地势陡峻、基岩裸露、相对高差1 000 m有余，为典型的深切“V”型谷坡，其稳定性对确保施工期和运行阶段的工程安全非常重要。该右岸开挖边坡在2007年布置了3套活动式测斜仪监测边坡内部的位移，本文主要依托该边坡布设在1 885 m高程拌和平台的测斜孔VE01测点当年的累积位移值进行分析研究。本测斜管的监测数据包括A向(左右岸向，向左为正)和B向(上下游向，下游为正)，下文针对B向的系列值来进行处理分析。

图1为2007年6月至10月共9 d的监测数据。高程1 885拌和平台VE01的测值变幅一般都较大，这与该部位岩性及边坡开挖有一定关系。后面的建模分析及预测以这9 d(6月16日至9月4日)的数据为主。表1为这9 d的具体监测数据。

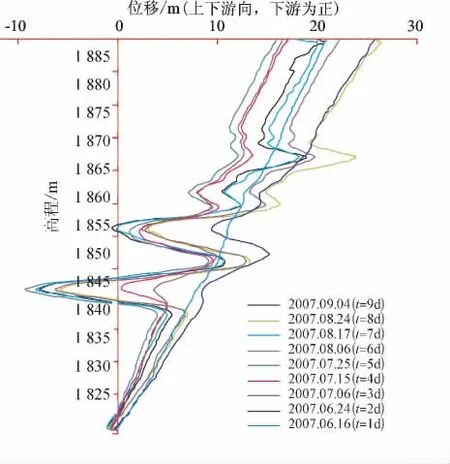
图1 VE01点B向的深度－累积位移Fig.1 Curves of cumulative displacement(in direction B)vs.elevation of point VE01

3.2 监测数据的时移小波处理与灰色模型建模分析

对于该系列累积位移值，首先采用时移小波相关性去噪方法对监测数据降噪处理。由于监测数据的时间间隔不等，因此先对监测数据进行分段线性预插值处理，然后对处理后的数据建立时移小波－MGM(1，n)预测模型进行分析。

为得到更加精确的预测值，本文的灰色预测模型MGM(1，n)采用了2种小波函数(分别为db5，db2)来进行去噪分解处理，这2种小波的分解层数均为6层，各记为db5－6，db2－6，并以此为基础在MatLab中编程实现了这2种小波－MGM(1，n)模型的预测。第1组预测模式db5小波是选取前6天的实测位移数据进行建模，第7天的实测数据用来检验模型的准确性;第2组预测模式db2小波是选取前8天的实测位移数据进行建模，第9天的实测数据用来检验模型的准确性，利用残差自相关系数来校核拟合值和预测值的准确性。

(1)对VE01点B向9天的监测位移数据进行降噪平滑处理后，得到去噪后的深度－累积位移曲线见图2。

(2)对去噪后深度－位移曲线做小波函数为db5的分解层数为6的6－1预测(即6组预测1组)以及预测曲线和实测曲线的残差比较，预测曲线和残差值分别见图3和图4。

表1 VE01点B向累积位移—深度监测数据Table 1 Monitored data of cumulative displacement(in direction B:upstream-downstream direction)vs.elevation of point VE01

图2 VE01点B向去噪前后的深度－累积位移曲线Fig.2 Curves of cumulative displacement(in direction B)vs.elevation of point VE01 before and after de-noising

图3 db5－6分解6－1曲线Fig.3 Six measured curves and one prediction curve with wavelet function db5 and 6 decomposition layers

对该种小波预测模式进行精度检验，其残差自相关系数见表2。

(3)对深度－位移曲线作小波函数为db2的分解层数为6的8－1预测(即8组预测1组)以及预测曲线和实测曲线的残差比较，预测曲线和残差值结果分别见图5和图6。

对该种小波预测模式进行精度检验，其残差自相关系数见表3。

图4 db5－6分解6－1残差Fig.4 Residuals of six measured curves and one prediction curve with wavelet function db5 and 6 decomposition layers

图5 db2－6分解8－1曲线Fig.5 Eight measured curves and one prediction curve with wavelet function db2 and 6 decomposition layers

通过对小波函数为db5和db2的分解和重构和比较残差和残差自相关系数，发现时移小波－灰色理论能够很好地模拟真实信号并预测出深度－位移曲线，用小波函数db2作6层分解的(8组预测1组)模式的效果不及用小波函数db5作6层分解的(6组预测1组)模式。当然并不局限于这2种模式，可以通过改变小波函数、分解层次和基础数据组数来寻求最佳的预测模式。

图6 db2－6分解8－1残差Fig.6 Residuals of eight measured curves and one prediction curve with wavelet function db2 and 6 decomposition layers

表2 db5－6－1小波预测的残差自相关系数Table 2 Residual autocorrelation coefficient of db5 wavelet prediction

表3 db2－8－1小波预测的残差自相关系数Table 3 Residual autocorrelation coefficient of db2 wavelet prediction

4 结论

本文基于时移小波－灰色理论基础，利用Mat-Lab的软件包工具箱，对测得的深度位移曲线进行去噪处理并将时移小波进行分解与重构，得到如下结论:

(1)时移小波系数相关性去噪，利用了不同时间的白噪音的不相关性和真实信号的相关性，能较好地对监测数据进行降噪平滑处理。

(2)小波－MGM(1，n)预测模型利用n组相关联的数据来预测下一阶段的数据的精度较高，该方法可以任意选择Daubechies(db N)小波系列中的函数类型、分解层数、起始曲线以及基础数据组数，可以作出几组预测，比较残差后，选择最佳预测曲线。

［1］王 波.一种改进的灰色预测模型分析［J］.太原城市职业技术学院院报，2012，(6):166－167.(WANG Bo.An Improved Grey Prediction Model Analysis［J］.Journal of Taiyuan Urban Vocational College，2012，(6):166－167.(in Chinese))

［2］邓聚龙.灰色系统基本方法［M］.武汉:华中理工大学出版社，1987.(DENG Ju-long.Grey System Method［M］.Wuhan:Huazhong University of Science and Technology Press，1987.(in Chinese))

［3］毛亚纯，贾崴崴，沙成满，等.基于小波分析的灰色预测法预测边坡变形［J］.矿业工程，2010，8(6):17－20(MAO Ya-chun，JIA Wei-wei，SHA Cheng-man，et al.Wavelet Analysis Based Grey Model Applied in Prediction of Slope Deformation［J］.Journal of Mining Engineering，2010，8(6):17－20.(in Chinese))

［4］吴 伟，蔡培升.基于Matlab的小波去噪仿真［J］.信息与电子工程，2008，6(3):202－ 222，229.(WU wei，CAI Pei-sheng.Simulation of Wavelet Denoising Based on MatLab［J］.Information and Electronic Engineering，2008，6(3):220－222，229.(in Chinese))

［5］MALLAT S，HWANG W L.Singularity Detection and Processing with Wavelets［J］.IEEE Transactions on Information Theory，1992，38(2):617－643.

［6］XU Y S，WEAVER J B，HEALY D M，et al.Wavelet Transform Domain Filters:A Spatially Selective Noise Filtration Technique［J］.IEEE Transactions on Image Processing，1994，3(6):747－758.

［7］徐建江，裴 亮.基于小波分析的MGM(1，N)模型在大坝监测系统中的应用［J］.中国农村水利水电，2013，3(7):108－ 110，117.(XU Jian-jiang，PEI Liang.The Application of Dan Monitoring Systems Based on MGM(1，N)Model on Wavelet Analysis［J］.Journal of China Rural Water and Hydropower，2013，3(7):108－110，117.(in Chinese))