基于Q系统与数值模拟的地下岩洞锚喷支护参数研究

曹洋兵，晏鄂川，徐 军，张婷婷

(1.中国地质大学(武汉)工程学院，武汉 430074;2.北京东方新星石化工程股份有限公司，北京 100070)

1 研究背景

目前，对于地下工程围岩稳定性和支护安全性缺乏通用的评价指标，工程类比和工程经验在围岩支护决策中起着非常重要的作用。如何科学、合理地确定地下岩石洞室锚喷支护参数具有十分重要的理论与工程意义。

在连续介质力学的框架内，将围岩看作弹塑性或黏弹塑性体，在确定围岩压力的基础上采用结构力学计算锚喷支护参数是目前主要的求解思路。郑颖人等［1－2］分别采用弹塑性力学和黏弹塑性力学得出了确定锚喷支护参数的计算式;董方庭等［3］提出了围岩松动圈支护理论。基于数值模拟技术，Hoek等［4］提出支护性能图的方法进行支护设计;朱万成等［5］采用回归正交试验确定锚喷参数;郑颖人等［6］应用强度折减法求解围岩稳定系数，并在此基础上研究了锚喷设计。

考虑到围岩力学性状的不确定性与时空变异性，徐军等［7］基于可靠性理论与概率极限状态设计法研究了锚喷支护结构的可靠性，并且工程类比模糊经验法［8］、专家系统［9］、BP 神经网络［10］及人工智能综合集成的动态设计法［11］也都应用到锚喷支护设计中，有力地推动了锚喷设计理论的发展。同时，由于地下工程建设特点，基于围岩分类的支护设计方法受到重视并不断发展，如 Q系统［12－13］、RMR 法［14］和 RMi法［15］等。冯夏庭等［16］将岩石工程设计方法分为1∶1映射和非1∶1映射2大类，并指出综合多种方法进行设计的重要性。

本文采用GSI和Hoek-Brown准则架起Q系统与数值模拟的桥梁，首先采用Q系统确定围岩锚喷支护参数，再采用离散单元法(3DEC)分别从连续围岩和考虑优势结构面随机组合的非连续围岩2种角度对Q系统得出的锚喷参数进行检验，最后结合校验结果进行了相关讨论。

2 研究区概况与地应力分布特征

2.1 研究区工程概况

山东某地下水封液化石油气岩石洞库处于华北断块区东部的胶辽断块中，建库区岩石介质为燕山早期中粗粒黑云二长花岗岩，按储存介质分为3个洞罐，见图1。初步设计出的地下工程主要包括9个主洞室、4个竖井、9个封塞、10条主水幕巷道和1条主施工巷道。

图1 主要地下工程平面布置Fig.1 Layout of main underground facilities

基于地表半迹长测线法测量结果，得出花岗岩体内结构面优势产状为:NE54°～84°∠79°～89°，SE105°～138°∠78°～84°，SW234°～257°∠83°～89°，NW285°～309°∠66°～88°。通过钻孔摄像技术发现一组优势产状为NW309°～339°∠16°～22°的缓倾角结构面。现场调查发现，花岗岩体结构面的类型主要为节理，基本无充填(极少数有薄层泥质充填)，表面形态为粗糙～平滑(小尺度)和平坦状～波状(中等尺度)。

2.2 场区地应力分布特征

洞库场地处于丘陵与冲洪积平原过渡地带，地面高程22.0～35.0 m，平均高程 30 m，总体坡度小于5°，以下假定地面标高统一为30 m。经张量统计与线性回归分析，可得式(1)，其中拉应力为正、压应力为负，垂直地应力为最小主应力。

式中:σH为最大主应力值(MPa);σh为中间主应力值(MPa);σv为最小主应力值(MPa);h为高程(m)。岩体重度取27 kN/m3。

3 基于Q系统的洞室锚喷支护设计

选择洞罐A(图1)作为支护设计的研究对象，该洞罐的主洞室截面形状为曲墙圆拱，洞高26 m，跨度22 m，主洞室拱顶标高－120 m，轴向东西向。针对Q=4的洞库围岩段，按以下步骤进行洞室支护设计。

(1)按照文献［12］的 ESR(Excavation Support Ratio)建议取值表，并根据液化石油气地下工程的重要性与使用年限，综合确定ESR为1.0。因而，洞室的设计跨度和高度仍分别为22 m和26 m。

(2)根据式(2)［12］，可得洞顶岩体质量 Qroof=4，洞边墙岩体质量Qwall=10。

(3)通过Q系统围岩支护图［13］，可得初步锚喷支护参数:拱顶为长5.5 m、间距2.1 m 的锚杆，厚度8 cm的喷射钢纤维混凝土;边墙为长6 m、间距2.3 m的锚杆，厚度6 cm的喷射钢纤维混凝土。从方便施工与安全角度对以上参数进行优化，确定拱顶和边墙统一采用长6 m、环向和纵向间距都为2 m的锚杆，厚度为8 cm的喷射钢纤维混凝土。

(4)采用式(3)［12］确定支护压力 P。

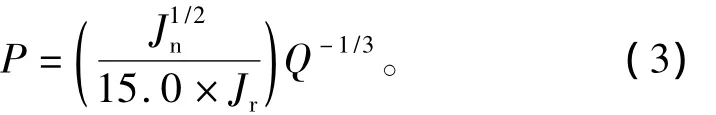
式中:Jr为节理粗糙度，Jn为节理组数，其值可通过Q分类参数表确定。

根据场地结构面调查情况和工程经验，取“2组结构面+随机结构面”(Jn为6)与“3组结构面”的Jn平均值进行设计，即Jn取7.5。研究区结构面的表面形态主要为粗糙～平滑(小尺度)和平坦状～波状(中等尺度)，本次取“粗糙+平坦状”(Jr为1.5)与“平滑 +平坦状”(Jr为1.0)的 Jr平均值进行设计，即 Jr取1.25。由此可得:拱顶支护压力Proof为0.092 MPa，边墙支护压力 Pwall为0.068 MPa。

(5)规定采用牌号HRB400、直径25 mm的锚杆，灌注M30的水泥砂浆。则每根锚杆抗拉力设计值为176 kN，支撑的面积:对于 Proof为0.092 MPa，为1.92 m2;对 Pwall为0.068 MPa，为2.61 m2。规定采用CF35的钢纤维混凝土，在考虑其支护效果的基础上，初步认为每根锚杆能支承的面积都为2.0 m2。由此得以下锚杆布置:环向间距2 m，纵向间距1 m，梅花形布置。底板设计可参考Nick Barton的建议或相关规范，本次采用厚15 cm的C25混凝土。

需要注意的是，Q系统围岩支护图中所提出的锚杆间距参数，是基于屈服强度为500 MPa的锚杆。这是后续通过支护压力进行详细设计，并对锚杆的初始间距进行了明显调整的重要原因。

4 基于数值模拟的锚喷参数校核

Q系统本质上是一种类比设计方法。因而，采用数值模拟这种更为客观的支护设计方法对Q系统得出的锚喷参数进行校核具有十分重要的意义。

4.1 数值模拟概况

采用3DEC离散元软件，按右手空间直角坐标系，洞室轴向沿y轴建立，长度为6 m，高程增大的方向为z轴正向，模型边界取大于3倍的洞跨和洞高的位置。洞室周边1倍洞跨和洞高范围网格尺寸为1.5 m，外围取4.0 m，都为常应变四面体单元。

基于数值模型方位与洞室真实方位的关系，将地应力按张量原则转换得到数值模型边界的应力，并作为相应的应力边界条件。模拟中的开挖方案与实际相同，即分4层开挖，第1层开挖完后再挖第2层，并以此类推。数值模拟中各台阶每次开挖进尺为1 m，锚杆采用cable单元，钢纤维混凝土采用liner单元。

4.2 岩体、结构面与支护结构的模拟参数

由于现有数值计算技术尚难以考虑结构面复杂的空间几何形态，因而无法建立与Q系统各参数完全对应的岩体三维数值模型。本文通过 GSI和Hoek-Brown准则建立起Q值与岩体等效力学参数间的关系。在假定Q分类中Jw和SRF都为1的前提下，GSI和 Q 值具有式(4)［17］的关系，即

式(4)中采用Q'而不是Q值的原因在于防止水和地应力等作用被重复考虑，由于本文不考虑水岩耦合作用，因而需将岩体力学参数进行一定的折减。对于本文实例，SRF取1，因而考虑水效应的Q'与Q值等同，为4，则GSI为56.5。通过室内试验得出岩石单轴抗压强度为65 MPa，密度2 700 kg/m3;基于岩性mi取值表，得中粗粒花岗岩mi为30;考虑一定的爆破损伤效应，损伤度D取0.2;洞库埋深范围最大水平地应力为10.5 MPa。模拟中岩体采用摩尔－库伦本构模型，基于2002版 Hoek-Brown准则［18］估算出岩体力学参数，其中抗拉强度结合试验成果进行综合确定，详见表1。

表1 岩体力学参数Table 1 Mechanical parameters of rock mass

结构面采用摩尔－库伦滑动本构模型，其强度参数基于室内试验结果，法向刚度和切向刚度依经验取值，见表2。

表2 结构面力学参数Table 2 Mechanical parameters of discontinuity

基于Q系统得出的锚杆设计参数(表3)，锚杆孔内砂浆体黏结强度和黏结刚度采用Christopher等［19］提出的估算公式，即

式中:Kbond为黏结刚度;G为砂浆剪切模量(1010Pa);t为砂浆圆环厚度(37.5 mm);D为锚杆直径(25 mm);Sbond为砂浆黏结强度;τpeak为砂浆峰值剪切强度;τ1取围岩和砂浆单轴抗压强度较小者的1/2(6 MPa);QB为砂浆与围岩黏结质量(0～1范围内，黏结质量最好时为1)，取0.4。得出的砂浆参数见表3。

表3 锚杆单元模拟参数Table 3 Simulation parameters of rockbolt element

模拟CF35钢纤维混凝土喷层的Liner单元在3DEC中被离散为三角形弹性板，其厚度为8 cm，其余参数参考相关规范与工程经验，见表4。

表4 喷层单元模拟参数Table 4 Simulation parameters of liner element

4.3 连续围岩条件下的锚喷参数校核

由图2可知，洞室开挖完成后，其二次应力总体分布特征为:洞室周边径向应力基本为0，局部出现了较小的拉应力(约49 kPa);拱顶与边墙两脚点处(边墙与底板交接处)呈现出明显的切向压应力集中，最大值为25.33 MPa，此值约为原岩应力的2.4倍。

计算过程中，各监测点位移随时步的变化曲线见图3。由图3可知，每次开挖后监测点位移会出现跃升(0.5 mm左右)，随着支护的施加，其位移有明显的收敛现象，最终的最大位移为1.4 cm左右，且在第2～4层开挖时，拱顶位移有逐渐减小的现象，其最终减小值为1.5 mm左右。上述结果说明，支护对于围岩变形具有明显的控制作用，证实了支护结构的有效性。

基于数值极限分析法［20］，采用超载安全系数对支护结构的安全性进行评价。由图4(a)可知，锚杆所受的拉力基本在25～50 kN范围内，最大拉力为71.2 kN。由于单根锚杆的极限抗拉力为196 kN，则计算结果表明锚杆处于安全状态，最小安全系数为2.75。对于CF35喷射钢纤维混凝土，其抗压强度为23.4 MPa，抗拉强度为4.2 MPa，通过计算发现，控制其破坏的主要是抗拉强度。由图4(b)可知，喷层的较大拉张应力(拉力为负号，即为最小薄膜应力)位于边墙中部及与底板交接处，最大值为3.37 MPa，则喷层的安全系数为1.25。

图2 开挖完成后洞室二次应力张量Fig.2 Secondary stress tensor of cavern after finishing excavation

图3 洞周监测点位移－时步曲线Fig.3 Relationship between displacement of cavern peripheral monitoring point and time-step

图4 连续围岩条件下的支护受力Fig.4 Support force in the presence of continuous surrounding rock

综上可知，在连续围岩条件下，基于Q系统所得出的支护参数对围岩位移的控制作用明显，支护结构的安全系数在合理范围内，表明支护参数是有效和安全的。

4.4 优势结构面随机组合情况的锚喷参数校核

基于研究区发育的5组优势结构面，按位置随机的方式加入数值模型中，其中结构面间距设置较大(20 m)，使其在洞室及周边呈现随机稀疏分布，以保证取岩体等效力学参数的合理性。

由图5可知，由于结构面的不利组合，洞室右边墙出现了2处失稳块体，其体积均较小，不超过3 m3。由钢纤维混凝土喷层受力(图6(a))可知，喷层在2块体失稳处均出现了很大的拉张应力，其最大值达35.3 MPa，远大于喷层的弯拉强度，其中靠近洞肩处的失稳块体在喷层中产生的拉张应力较下处大。同时，由锚杆轴力(图6(b))分布情况可知，在2块体失稳处的锚杆最外段的轴力都达到了极限强度。由此可知，在该种岩体结构状况下，由于局部块体失稳导致支护结构发生了破坏，表明锚喷支护参数是不安全的。

图5 围岩位移云图及失稳块体位置Fig.5 Displacement of surrounding rock and position of instability block

图6 优势结构面随机组合情况下的支护受力Fig.6 Support force in the presence of random combination of main discontinuities

4.5 讨 论

地下岩石洞室在工程开挖作用下，迅速地形成二次应力场，并在围岩中呈现多种圈层(破坏圈、损伤圈和弹性扰动圈)耦合的变形破坏特征。科学、合理的锚喷支护设计理论应该是基于围岩的变形破坏模式及其发生条件和机制之上，真正做到“对症下药”。通过本文数值模拟验证结果可知，Q系统对于局部随机块体失稳这种变形破坏模式是不适用的。其原因在于围岩的局部结构失稳问题随机性大、个性明显，难以在施工前进行准确的判定和评价，也难以给出普适性的锚喷支护参数。

从统计类比上看，Q系统最初是基于200多个工程实例统计得来，后又依据1 050个实例对SRF取值(考虑断层、强度应力比、挤出和膨胀的影响)和支护类型(采用钢纤维混凝土)等进行过修正的设计方法，那么其适用范围就应被限定在与其基于的工程实例较为类似的地下工程之中。这说明在进行Q系统的工程应用时，有必要结合数值模拟进行锚喷参数的校核和优化。另对于块体掉落、滑落等局部失稳问题，受结构面空间组合关系及其力学特性控制，一般在洞室周边的特定部位产生，并在二次应力重分布过程中受到抑制或加剧，采用考虑结构面的离散单元法可合理地对此进行稳定性分析和支护安全性计算。这是数值模拟除了对Q系统设计的锚喷参数进行校核和优化外，应着重关注的问题，以最终达到Q系统与数值模拟的取长补短，相互校核和合理优化。

5 结论

本文基于地应力与结构面分布特征，应用Q系统对地下岩洞进行锚喷支护设计，并结合离散元数值模拟进行检验研究，得出以下主要结论:

(1)本文采用 GSI和Hoek-Brown准则建立Q值与岩体等效力学参数的关系，并基于此采用数值模拟对Q系统设计出的锚喷参数进行校核，以确定最终的支护参数的思路是合理、可靠的，可为相关地下岩石工程提供参考。

(2)连续围岩条件下的数值模拟表明，基于Q系统的锚喷支护参数是有效和安全的，表现在支护对围岩变形的控制作用明显，锚杆的最小安全系数为2.75，钢纤维混凝土喷层的安全系数为1.25，安全系数在基本合理范围内。

(3)基于Q系统所得的锚喷支护参数不针对局部块体失稳问题，因而需结合离散元数值模拟等进行综合设计，并且在施工期要特别重视对可能发生的局部失稳问题进行提前甄别。

(4)本文研究主要针对施工前的预设计，采用的计算参数、结构面组合状况等具有很大的经验性和不确定性。随着工程建设的进行，根据施工期地质、监测和现场测试等资料对模拟参数进行调整或反分析、动态识别局部块体失稳、评价和优化锚喷支护方案等内容的研究是后续需要进行的。

［1］郑颖人，刘怀恒，顾金才.均质地层中锚喷支护理论与设计［J］.岩土工程学报，1981，3(1):57－69.(ZHENG Ying-ren，LIU Huai-heng，GU Jin-cai.Theory and Design of Shotcrete Lining and Rock Anchorage in Homogeneous Strata［J］.Chinese Journal of Geotechnical Engineering，1981，3(1):57－69.(in Chinese))

［2］郑颖人，刘怀恒.隧洞黏弹塑分析及其在锚喷支护中的应用［J］.土木工程学报，1982，15(4):73－78.(ZHENG Ying-ren，LIU Huai-heng.Viscoelastic-plastic Analysis of Tunnels and Its Application to Anchoring and Shotcrete Lining［J］.China Civil Engineering Journal，1982，15(4):73－78.(in Chinese))

［3］董方庭，宋宏伟，郭志宏，等.巷道围岩松动圈支护理论［J］.煤炭学报，1994，19(1):21－32.(DONG Fang-ting，SONG Hong-wei，GUO Zhi-hong，et al.Roadway Support Theory based on Broken Rock Zone［J］.Journal of China Coal Society，1994，19(1):21－32.(in Chinese))

［4］HOEK E，CARRANZA-TORRESC，DIEDERICHSM S，et al.Integration of Geotechnical and Structural Design in Tunnelling［C］//Proceedings University of Minnesota 56th Annual Geotechnical Engineering Conference.New Jersey:Wiley，2008:1－53.

［5］朱万成，赵 文，唐春安，等.锚喷参数的回归正交有限元试验分析及其应用实例［J］.岩石力学与工程学报，1999，18(3):283－ 286.(ZHU Wan-cheng，ZHAO Wen，TANG Chun-an，et al.Regressive Orthogonal FEM Experimental Analysis of Bolt-spray Parameters and Its Application［J］.Chinese Journal of Rock Mechanics and Engineering，1999，18(3):283－286.(in Chinese))

［6］郑颖人，邱陈瑜，宋雅坤，等.土质隧道围岩稳定性分析与设计计算方法探讨［J］.后勤工程学院学报，2009，25(3):1－ 9.(ZHENG Ying-ren，QIU Chen-yu，SONGYa-kun，et al.Exploration of Stability Analysis and Design Calculation Methods of Surrounding Rocks in Soil Tunnel［J］.Journal of Logistical Engineering University，2009，25(3):1－9.(in Chinese))

［7］徐 军，郑颖人，刘东升.锚喷支护喷层结构的目标可靠指标和分项系数研究［J］.岩石力学与工程学报，2002，21(5):671－ 674.(XU Jun，ZHENG Ying-ren，LIU Dong-sheng.Research on Object Reliability Index and Partial Coefficient of Bolt-shotcrete Lining for Tunnel［J］.Chinese Journal of Rock Mechanics and Engineering，2002，21(5):671－674.(in Chinese))

［8］朱琢华，黄宏伟，杨新安.锚喷支护设计的工程类比模糊经验法［J］.煤炭学报，1998，23(6):571－574.(ZHU Zhuo-hua，HUANG Hong-wei，YANG Xin-an.The Engineering Analogy Fuzzy Experiential Method for Design of Rockbolt and Shotcrete Support［J］.Journal of China Coal Society，1998，23(6):571－ 574.(in Chinese))

［9］冯夏庭，林韵梅.采矿巷道围岩支护设计专家系统［J］.岩石力学与工程学报，1992，11(3):243－253.(FENG Xia-ting，LIN Yun-mei.An Expert System for the Design of Surrounding Rock Support System in Mine Entries［J］.Chinese Journal of Rock Mechanics and Engineering，1992，11(3):243－253.(in Chinese))

［10］汤劲松，乔春生.隧道锚喷支护设计的神经元网络方法［J］.中国公路学报，2002，15(3):68－72.(TANG Jin-song，QIAO Chun-sheng.Method of Artificial Neural Network for Bolt-shotcrete Support Design in Tunnels［J］.China Journal of Highway and Transport，2002，15(3):68－72.(in Chinese))

［11］冯夏庭，江 权，向天兵，等.大型洞室群智能动态设计方法及其实践［J］.岩石力学与工程学报，2011，30(3):433－448.(FENG Xia-ting，JIANG Quan，XIANG Tianbing，et al.Intelligent and Dynamic Design Method of Large Cavern Group and Its Practice［J］.Chinese Journal of Rock Mechanics and Engineering，2011，30(3):433－448.(in Chinese))

［12］BARTON N，LIEN R，LUNDE J.Engineering Classification of Rock Mass for the Design of Tunnel Support［J］.Rock Mechanics，1974，6(4):189－236.

［13］GRIMSTAD E，BARTON N.Updating of the Q-system for NMT［C］//Proceedings of the International Symposium on Sprayed Concrete-Modern Use of Wet Mix Sprayed Concrete for Underground Support.Norway:Fagernes，October 18－21，1993:1－21.

［14］BIENIAWSKI Z T.Engineering Rock Mass Classifications［M］.New York:John Wiley and Sons，1989.

［15］PALMSTRON A.Characterizing Rock Masses by the RMi for Use in Practical Rock Engineering，Part 1:the Development of the Rock Mass Index(RMi)［J］.Tunneling and Underground Space Technology，1996，11(2):175－188.

［16］FENGX T，HUDSON JA.The Ways Ahead for Rock Engineering Design Methodologies［J］.International Journal of Rock Mechanics and Mining Sciences，2004，41:255－273.

［17］HOEK E，KAISER P K，BAWDEN W F.Support of Underground Excavations in Hard Rock［M］.London:Taylor ＆ Francis，1995.

［18］HOEK E，CARRANZA-TORRES C，CORKUM B.Hoek-Brown Criterion—2002 Edition［C］//Proceedings of North American Rock Mechanics Society Meeting in Toronto，July 8－10，2002:267－273.

［19］CHRISTOPHER M，JOHN S，DAVID E，et al.Rockbolts:A New Numerical Representation and Its Application in Tunnel Design［C］//Proceedings of the 24th U.S.Symposium on Rock Mechanics.New York:Association of Engineering Geologists，June 20－23，1983:13－25.

［20］郑颖人.岩土数值极限分析方法的发展与应用［J］.岩石力学与工程学报，2012，31(7):1297－1316.(ZHENG Ying-ren.Development and Application of Numerical Limit Analysis for Geological Materials［J］.Chinese Journal of Rock Mechanics and Engineering，2012，31(7):1297－1316.(in Chinese))