弱链对角占优M－矩阵最小特征值的下界研究

李艳艳，蒋建新 （文山学院数学学院，云南 文山663000）

弱链对角占优矩阵在科学研究中有着广泛的应用，可以用于大规模数字电路的设计，解决大型线性方程组中的矩阵分裂，证明矩阵分裂迭代方法的收敛性等问题。对于弱链对角占优矩阵的研究，自从1996年P.N.Shivakumar给出一些经典结果以来，关于它的研究一直就没有间断过，并得到了许多有价值的结果。

1 基本概念

设Cn×n（Rn×n）表示n×n复（实）矩阵的集合，N＝ ｛1，2，…，n｝；A＝（aij）∈Rn×n表示n阶实方阵；Ri；J（A）＝ ｛i∈N：di＜1｝；sji＝i，i，j∈ N；，j≠i，j∈N；pi＝∈N。

定义1 集合Zn×n＝ ｛A＝（aij）｜A∈Rn×n，aij≤0，∀i，j∈N，i≠j｝中的矩阵称为Z－ 矩阵；若A为Z－矩阵且A－1≥0（A－1为非负矩阵），则称A为非奇异M－矩阵。

定义2 设A＝（aij）∈Rn×n，若di≤1，J（A）≠，且对iJ（A），必存在非零元素链，其中i1≠i≠i2，…，ir≠ik，0≤r≤k－1，ik∈J（A），则称A为弱链对角占优矩阵（WCDD）。

定义3 若将矩阵A＝（aij）∈Cn×n分裂为A＝D－C（D为A的对角矩阵，即D＝diag（a11，a22，…，ann），则矩阵JA＝D－1C称为A的迭代矩阵。

文献［1］给出了关于弱链对角占优矩阵A＝（aij）∈Rn×n的逆矩阵A－1＝（αi）j元素的估计式：

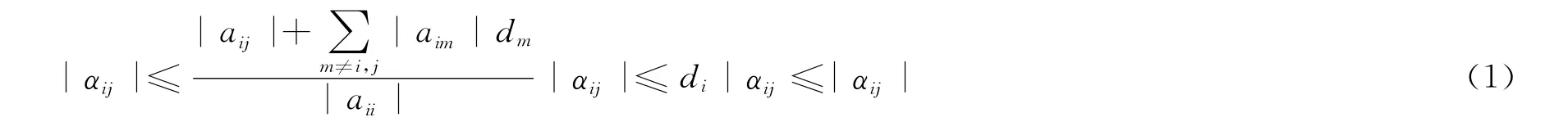
且对任意的i∈N，有：

下面，笔者借助弱链对角占优M－矩阵A的逆矩阵A－1的非主对角元素上界估计式给出了主对角元素新的估计式，从而与该类矩阵的最小特征值τ（A）经典的下界估计式结合得到新的提高的且易于计算的界。

2 主要结果

定理1 设A＝（aij）∈Rn×n是弱链对角占优的M－ 矩阵，A－1＝（αij），则：

且对任意的i∈N，有：

证明 因为A是M－矩阵，所以αij≥0，即：

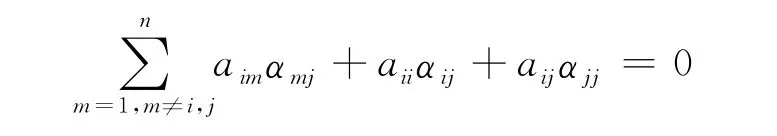
也即：

两边取绝对值应用式（1）得：

又由定理1的条件去掉绝对值得｜αjj｜≤－，即式（3）得证。

由AA－1＝I，有＝1，则应用式（3）有：

则：

即：

则式（4）的右边得证。左边的证明类似。

引理1［2］设M＝（βij）是非奇异的M－ 矩阵，N＝（γij）是与M具有相同阶数的非负矩阵，N＝M－A，M－1N＝JA，则：

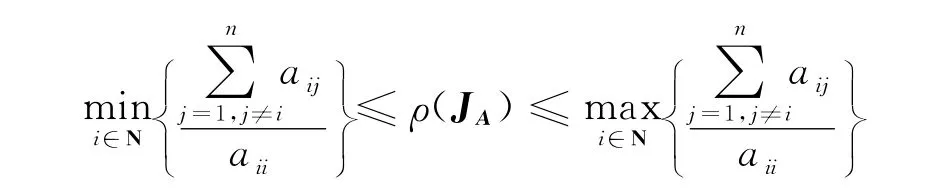
引理2［2］设A＝（aij）是非奇异的M－ 矩阵，A－1＝（αij），则：

式中，ρ（JA）是A的Jacobi迭代矩阵JA的谱半径。

定理2 设A＝（aij）∈Rn×n是弱链对角占优的M－矩阵，则：

证明 因为A是弱链对角占优的M－矩阵，应用定理1得：

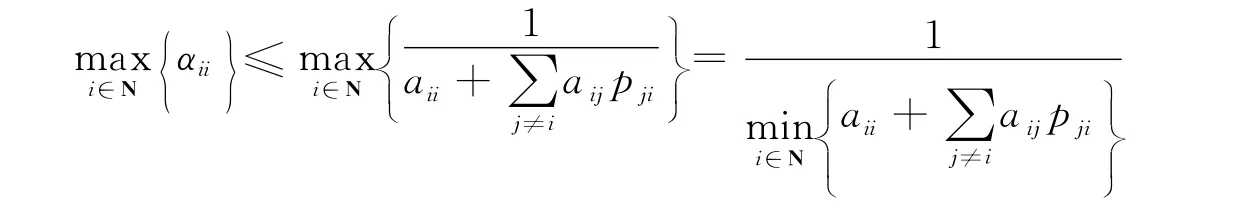
所以：

又由引理1知ρ（JA）则：

将式（7）与式（8）代入引理2中的不等式（5）得式（6）。

式（5）中的ρ（JA）当矩阵的阶数较大时，很难计算，所以引理2的实际价值并不是太高，可是定理2中的估计式（6）只涉及矩阵A的元素，所以比式（5）更加容易计算。

3 数值算例

设A容易验证A是弱链对角占优的M－矩阵，应用定理2知τ（A）≥0.8723；但是应用引理2得到τ（A）≥0.4569，事实上τ（A）＝1.0424。

该算例进一步说明了定理2提高了引理2的结果，并且新的估计式只与矩阵的元素有关，因而更容易计算。

［1］Li Houbiao，Huang Tingzhu，Li Hong.Lower bounds for the eigenvalue of Hadamard product of an M－matrix and its inverse ［J］.Linear Algebra Appl，2007，420：235～247.

［2］Tian Guixian，Huang Tingzhu.Inequalities for the minimum eigenvalue of M－matrices ［J］.Electronic Journal of Linear Algebra，2010，78：291～302.