三维地质模型的一种快速建模方法研究

陈续威，谢凯，刘波，张圳，白志君 长江大学电子信息学院

长江大学油气信息处理与识别研究所，湖北 荆州434023

随着复杂几何模型建模的需求日益增加，快速建模技术也应运而生。在计算机图形学领域，经常采用多边形网格来描述物体的几何模型。对于小数据量的地质模型，采用一般的建模技术足以满足要求，但是对于复杂不规则的地质模型（如包含断层、褶曲、开挖边界等），其网格通常由成千上万个多边形面片组成［1，2］。由于将多边形映射为图像的过程需要进行大量计算，因而花费的绘制时间相当长，存储量也特别大。随着地质学研究的深入，数据量庞大的复杂地质模型通常不能满足实时绘制的需要。为此，笔者对三维地质模型的一种快速建模方法进行了研究，以便能够在保持较高逼真度的前提下实现运算速度的大幅提升以及模型的大幅度简化，从而满足实时绘制的需要。

1 建模原理与流程

三维地质模型的快速建模方法的基本原理是通过删除一部分在精度范围内的顶点，即减少运算数据的方式，从而达到加快建模速度的目的［3，4］。三维地质模型的快速建模方法流程图如图1所示。

2 建模过程

2.1 计算法矢量

读取文件中的地质网格数据，将地质数据进行三角形细分后，任取一个交点，计算出周围所有三角形的法矢量，求出平均值，作为该点的法矢量，并进行归一化处理。依此类推，可以计算出所有网格点的单位法矢量。

对于复杂地质体的网格模型，为了提高其建模的精确度，采用6个点（其中有2个重点）画2个三角形的方式进行三角形细分（见图2），可得到三角形面的个数为2＊（columns＊rows），对得到的三角形面片，根据其3个顶点可以唯一确定该三角面片的法矢量，具体方法如下［5］。

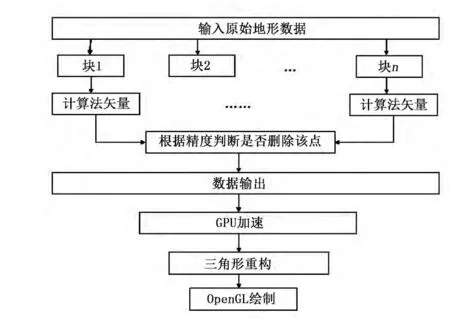
图1 三维地质模型的快速建模方法流程图

设三角形的3个点分别为A、B、C（逆时针排列），其法矢量为→h，则：

三角形细分后，对网格面中的任意一个交点q，其周围将存在n个（此处n＝6）三角形（见图2）。

设第i个三角形的单位法矢量为（i＝1，2，…，n），则交点q的法矢量可用其周围所有（此处为6个）三角形面的法矢量的平均值来表示，若表示交点q的法矢量，则：

图2 模型网格面及其三角形细分

由于的模值分布区间较大，不易后续处理，现对其进行归一化（即取模为1），设归一化后的单位法矢量为，则：

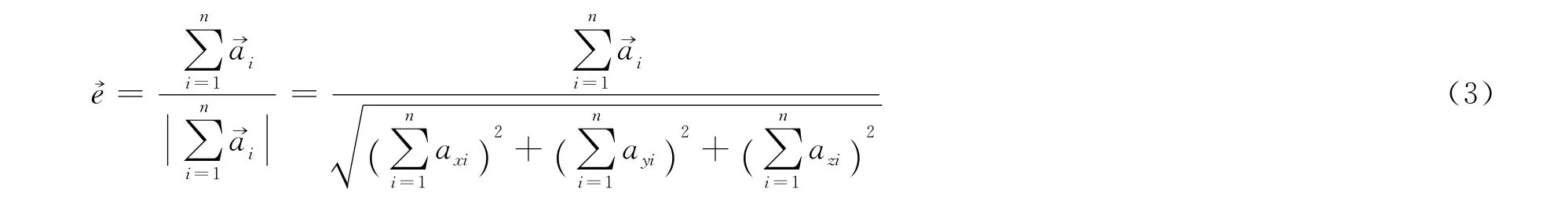
式（3）即为平均后的单位法矢量，现将其定义为复杂地质网格面交点q的单位法矢量。

2.2 修正法矢量

某一点修正后的法矢量是由周围所有网格交点的单位法矢量所共同决定的，算出其平均值，即为该点修正后的法矢量。为了提高复杂地质模型处理后的逼真度，根据某一网格点周围所有点的单位法矢量，求出其平均值作为该点修正后的法矢量。点q修正后的单位法矢量是周围所有点单位法矢量的平均值（见图3），由此可以算出周围8个点，，…，的单位法矢量。修正后的法矢量用表示，即：

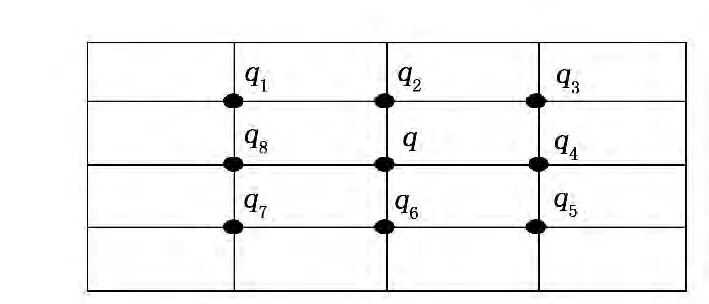
图3 网格交点及其法矢量平均

2.3 数据简化

模型简化算法是在给定精度ε的条件下，求出某一网格点与周围点修正后的法矢量的夹角θ，将求得的夹角θ换算成弧度值后与设定的精度值ε进行比较，由此决定是否删除该网格点。

在一定的精度范围ε内，利用模型简化算法对所有点进行有选择性的删除。从视觉效果看，当多个点的法向量的方向近似相同时，它们所构成的曲面近似平缓，此时在一定精度范围内，部分数据是不必要的（见图4）。在这种情况下，可以删除不必要的数据，从而实现地质模型的快速建模。设置绘制精度为ε，周围点的修正法矢量为（i＝1，2，…，8），计算出某一网格点 （非边界点）与周围点的修正法向量所组成的夹角θi：

图4 曲面的一维数学模型图

设：

当δi（i＝1，2，…，8）小于绘制精度ε时，表明周围的点与该网格点的修正法矢量相差不大，即周围8个点对该点的影响是可以接受的，此时可以删除该网格点。由于反余弦函数在 ［－1，1］区间内呈单调递减，故可将表达式：

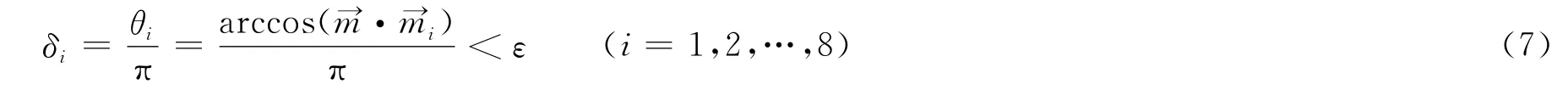
转化为：

令N＝cos（επ），则：

当δi（i＝1，2，…，8）不全小于绘制精度ε时，则表明周围的点中存在与该网格点的修正法矢量相差较大的点，此时将保留该网格点。此外，边界点将全部保留。

2.4 数据重构

对处理后的数据进行三角形网格重构，采用改进后的分治算法，生成三角网。在重构过程中，首先利用八叉树算法［6］对已筛选过的地质数据进行分块处理和存储，若某块内的数据是不匀质的，则再次进行八叉树划分，块内的地质数据匀质时则不必再次分块。然后，将分块后的数据放到GPU线程块中，再将非匀质块细分给每个块内线程，利用GPU同一线程块的线程可以相互通信的优势，让指向各个不同地质信息数据的指针能够在线程间并行移动，由此防止指针出现混乱。此外，每个线程块还要进行同步处理，保证每个线程都能完成其相应的计算。

3 试验结果与分析

采用某地区的地质体数据进行试验以检验上述方法。该模型为985×748的网格数据，原始网格点数目为736780。对模型数据进行了3次简化，然后计算了简化比、平均交互速度和对称Hausdorff距离（见表1）。分析表1数据可知，随着顶点数的减少，三角形面片数也减少，简化比增加，平均交互速度增加，这说明建模速度加快。采用对称Hausdorff距离来评估的模型的几何相似度，对称Hausdorff距离实际上是2个网格模型之间的最大误差，对称Hausdorff距离越小，2个网格模型之间的几何相似度越大。从表1数据还可以看出，随着删除的顶点数的增加，对称Hausdorff距离增大，几何相似度下降。

表1 某地区地质模型试验数据

为了直观地表示试验结果中删除的网格点和保留的网格点，将该网格点转化为985×748的平面图像。对于每个模型，采用3种显示方式，分别为点显示（见图5）、网格显示（见图6）和三角面片显示（见图7）。可以看出，图5和图6清晰地显示了保留的网格点。此外，从图7的4幅图片可以看出，虽然顶点数减少，但模型的相似度仍然较高。

4 结语

提出一种通过对数据的简化来实现三维地质模型快速建模的算法，在一定的精度范围内，根据三角形面片的法矢量对一些数据进行删除，在数据处理的过程中，利用GPU强大的计算能力，对处理后的数据进行重构，达到快速建模的目的。试验结果表明，利用该方法能够在保证较高相似度的前提下实现模型的简化和建模速度的提高，因而该方法是可行的。

图5 各模型点显示图

图6 各模型网格显示图

图7 各模型三角面片显示图

［1］Wang Gongwen，Zhu Yanyan，Zhang Shouting，et al.3Dgeological modeling based on gravitational and magnetic data inversion in the Luanchuan ore region ［J］.Journal of Applied Geophysics，2012，80（1）：1～11.

［2］Tame C，Cundy A B，Royse K R，et al.Three－dimensional geological modelling of anthropogenic deposits at small urban sites：A case study from Sheepcote Valley ［J］.Journal of Environmental Management，2013，129（15）：628～634.

［3］李舒，李伟波，宋世鹏 .三维地质建模的应用研究 ［J］.科学技术与工程，2008，24（8）：9584～9587.

［4］刘少华，吴东胜，罗小龙，等 .复杂地质体的三维建模与可视化方法的研究 ［J］.矿业研究与开发，2007，27（2）：56～58.

［5］Wycisk P，Hubert T，Gossel W，et al.High－resolution 3Dspatial modelling of complex geological structures for an environmental risk assessment of abundant mining and industrial megasites ［J］.Computers ＆ Geosciences，2009，35（1）：165～182.

［6］Jing Ming，Mao Pan，Honggang Qu，et al.GSIS：A 3Dgeological multi－body modeling system from netty cross－sections with topology ［J］.Computers ＆ Geosciences，2010，36（6）：756～767.