基于马尔可夫链改进的世界钢铁消费量组合预测

郭培俊 （浙江工贸职业技术学院数学教研室，浙江 温州325003）

钢铁是国计民生的必需品，又是政府的限制品。如若盲目生产，事必导致企业生产能力更加过剩；如若停止生产，将导致市场对钢铁需求的缺乏及企业内部职工生活不稳定。因此，制定合适的生产销售计划显得尤为重要。需求决定市场，市场决定生产，所以预测未来钢铁需求量比了解钢铁生产量更加重要［1］。

阎建明等［1］构建了钢材需求分析模型（MSAD），利用钢铁行业历史数据分析预测了特定年行业产量；翁克勤［2］利用比较分析法，通过人均GDP将工业发展分为4个阶段，比较各发达国家的产业结构与人均钢材消费饱和点，分析了我国的人均钢材消费量饱和点，对我国工业化后期人口进行了估算，预测了我国工业化后期的钢材表观消费量；韦保仁［3］利用市场导向分析法，将钢铁市场划分为4个，对中长期的钢铁产量进行了分析预测；朱及天等［4］运用3种不同方法（比较法、线性回归法、增长率法）的结果取平均值法，预测了未来国内市场的钢铁需求；王礼［5］通过模型组合（弹性系数法、消费强度法、多元线性回归模型、灰系统模型），预测了“十二五”期间我国对钢的需求及其供需平衡；吴新春［6］建立生命曲线Verhulst模型，预测未来2015年中国粗钢消费量。以上几种对钢铁消费量预测模型，除了要用到较多的历史数据外，最大缺憾是没有进行误差分析，对模型的精度无从鉴定。而对于未来数据的预测往往与就近年代的数据关联性最强，且要求预测精度尽量高。

GM（1，1）模型［7］是最为常用的预测模型之一，基于随机的原始时间序列，按时间累加后形成新的时间序列，呈现的规律可用一阶线性微分方程逼近。经证明，当原始时间序列隐含着指数变化规律时，用GM（1，1）模型预测非常成功。

笔者所研究的世界钢铁消费量，其数据在2007～2010出现了上下波动，且原始数据有限，若单一使用GM（1，1）模型来预测，仅适用于短期预测，且模型值比较粗糙；若用适合于长期预测的多项式模型来进行平衡或矫正，预测结果准确率将大有改进；利用首次的综合预测结果，再结合马尔可夫链预测方法，把点预测改进成有一定可信度的区间预测，有望进一步提高预测的有效性［8～10］。

马尔可夫链预测方法的基本思路则是通过原始数据序列求得序列的状态转移矩阵，再根据状态转移矩阵对未来变化趋势做出估计［11］。因此，可以通过对组合预测模型结果进行马尔可夫链改进来提高预测的准确性，即“组合－马尔可夫链”预测。对于组合模型得到的预测结果，根据马尔可夫链方法获得组合模型在已知年份里的偏差规律（即偏差的状况转移矩阵），依照此规律对组合模型结果进行修正，将组合模型预测的结果由数值修正为区间和概率组成的预测范围，增加预测的可信度。

1 GM（1，1）模型

设对数列x（0）＝（x（0）（1），x（0）（2），…，x（0）（n））建立的一阶线性微分方程为：

该方程的白化解为：

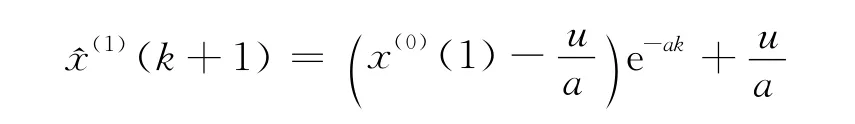
GM（1，1）动态预测模型：

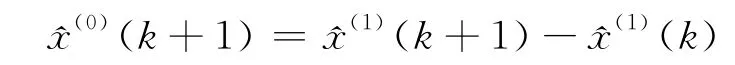
k点的残差p（k）和相对误差ε（k）分别为：

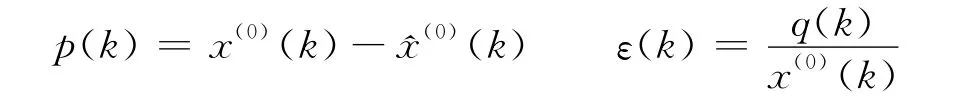
同理，对于组合模型，也先求出相对误差ε（k）。

把相对误差分成5个状态（见表1），根据频数算出对应的状态概率：

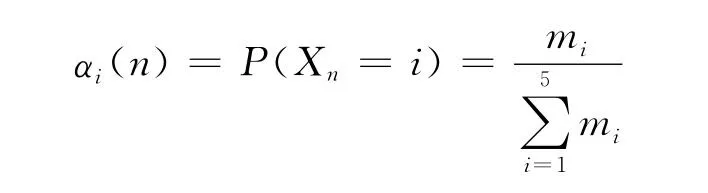
根据状态间的转移情况及转移次数算出相应的转移概率：

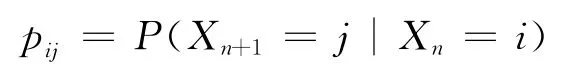
表1 相对误差5种状态

2 马尔可夫链

马尔可夫链基本方程为：

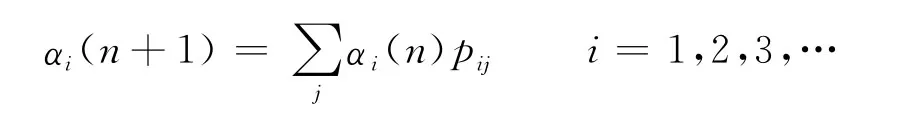
其中，αi（n）和pij满足：

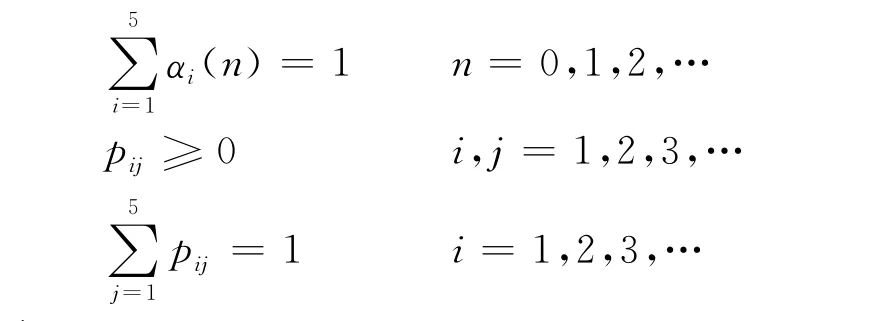
记：

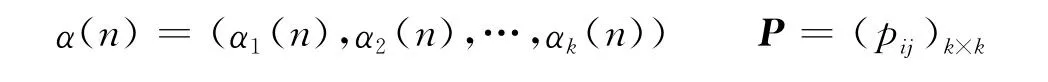
则马尔可夫链基本方程可表示为：

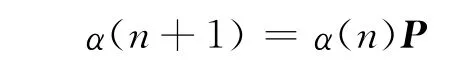
由此可以得到：

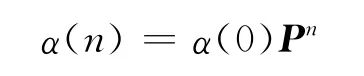
3 实例分析

3.1 数据的获取

国际钢铁协会（Worldsteel.org）是全球最大最有活力的工业组织之一，会员包括64个国家170家钢铁生产企业，这些国家是世界钢铁产品的最大消费国，国际钢铁协会会员的钢铁产量占到全世界的85%左右。由于最近期一个版本数据只能查到7年之内的信息，且7年前当年的资料在先后2个版本中不一样，在新一版本中会有所调整，所以2003～2005年的资料要分别查用3个最近版数据。如2003年数据要通过7年后的2010年版本落定，而2004和2005年数据要分别用2011年和2012年版本。通过搜集4个版本的《世界钢铁统计数据》，共得到从2003～2012年共10年的钢铁表观消费量，具体数据见表2。

3.2 GM（1，1）模型建立及求解

取原始资料作数列：

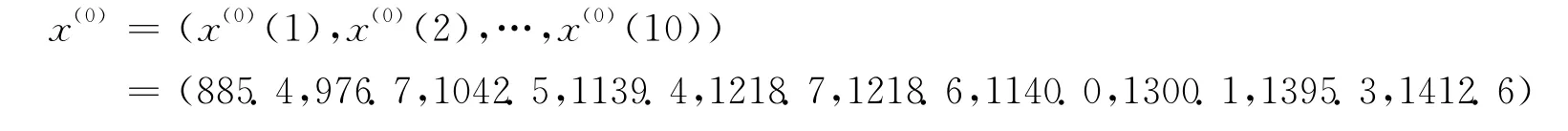
作一次累加得：

以x（0）为基础构造Y＝（x（0）（2），x（0）（3），…，x（0）（10）），即：

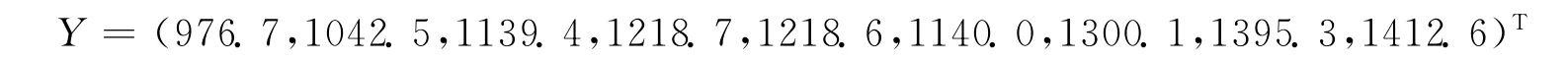
利用加权算术平均数法对数列x（1）中的数据作进一步的平滑（二项平均），具体采用公式λx（1）（k－1）＋（1－λ）x（1）（k），一般取加权系数λ＝0.5对x（1）中的数据进行平滑，平滑后的新数据填入下面矩阵B中的第一行：

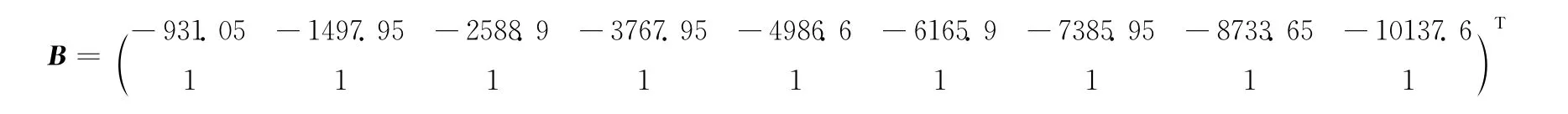
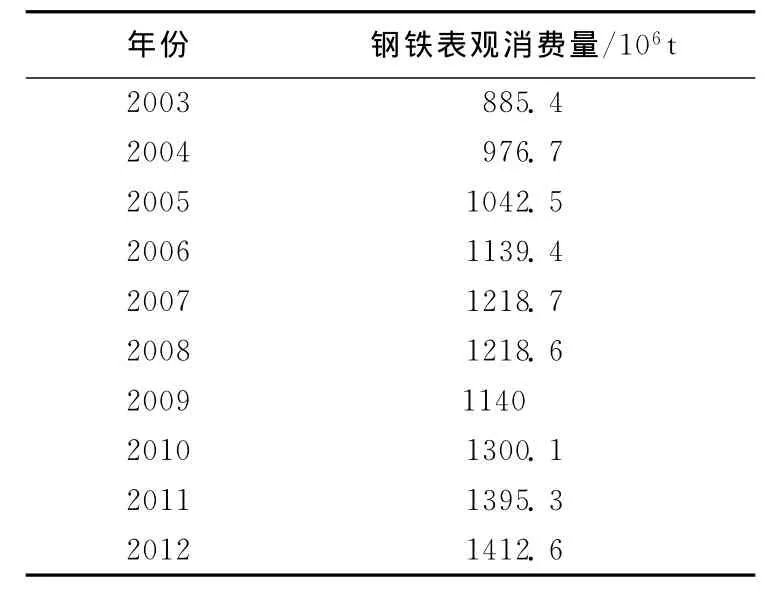
表2 2003～2012年世界钢铁表观消费量

用Matlab软件编程计算得：

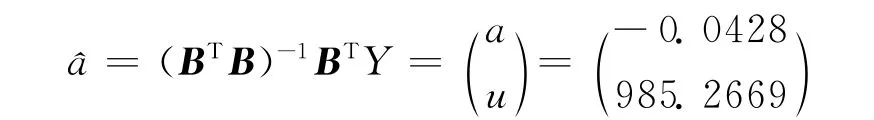
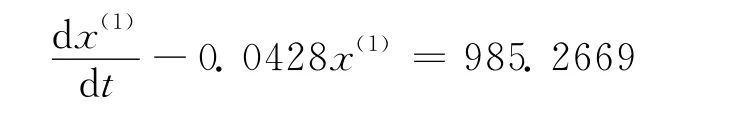
代入（1）（k＋1）＝得：

即：

由于：

且规定（0）（1）＝（1）（1）＝885.4。

根据式（1）、（2）计算出模型值，结果见表3。对模型值进行残差和相对误差检验，平均相对误差＝3.885%。2009年的残差和相对误差都明显偏大，这与2008年金融危机的惯性影响导致世界钢铁消费量突然下降密切相关。

3.3 多项式拟合

用2003～2012年的原始值，分别采用一次、二次、三次多项式拟合，拟合函数分别为：

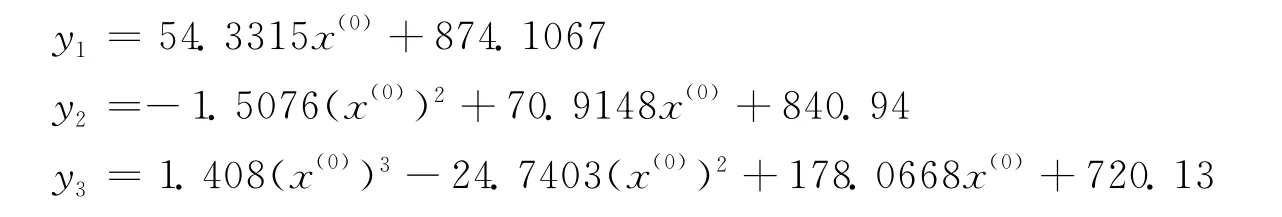
拟合平均相对误差分别是：＝3.11%，＝2.77%＝2.67%，都小于5%，说明模型精度均高。

3.4 组合模型

由于二次多项式、三次多项式的趋势分别是凸的和凹的，而一次多项式是直线型的，且它们都属于长期趋势预测，所以把这3个拟合函数和短期趋势预测GM（1，1）模型组合起来进行预测。组合模型为：

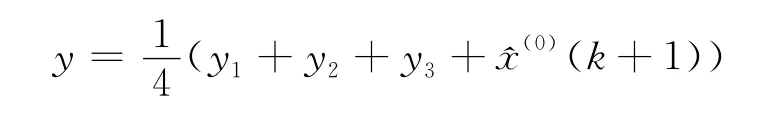
模型结果如表4所示，4种模型的拟合曲线见图1所示。

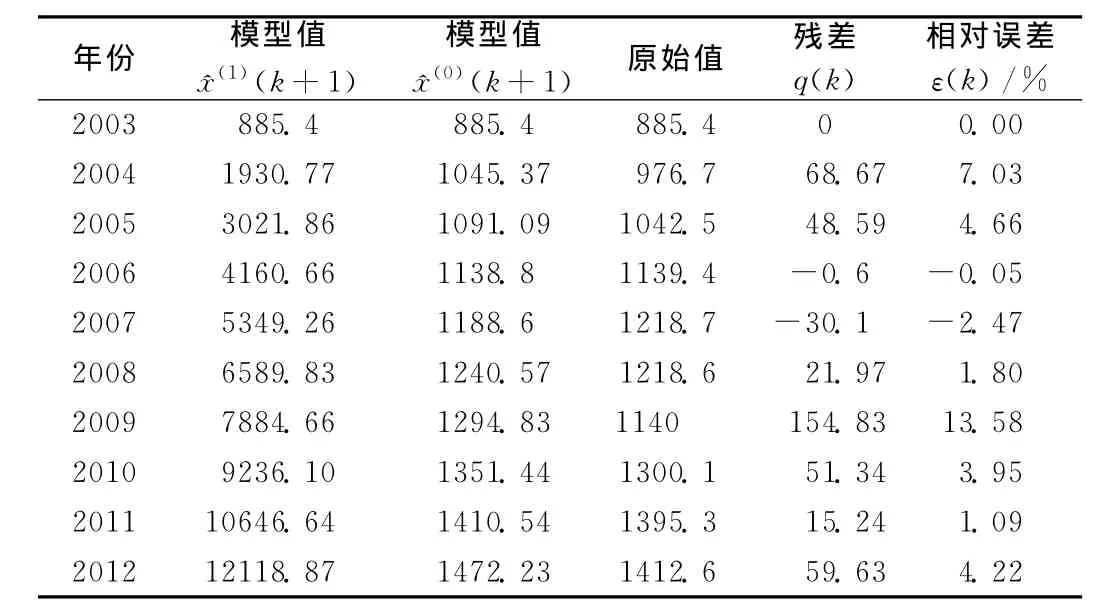
表3 GM（1，1）模型值检验结果

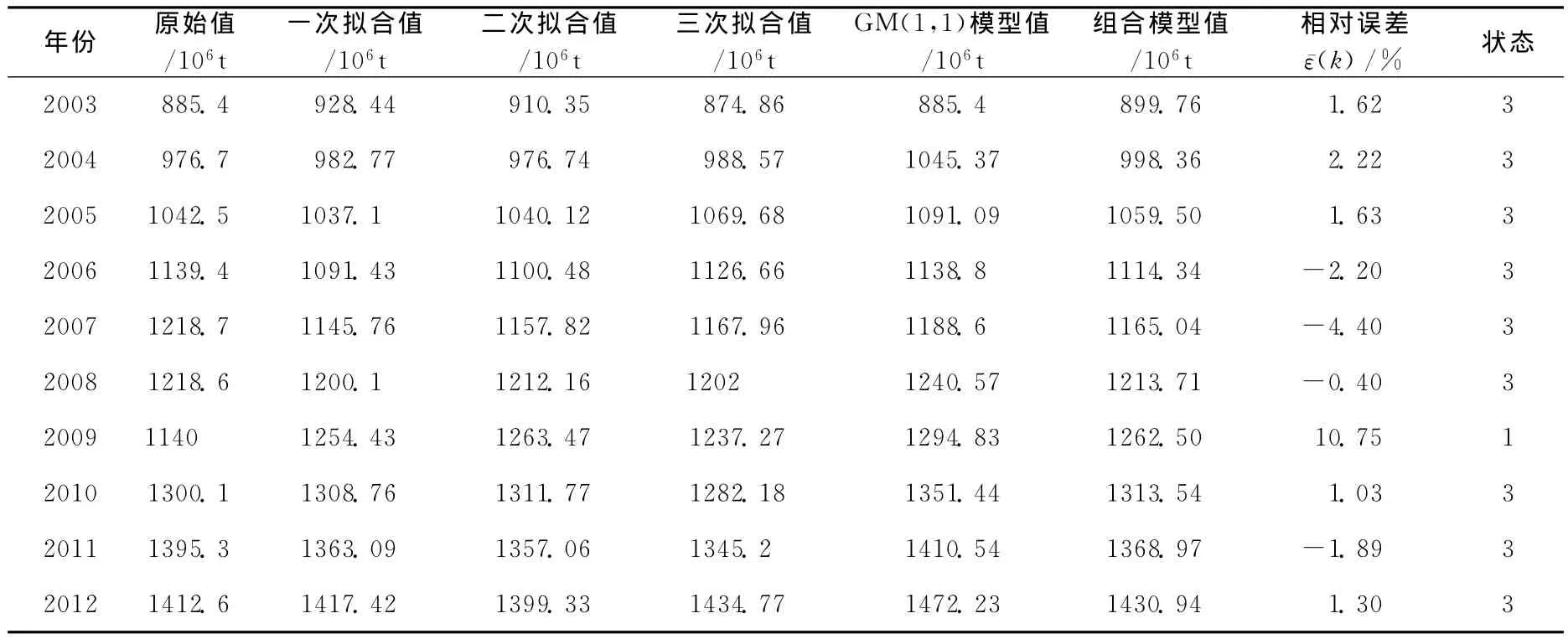
表4 4种模型值平均相对误差构成状态

总平均相对误差为＝｜（k）｜＝2.74%。

3.5 组合模型的马尔可夫链改进

针对表4所设状态，得到2004～2012年状态转移情况，如表5所示。

由此得相应的状态转移矩阵：

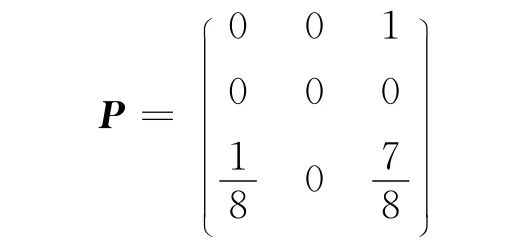
由状态转移向量公式α（n）＝α（n－1）P＝α（0）Pn和2012年的状态向量α（0）＝（0，0，1），计算得马尔可夫链状态向量，如表6所示。

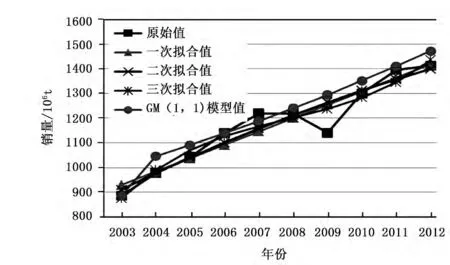
图1 4种模型的拟合曲线

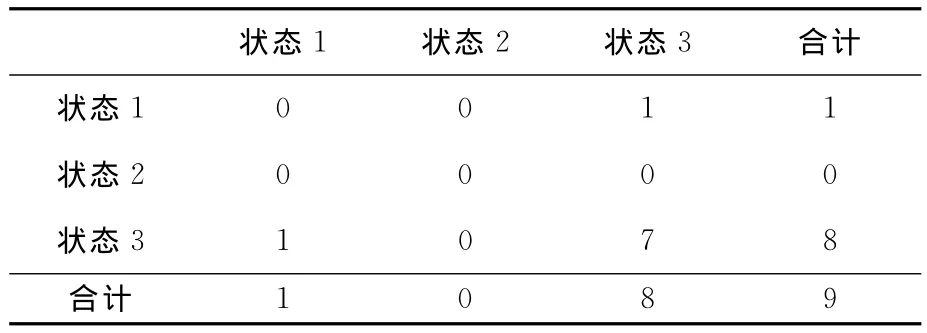
表5 状态转移

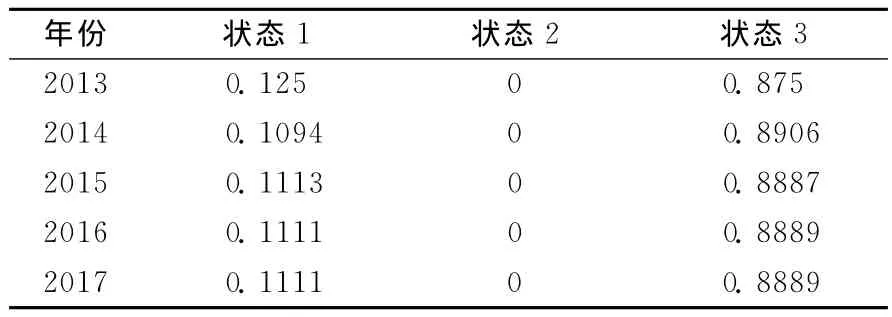
表6 2013～2017年钢铁需求量预测结果的马尔可夫链状态

现把4种方法预测结果及组合预测值汇总，如表7所示。

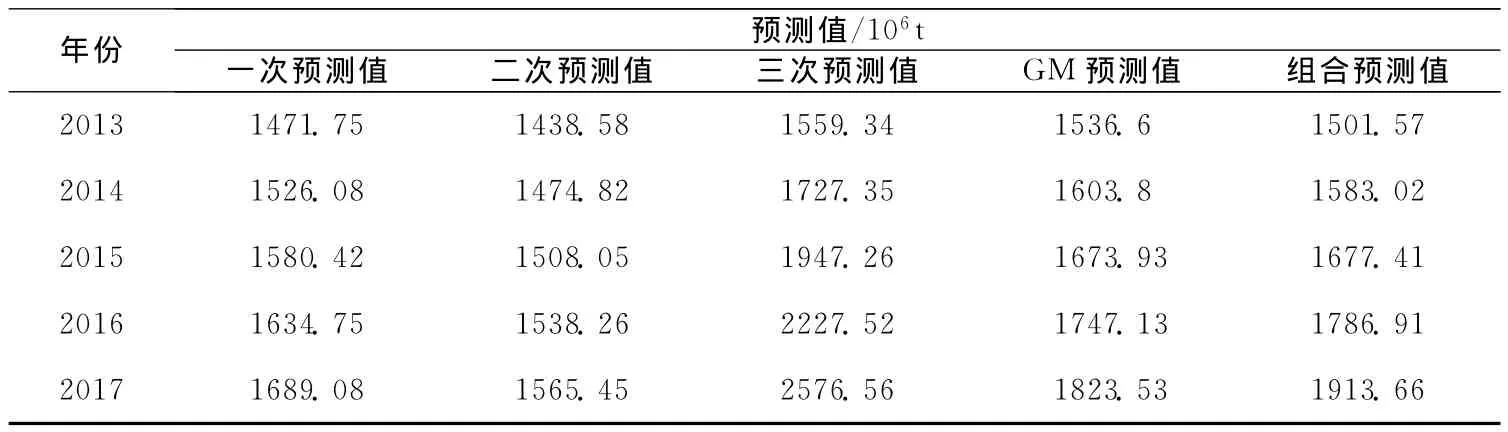
表7 4种方法预测结果及组合预测值汇总表

按照状态1、2、3在各年份分别出现的概率大小，对组合预测结果（预测中值）进行分区间处理，其预测区间如表8所示。预测结果，采用保守原则，可取预测区间的最小值；若用乐观原则，则取预测区间的最大值。其预测结果如图2所示。

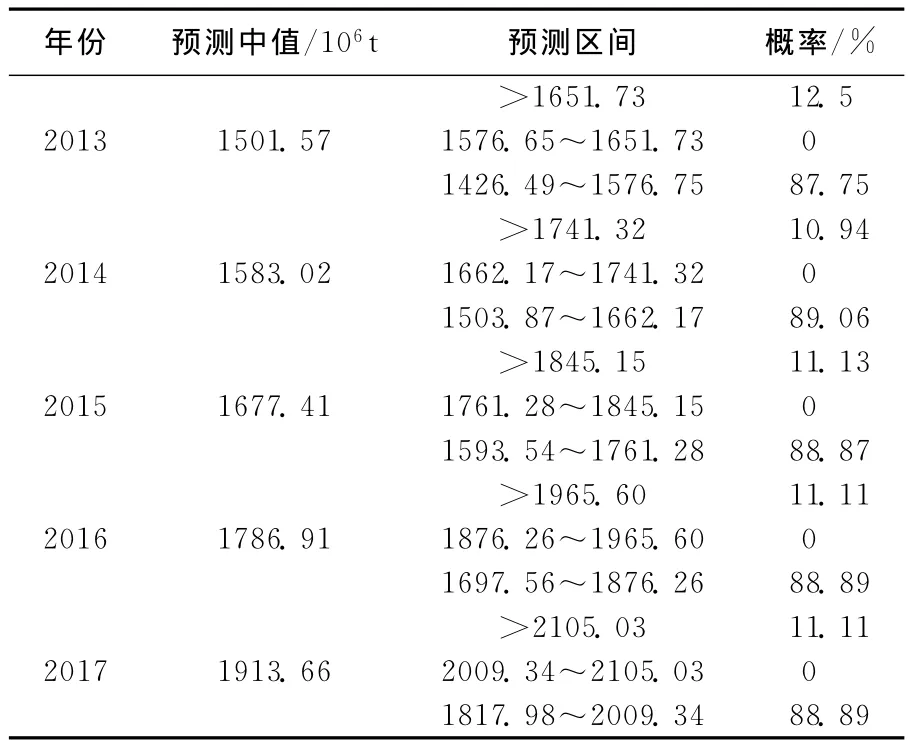
表8 2013～2017年世界钢铁消费量组合预测马尔可夫链改进结果

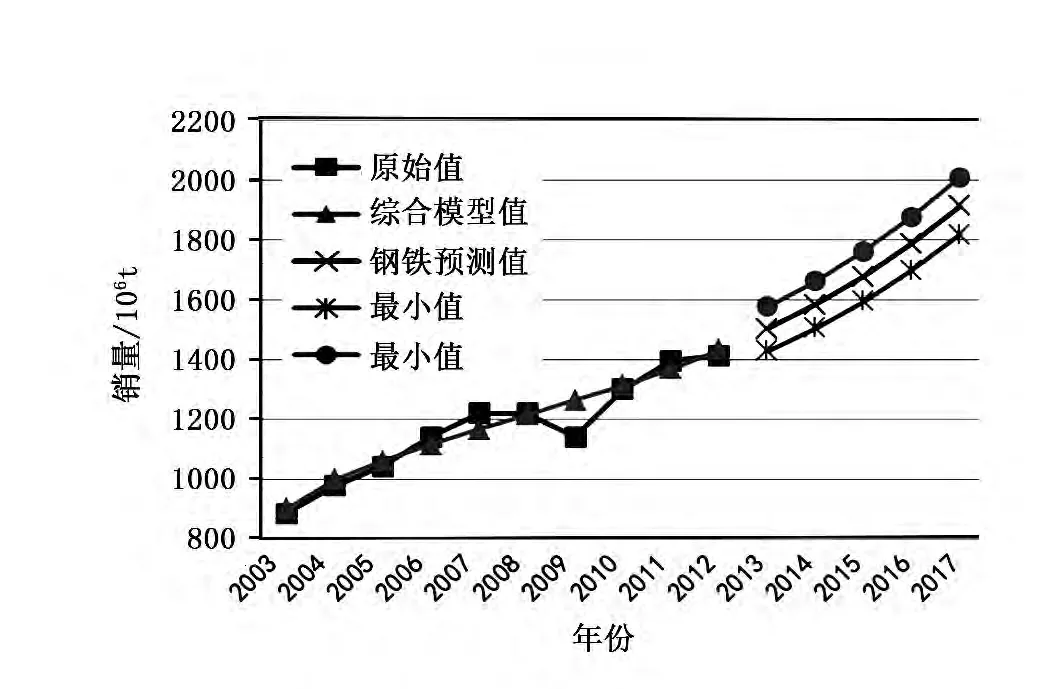
图2 世界钢铁表观消费量及预测结果

国际钢铁协会在第47届年会上发布的2013～2014年全球钢铁业短期展望报告。该报告中显示，2013年全球钢材表观消费量将达14.75×108t（1475×106t）［12］，在模型的预测范围1426.49～1567.75内（可信度87.75%）；2014年将达15.23×108t（1523×106t），也在模型的预测范围1503.87～1662.17内（可信度89.06%），且是保守预测。

［1］阎建明，蒲刚清，刘贞，等 .基于分行业级别的钢铁需求预测研究 ［J］.科技管理，2008（12）：254～258.

［2］翁克勤.2006～2020年我国铁矿石进口量预测 ［J］.港口经济，2006（5）：46～49.

［3］韦保仁 .中国钢铁生产量及其能源需求和CO2排放量情景分析 ［J］.冶金能源，2005（6）：3～6.

［4］朱及天，洪天求 .我国钢铁需求预测及铁矿资源安全供给对策 ［J］.金属矿山，2006（10）：9～12.

［5］王礼 .中国对钢铁资源的长期需求预测 ［J］.地质与勘探，2012（6）：1129～1133.

［6］吴新春.2015年中国钢铁需求预测 ［J］.武钢技术，2012（4）：1～3.

［7］邓聚龙.灰色预测与决策 ［M］.武汉：华中理工大学出版社，1986：125～134，150～159.

［8］苏永东，李必鑫 .王智源 .基于马尔可夫改进方法的我国石油需求量预测 ［J］.军事物流，2009（11）：112～114.

［9］汪同三，张涛.组合预测——理论、方法及应用 ［M］.北京：社会科学文献出版社，2008：1～85.

［10］平狄克，鲁宾费尔德 .计量经济模型与经济预测 ［M］.北京：机械工业出版社，2007：1～100.

［11］姜启源，谢金星，叶俊 .数学模型 ［M］.北京：高等教育出版社，2009：333～356.

［12］世界金属导报 .国际钢协：2013年全球钢材表观消费量同比增长3.1% ［EB／OL］.http：／／www.worldmetals.com.cn／hyyw／201310／t20131014＿244529.htm，2013－10－14.