基于合图法（co-plot）的我国省际知识产权效率分析

柳春岩，罗 旭

（兰州理工大学 经济管理学院，甘肃 兰州 730050）

知识产权又称智慧财产权（Intellectual Property Rights，IPR）是指权利人对其所拥有的知识资本在有限时期内享有的专有权利。知识产权不仅是一种重要的法律权利和无形资产，也日益成为企业竞争的重要资源。

一、文献综述

知识产权的评价方法很多，通常采用知识产权指数的方法来分析、评估知识产权的竞争能力。根据范围和内容的不同，知识产权评估方法分为企业知识产权评估和区域知识产权评估两种。

2000年3月，欧盟出台包括人力资源、新知识的产生、新知识的转移和应用及创新的投入、产出和市场等4类，共计17项指标的新评价指标体系。[1]瑞士洛桑国际管理开发研究院连续多年发表的《世界竞争力年鉴》包括R&D支出、R&D人员、技术管理、科学环境、知识产权等五个子体系[2]，共计25个指标。2004年日本《知识产权战略评价指标》[3]，以专利的收益率、成果转化利用率、人均研究开发经费和知识产权的经济产出作为战略实施的评价指标。2007年国际知识产权联盟（IPRA）发布世界知识产权指数（International Property Rights Index）。目前共连续发布六版IPRI，2012年涉及国家达到129个。[4]IPRI由三部分，共计10指标构成。

国内学者对知识产权评价体系也进行了广泛研究。

黄庆等（2004）[5]从专利数量、质量和价值三方面综合考虑，构建了一套以数量类指标表征专利关注程度，以质量类指标表征科技创新程度，以价值类指标描述专利在市场经济活动中作用的指标体系，对我国区域的知识产权状况进行了评价。刘凤朝（2009）[6]选取专利申请量、发明专利申请量、专利授权量和发明专利授权量作为分析评价指标，运用主成分分析方法对我国31个省市区和15个副省级城市的专利发展状况进行综合排序、等级划分和评价。王正志（2010）[7]建立了一套包含多层次、多指标的中国知识产权指数体系，对我国知识产权发展过程进行研究分析，多年相继发布《中国知识产权指数报告》。王鸣涛、叶春明（2010）[8]采用AHP和专家咨询相结合的方法，提出以知识产权申请、知识产权授权、知识产权实施、知识产权效益、知识产权保护、知识产权管理和知识产权环境为一级指标，涵盖27个二级指标的区域知识产权工作业绩评价指标体系。雒园园等（2011）[9]通过知识产权质量、知识产权数量、知识产权开发能力、知识产权运营能力、知识产权保护能力5指标构建了区域知识产权竞争力评价指标体系。罗旭（2013，2014）[10-11]通过对中国知识产权指数的区域差异及与区域经济绩效分析发现：知识产权指数的区域差异突出，东部地区的知识产权实力指数是西部地区的2倍多。知识产权指数与人均GDP具有明显的相关性，知识产权指数增长0.1，将产生人均近一万元GDP增长。并通过Malmquist指数对我国省际知识产权全要素生产率增长进行了分析。

对相关文献进行梳理，可见国内外对知识产权指数的研究更多是从国家宏观层面上展开，侧重点也不尽相同。虽然数理模型多种多样，但直观的图形化的方法并不多见。本文采用合图法（co-plot）对《中国知识产权指数报告2013》的相关数据进行图形分析。图形直观地表明了2012年我国31省市区知识产权效率值分布状况。

二、生产率效率的非参数估计

数据包络分析（DEA）是由 Charnes，Cooper和 Rhodes（1978）提出，逐步发展为多种模型的一种非参数分析方法，采用DEA方法的主要优势是它不需要确定的生产函数形式。

可变规模收益时的标准非参数DEA模型：

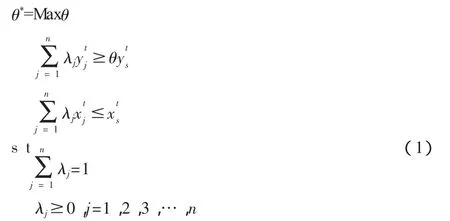
超效率非参数DEA模型：

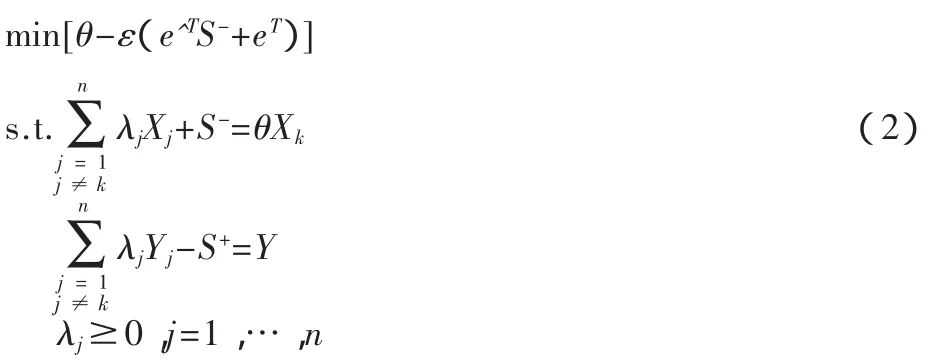
ε是非阿基米德小量，S-，S+是投入与产出的松弛变量。

本文采用《中国知识产权指数报告2013》中的综合实力指数作为产出指标。并使用相同年份的《中国科技统计年鉴》的三项统计指标：科研经费投入、科研人员投入及科研时间投入作为投入指标、来分析2012年我国31省市区知识产权效率分布状况。

即采用3投入1产出计算可变规模DEA和超效率DEA模型效率值（见表1）。

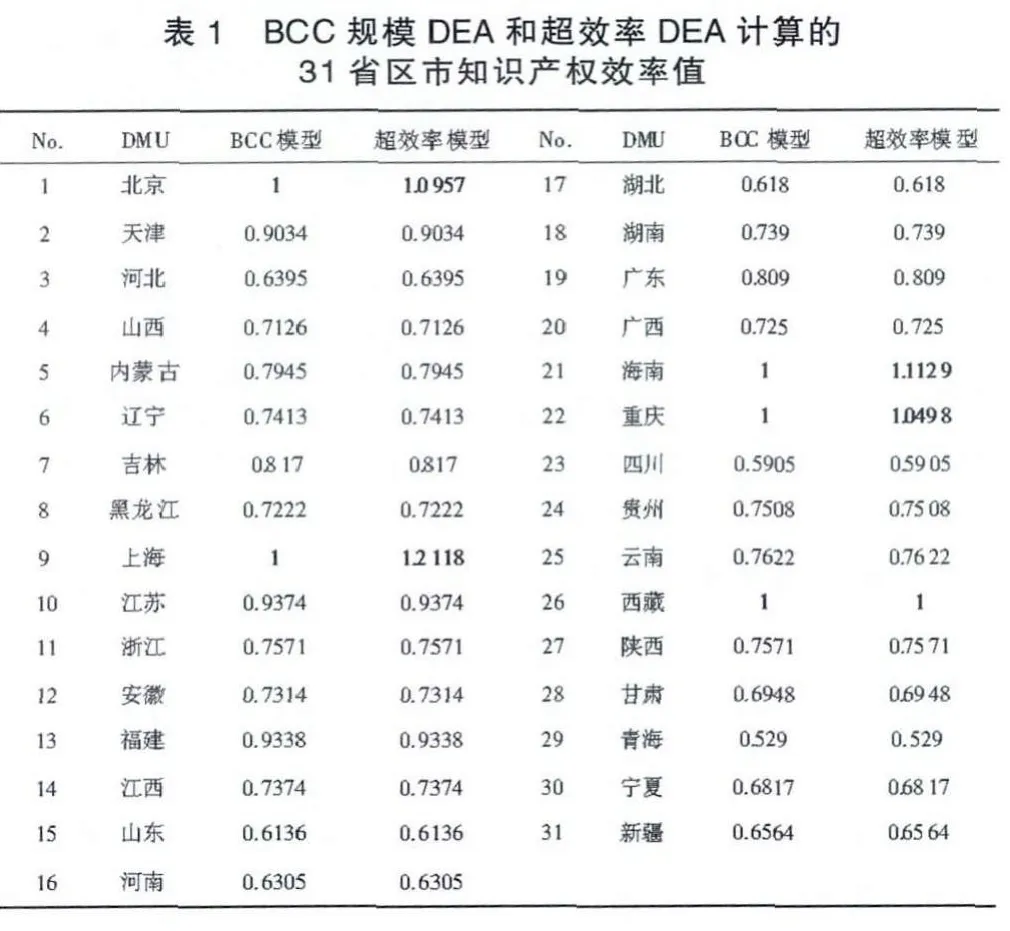
分析可知，通过可变规模DEA模型计算的31省市区知识产权效率值有5个省区市（北京、上海、重庆、海南、西藏）处于效率前沿面上，效率值为1，其余省市区都是无效的。而这5个DMU经济、社会发展差距突出，通过超效率DEA模型可以较好地区分这5省区市效率值的差异。

三、合图法

Co-plot方法[12]是由Ad.i Raveh1996年提出的，并很快应用于多个领域研究之中。[13-15]与传统的统计软件excel和层次聚类法相比较，co-plot法在研究对象多元聚类分析中具有自己独特的优势。合图法是对数据矩阵Yn×m进行图形展示，n个研究对象（即DMU）被定为n个点，m个变量基于同一轴线和同一原点以m个箭头显示。通过合图法，具有相似特征的研究对象（即DMU）较为紧密地展示在图上，而每个变量则以不同的箭头单独体现，通过两箭头间的夹角关系来分析其相关性。即处于相同方向的箭头表明正相关，如果两箭头形成180°表明两变量为负相关，若两箭头成90°垂直表明其不相关。合图法以两图依次重叠而成。第一幅图显示n个研究对象的n个不同区位，第二幅图基于第一幅图的基础上以各个箭头展示m个属性有关信息。合图法使用的主要目的是得到一个包括n个研究对象及其m个变量的对应数据矩阵Yn×m的图形。

合图法分为四个步骤：

①标准化数据矩阵：

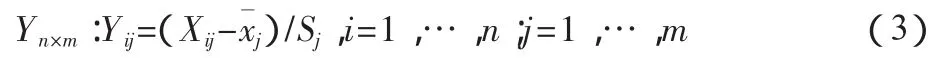
②研究指标差异性测度：

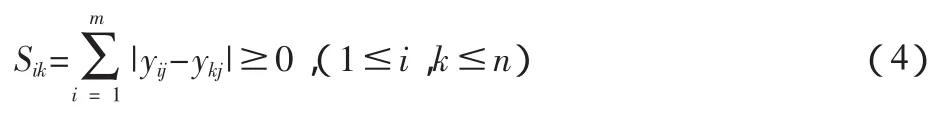
③图形展示：采用最小空间分析法（SSA）对n个研究指标进行图形展示，借助关系疏离指数θ，SSA可以判断图形模拟的精确性。通过生成2n个（X1i，X2i），i=1，2，…，n，使每一行Y=（Yi1，…，Yim）能够在二维空间（X1i，X2i）中以点的形式展现出来。

④形成由研究变量组成的m个箭头：每个研究变量的实际值和在箭头轴上的投影的相关程度最大化，由于高度相关的变量在图形上呈现方向一致。两两箭头的夹角余弦值比例与箭头之间的相关程度成比例。

借助两个系数可以检验合图法形成图形的拟合程度。一个是步骤③中的θ，另一个是步骤④中的m个变量最大相关系，在展示图形中，那些拥有较低rj的变量将会被剔除。根据经验当θ≥0.15或，拟合程度较低时，得出的图形难以正确反映数据所包含的信息。一般而言，合图法的运用对n和m的数目并没有严格限制，但当n＞200和m＞50时，很多细节信息在图形中尚无法展示。

四、数据及图形分析

（一）数据矩阵

通常DEA与Co-plot是通过比例关系联系在一起的。我们定义3个产出/投入比率rkj如下：

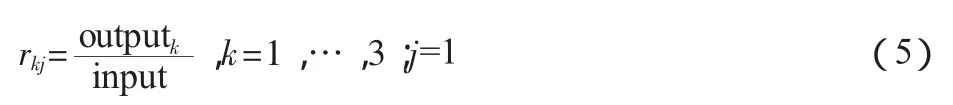
Input分别是科技经费投入额（亿元）、科技人员数（万人）和研发人员全时当量（万人年）；output为知识产权指数。分别得到三个变量（比率值）：科技投入（亿元）创造的知识产权指数值，科技人员（万人）创造的知识产权指数值，研发人员全时当量（万人年）创造的知识产权指数值。将31×3矩阵代入，绘制co-plot图（见图1）。

图1 31省市区在三变量上的合图法

（二）co-plot图形分析

1.31省市区在三变量上的合图法。在图1中31个省区市分布在两个维度空间中，反映图形拟合程度的两个检验系数：离散度 θ=0.01，最大相关系说明拟合程度很高。通过观察我们可以发现：

（1）三个变量间联系紧密，尤其是科技人员数（万人）创造的知识产权指数值和研发人员全时当量（万人年）创造的知识产权指数值。

（2）31省市区中巨大部分都分布在三变量的重心周围。西藏和海南两省区是离群极值，是有效率的，其他有效率的省市（北京、上海和重庆）分布在大量的无效率省市区中。青海和宁夏两省区也是离群值，是无效率的，且效率值较低。宁夏略高于青海，但青海在科技人员（万人）创造的知识产权指数值指标上高于宁夏。与可变规模收益DEA，超效率DEA模型结果一致。

（3）剩余的27省市区分为两个组群：A组包括贵州、新疆、甘肃、内蒙古、重庆和江西，其余21省市区为B组。为了更清晰准确直观地分析，我们把A、B抽出，单独进行分析。

用A组6省市区相关数据构成一个6×3的矩阵，代入绘制co-plot图（见图2）。

2.6省市区在三变量上的合图法。在图2中6个省区市分布在两个维度空间中，反映图形拟合程度的两个检验系数：离散度 θ=0.01，最大相关系说明拟合程度很高。通过观察我们可以发现：

（1）研发人员全时当量（万人年）创造的知识产权指数值与科技人员数（万人）创造的知识产权指数值和科技投入（亿元）创造的知识产权指数值均保持密切联系。

（2）江西是离群值，远离三指标变量的重心，也是无效率值。在三个指标变量上，得分较低。

图2 6省市区在三变量上的合图法

（3）新疆、贵州在科技投入（亿元）创造的知识产权指数值上得分相对较高。

（4）内蒙古、甘肃和重庆三地在科技人员（万人）创造的知识产权指数值指标变量上得分相对较高，重庆也是有效率值的。

B组21省市区相关数据构成一个21×3的矩阵，代入绘制co-plot图（见图 3）。

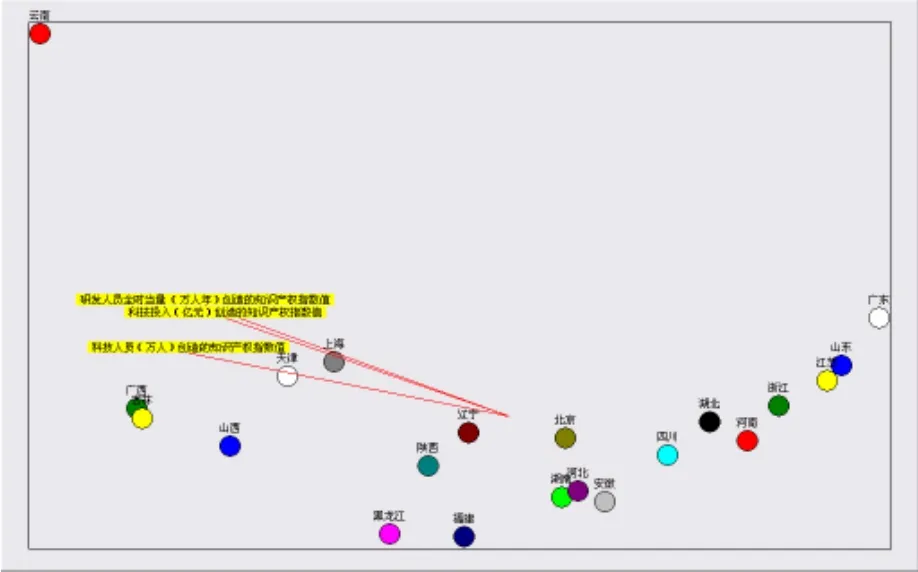
图3 21省市区在三变量上的合图法

3.21省市区在三变量上的合图法。B组主要是东、中部地区省份。反映图形拟合程度的两个检验系数：离散度θ=0.05，最大相关系说明拟合程度很高。通过观察我们可以发现：

（1）研发人员全时当量（万人年）创造的知识产权指数值指标变量与科技投入（亿元）创造的知识产权指数值指标变量联系更为密切。

（2）云南是离群值，远离三指标变量的重心，也是无效率值。在科技投入（亿元）创造的知识产权指数值指标变量上，得分较高。

（3）天津在科技人员（万人）创造的知识产权指数值指标变量上得分较高。上海在研发人员全时当量（万人年）创造的知识产权指数值指标变量与科技投入（亿元）创造的知识产权指数值指标变量上，有上佳表现。

（4）广西、吉林和山西在科技投入（亿元）创造的知识产权指数值指标变量和科技人员（万人）创造的知识产权指数值指标变量上得分相对较高。

（5）广东、山东和江苏在科技人员（万人）创造的知识产权指数值和科技投入（亿元）创造的知识产权指数值两指标上表现不佳，得分较低。

（6）福建、黑龙江两省在三个指标变量上得分比较低。北京和辽宁在三指标变量的重心附件，表明它们的得分比较平均。剩余的其它各省区得分则比较低。

五、研究结论

本文采用合图法（Co-plot）直观分析了基于DEA模型计算的2012年我国省际知识产权相对效率值及其相关指标变动特点。合图法是对Yn×m的数据矩阵进行图形展示，每一个DMU表现为二维空间的一个点，每一个指标变量体现为源于（m个指标变量）重心的一条射线。通过比例关系设定，与其它的图示方法相比，合图法（Co-plot）的明显优势就是可以同时分析DMU和指标变量。把DEA和合图法（Co-plot）联系起来，通过解读3张合图，不仅可以直观、清晰地分析31个省市区在知识产权相对效率值方面的分布及变化，更能进一步分析其在三项指标变量上的优劣和特点。

[1]杨平.欧盟建立创新评价指标体系及其与美日的比较[J].科技经济透视，2002（8）：24-25

[2]陈昌柏.借鉴国际经验设置我国知识产权战略评价指标[EB/OL].http：//www.chinado.cn/ReadNews.asp?NewsID=935.

[3]王绍媛.日本知识产权战略特点与借鉴[J].现代日本经济，2009（6）：40-44.

[4]Gaurav Tiwari.2011 report international property rights index property rights alliance，2011.

[5]黄庆，曹津燕.专利评价指标体系——专利评价指标体系的设计和构建[J].知识产权，2004（5）：25-28.

[6]刘凤朝，徐冠华.国家创新能力测度方法及其应用[M].北京：科学出版社，2009.

[7]王正志.中国知识产权指数报告2009/2011/2012[M].北京：知识产权出版社，2009/2011/2012/2013.

[8]王鸣涛，叶春明.区域知识产权工作业绩评价指标体系研究[J].科技管理研究，2010（21）：47-53.

[9]雒园园，田树军，于小丹.区域知识产权竞争力及评价指标体系研究[J].科技管理研究，2011（14）：68-75.

[10]罗旭.中国知识产权指数的区域差异及与区域经济绩效分析[J].科研管理研究，2013（23）：120-122.

[11]罗旭，柳春岩.基于DEA-Malquist指数的我国省际知识产权全要素生产率增长分析[J].科研管理研究，2014（22）：38-42.

[12]LipshitzG，Raveh.A Applications of the Co-plot Method in the Study of Socioeconomic Differences Among Cities[J].Urban Studies，1996，31（1）：123-135.

[13]Adi Raveh.Co plot：A Graphic Display Method for Geo metrical Representations of MCDM[J].European Journal of Operational Research，2000，125（3）：670-678.

[14]马秋芳，杨新军，孙根年.合图法（co plot）在入境游客期望感知分析的应用[J].系统工程理论与实践，2008（4）：167-171.

[15]马秋芳，杨新军，王军伟.基于游客的旅游资源分类及旅游空间模型构建[J].地域研究与开发，2009，28（4）：81-84.