随机时滞电力系统稳定性分析

厉文秀

（河海大学 能源与电气学院，南京 210098）

1 随机时滞问题的产生

在自然界，系统状态的未来发展趋势往往既取决于当前运行状态，也与过去的状态密切相关，这类现象称为时滞现象。时滞现象在电力系统的控制回路中非常普遍，在过去分析电力系统时，往往忽略时滞的影响，这主要是因为控制器由本地量构成，此时的通信延时在10ms以下。但是，随着互联电力系统规模和复杂度的不断增加，大量功率需要远距离传输，区域间功率振荡的可能性和危害性日益增加，仅靠局部反馈信号设计的控制器越来越难保证互联电力系统的稳定性，必须充分利用广域量测系统所能提供的远方设备信息，进行系统协同控制，方能确保系统的安全稳定运行。而广域量测信息存在明显的延时，不能完全忽略，因此研究时滞环节对系统稳定性的影响，具有十分重要的现实意义。

关于时滞的研究主要集中在讨论系统的平衡点稳定性。文献［1］指出，对于给定时滞τ，只要线性时滞系统x·（t）=Ax+Bx（t-τ）没有位于右半平面某个矩形区域内的特征根时，系统就是渐近稳定的，这里的特征根是超越方程|sI-ABexp（s-τ）|=0的根。文献［2］指出当系统时滞较小时，n维线性时滞系统的n个特征值在相应的无时滞系统的特征值附近，时滞系统的最危险特征根派生于无时滞线性系统的最危险的特征根。在时滞不大的情况下，文献［3］通过求解超越方程获取系统的n个特征值，并将“所有特征根都位于复平面左半平面”作为系统稳定的充要条件。文献［4］在文献［3］的基础上，讨论了时滞因素对电力系统小扰动稳定域的影响。此外，不少文献将纯时滞环节在频域中用有理函数来近似，从而把系统的线性状态空间方程由无理方程变为有理方程。文献［5-7］用Pade表达式近似来描述系统的纯时滞环节，并在此基础上设计了阻尼控制器。

现实生活中电力系统总是存在着各种各样随机干扰，这些干扰有的是由扰动引起的系统内部结构、参数变化，有的是由可再生能源、电动汽车等接入引起的外部随机激励。当前随着可再生能源的大规模并网，其随机性对电力系统的影响不容忽略，有必要研究随机因素作用下电力系统的稳定性问题。

近年来随着随机H∞控制问题的解决，随机时滞系统的稳定性和鲁棒控制问题的研究取得了一定进展，出现了一些新的研究成果。文献［8］研究了一类带Markovian切换的非线性时滞随机系统的稳定性问题；文献［9，10］通过使用模型转换和线性矩阵不等式的方法，研究了一类时滞不确定随机系统的平均时间延迟和指数稳定性的鲁棒控制；文献［11，12］研究了不确定随机系统的鲁棒稳定性条件。

目前在电力系统领域，随机时滞系统的稳定性研究还未见报道。本文以励磁系统输入信号延时作为时滞环节，以可再生能源发电和电动汽车接入电网引起的功率波动作为电力系统的外部随机激励，建立单机无穷大随机时滞系统的数学模型；仿真获得随机时滞电力系统的受扰轨迹，分析不同时滞、不同扰动强度下随机时滞电力系统的稳定性；将时滞环节用Pade变换近似，计算时滞系统在平衡点附近的特征根，分析时滞系统在平衡点附近的动态特性；对比仿真结果与特征根结果，表明扰动强度较大时基于Pade近似的特征根结果与随机扰动下的仿真结果有较大的差异。

2 随机时滞电力系统模型

以图1所示的单机无穷大系统为例。其中发电机采用三阶实用模型，计及励磁系统动态。发电机d，q坐标下数学模型（采用标么值）为［13］：

图1 OMIB系统

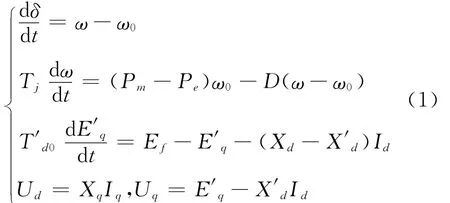
式中Ud，Uq——定子d轴和q轴电压；Id，Iq——定子d轴和q轴电流；Xd，Xq——d轴和q轴同步电抗；E′q——q轴暂态电势；X′d——d轴暂态电抗；δ，ω——发电机转子的功角和角速度；ω0——角速度的初始稳态值；Tj——发电机的惯性时间常数；Pm——机械功率；Pe——电磁功率；D——阻尼系数；T′d0——d轴的暂态时间常数；Ef——励磁电势。

根据发电机的电压向量图［14］，可以得到

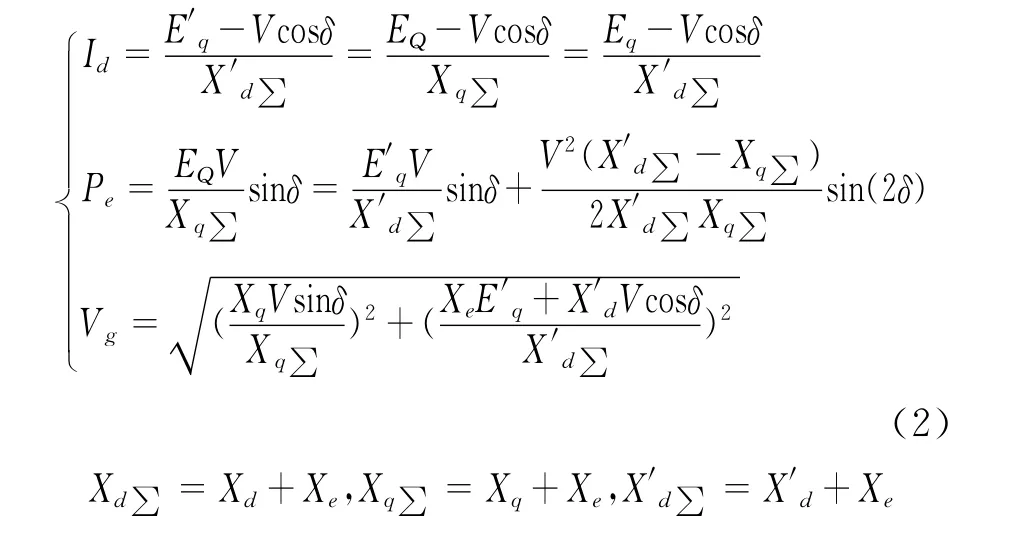
式中Xe——发电机到无限大母线之间的电抗；EQ——假想电动势；Eq——空载电动势；V——无穷大母线电压；Vg——励磁系统端电压。

2.1 含时滞环节的OMlB系统

励磁系统的数学模型用一阶惯性环节表示，其等值放大倍数为Ka，时间常数为Ta。为了研究时滞对OMIB系统稳定性的影响，在励磁系统的端电压反馈通道加上纯时滞，如图2所示，延迟时间为τ。

图2 励磁系统框图

该励磁系统的动态方程为：

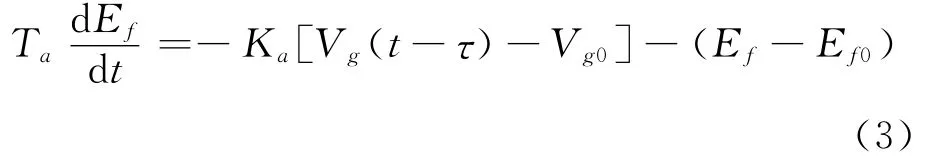
结合式（1）～式（3），可以得到时滞OMIB系统的状态空间模型：

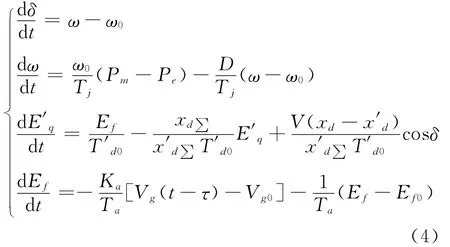
2.2 随机时滞OMlB系统

针对由外部随机激励引起的电力系统随机功率波动：这些功率波动可以理解为由可再生能源发电产生，也可以理解为由电动汽车等负荷产生，一般情况下可以将其近似设为具有平稳独立增量的高斯过程［15］。因此在转子运动方程右侧加上随机激励项，式（4）改为：

式中W（t）——随机激励，表现形式为满足高斯分布的白噪声过程；σ0——随机激励强度。

将式（5）写成向量型式：

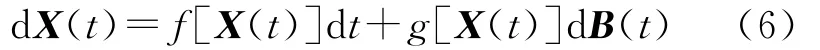
其中B（t）=［B1（t），B2（t），…，Bn（t）］T是n维维纳过程，初值X（t0）与B（t）独立，B（t）的形式导数为dB（t）／dt=W（t）；

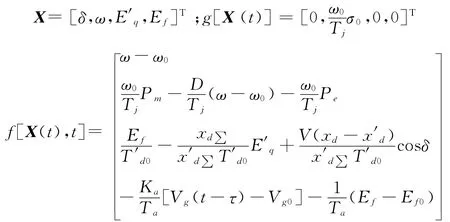
2.3 随机微分方程的数值计算方法

对于随机微分方程来说，只有满足一些特殊表达的简单系统才能够解析求解，更多的情况需通过数值计算方法获得解过程的轨迹。EM数值方法是随机微分方程最简单的数值求解的方法［16］。设随机过程X（t）是随机微分方程（6）的解过程，对于某个正整数N，记Δt=（T-t0）／N，τj=jΔt，Xj=X（τj），j=0，1，2，…，N，

则EM数值方法的差分迭代公式为：

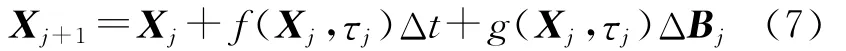
3 随机时滞OMlB系统仿真分析

算例系统如图1所示，本文在仿真计算时采用的参数设置为：Tj=10.0s，Xd=0.982pu，Xq=0.982pu，X′d=0.344pu，Xe=0.604pu，D=0.5，T′d0=5.0s，Vg0=1.05pu，Pm=0.45 pu，ω0=314.15rad／s，Ka=55，Ta=0.5s。

3.1 时滞对功角曲线的影响

时滞随机OMIB系统数学模型如式（5）所示，采用EM方法仿真获得功角响应曲线，仿真1000次并平均，根据平均功角曲线分析时滞对稳定性的影响。不同时滞下的功角曲线均值见图3～图5。

（1）σ0=0.01

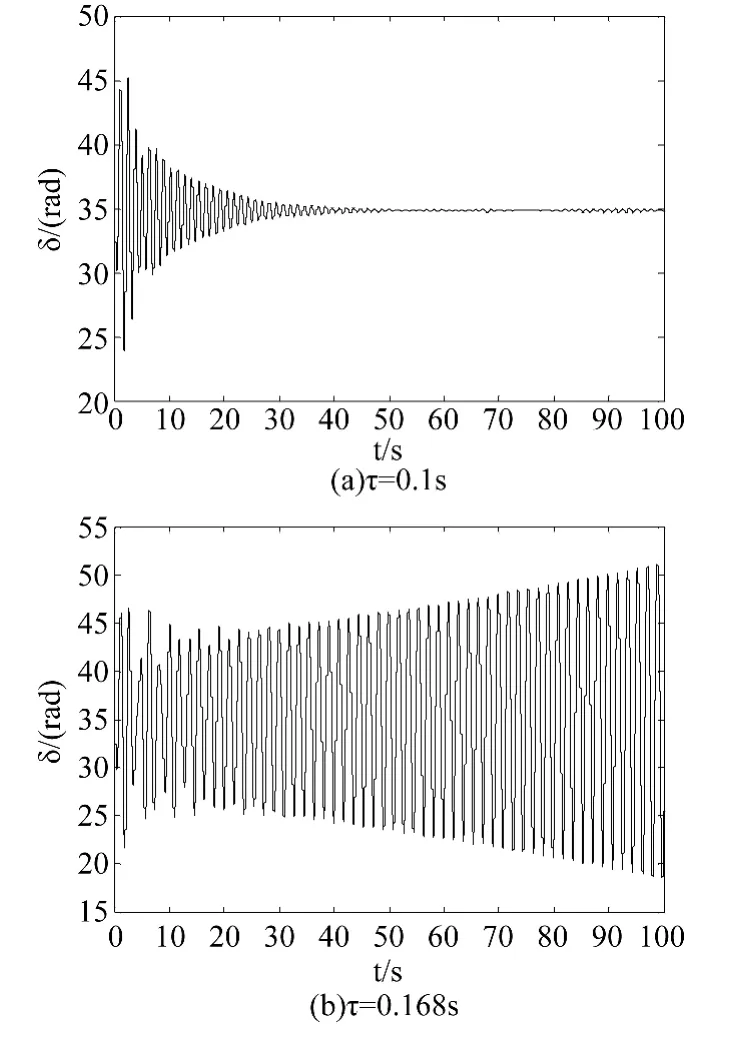
图3 σ0=0.01时均值功角曲线

（2）σ0=1

（3）σ0=1.2

从图3可以看出：当随机激励为高斯白噪声，且激励强度σ0=0.01时，时滞τ较小时系统稳定，但时滞大于0.167s时，系统出现增幅振荡并最终失稳。从图4可以看出：当激励强度增大至σ0=1时，时滞较小时或时滞较大时系统都可能失稳，但时滞适中（如当τ=0.16s）时系统反而稳定。图5可以发现：当激励强度增大至σ0=1.2时，无论时滞取值多少，系统都失稳。

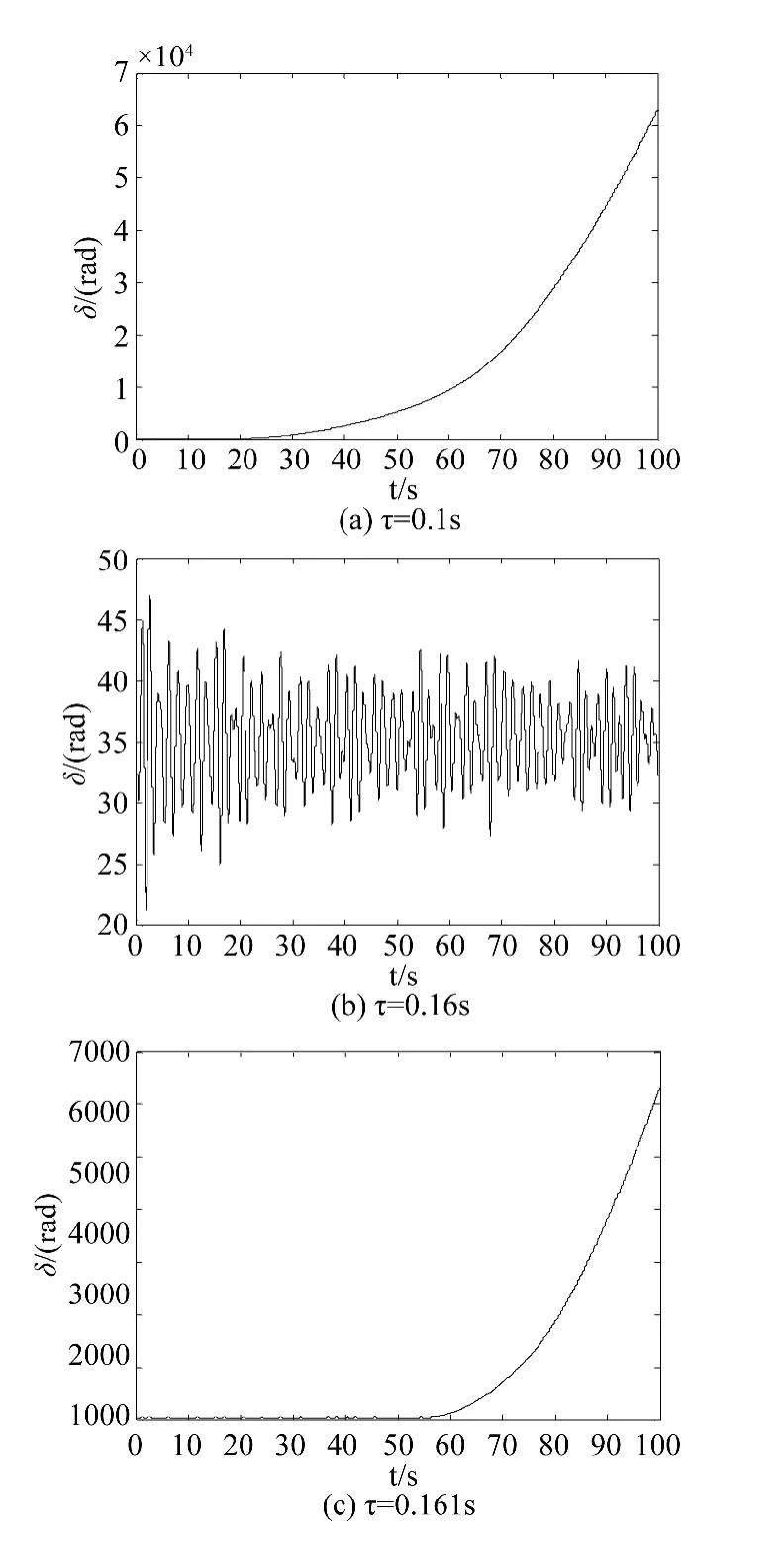
图4 σ0=1时均值功角曲线

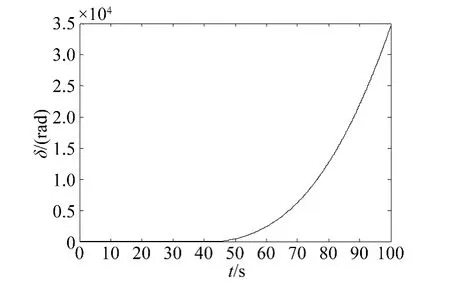
图5 σ0=1.2时均值功角曲线

表1给出了不同激励强度及时滞参数下的发电机功角曲线均值及稳定性判断。从表1可看出：

（1）随机时滞电力系统的稳定性不仅取决于激励的强度，还与时滞的大小密切有关。

（2）系统存在较小的时滞可能有利于系统的稳定性，但较大的时滞通常不利于系统的稳定性。

表1 不同时滞及激励强度下的功角稳定性

3.2 不同激励分布的影响

上述仿真分析了激励强度对时滞系统稳定性的影响，下面进一步分析当W（t）为不同分布的白噪声对系统稳定性的影响。表2和表3分别列出了W（t）为均匀分布U（a，b）（其中a，b为均匀分布的区间）以及泊松分布P（λ）（其中λ为泊松分布的均值和方差）下的系统稳定性仿真结果。

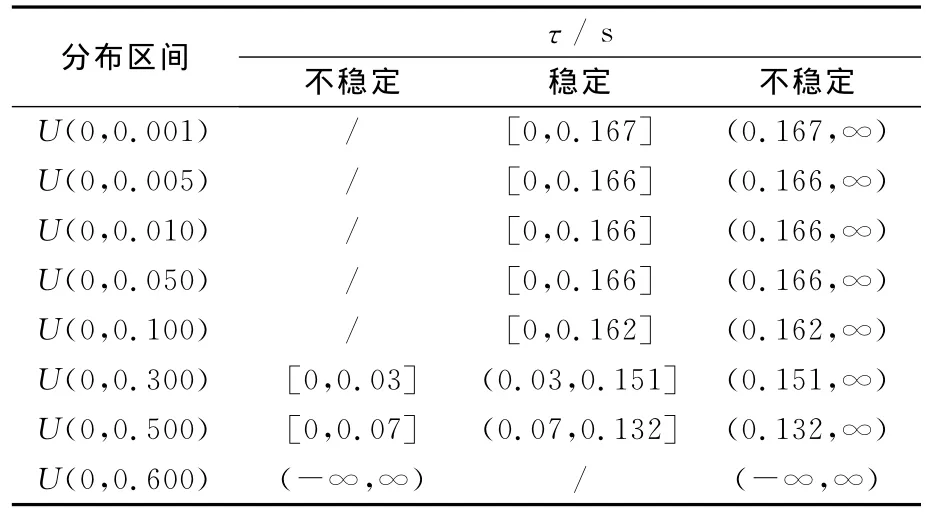
表2 均匀分布白噪声激励下的功角稳定性

表3 泊松分布白噪声激励下的功角稳定性

由表2～表3可得：不同的随机激励分布下时滞电力系统的稳定域不同。因此在研究时滞电力系统的稳定性问题时，有必要获得负荷随机扰动或可再生能源的随机波动模型。

4 基于Pade近似的时滞系统小扰动稳定性分析

4.1 纯时滞环节的Pade近似

在频域中纯时滞环节用e-sτ表示，其中τ表示时滞。为了能方便地分析系统的特性，在不会产生较大误差的情况下，有时用有理函数来近似e-sτ，其中Pade（这里记作P（s））近似是常用的一种方法，表示如下：

式中l，k，j——正整数；！——阶乘。

Pade近似随阶数l和k的变化而变化，l+k的值越大，近似就越精确。

表4分别给出了1～3阶（l=k）的P（s）表达式［7］。

表4 Pade表达式

用一阶Pade表达式P（s）逼近纯时滞环节，在复频域中可用传递函数框图变换（图6所示）来获取其状态空间模型：

图6 传递函数框图变换

相应的状态空间方程为：

式中x1——与时滞环节相关的中间变量。

同理，三阶Pade近似的状态空间方程可表示为：

式中x1～x3——中间变量。

将Pade近似的状态方程与系统其余部分的状态方程相结合，就能得到整个系统的状态空间表达式。

4.2 基于Pade近似的时滞电力系统小扰动稳定性

当纯时滞环节用一阶Pade表达式近似时，式（4）修改为：

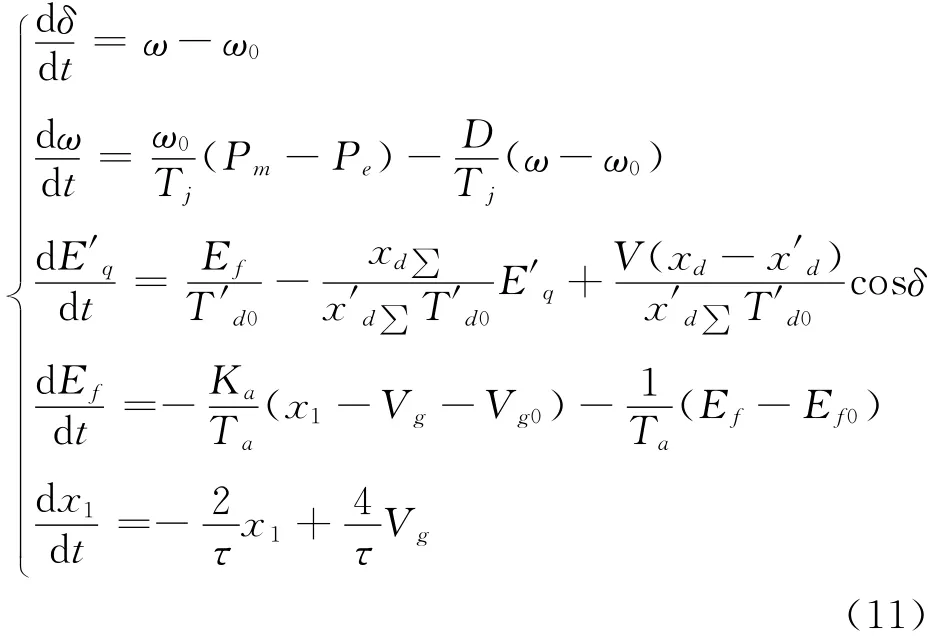
将动态方程（11）在平衡点处线性化，根据线性化后系统的状态矩阵求得含时滞OMIB系统的特征根，见表5。

表5 一阶Pade近似下的特征根

从表5可以看出：系统有两振荡模式以及一个衰减模式。随着τ的增加，振荡模式λ2，3的阻尼逐渐增加，但λ4，5的阻尼逐渐减小。当τ增加到0.173s时，λ4，5的实部大于零，系统不稳定。对照表1的仿真结果可以看出：在扰动强度较小σ0=0.001时，τ=0.167s时系统失稳，2者的结果基本一致。

进一步采用三阶Pade变换近似时滞环节。将式（10）代入方程（4）后，根据对应方程的线性化结果，求得不同时滞下的系统特征根，见表6。

由表6可以看出：采用三阶Pade近似时，τ=0.167s时系统处于临界稳定，τ=0.168s失稳。这与表1～表3仿真求得的临界稳定点0.167s吻合。

表63 阶Pade近似下系统特征值

4 结语

本文基于单机无穷大系统，建立了随机时滞电力系统的数学模型，仿真分析了不同随机扰动强度、不同随机激励分布、不同时滞下电力系统的动态特性。文中还将时滞环节用Pade表达式近似，分析了基于Pade近似的时滞系统特征根结果。

论文分析表明：在随机扰动强度较小时，基于高阶（三阶以上）Pade近似的时滞系统特征根结果与随机扰动下的系统稳定性吻合；但当扰动强度增大时，基于高阶（三阶以上）Pade近似的时滞系统特征根结果与随机扰动下的仿真结果有较大的差异。这是因为系统存在强非线性（时滞）环节，其原点稳定性的吸引域较小。

［1］ MORI T，KOKAME H.Stability of x·=Ax（t）+Bx（tτ）［J］.IEEE Trans on Automatic Control，1989，34（4）：460-462.

［2］ 胡海岩，王在华.非线性时滞动力系统的研究进展［J］.力学进展，1999，29（4）：501-512.HU Hai-yan.Review on nonlinear dynamic systems involving time delays［J］.Advances in Mechanics，1999，29（4）：501-512.

［3］ 贾宏杰，陈建华，余晓丹.时滞环节对电力系统小扰动稳定性的影响［J］.电力系统自动化，2006，30（5）：1-5.JIA Hong-jie，CHEN Jian-hua，YU Xiao-dan.Impact of time delay on power system small signal stability［J］.Automation of Electric Power Systems，2006，30（5）：5-8，17.

［4］ 贾宏杰，谢星星，余晓丹.考虑时滞影响的电力系统小扰动稳定域［J］.电力系统自动化，2006，30（21）：1-5.JIA Hong-jie，XIE Xing-xing，YU Xiao-dan.Power system small signal stability region with time delay considered［J］.Automation of Electric Power Systems，2006，30（21）：0-0.

［5］ WU H X，NI H，HEYDT G T.The impact of time delay on robust control design in power systems［J］.IEEE Power Engineering Society Winter Meeting，New York，USA，2002，2：1511-1516.

［6］ 袁野，程林，孙元章.考虑时延影响的互联电网区间阻尼控制［J］.电力系统自动化，2007，31（8）：12-15.YUAN Ye，CHENG Lin，SUN Yuan-zhang.Inter-area damping control of interconnected power systems considering the time delay of feedback signal［J］.Automation of Electric Power Systems，2007，31（8）：12-16.

［7］ 叶华，霍健，刘玉田.基于Pade近似的时滞电力系统特征值计算方法［J］.电力系统自动化，2013，37（7）：25-30.YE Hu，HUO Jian，LIU Yu-tian，et al.A method for computing eigenvalue of time-delayed power systems based on Pade approximation［J］.Automation of Electric Power Systems，2013，37（7）：25-30.

［8］ YUE D，HAN Q L.Delay-dependent exponential stability of stochastic systems with time-varying delay，nonlinearity，and Markovian switching［J］.IEEE Trans on Automation Control，2005，52（2）：217-222.

［9］ YUE D，WON S.Delay-dependent robust stability of stochastic systems with time delay and nonlinearity uncertainties［J］.IEE Electron Lett，2001，37（15）：992-993.

［10］ CHEN W H，GUAN Z H，LU X M.Delay-dependent exponential stability of uncertain stochastic systems with multiple delays：an LMI approach［J］.System＆Control，Lett，2005，54：547-555.

［11］ HUA M，DENG F，LIU X，et al.Robust delay-dependent exponential stability of uncertain stochastic system with time-varying delay［J］.Circuits Syst Signal Process，2010，29：519-526.

［12］ XU S Y，CHEN T.Robust H∞control for uncertain stochastic systems with state delay.IEEE Trans on Automatic Control，2002，47（12）：2089-2094.

［13］ 倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析［M］.北京：清华大学出版社，2002.

［14］ 何仰赞，温增银.电力系统分析（下册）［M］.武汉：华中科技大学出版社，2002.

［15］ 刘咏飞，鞠平，薛禹胜，等.随机激励下电力系统特性的计算分析［J］.电力系统自动化，2014，38（9）：137-142 LIU Yong-fei，JU Ping，XUE Yu-sheng，et al.Calculation analysis on power system characteristics under random excitation［J］.Automation of Electric Power Systems，2014，38（9）：137-142.

［16］ Hamdy M A.Euler-maruyama numerical solution of some stochastic functional differential equations［J］.Internation Journal of Applied Mathematics and Computation，2007，11（1）：13-30.