电力系统仿真计算中变电站等值模式研究

冯长有，刘力华，关 立，邱 威，刘 畅

（国家电力调度控制中心，北京 100031）

1 目前国内电网架构及运行调度面临的问题

实际电网中从发电厂到用户之间包含多个电压等级输电网络，比如我国华北—华中互联电网中共有1 000kV／500kV／220kV／110kV／35 kV／10kV等多个电压等级，各电压等级输电网间通过变压器实现电压变化和电能交互，并实现分层分区运行，尽量避免出现电磁环网运行方式［1］。实际运行中，750kV、500kV等高电压等级电网由于运行电压高、有功网损较小、传送功率较大，基本以环网形式运行，负责电能远距离输送；220kV、110kV等较低电压等级电网运行电压较低、网损较大，多呈现辐射状，负责对分片区域供电，对于大用户直接经过220kV、110kV供电，对于负荷较小用户比如居民用电、商业用电，再经过变压器转变为更低的35kV、10kV供电。电压等级高低是相对的，随着电网结构发展而变化，在80年代以前，我国主干电网为220kV环网，随着社会经济发展，逐渐不能满足用户需求，主干电网升级为500kV环网，220kV网架逐渐解环对单个分区供电。对于我国各大区域电网，目前除西北电网采用750kV／330kV／110kV网架结构外，其余区域基本形成了500kV／220kV／110kV输电网络，以500kV电压等级为主网架结构，每个500kV变电站带几回甚至十几回220 kV线路，负责一片区域的负荷供电或电源上网，典型变电站结构如图1所示。对于其中某500 kV变电站A，作为主网架中的一个节点，经过500kV三绕组主变带220kV辐射性电网，包含2路220kV负荷出线，1路220kV机组并网线路，经过1台220kV变压器带4回110kV负荷线路和1回110kV机组并网线路。

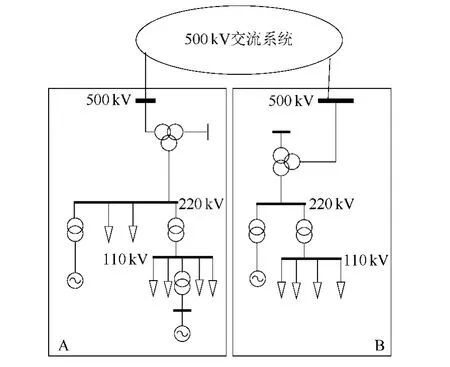
图1 实际电网中变电站接线图

随着我国特高压输电工程的全面推进，电网进入了特大型交直流混联电网新时期，电网特征、运行特性都发生了重大变化，相互耦合程度越来越深。对于呈现非线性、动态变化的复杂网络，仅仅依靠调度运行人员经验已不足以掌控，调度机构必须进行深入的分析校核，根据校核结论确保电网经济、安全运行［2］。从校核时间尺度来说，分为年度、月度、日前和实时校核，其中年度、月度校核属于运行方式专业工作范畴，日前校核属于调度计划专业工作范畴，实时分析（也称为在线安全稳定分析）属于调度运行专业工作范畴［3，4］；从校核内容来说，分为静态安全分析、暂态稳定分析、短路电流计算、电压稳定分析及小扰动动态稳定分析等［5］。在进行分析计算时，并不是对电网中所有设备进行建模，而是根据电网实际情况对主网架进行简化，主要就是对其中变电站进行等值，然后对等值电网进行计算分析，根据分析结论给出电网运行特性、制定稳控装置执行策略和运行控制措施，调度运行人员根据相应措施调控电网和处置事故［6］。

在对实际电网进行分析校核时，如何确定合适的网架简化策略就成为调度运行部门首要考虑的问题，其中主要就是变电站等值模型，建模精度直接决定了仿真分析结果与实际运行特性的接近程度。建模过粗则仿真结果不能反映电网实际特性，所给控制策略可能过于保守甚至错误，策略保守导致电网运行不经济，而策略错误则为电网运行带来隐患，发生故障时可能产生连锁反应导致垮网；建模过细则仿真模型中设备较多，一方面需要大量人员开展模型参数实测，进行模型参数维护，另一方面可能导致潮流调整困难甚至不收敛，无法给出实际控制措施。目前已有文献主要集中在设备自身建模精度分析上［7-10］，尚未有从系统仿真计算角度对变电站等值建模进行详细讨论。

基于此，本文结合实际电网仿真计算情况，给出了两种变电站等值模式，重点从暂态稳定、短路电流、小扰动动态稳定、电压稳定等角度，分析了两种模式下的电网仿真结果差异，利用PSASP软件进行了验证，并给出了相应的等值建议。

2 变电站等值模式

在对主网架进行简化等值时，主要对低电压等级网架结构等值，也就是对环网中的变电站进行等值。目前仿真分析中，根据负荷和机组等效位置不同，考虑是否包括变电站低电压主变压器，如图1中变电站A是否包括220kV变压器，可分为如下两种等值模式。

2.1 等值模式一

该等值模式包含低电压主变压器，对于低电压等级带负荷线路合并为等效负荷，挂在主变压器上；对于并网机组不予等值，直接挂在变压器上，原则如下：（1）对于站内仅带负荷的低电压等级线路，将负荷归并后采用统一负荷模型进行处理，直接等值在主变出线处，线路功率作为等效负荷功率；（2）对于所带负荷有功为负的线路，说明该线路所带区域中含有机组且出力大于实际负荷，将其等效为机组，动态模型及参数根据所带机组确定或采用典型值；（3）对于带有电源的低电压线路不进行等值。

该等值模式下，将不会出现负负荷情况，大幅度降低了仿真模型中负负荷数量，但建模量增加较多，潮流调整也更为复杂。根据该等值模式，对图1所示变电站A、B，110kV侧3个带负荷线路直接等值为负荷，1个所带负荷为负值线路等值为机组且动态参数采用典型参数，对于重要110 kV电源仍然保留，等值后如图2所示。

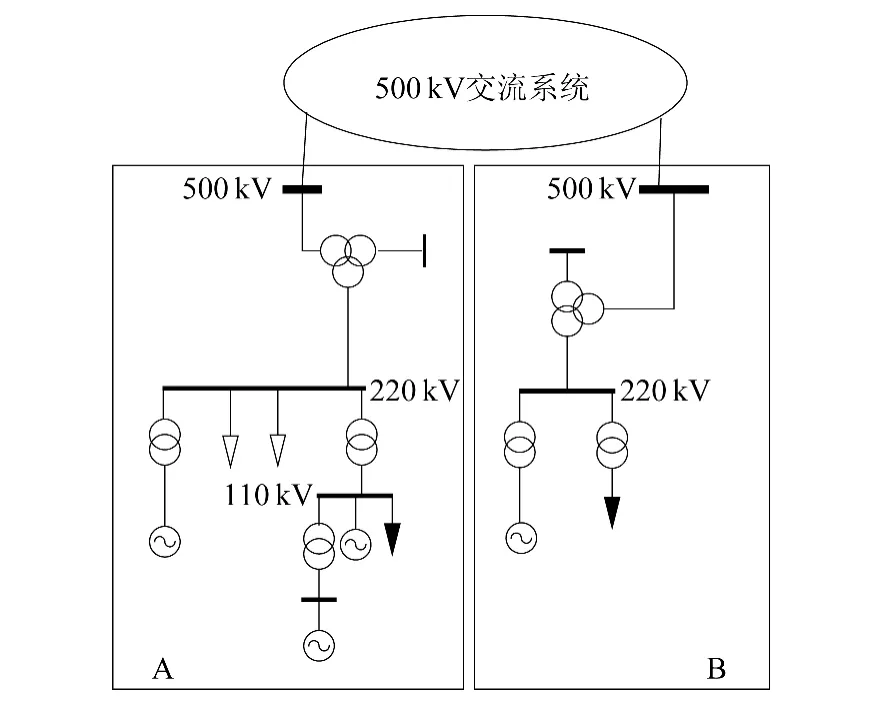
图2 等值模式一下变电站接线图

2.2 等值模式二

该等值模式不包含低电压主变压器，将站内低电压等级线路所带负荷和机组等效后，直接等效至高压侧，等值原则为：（1）负荷建模至主变压器高压侧，去除变电站变压器及其附属的补偿器和相连的低电压等级支路，将变压器高压侧绕组的功率作为等值负荷功率；（2）去除低电压等级线路中所连发电机和相应的厂用负荷及近区线路，其对应主变上网点等值负荷功率为负值，模型为恒阻抗。

该等值模式下，变电站中低电压等级线路均被等值，低电压变压器被等效为等值负荷，若等值负荷值为正，则说明经等值前该变电站中低电压变压器所带负荷高于机组出力，若等值负荷为负，则说明等值前所带机组出力高于负荷，将机组按负负荷处理，忽略其动态特性，当机组数量较多时，必然影响动态仿真结果。该等值模式下，对于图1所示变电站A、B，等值后如图3所示。

图3 等值模式二下变电站示意图

以上两种等值模式既可应用于局部电网，也可应用于全网；既可应用运行方式专业的离线方式计算，也可应用于调度运行专业的在线稳定分析计算。等值模式二是在等值模式一基础上进行了简化，仅保留了主干网架部分，网架结构更加清晰、潮流调整更为方便，但由于等值可能会导致电网特性发生较大变化，当低电压等级中含有较多机组时，导致仿真结果不能准确反映实际情况，下面将从理论和实际仿真角度加以验证。

3 两种变电站等值模式下仿真分析

上述两种变电站等值模式本质上都是对负荷或机组进行整合，只是等值深度有所不同，等值前后负荷功率、电压未发生大的变化，主网及连接在主网中机组状态未改变，因此对于主网潮流计算和静态安全分析（N-1）来说，计算结果基本相同，表1给出了实际电网中某条线路开断后，其近区其余两回线路的潮流水平，两者基本相同。

表1 两种等值模式下静态安全分析结果

两种等值模式对接在低电压等级线路上机组处置不同，对于暂态稳定、小扰动动态稳定、短路电流计算、电压稳定等动态计算有较大影响，下面主要从这些方面进行分析。

3.1 暂态稳定分析

负荷等值或机组等值带来大量静态参数和动态性能变化［12］，从不同方面影响扰动过程，对稳定分析结果影响也各不相同，甚至相互对立；同一变化在不同故障下对稳定分析结果影响可能完全相反。

3.1.1 负荷等值

（1）单个变电站

仅对其中单个变电站采用模式二等值，其余变电站采用模式一。负荷模型通常由异步电动机和恒阻抗混合构成，在电网中突然短路后异步电机供给电流的衰减时间常数为百分之几秒，在等值后负荷异步电机供给电流虽略有增加，但在大电网中没有产生显著影响。故障切除后，异步电机内电势已降至0，必须重新建立电压；等值前后电动机暂态时间常数相同，建立起端电压速度在不考虑外电路影响时完全相同。但由于不同等值模式下负荷上网支路阻抗水平不同，因未对主变建模，等值模式二上网阻抗明显小于模式一，电压降减小，导致电压恢复速度下降，使得母线短路动态稳定性下降。离等值负荷电气距离越远，受到影响越小，大扰动动态稳定性下降越少。

以某变电站为例，该变电站所带均为负荷，分别对该变电站采用等值方式一、等值方式二进行负荷等值。考虑该变电站所带某220kV出线故障后，近区母线电压恢复情况，故障时间为1.0s、故障类别为三相、故障切除时间为1.12s。表2给出了故障切除后近区母线电压变化（标幺值），可以看出模式二下负荷母线故障后电压恢复速度变缓，降低了动态稳定性。

表2 两种等值模式下母线电压变化过程

（2）多个变电站

1）多个变电站负荷等值后，动态仿真使用的网络方程中各支路阻抗和注入电流的变化呈分散性。动态仿真使用的网络方程，由原电网方程消去没有连接动态元件的节点形成，即星网变换［11］。对n个节点的星形电网，假设1号节点为中心点，2号节点为负荷等值点。

由星网变换规则，消去1号节点后有：

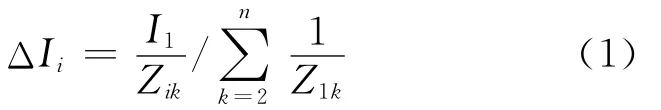
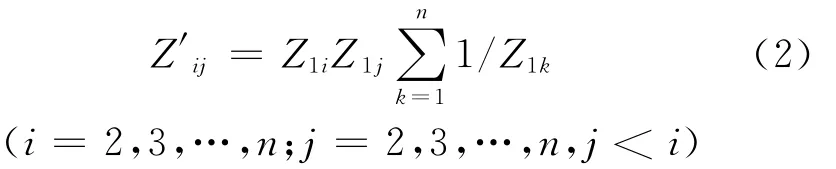
式中Ii——i号节点注入电流；Z1i为i号节点的支路阻抗；ΔIi为电流I1消去分散移置后在i号节点出现的电流增量；Z′ij——星网变换后各节点之间的阻抗。

将2号节点负荷等值，意味着Z12减小，I2增大。对星网变换后的支路电流和网络阻抗的影响是：ΔI2增大，ΔI3、…ΔIi、…ΔIn减小；（j=3、…n）减小，（i=3、…n，j=3、…n，j＞i）增大。由此可见单个负荷等值后的网形电路部分节点注入电流增大，部分节点注入电流减少；部分支路阻抗增加，部分阻抗减小。当需要等值负荷在电网中大量、分散分布，消元后的网络方程中注入电流和阻抗的变化呈现强烈的分散性。

2）等值后阻抗和注入电流变化的分散性导致仿真法动态稳定分析结果没有统一规律。电网阻抗减小将导致故障冲击变大，振荡平息变快。若故障点靠近电源，则前者对稳定影响更大，若靠近负荷，则后者对稳定影响更大。负荷节点注入功率增大，在故障初始瞬间能提供更多电流支撑电压，在母线电压降低时需要吸收更多的无功。由此可见，即使确切的阻抗和注入功率的变化对大扰动稳定性的影响也需要结合故障和电网的具体情况分析。等值后阻抗和注入电流变化分散性，无法给出统一变化规律。

3.1.2 发电机等值

模式二将机组等值成了负功率的恒阻抗负荷，模式一保留了重要机组，两者对大扰动故障分析的影响与故障点距机群的电气距离等电网状况有关，主要体现在：

（1）模式二去除了发电机动态特性

故障点离110kV发电机群电气距离非常近时，短路持续期间这些机组电磁功率接近于0，发电机在不平衡功率作用下发生剧烈的摇摆，故障切除后在惯性作用下功角持续振荡，输出功率仍大幅波动，成为新的扰动源。等值成无动态特性的负荷在故障前后阻抗恒定，输出功率随端电压变化，使大扰动稳定性增强。图4给出了两种等值模式下，实际电网故障后某线路有功波动情况。

图4 两种等值模式下暂态稳定计算情况

（2）模式二去除机组电压、功率调节能力

随故障点离110kV发电机群电气距离增加，短路过程中这些发电机机端的不平衡功率减小，故障切除后功角振荡平息加快，发电机附属的励磁调节器对电压的调节作用、调速器对频率的调节作用更早得到体现，帮助电网尽快恢复稳定。当电气距离增大到超过某值，110kV机组调节能力对动态稳定性的积极作用超过摇摆振荡带来的负面影响，等值成负荷后大扰动动态稳定性下降。分界点与电网规模、拓扑结构、动态参数均有关，很难给出明确的界定。

（3）模式二去除了潜在的危险振荡模式

110kV机组转子惯性时间常数小，阻抗大，容易与其它地区的机群形成区域间振荡模式。这种振荡模式通常频率低、阻尼弱。当故障点与110kV机群的电气距离超过某值，使该机群各机组在扰动过程中能保持接近同调，加上故障后电网结构变弱，该模式容易被激发，引起周期性摆动失稳。110kV机组等值成恒阻抗负荷，消除了潜在振荡模态，提高了故障动态稳定性。

暂态稳定分析过程中以上三种影响同时存在，随故障和电网状况不同，起主导作用的影响因素也不相同。

3.2 短路电流分析

在实际计算中，通常采用简易短路电流计算方法，即不考虑负荷影响，只考虑电源和网架结构，也就是基于方案（网架）的计算方法［13］。对于等值模式一短路示意图如图5所示，电网对地支路主要为线路对地电容、无功补偿元件，总体上表现为较大的容性电抗。VS为等值电压源，XLi（i=0、1、…4）为等值电抗，XCi（i=1、2、3）为等值电容，其中XL3代表电网末端220kV变压器，XC3代表接于该变压器低压侧的补偿电容。

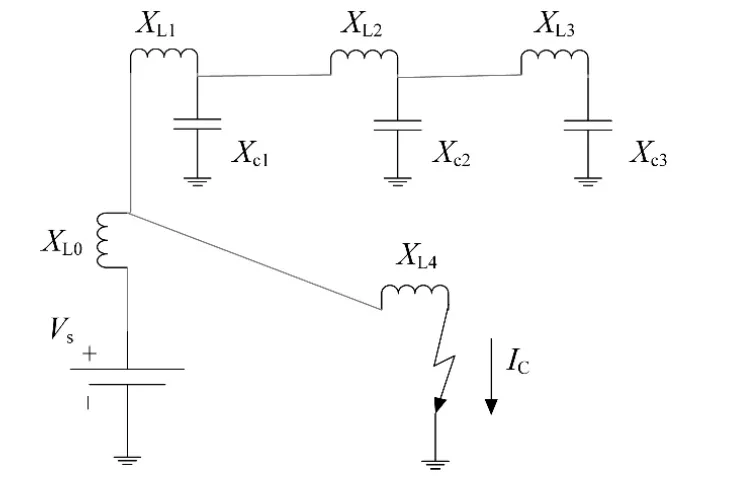
图5 基于方案的短路电流计算示意图

短路电流IC可计算为：

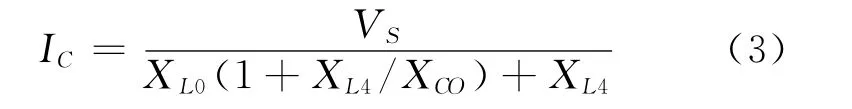
等值模式二下，由于主变压器及附属补偿装置被等值成负荷后，根据方案方式短路电流计算规则，负荷必须去除，相当于图5中XL3和XC3的支路被移除。则XCO变为：

220kV变压器所接入电容器组的容抗通常大于变压器高低压侧间的电抗，因而XL3+XC3呈容性，小于0。对比式（4）和式（5），知负荷等值后集中电抗XCO变小。同时由于低电压等级中电源也被等值，减少了短路电流来源，降低了短路电流水平。

上述两种因素下，导致模式二基于方案的短路电流结果总是低于模式一，计算结果偏乐观。表3为实际电网中两种模式下短路电流计算结果。

表3 两种等值模式下短路电流计算结果

3.3 小扰动动态稳定分析

对于两种等值模式，等值前后负荷功率、电压和上网阻抗变化较小，主网架及接入主网的发电机、直流输电系统、可控串补等动态元件及其调节元件的状态并未发生变化，因此涉及主网的振荡模态和机组参与程度不会发生大的变化，与负荷相关的振荡分量在各负荷间重新分布，总体上对小干扰计算结果影响较小。模式二下，由于部分接入低电压等级的机组被等值，与这些机组强相关的振荡模式消失，这些机组参与的其它振荡模态则由于参与机组减少，振荡频率、阻尼比、机组参与因子都有一定程度改变。

表4给出了两种等值模式下基于实际电网的小扰动动态稳定分析计算结果，可以看到模式二下部分振荡模式消失，其他振荡模式的频率、阻尼比略有变化。

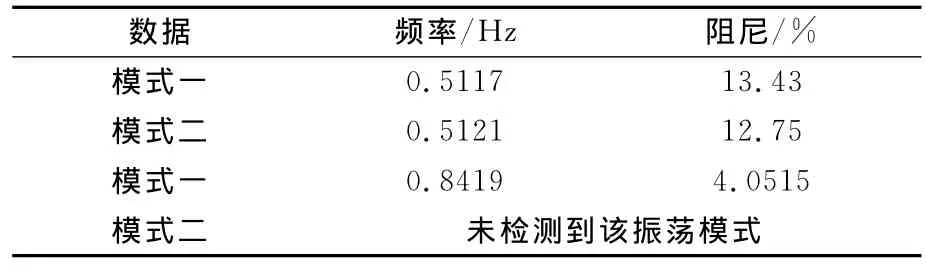
表4 两种等值模式下小扰动动态稳定分析结果

3.4 电压稳定

相比于等值模式一，模式二将变电站的220 kV变压器及其附属的补偿器和相连的110kV支路进行了等值，降低了与主网阻抗值，电气距离减小、损耗降低，电压稳定裕度必然偏大，计算结果偏乐观。表5给出了两种等值模式下，基于全网负荷-发电增长模式下，某变电站电压稳定计算结果。

表5 两种等值模式下电压稳定分析结果

3.5 对等值模式选择的建议

（1）针对不同电源结构电网在进行方式研究时，所采取的等值模式应不同。对于经低电压等级并网机组较多地区，如水电较多的四川、湖北、湖南、福建等地区电网，建议采用模式一等值；对于机组主要接入高电压等级且以负荷为主电网，如江苏、山东、浙江电网，建议采用模式二等值。

（2）对于同一个交流同步电网在进行不同需求的分析计算时，所采取的等值模型也不同。对于进行跨区域跨省方式校核时，关注点为区域及省间断面的稳定情况，建议采用模式二，对于省内或地区内方式校核，主要关注小区域内电网运行情况，建议在其他区域采用模式二等值的前提下，本地区采用更详细的模式一等值。

在实际电网仿真中，为既反应实际电网运行特性又尽可能减少工作量，采取两种等值模式共存模式，比如对华北华中同步电网，建议四川、湖南、湖北等水电较多地区及蒙西、河北等风电较多地区，采用模式一等值。

［1］ 刘振亚.特高压交直流电网［M］.北京：中国电力出版社.2013.

［2］ 曾鸣，李娜，董军，等.基于大安全观的电网运行管理关键技术［J］.电力系统自动化，2012，36（16）：9-13.ZENG Ming，LI Na，DONG Jun，et al.Key technologies of power grid operation and management based on philosophy of general security a view of blackout in India［J］.Automation of Electric Power Systems，2012，36（16）：9-13.

［3］ 王锡凡，王秀丽，陈皓勇.电力市场基础［M］.西安：西安交通大学出版社，2003.

［4］ 张伯明，吴素农，蔡斌，等.电网控制中心安全预警和决策支持（ESWC）系统设计［J］.电力系统自动化，2006，30（6）：1-5.ZHANG Bo-ming，WU Su-nong，CAI Bin，et al.Design of an early warning and security countermeasure system for electric power control centers［J］.Automation of E-lectric Power Systems，2006，30（6）：1-5.

［5］ DL 755-2001.电力系统安全稳定导则［M］.北京：中国电力出版社，2001.

［6］ 刘友波，胡斌，刘俊勇，等.电力系统连锁故障分析理论及应用［J］.电力系统保护与控制，2013，41（9）：148-155.LIU You-bo，HU Bin，LIU Jun-yong，et al.Power system cascading failure analysis theories and applicationⅠ-related theories and applications［J］.Power System Protection and Control，2013，41（9）：148-155.

［7］ Huang Z Y，Kosterev M，Guttromson R.Model Validation with Hybrid Dynamic Simulation［J］.Proceedings of IEEE Power Engineering Society General Meeting 2006，Montreal，Canada，2006.

［8］ 周成，贺仁睦.电力系统仿真模型有效性的动态评估［J］.电网技术，2010，34（3）：61-64.ZHOU Cheng，HE Ren-mu.Dynamic evaluation of effectiveness of power system simulation models［J］.Power System Technology，2010，34（3）：61-64.

［9］ 贺仁睦.电力系统动态仿真准确度的探究［J］.电网技术，2000，24（12）：1-4.HE Ren-mu.Research into veracity of power system dynamic simulation［J］.Power System Technology，2000，24（12）：1-4.

［10］ 沈沉，黄少伟，陈颖.未来电网的快速建模与仿真方法初探［J］.电力系统自动化，2011，35（10）：8-16.SHEN Chen，HUANG Shao-wei，CHEN Ying.Primary studies on fast simulation and modeling for future power systems［J］.Automation of Electric Power Systems，2011，35（10）：8-15.

［11］ 王锡凡，万方良，杜正春.现代电力系统分析［M］.北京：科学出版社，2003.

［12］ 汪小明，刘涤尘，吴军，等.电力系统暂态稳定分析广义负荷模型［J］.电网技术，2011，35（3）：44-48.WANG Xiao-ming，LIU Di-chen，WU Jun，et al.A generalized load model for transient stability analysis of power system［J］.Power System Technology，2011，35（3）：44-48.

［13］ 刘文颖，但扬清，朱艳伟，等.基于电力系统分析综合程序的限流方案综合评价方法［J］.电网技术，2011，35（8）：150-154.LIU Wen-ying，DAN Yang-qing，ZHU Yan-wei，et al.A power system analysis software package based comprehensive evaluation method for short-circuit current limitation strategy［J］.Power System Technology，2011，35（8）：150-154.