一元表征视角下几个数学问题的教学设计

（长江工程职业技术学院，武汉 430212）

高等数学的学习总是要从一元过渡到多元的，我们的思维也要从一维过渡到多维。如何拓展学生的数学发展能力，如何延续学生的数学学习能力？如何让高职高专有关专业学生也能学好相应专业需要的较高深的数学知识，在教学实践中应高度注意数学公式，数学法则，亦或数学技巧的统一性与传承性。高等数学微积分是理工科学生的基础课也是必修课，无论哪个层次的理工科学生只要掌握了微积分的核心知识“导数公式及求导法则”，他就可以在各有关数学知识间穿越了，甚或可以感叹“还是那么些公式，还是那么些法则，还是那么些技巧”。在一些理工科或高职高专的课程中，要从实平面（空间）过渡到复平面（空间），把实和虚有机地结合与统一起来。

1 空间和发展

数学教学要特别注重逻辑和理论，要充分发挥推导和证明的作用，更要注意教学对象，也要注意当下人们处理事情（学习）的快节奏。指导学生要化繁为简，少些理论的讨论，可以点带面，举一反三，以发展为线索。懂了记住了会用了就是硬道理。

拿空间来说有一维空间，二维空间，三维空间。就距离而言有一维空间距离，二维空间距离，三维空间距离，一维空间（数轴）两点间的距离有公式：d=|x2-x1|，从统一的角度和发展记忆的角度把它改写为下面的形式：。

学生在高中阶段学习和研究过二维空间（平面上）两点的距离且有公式：。

学生在多元函数的学习中要体会一元和多元，空间要从一维，二维发展到三维，要从现实空间发展到理论上的多（N）维。

猜测也好，类比也好，发展也好，可推知空间二点A（x1，y1，z1），B（x2，y2，z2）间的距离，进一步推知在N维空间数学就定义X=（x1，x2，…，xi，…，xn），Y=（y1，y2，…，yi，…，yn）两点的距离（范数）

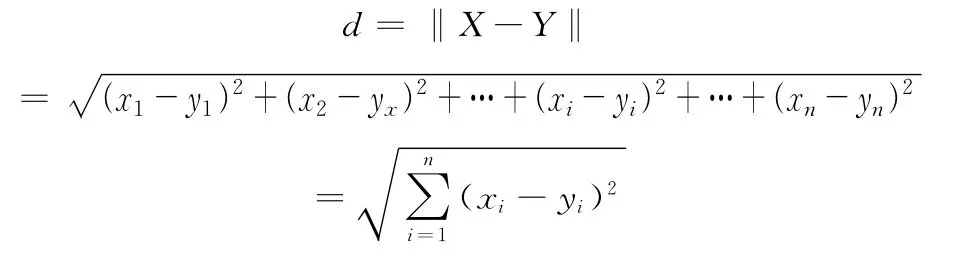
2 解的联系、解的结论

事物的发展总是由简单到复杂，由特殊到一般，由个体到群体。一篇文章如果用了比拟，用了联想，文章定能增色不少。数学的研究也好，学习也好，如果也用比拟，也用联想，那么也许可化复杂为简单，可使不同的数学内容有整体感，特别是可使当下众多的高职高专的数学学习者印象深刻，记忆长久。

不妨来看一看这个方程：ax=b。有人说它太平凡，太简单，不值得我们去研究，其实不然。

如果从启发学生，增强教学效果方面看，此方程有十分丰富的内涵。

（2）a=0，b≠0，ax=b，方程矛盾，无解。

（3）a=b=0，ax=b，方程总成立，无数解，x∈R

进入到工程数学的内容中，也要讨论方程组的解问题。线性方程组的解也是这样的三个方面的结论。

（1）：R（A）=R（）=R（AB）=n，方程组唯一解；且形式上有强的对比性ax=b⇒x=a-1b（a≠0）；AX=B⇒X=A-1B（|A|≠0）

（2）：R（A）=R（）=R（AB）＜n，方程组无数解；

（3）：R（A）≠R（）=R（AB）=n；方程无解。

进一步我们发展出各种解线性方程组的方法。例如，当|A|≠0，方程有简单的解的表达式：X=A-1B，故从这里出发，我们去讨论矩阵的运算，矩阵的求逆等等。

3 公式；法则；技巧的统一性

从法则上看，复变函数与积分变换中用于复函数的求导法则还是高数微积分中的法则：

尽管从函数的形态上看，复函数比同名称的函数要复杂好多，比如

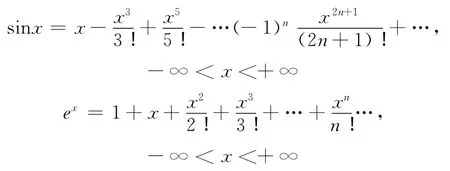
而在复变函数与积变换中又有多大的变化呢？

请对比一下：

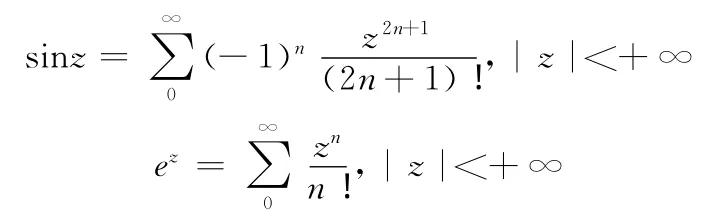
还是以复变函数与积分变换中一些问题的讨论来看看高数的延展性与数学的统一性吧。在高数中用洛必塔法则处理诸如型极限，在复变中对奇点分类时，也可借用洛必塔法则得到要的一些结果。如z=0，是这些函数的奇点而且是可去奇点。因为

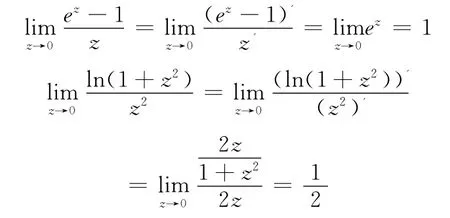
4 简化形式、注重内容、着重发展

现代科学研究告诉人们，在进行学习思考或研究时，运用的结果往往是在各种不同知识间不断转化，这就需要在短时间内开启学生的智慧，使之能自觉地学习，自主讨论，自如地运用经验和知识的储存，在新知识新课程面前信心满满。

在进行复杂的高阶行列式的讨论时，面对学生要遵循简单简化发展的原则进行课堂设计。在形式上有二、三阶、高阶行列式

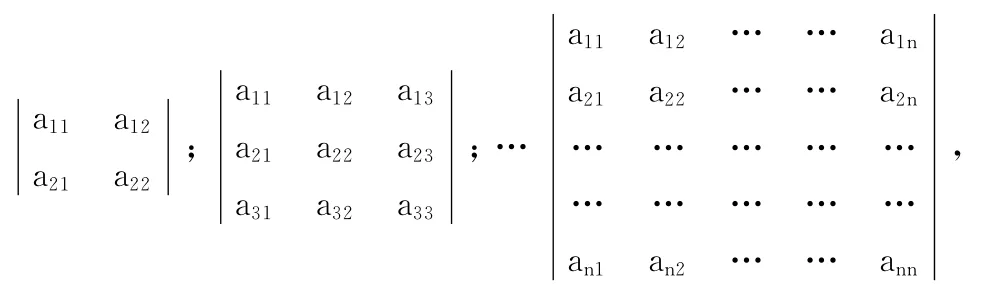
将它们简化为内容丰富多彩的形态|A|2×2；|A|3×3；|A|n×n；|aij|。要让学生精于行列式的计算则要花点时间着重从二阶行列式性质发展到行列式性质，让学生知道二阶的性质就是高阶的性质。故而，建议有关教材上把“二阶行列式性质”名称改为“行列式性质。

总之，今天学生队伍变化了，教学方法、手段也要变化。要在信息化时代这个大环境下做一个好的数学教师，要在数学的海洋中摄取即时的学生需要的知识教给学生。